北京信息科技大学：理学院各专业课程教学大纲汇编.pdf_大学文库

I 目录信息与计算科学专业《数学分析(1)(2)(3)》...................................................................................................................1 《高等代数与解析几何(1)(2)》................................................................................................... 6 《大学物理 A(1)(2)》..................................................................................................................10 《物理实验 A(1)(2)》..................................................................................................................10 《专业认识与实践》...................................................................................................................10 《离散数学》...............................................................................................................................12 《常微分方程》...........................................................................................................................15 《概率论与数理统计》...............................................................................................................18 《数据结构》...............................................................................................................................22 《复变函数与积分变换》...........................................................................................................25 《数据结构课程设计》...............................................................................................................29 《运筹学与优化》.......................................................................................................................32 《数值分析》...............................................................................................................................35 《数学物理方程》.......................................................................................................................38 《数据挖掘》...............................................................................................................................40 《计算机网络设计与开发》.......................................................................................................43 《数学建模与数学实验》...........................................................................................................46 《微分方程数值解》...................................................................................................................49 《信息论基础》...........................................................................................................................51 《实变函数》...............................................................................................................................55 《数字信号处理》.......................................................................................................................58 《回归分析》...............................................................................................................................63 《多元统计分析》.......................................................................................................................66 《数学建模与数学实验课程设计》...........................................................................................69 《回归分析课程设计》...............................................................................................................71 《泛函分析》...............................................................................................................................74 《数值代数》...............................................................................................................................76 《算法分析设计》.......................................................................................................................79 《信息安全技术》.......................................................................................................................81 《精算数学》...............................................................................................................................85 《统计学课程综合实践》...........................................................................................................87 《毕业设计》...............................................................................................................................89 电子信息科学与技术专业《高等数学 A(1)(2)》(普通教学班)...........................................................................................93 《高等数学 A(1)(2)》(强化教学班)...........................................................................................93 《线性代数 A》........................................................................................................................... 93

II 《专业概论》...............................................................................................................................94 《概率论与数理统计 B》........................................................................................................... 97 《大学物理 A(1)(2)》..................................................................................................................97 《物理实验 A(1)(2)》..................................................................................................................97 《复变函数与积分变换 A》.......................................................................................................98 《数据结构》...............................................................................................................................98 《单片机原理与应用》.............................................................................................................102 《印刷电路板设计》.................................................................................................................104 《计算机组成原理与接口》.....................................................................................................107 《信号与系统》......................................................................................................................... 111 《半导体物理》......................................................................................................................... 115 《半导体器件》......................................................................................................................... 119 《嵌入式操作系统》.................................................................................................................122 《传感器原理与应用》.............................................................................................................126 《FPGA 设计及应用》..............................................................................................................130 《传感器原理及应用》.............................................................................................................134 《FPGA 设计及应用课程设计》............................................................................................. 136 《专业认识实践》.....................................................................................................................139 《专业英语》.............................................................................................................................141 《电子竞赛实训》.....................................................................................................................144 《数字信号处理》.....................................................................................................................146 《嵌入式系统及应用》.............................................................................................................151 《集成电路设计》.....................................................................................................................154 《智能平台应用开发》.............................................................................................................160 《IC 芯片及应用》....................................................................................................................167 《集成电路工艺与测试》.........................................................................................................171 《集成电路 EDA》....................................................................................................................176 《嵌入式软件设计》.................................................................................................................179 《物联网技术》.........................................................................................................................182 《硬件电路综合课程设计(基于单片机)》..............................................................................185 《信号系统与数字信号处理综合课程设计》........................................................................ 187 《专业实习》.............................................................................................................................190 《创新能力训练》.....................................................................................................................193 《集成电路综合课程设计》.....................................................................................................196 《智能信息系统应用综合课程设计》.....................................................................................200 《集成电路版图设计》.............................................................................................................202 《智能信息系统安全》.............................................................................................................206 《单片机进阶》.........................................................................................................................210

III 《DSP 技术及其应用》............................................................................................................ 213 《计算机网络》.........................................................................................................................217 《毕业设计》.............................................................................................................................220 应用统计学专业《数学分析(1)(2)(3)》...............................................................................................................223 《高等代数与解析几何(1)(2)》............................................................................................... 223 《大学物理 B》......................................................................................................................... 223 《常微分方程》.........................................................................................................................224 《概率论》.................................................................................................................................224 《专业认识与实践》.................................................................................................................227 《EXCEL》................................................................................................................................ 229 《矩阵论》.................................................................................................................................231 《数理统计》.............................................................................................................................233 《回归分析》.............................................................................................................................236 《多元统计分析》.....................................................................................................................239 《多元统计分析课程设计》.....................................................................................................243 《回归分析课程设计》.............................................................................................................245 《R 语言》................................................................................................................................. 248 《描述统计》.............................................................................................................................250 《数据结构》.............................................................................................................................252 《非参数统计》.........................................................................................................................257 《时间序列分析》.....................................................................................................................260 《运筹与优化》.........................................................................................................................263 《统计分析软件》.....................................................................................................................266 《应用随机过程》.....................................................................................................................268 《试验设计》.............................................................................................................................271 《数据挖掘》.............................................................................................................................274 《统计方法应用》.....................................................................................................................277 《时间序列分析课程设计》.....................................................................................................280 《数据挖掘课程设计》.............................................................................................................282 《科技英语》.............................................................................................................................284 《抽样调查》.............................................................................................................................286 《统计计算》.............................................................................................................................289 《保险精算学》.........................................................................................................................292 《专业英语》.............................................................................................................................294 《文本数据分析与推荐系统》.................................................................................................298 《抽样调查课程设计》.............................................................................................................302 《保险精算课程设计》.............................................................................................................304

IV 《统计计算课程设计》.............................................................................................................305 《运筹与优化课程设计》.........................................................................................................308 《组合数学》............................................................................................................................. 311 《计量经济学》.........................................................................................................................313 《风险理论》.............................................................................................................................316 《金融学》.................................................................................................................................319 《金融数学》.............................................................................................................................321 《数学建模与数学实验》.........................................................................................................325 《统计质量控制》.....................................................................................................................328 《国民经济统计学》.................................................................................................................331 《专业实习》.............................................................................................................................334 《离散数学》.............................................................................................................................337 《可靠性统计》.........................................................................................................................340 《贝叶斯统计》.........................................................................................................................342 《生物统计》.............................................................................................................................345 《市场调查与分析》.................................................................................................................348 《保险学原理》.........................................................................................................................350 《人口数学》.............................................................................................................................353 《科技讲座》.............................................................................................................................356 《描述统计课程设计》.............................................................................................................358 《应用统计课程设计》.............................................................................................................360 《毕业设计》.............................................................................................................................362 数理实验班《数学分析(1)(2)》....................................................................................................................365 《高等代数与解析几何(1)》.................................................................................................... 369 《高等代数与解析几何(2)》.................................................................................................... 372 《大学物理 A(1)》.................................................................................................................... 375 《物理实验 A(1)》.................................................................................................................... 375 《复变函数与积分变换》.........................................................................................................375 《离散数学》.............................................................................................................................379 《常微分方程》.........................................................................................................................382 其他专业教学大纲智能科学与技术专业《计算方法》.............................................................................................................................387 信息管理与信息系统专业《离散数学》.............................................................................................................................391 信息安全专业《离散数学》.............................................................................................................................393

V 管理科学专业《离散数学》.............................................................................................................................394 全校公共课《高等数学 A(1)(2)》(普通教学班).........................................................................................395 《高等数学 A(1)(2)》(强化教学班).........................................................................................399 《高等数学 B(1)(2)》(普通教学班).........................................................................................404 《高等数学 B(1)(2)》(强化教学班).........................................................................................408 《高等数学 C(1)(2)》................................................................................................................412 《线性代数 A》......................................................................................................................... 416 《线性代数 B》......................................................................................................................... 418 《概率论与数理统计 A》.........................................................................................................420 《概率论与数理统计 B》......................................................................................................... 423 《复变函数与积分变换 A》.....................................................................................................426 《复变函数与积分变换 B》..................................................................................................... 429 《大学物理 A(1)(2)》................................................................................................................431 《大学物理 B》......................................................................................................................... 437 《物理实验 A(1)(2)》................................................................................................................441 《物理实验 B》......................................................................................................................... 447 《数学实验》.............................................................................................................................452 《数学建模》.............................................................................................................................452 《高等数学(II)》........................................................................................................................458 《矩阵理论及应用》.................................................................................................................460 《普通物理(II)A》.....................................................................................................................463 《人文物理》.............................................................................................................................465 《物理学史》.............................................................................................................................467 《离散数学》.............................................................................................................................469 《统计分析 SPSS 软件应用》..................................................................................................472

信息与计算科学专业《数学分析(1)2)3)》课程编号 0BL09909.10、0BL09903学分总学时 256 实验/上机学时实验：0学时，上机：0学时课程名称数学分析(1)(2)(3) 英文名称 Mathematical Analysis (1)(2)(3) 课程类别必修适用专业信息与计算科学，应用统计学执笔人李国成审核人陈芳先修课程初等数学一、课程的地位与作用本课程是应用统计学专业最重要的基础课之一，是进一步学习后续课程的基础。它的任务是使学生获得极限论、一元函数微积分学、无穷级数与多元函数微积分学等方面的系统知识。通过本课程的讲授有助于培养学生的辩证唯物主义观点，使学生理解数学分析的基本概念，基本掌握数学分析的论证方法，获得较熟练的演算技能和初步应用的能力。二、课程对应的毕业要求通过该课程的学习使学生掌握数学分析的基础知识，得到良好的数学训练，并具有扎实的数学基础和严密的逻辑思维能力，通过该课程学习，针对复杂工程问题，能够理解和评价工程实际对自然环境、社会环境以及可持续发展的影响。培养具有自主学习和终身学习的意识，有不断学习和适应发展的能力。三、课程教学目标熟练掌握数学分析的基本理论和方法，为应用统计学专业打下良好的数学基础。四、课程教学内容提要与基本要求理论部分序号教学内容提要基本要求学时数握确界存在原理.能够利用它们证明简单的相关命题能够利用有理数集的稠密性第章实数集与函数证明相关的简单命题：理解函数的确界的意 .1实数义：熟练掌握函数的四则运算、能够利用绝 12数集确界原理对值不等式讨论函数的有界性和单调性：掌 6 13函数概念操复合函数的概念：掌界利用运算和复合来构 1.4具有某些特性的函数告新函的方法，熟练掌握基本初等函数并熟悉它们的图像，会通过它们构造简单的初气函数第二章数列极限熟练掌程数列极限的定义，能够利用8语 2 2.1数列极限概念言证明数列是否有极限：熟练掌握收敛数列 1

1 信息与计算科学专业《数学分析(1)(2)(3)》课程编号 0BL09909-10、0BL09903 学分 16 总学时 256 实验/上机学时实验：0 学时，上机：0 学时课程名称数学分析（1）（2）（3）英文名称 Mathematical Analysis（1）（2）（3）课程类别必修适用专业信息与计算科学，应用统计学执笔人李国成审核人陈芳先修课程初等数学一、课程的地位与作用本课程是应用统计学专业最重要的基础课之一，是进一步学习后续课程的基础。它的任务是使学生获得极限论、一元函数微积分学、无穷级数与多元函数微积分学等方面的系统知识。通过本课程的讲授有助于培养学生的辩证唯物主义观点，使学生理解数学分析的基本概念，基本掌握数学分析的论证方法，获得较熟练的演算技能和初步应用的能力。二、课程对应的毕业要求通过该课程的学习使学生掌握数学分析的基础知识，得到良好的数学训练，并具有扎实的数学基础和严密的逻辑思维能力，通过该课程学习，针对复杂工程问题，能够理解和评价工程实际对自然环境、社会环境以及可持续发展的影响。培养具有自主学习和终身学习的意识，有不断学习和适应发展的能力。三、课程教学目标熟练掌握数学分析的基本理论和方法，为应用统计学专业打下良好的数学基础。四、课程教学内容提要与基本要求理论部分序号教学内容提要基本要求学时 1 第一章第一章实数集与函数 1.1 1.1 实数 1.2 数集·确界原理 1.3 函数概念 1.4 具有某些特性的函数掌握确界存在原理，能够利用它们证明简单的相关命题；能够利用有理数集的稠密性证明相关的简单命题；理解函数的确界的意义；熟练掌握函数的四则运算、能够利用绝对值不等式讨论函数的有界性和单调性；掌握复合函数的概念；掌握利用运算和复合来构造新函数的方法；熟练掌握基本初等函数并熟悉它们的图像，会通过它们构造简单的初等函数 6 2 第二章第二章数列极限 2.1 数列极限概念熟练掌握数列极限的定义，能够利用-语言证明数列是否有极限；熟练掌握收敛数列 12

理论部分序号物学内容提要基木要求学时 2.2收敛数列的性质的性质，能够通过这些性质对数列的敛散性进 2.3数列极限存在的条件行判断：熟练掌握归结原则，并利用它对数列的敛散性进行判断：熟练掌握单调有界定理，理解Cauchy收敛准则熟练掌握函数极限的定义，并能利用ε-6语第三章函数极限言对简单的初等函数的极限给出证明：熟绮 3.1函数极限概念堂挥函数极限的性质并利用之对相关间题进 32函数极限的性质行讨论：掌握夹逼定理的基本思想：牢记两 3.3函数极限存在的条件个重要极限，并可熟练使用它作相关的计算与 3.4两个重要的极限证明：掌握无穷小和无穷大的定义、性质和关 35 无穷量与无穷大量系：理解阶的概念，能够对于相对简单的无穷小及无穷大的阶进行比较熟练掌挥函数连续性的定义，并能利用-8 语言对简单的函数的连娃性给出证明，掌据第四章函数的连续性连续函数的局部性质并利用之对相关问题进行讨论：掌握闭区间上连续函数的性质并会 4 、连续性 4.2连续函数的性质利用它们证明相关命题：了解判定间断点的 10 43初等函数的连续性方法及间断点的分类：理解反函数的定义、存在性和连续性，并且掌握判断反函数的存在及连性的方法，堂据初等函教的连续性牢记函数导数) 第五章导数和微分 5.1导数的概念法复合函数果 52求导法则导法则：数和由参数方程 53参变量函数的导数定义的函数的求导法则：牢记基本初等函数的 54 高阶导数导勒影。会求简单函数的高阶导数，会利用 .5微分递推的方法确定函数的高阶导数：掌握微分的概今：理解一阶微分形式的不变性熟练掌握可导函数取得极值的必要条掌挥Rolle定理Lagrange中值定理的第六章微分中值定理及其应用明思想，理解Cauchy 定理的内容：熟练掌握 6.1拉格朗日定理和函数的单调 LHospital法则，并会利用LHospital法则求 62柯西中值定理和不定式极限定式的极限；熟练掌握函数的单调性与导函 66.3泰勒公式数的符号之间的关系，会求函数极值：掌握 20 6.4函数的极值与最大（小）值函数的凸凹性与二阶导函数的符号之间的关 6.5函数的凸性与拐点系，会求函数图像的拐点：掌握求函数的渐 6.6函数图像的讨论近线的方法，会利用导函数阶导函数进行函数作图：熟练学握利用中值定理证明不等式的基本方法第七章实数的完备性 71关千实数集完备性的基本定理理解闭区间套定理、有限覆盖定理，理解 7.2闭区间上连续函数性质的证明致密性定理、聚点原理、Cantor定理的证明

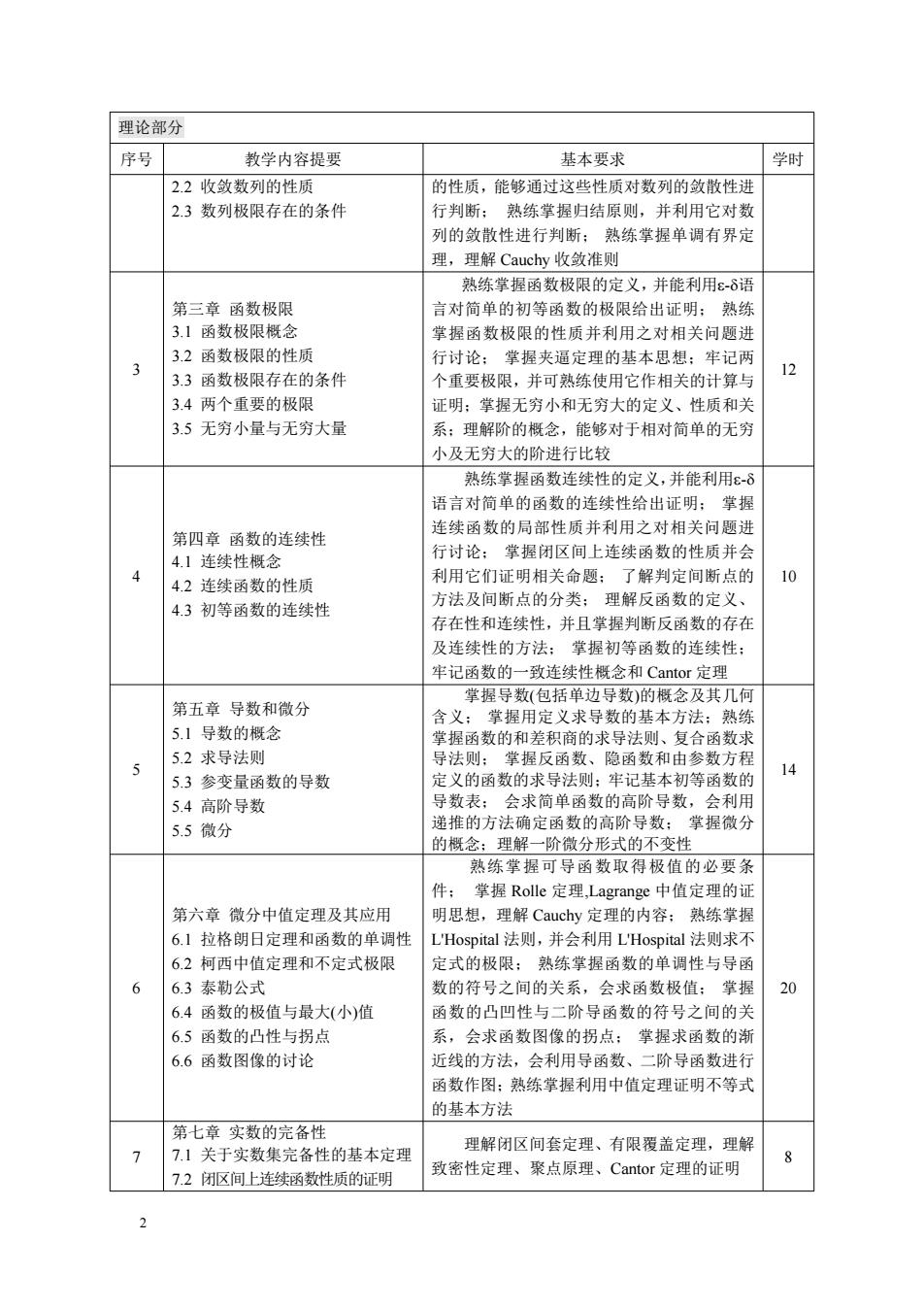
2 理论部分序号教学内容提要基本要求学时 2.2 收敛数列的性质 2.3 数列极限存在的条件的性质，能够通过这些性质对数列的敛散性进行判断；熟练掌握归结原则，并利用它对数列的敛散性进行判断；熟练掌握单调有界定理，理解 Cauchy 收敛准则 3 第三章第三章函数极限 3.1 函数极限概念 3.2 函数极限的性质 3.3 函数极限存在的条件 3.4 两个重要的极限 3.5 无穷小量与无穷大量熟练掌握函数极限的定义，并能利用-语言对简单的初等函数的极限给出证明；熟练掌握函数极限的性质并利用之对相关问题进行讨论；掌握夹逼定理的基本思想；牢记两个重要极限，并可熟练使用它作相关的计算与证明；掌握无穷小和无穷大的定义、性质和关系；理解阶的概念，能够对于相对简单的无穷小及无穷大的阶进行比较 12 4 第四章第四章函数的连续性 4.1 连续性概念 4.2 连续函数的性质 4.3 初等函数的连续性熟练掌握函数连续性的定义，并能利用- 语言对简单的函数的连续性给出证明；掌握连续函数的局部性质并利用之对相关问题进行讨论；掌握闭区间上连续函数的性质并会利用它们证明相关命题；了解判定间断点的方法及间断点的分类；理解反函数的定义、存在性和连续性，并且掌握判断反函数的存在及连续性的方法；掌握初等函数的连续性；牢记函数的一致连续性概念和 Cantor 定理 10 5 第五章第五章导数和微分 5.1 导数的概念 5.2 求导法则 5.3 参变量函数的导数 5.4 高阶导数 5.5 微分掌握导数(包括单边导数)的概念及其几何含义；掌握用定义求导数的基本方法；熟练掌握函数的和差积商的求导法则、复合函数求导法则；掌握反函数、隐函数和由参数方程定义的函数的求导法则；牢记基本初等函数的导数表；会求简单函数的高阶导数，会利用递推的方法确定函数的高阶导数；掌握微分的概念；理解一阶微分形式的不变性 14 6 第六章微分中值定理及其应用 6.1 拉格朗日定理和函数的单调性 6.2 柯西中值定理和不定式极限 6.3 泰勒公式 6.4 函数的极值与最大(小)值 6.5 函数的凸性与拐点 6.6 函数图像的讨论熟练掌握可导函数取得极值的必要条件；掌握 Rolle 定理,Lagrange 中值定理的证明思想，理解 Cauchy 定理的内容；熟练掌握 L'Hospital 法则，并会利用 L'Hospital 法则求不定式的极限；熟练掌握函数的单调性与导函数的符号之间的关系，会求函数极值；掌握函数的凸凹性与二阶导函数的符号之间的关系，会求函数图像的拐点；掌握求函数的渐近线的方法，会利用导函数、二阶导函数进行函数作图；熟练掌握利用中值定理证明不等式的基本方法 20 7 第七章第七章实数的完备性 7.1 关于实数集完备性的基本定理 7.2 闭区间上连续函数性质的证明理解闭区间套定理、有限覆盖定理，理解致密性定理、聚点原理、Cantor 定理的证明 8

理论部分序号教学内容提要基本要求学时第八章不定积分熟练掌握原函数和不定积分的概念以及 8.1不定积分概念与基本积分公式不定积分的基本公式：熟练堂握第一、一换元 82换元积分法与分部积分法法和分部积分法：掌握求有理函数的不定积分 10 8.3有理函数和可化为有理函数自主要步骤：了解求简单的无理函数以及涉及到不定积分的三角函数等超越函数的不定积分的方法第九章定积分熟练掌握定积分的定义及其几何意义：掌握上和与下和及其基本性质：牢记函数可积 9.1定积分概是 9.2牛顿-莱布尼茨公式的充要条件，理解闭区间上连续函数和单调函数的可积性的证明：了解两类可积函数：熟 03日可知条件练掌握定积分的性历，掌握积分第一中值定 94定知分的性微积分学基本定理定积分计理、积分上限函数的定义及其性质：熟练掌 Newton-Leibniz公式、定积分换元法、分部积分法：第十章定积分的应用 10.1平面图形的面积 10.2由平行截面面积求体利掌握平面图形面积、平面上的光滑曲线的狐长、已知被面积的立体体积、旋转体的侧面 10,3平面曲线的弧长与曲到 6 积的计算公式，了解定积分在物理学中的应用 104旋转曲面的面积 10.5定积分在物理中的某些应用第十一章反常积分线性运算法则绝对收敛的概念熟练掌握无 11.1反常积分概念穷限反常积分的比较判别法、狄利克雷 11 112无穷积分的性质与收敛判别 (Dirichlet)判别法、阿贝尔(Abel)判别法 113暇积分的性质与收敛判别了解无界函数反常积分概念，无界函数反常积汁收敛性判别法熟练掌握数项级数收敛的概念与必要家件：堂怪级数敛散性的Cauchy准：孰练堂第十一章数项级数 12.1级数的收敛性操收敛级数的运算性质、正顶级数收敛的各科 12 12.2正项级数判别法，交错级数的Leibniz判别法：了解Abc 14 12.3 一般项级数变换；会使用Abel判别法和Diriche判别法：掌提绝对收敛级数及其基本性质：理解解级数重排问题，了解级数乘积问题理解函数列的概念，能够利用ε-δ语言讨论函数列的一致收敛性：掌捏函数列的一致敛性的Cauchy判别准则：熟练掌握一致收线第十三章函数列与函数项级数的函数列的极限函数的连续性、可积性、可微 3 131一的收敛性性：熟练堂提函顶级数的一致收敛性的M 132一致收敛函数列与函数项级数的性质判别法：掌握函数项级数的致收敛性的 Abel判别法、Dirichlet判别法：致收敛的函数项级数的和函数的连续性、可积性、可微性： 3

3 理论部分序号教学内容提要基本要求学时 8 第八章第八章不定积分 8.1 不定积分概念与基本积分公式 8.2 换元积分法与分部积分法 8.3 有理函数和可化为有理函数的不定积分熟练掌握原函数和不定积分的概念以及不定积分的基本公式；熟练掌握第一、二换元法和分部积分法；掌握求有理函数的不定积分主要步骤；了解求简单的无理函数以及涉及到的三角函数等超越函数的不定积分的方法 10 9 第九章定积分 9.1 定积分概念 9.2 牛顿－莱布尼茨公式 9.3 可积条件 9.4 定积分的性质 9.5 微积分学基本定理·定积分计算熟练掌握定积分的定义及其几何意义；掌握上和与下和及其基本性质；牢记函数可积的充要条件，理解闭区间上连续函数和单调函数的可积性的证明；了解两类可积函数；熟练掌握定积分的性质；掌握积分第一中值定理、积分上限函数的定义及其性质；熟练掌握 Newton-Leibniz 公式、定积分换元法、分部积分法； 18 10 第十章定积分的应用 10.1 平面图形的面积 10.2 由平行截面面积求体积 10.3 平面曲线的弧长与曲率 10.4 旋转曲面的面积 10.5 定积分在物理中的某些应用掌握平面图形面积、平面上的光滑曲线的弧长、已知截面积的立体体积、旋转体的侧面积的计算公式，了解定积分在物理学中的应用 6 11 第十一章反常积分 11.1 反常积分概念 11.2 无穷积分的性质与收敛判别 11.3 瑕积分的性质与收敛判别掌握无穷限反常积分的概念、柯西准则、线性运算法则、绝对收敛的概念，熟练掌握无穷限反常积分的比较判别法、狄利克雷（Dirichlet）判别法、阿贝尔（Abel）判别法。了解无界函数反常积分概念，无界函数反常积分收敛性判别法 10 12 第十二章数项级数 12.1 级数的收敛性 12.2 正项级数 12.3 一般项级数熟练掌握数项级数收敛的概念与必要条件；掌握级数敛散性的 Cauchy 准则；熟练掌握收敛级数的运算性质、正项级数收敛的各种判别法、交错级数的 Leibniz 判别法；了解 Abel 变换；会使用 Abel 判别法和 Dirichlet 判别法；掌握绝对收敛级数及其基本性质；理解解级数重排问题，了解级数乘积问题 14 13 第十三章函数列与函数项级数 13.1 一致收敛性 13.2 一致收敛函数列与函数项级数的性质理解函数列的概念，能够利用-语言讨论函数列的一致收敛性；掌握函数列的一致收敛性的 Cauchy 判别准则；熟练掌握一致收敛的函数列的极限函数的连续性、可积性、可微性；熟练掌握函数项级数的一致收敛性的 M- 判别法；掌握函数项级数的一致收敛性的 Abel 判别法、Dirichlet 判别法；熟练掌握一致收敛的函数项级数的和函数的连续性、可积性、可微性； 14

理论部分序号教学内容提要基木要求学时第十四竞幂级数熟森幂授数的收效城和收效半的 14 141级 10 14.2函数的幂级数展开比较简单的幂级数的和函数利用幂级数显开排行出物篇的的近的计馆第十五章傅里叶级数理望二角级勒和正衣函新系，堂爆十符 Fourier系数的公式：会写出以2π为周期的函 15】使里叶级数 15 数的fourier级数以及奇函数、偶函数的ourie 152以21为周期的函数的展开式 15.3收敛定理的证明级数展开式：掌握Fourier级数的收敛定理、 “面点第十六章多元函数的极限与连续集中的（区域、距离、聚点市性定维空间的 16 16.1平面点集与多元函数 16.2二元函数的极限 8 16.3二元函数的连续性和连续样有界闭区域上的连续函数的诸性质第十七章多元函数微分学深刻理解信导数的概念和全微分的概念及其几何意义：堂根全微公上与信导数之间的 17.1可微性 17 172复合函数微分法关系：熟练掌握多元复合函数的微分法（链式法则)：了解关于多元函数的一阶微分形式的 173方向导数与梯度不变性：理解方向导数的意义：会求多元函 17.4泰勒公式与极值问题数的高阶导数，解多元图数Tyor公式在定理【（程第十八章隐函数定理及其应用隐函数握隐国 181隐函数的 18 18.2隐函数组合求曲线的切线面的切 14 183几何应用元函数的极值的必要条 18.4条件极值件和充分条件的定理、会求二元函数的极值：会用Lagrange乘数法解决条件极值问题令参恋量的知公的性质连续性可和性司第十九章含参量积分微性)，堂握含参套量的广义知分的收敛性和 19.1含参量正常积分 19 一致收敛性：熟练掌握关于含参变量的广义 19.2含参量反常积分积分的一致收敛性的M判别法：掌握一致吸 19.3欧拉积分敛的柯西准则：学含参变量的「义积分的可积性解B 函数的定义并能够熟练地进行相关的运算第二十章曲线积分掌握曲线的方向的概今： 201第一曲线公型曲线积分概念与计算一刑 6 20.2第二型曲线积分曲线积分的概念与计算了解平面图形的面积的定义以及常用的第一十一音币和可的平面图二重积分的概 21.1二重积分概色 22 212直角坐标系下二重积分的计熟练掌式及其算用：熟练掌握曲线积分和积分路径无关的等价

4 理论部分序号教学内容提要基本要求学时 14 第十四章幂级数 14.1 幂级数 14.2 函数的幂级数展开熟练掌握幂级数的收敛域和收敛半径的求法；熟练掌握幂级数的内闭一致收敛性、和函数的性质(连续性、可积性、可微性) ；会求比较简单的幂级数的和函数；能够利用幂级数展开进行比较简单的近似计算 10 15 第十五章傅里叶级数 15.1 傅里叶级数 15.2 以2l 为周期的函数的展开式 15.3 收敛定理的证明理解三角级数和正交函数系；掌握计算 Fourier 系数的公式；会写出以 2为周期的函数的Fourier级数以及奇函数、偶函数的Fourier 级数展开式；掌握 Fourier 级数的收敛定理、理解 Riemann 引理的证明思想 8 16 第十六章多元函数的极限与连续 16.1 平面点集与多元函数 16.2 二元函数的极限 16.3 二元函数的连续性深刻理解平面点集中的(区域、距离、聚点、开集和闭集等)诸概念；帐握二维空间的完备性质(矩形套定理、致密性定理、Cauchy 准则、有限覆盖)；熟练掌握二元函数的极限和连续性、理解累次极限的概念；熟练掌握有界闭区域上的连续函数的诸性质 8 17 第十七章多元函数微分学 17.1 可微性 17.2 复合函数微分法 17.3 方向导数与梯度 17.4 泰勒公式与极值问题深刻理解偏导数的概念和全微分的概念及其几何意义；掌握全微分与偏导数之间的关系；熟练掌握多元复合函数的微分法(链式法则)；了解关于多元函数的一阶微分形式的不变性；理解方向导数的意义；会求多元函数的高阶导数，了解多元函数 Taylor 公式 14 18 第十八章隐函数定理及其应用 18.1 隐函数 18.2 隐函数组 18.3 几何应用 18.4 条件极值掌握隐函数存在定理Ⅰ(关于二元方程所确定的一元隐函数)；熟练掌握隐函数的求导法则；了解隐函数存在定理Ⅱ(一般情况下的隐函数定理)的含义；理解曲线的切向量与曲面的法向量，会求曲线的切线与曲面的切平面；掌握关于取得二元函数的极值的必要条件和充分条件的定理、会求二元函数的极值；会用 Lagrange 乘数法解决条件极值问题 14 19 第十九章含参量积分 19.1 含参量正常积分 19.2 含参量反常积分 19.3 欧拉积分理解含参变量的积分的概念；熟练掌握含参变量的积分的性质(连续性、可积性、可微性)；掌握含参变量的广义积分的收敛性和一致收敛性；熟练掌握关于含参变量的广义积分的一致收敛性的 M-判别法；掌握一致收敛的柯西准则；掌握含参变量的广义积分的性质(连续性、可积性、可微性)；了解-函数、 -函数的定义并能够熟练地进行相关的运算 8 20 第二十章曲线积分 20.1 第一型曲线积分 20.2 第二型曲线积分掌握曲线的方向的概念；熟练掌握第一型曲线积分的概念与计算；熟练掌握第二型曲线积分的概念与计算 6 21 第二十一章重积分 21.1 二重积分概念 21.2 直角坐标系下二重积分的计算了解平面图形的面积的定义以及常用的可求面积的平面图形，理解二重积分的概念；掌握可积的充要条件及可积函数类；熟练掌握二重积分的性质和二重积分的计算(化重积分为累次积分)；熟练掌握 Green 公式及其应用；熟练掌握曲线积分和积分路径无关的等价 22

理论部分序号教学内容提要基本要求学时 21.3格林公式·曲线积分与路线的无关性 21.4二重积分的变量变换掌握三重积分的定义并就 215三重积分 21.6重积分的应用替换（柱坐标变换、球坐标变换）：掌握重积分的简单应用（面积和体积的计算、物体的质量、物体的质心) 了解有关曲面的一些概念（如曲面侧等）：孰练掌握第一型曲面积分的概今和相关计算第二十二章曲面积分会化第一型曲面积分为二重积分：熟练掌折 22.1第一型曲面积分第二型曲面积分的概念：熟练掌握化第二型 22.2第二型曲面积分曲面积分为二重积分的方法：一型出 22.3高斯公式与斯托克斯公式公式及其面积分的关系面积分与第熟练掌握用理解Ga公式和Sokes公式的量表示五、说明本课程需要先修初等数学。在不影响基本要求的前提下，本大纲所列各内容讲授顺序和时数安排，可作适当调整。为避免教学上的难点过于集中，有些内容可先提出并应用，把证明推迟进行，如实数的一些基本定理移到一元函数微分学之后，又如定积分中“上和与下和”， “可积条件”的证明可移到积分法之后。为了有利于中学数学教学的衔接，建议由无限小数开始叙述实数，并由此证明确界原理。本大纲没有专列习题课，授课教师根据教授的教学内容来安排习题课。六、学生成绩考核与评定方式学生成绩评定采取闭卷考试的方式，总评成绩为考试成绩占70%，平时成绩占30% 七、建议教材与参考书建议教材：盛炎平等编著，数学分析（第一版），机械工业出版社，2015.6：参考书：1.陈传璋等编著，数学分析，高等教有出版社，2007.6。 2.刘玉链等编著，数学分析讲义，高等教有出版社，20085。八、课程中英文简介数学分析课程是应用统计学专业最重要的基础课之一，是进一步学习后续课程的基础。它的任务是使学生获得极限论、一元函数微积分学，无穷级数与多元函数微积分学等方面的系统知识。通过本课程的讲授有助于培养学生的辩证唯物主义观点，使学生理解数学分析的基本概念，基本掌握数学分析的论证方法，获得较熟练的演算技能和初步应用的能力。 Mathematical Analysis is one of the most important fundamental courses for the Applied Statistics specialty.It is the basis for the further studies.Its goal is to let students have systematic

5 理论部分序号教学内容提要基本要求学时 21.3 格林公式· 曲线积分与路线的无关性 21.4 二重积分的变量变换 21.5 三重积分 21.6 重积分的应用条件并会利用它们进行计算；熟练掌握二重积分的变量替换(极坐标变换、广义极坐标变换、一般坐标变换)；掌握三重积分的定义并熟练掌握三重积分的计算；掌握三重积分的变量替换(柱坐标变换、球坐标变换)；掌握重积分的简单应用(面积和体积的计算、物体的质量、物体的质心) 22 第二十二章曲面积分 22.1 第一型曲面积分 22.2 第二型曲面积分 22.3 高斯公式与斯托克斯公式了解有关曲面的一些概念（如曲面侧等）；熟练掌握第一型曲面积分的概念和相关计算、会化第一型曲面积分为二重积分；熟练掌握第二型曲面积分的概念；熟练掌握化第二型曲面积分为二重积分的方法；掌握第一型曲面积分与第二型曲面积分的关系；熟练掌握 Gauss 公式及其应用和 Stokes 公式及其应用；理解 Gauss 公式和 Stokes 公式的向量表示 12 五、说明本课程需要先修初等数学。在不影响基本要求的前提下，本大纲所列各内容讲授顺序和时数安排，可作适当调整。为避免教学上的难点过于集中，有些内容可先提出并应用，把证明推迟进行，如实数的一些基本定理移到一元函数微分学之后，又如定积分中“上和与下和”， “可积条件”的证明可移到积分法之后。为了有利于中学数学教学的衔接，建议由无限小数开始叙述实数，并由此证明确界原理。本大纲没有专列习题课，授课教师根据教授的教学内容来安排习题课。六、学生成绩考核与评定方式学生成绩评定采取闭卷考试的方式，总评成绩为考试成绩占 70%，平时成绩占 30%。七、建议教材与参考书建议教材：盛炎平等编著，数学分析（第一版），机械工业出版社，2015.6。参考书：1. 陈传璋等编著，数学分析，高等教育出版社，2007.6。 2. 刘玉链等编著，数学分析讲义，高等教育出版社，2008.5。八、课程中英文简介数学分析课程是应用统计学专业最重要的基础课之一，是进一步学习后续课程的基础。它的任务是使学生获得极限论、一元函数微积分学、无穷级数与多元函数微积分学等方面的系统知识。通过本课程的讲授有助于培养学生的辩证唯物主义观点，使学生理解数学分析的基本概念，基本掌握数学分析的论证方法，获得较熟练的演算技能和初步应用的能力。 Mathematical Analysis is one of the most important fundamental courses for the Applied Statistics specialty. It is the basis for the further studies. Its goal is to let students have systematic