
Bloom Filter for Network Security Haipeng Dai haipengdai@nju.edu.cn 313 CS Building Department of Computer Science and Technology Nanjing University
Bloom Filter for Network Security Haipeng Dai haipengdai@nju.edu.cn 313 CS Building Department of Computer Science and Technology Nanjing University

Bloom Filters Given a set S={xi,x,x3,,xn}on a universe☑, want to answer queries of the form: sy∈S. Bloom filter provides an answer in -“Constant”time(time to hash) -Small amount of space. -But with some probability of being wrong. Alternative to hashing with interesting tradeoffs. 2
2 Bloom Filters Given a set S = {x1, x2, x3, …, xn} on a universe U, want to answer queries of the form: Bloom filter provides an answer in ─ “Constant” time (time to hash). ─ Small amount of space. ─ But with some probability of being wrong. Alternative to hashing with interesting tradeoffs. Is y ∈ S

Bloom Filters Start with an m bit array,filled with 0s. B 000 0 0 0 0 0 10 0 0 0 0 Hash each item x;in Sk times.If H(x)=a,set B[a]=1. 0100101001110110 B To check if y is in S,check B at H(y).All k values must be 1. B 0100101001110110 Possible to have a false positive;all k values are 1,but y is not in S. B0100101001110110 n items m cn bits k hash functions 3
3 Bloom Filters Start with an m bit array, filled with 0s. Hash each item xj in S k times. If Hi (xj ) = a, set B[a] = 1. B 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 B 0 1 0 0 1 0 1 0 0 1 1 1 0 1 1 0 To check if y is in S, check B at Hi (y). All k values must be 1. B 0 1 0 0 1 0 1 0 0 1 1 1 0 1 1 0 B 0 1 0 0 1 0 1 0 0 1 1 1 0 1 1 0 Possible to have a false positive; all k values are 1, but y is not in S. n items m = cn bits k hash functions

False positive Probability Pr(specific bit of filter is 0)is p'=(1-l/m)m≈em/m=p If p is fraction of 0 bits in the filter then false positive probability is (1-p)≈(1-p')≈(1-p)*=(1-ek1c) Approximations valid as p is concentrated around E[p]. -Martingale argument suffices. Find optimal at k =(In 2)m/n by calculus. -So optimal fpp is about (0.6185)/m n items m cn bits k hash functions 4
4 False Positive Probability Pr(specific bit of filter is 0) is If ρ is fraction of 0 bits in the filter then false positive probability is Approximations valid as ρ is concentrated around E[ρ]. ─ Martingale argument suffices. Find optimal at k = (ln 2)m/n by calculus. ─ So optimal fpp is about (0.6185)m/n k k k k c k (1 ) (1 p') (1 p) (1 e ) − / − ρ ≈ − ≈ − = − n items m = cn bits k hash functions p m p kn kn m ≡ − ≈ ≡ − / ' (1 1/ ) e
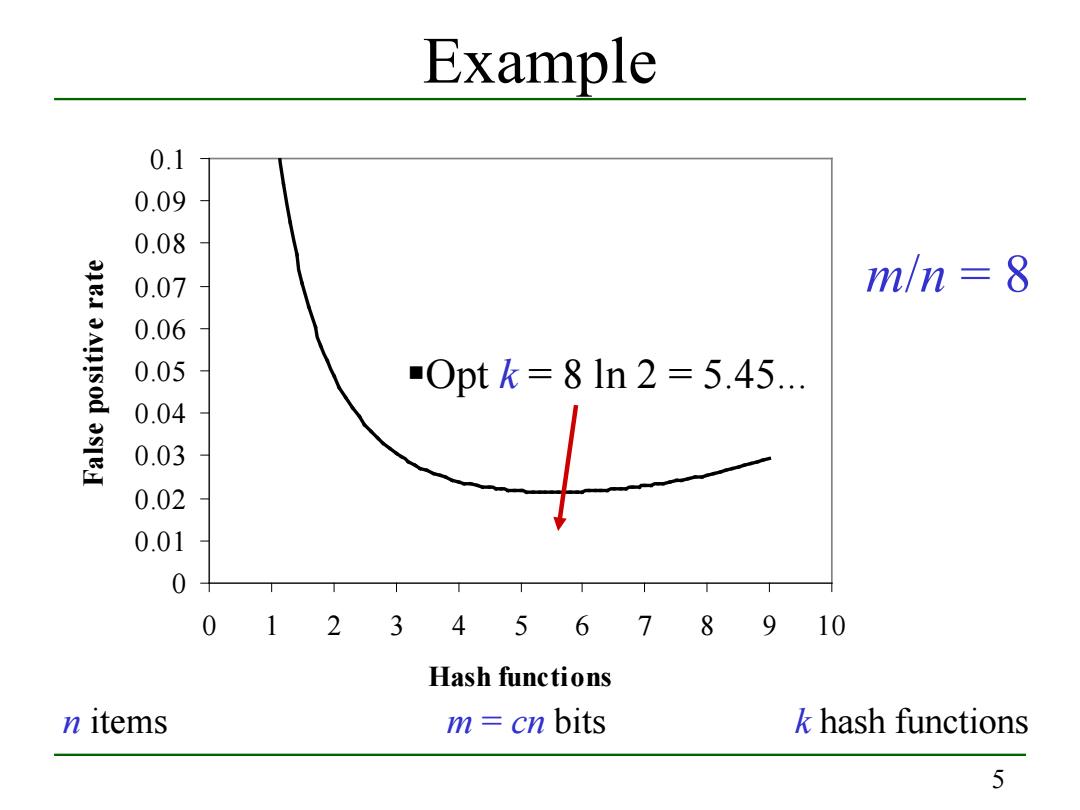
Example 0.1 0.09 0.08 0EI 0.07 m/n=8 0.06 0.05 0ptk=8ln2=5.45.… 0.04 0.03 0.02 0.01 0 0 12345678 910 Hash functions n items m cn bits k hash functions 5
5 Example 0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1 0 1 2 3 4 5 6 7 8 9 10 Hash functions False positive rate m/n = 8 Opt k = 8 ln 2 = 5.45... n items m = cn bits k hash functions
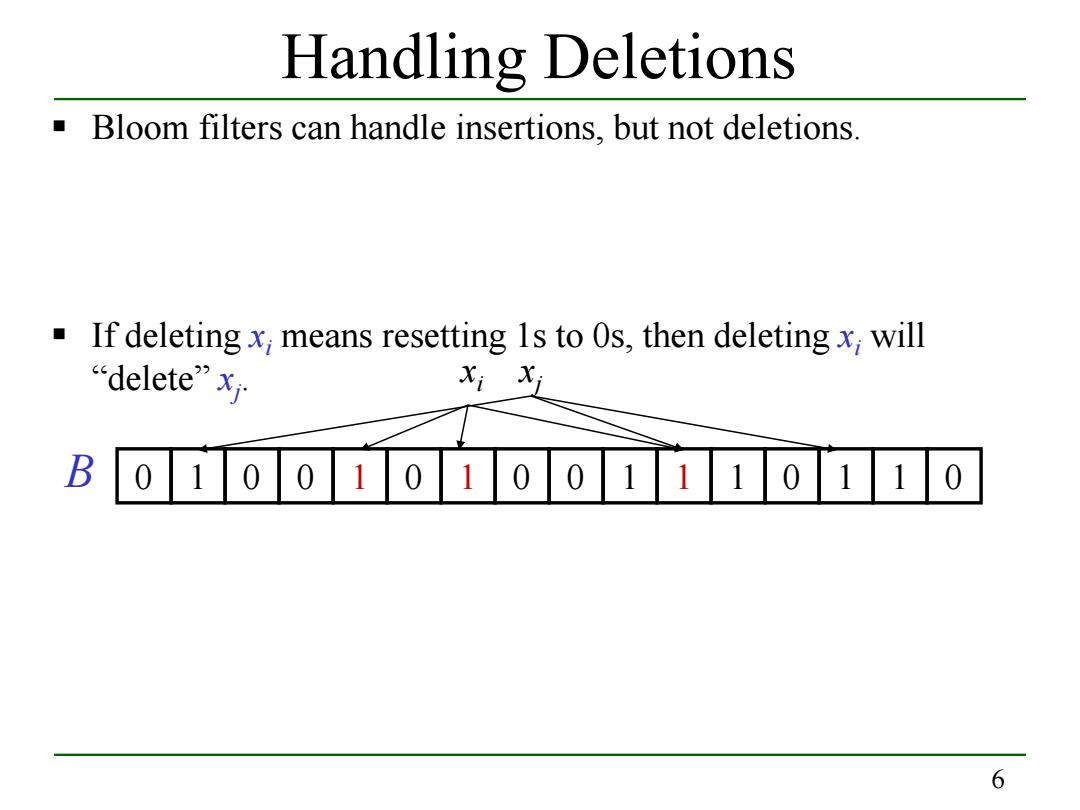
Handling Deletions Bloom filters can handle insertions,but not deletions. If deleting x;means resetting 1s to 0s,then deleting x;will delete”xy Xi Xi B 0100101001110110 6
6 Handling Deletions Bloom filters can handle insertions, but not deletions. If deleting xi means resetting 1s to 0s, then deleting xi will “delete” xj . B 0 1 0 0 1 0 1 0 0 1 1 1 0 1 1 0 xi xj

Counting Bloom Filters Start with an m bit array,filled with 0s. B 000000000000 0 000 Hash each item x;in Sk times.If H(x)=a,add 1 to B[a]. B 0300102003210210 To delete x,decrement the corresponding counters. B 0200002003210110 Can obtain a corresponding Bloom filter by reducing to 0/1 B 0100001001110110 7
7 Counting Bloom Filters Start with an m bit array, filled with 0s. Hash each item xj in S k times. If Hi (xj ) = a, add 1 to B[a]. B 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 B 0 3 0 0 1 0 2 0 0 3 2 1 0 2 1 0 To delete xj decrement the corresponding counters. B 0 2 0 0 0 0 2 0 0 3 2 1 0 1 1 0 Can obtain a corresponding Bloom filter by reducing to 0/1. B 0 1 0 0 0 0 1 0 0 1 1 1 0 1 1 0

Counting Bloom Filters:Overflow Must choose counters large enough to avoid overflow. Poisson approximation suggests 4 bits/counter. -Average load using k=(In 2)m/n counters is In 2. -Probability a counter has load at least 16: Failsafes possible. We assume 4 bits/counter for comparisons. ≈en2(In2)16/16l≈6.78E-17 8
8 Counting Bloom Filters: Overflow Must choose counters large enough to avoid overflow. Poisson approximation suggests 4 bits/counter. ─ Average load using k = (ln 2)m/n counters is ln 2. ─ Probability a counter has load at least 16: Failsafes possible. We assume 4 bits/counter for comparisons. (ln 2) /16! 6.78E 17 ln 2 16 ≈ ≈ − − e
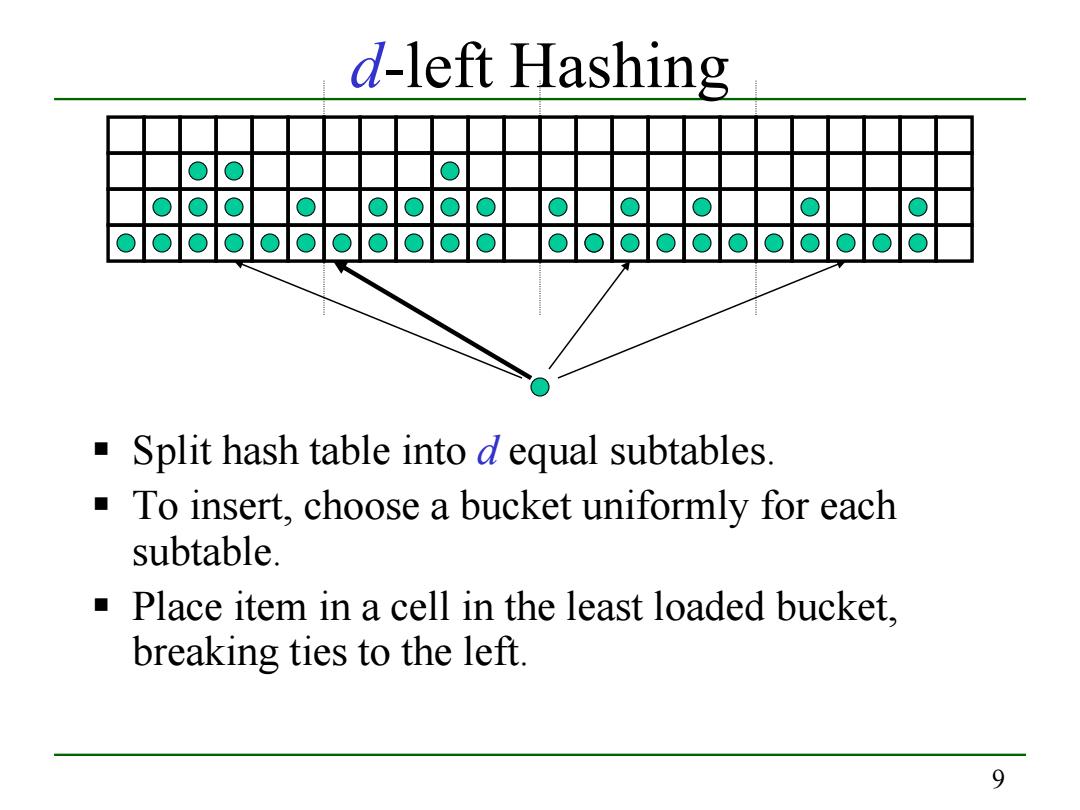
d-left Hashing ooooooooooo■ oooooooooo■ Split hash table into d equal subtables To insert,choose a bucket uniformly for each subtable. Place item in a cell in the least loaded bucket. breaking ties to the left. 9
9 d-left Hashing Split hash table into d equal subtables. To insert, choose a bucket uniformly for each subtable. Place item in a cell in the least loaded bucket, breaking ties to the left

Properties of d-left Hashing Analyzable using both combinatorial methods and differential equations. -Maximum load very small:O(log log n). -Differential equations give very,very accurate performance estimates. Maximum load is extremely close to average load for small values of d. Power of 2 choices! 10
10 Properties of d-left Hashing Analyzable using both combinatorial methods and differential equations. ─ Maximum load very small: O(log log n). ─ Differential equations give very, very accurate performance estimates. Maximum load is extremely close to average load for small values of d. Power of 2 choices!