
Bloom Filters and its variants Original Author:Deke Guo Revised by Haipeng Dai Nanjing University 2015.11.27 Page 1
Page 1 Bloom Filters and its Variants Original Author: Deke Guo Revised by Haipeng Dai Nanjing University 201 5.11.27

Outline 1.Standard Bloom Filters 2.Compressed Bloom Filters 3.Counting Bloom Filters 4.Representation of a set of(key,f(key)) 5.Invertible Bloom Filters Page 2
Outline 1. Standard Bloom Filters 2. Compressed Bloom Filters 3. Counting Bloom Filters 4. Representation of a set of (key, f(key)) 5. Invertible Bloom Filters Page 2

The main point ▣ Whenever you have a set or list,and space is an issue,a Bloom filter may be a useful alternative. 3
3 The main point Whenever you have a set or list, and space is an issue, a Bloom filter may be a useful alternative

The Problem Solved by BF: Approximate Set Membership ☐ Given a set S={x.),construct data structure to answer queries of the form"Is y in S?" Data structure should be: Fast(Faster than searching through S). ■ Small(Smaller than explicit representation) To obtain speed and size improvements,allow some probability of error. ■ False positives:y gs but we reportyeS ■False negatives:y∈S but we reporty &S
4 The Problem Solved by BF: Approximate Set Membership Given a set S = { x 1,x 2,…,x n }, construct data structure to answer queries of the form “Is y in S?” Data structure should be: Fast (Faster than searching through S). Small (Smaller than explicit representation). To obtain speed and size improvements, allow some probability of error. False positives: y S but we report y S False negatives: y S but we report y S
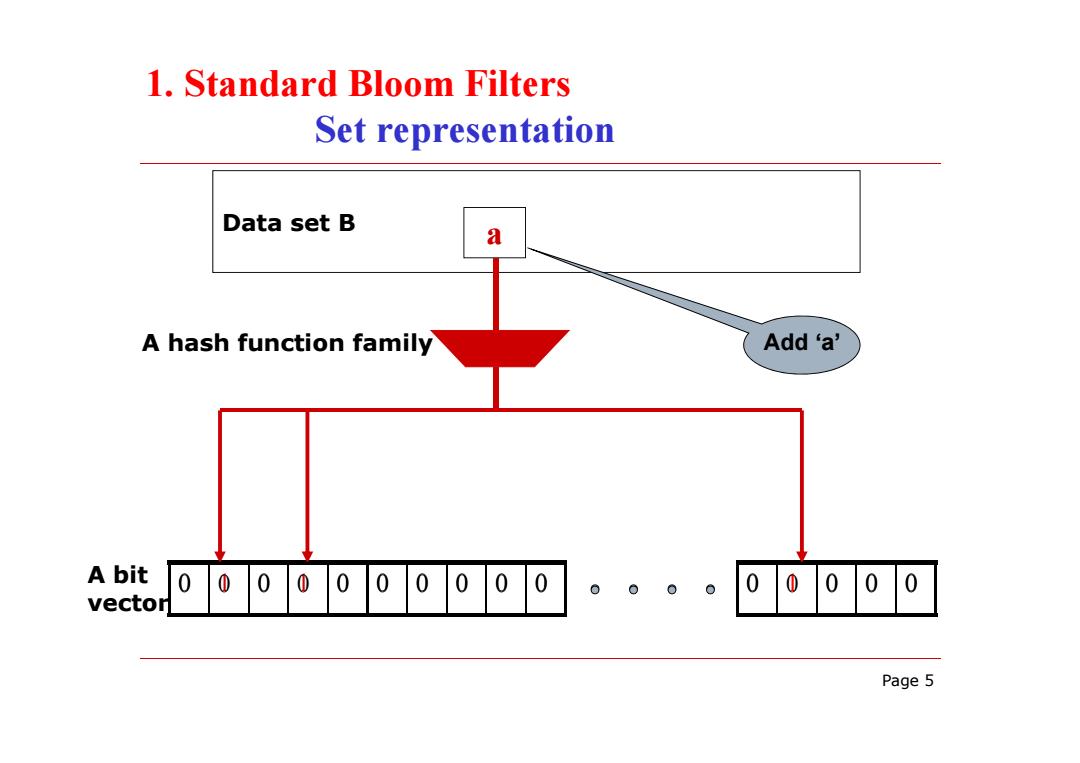
1.Standard Bloom Filters Set representation Data set B a A hash function family Add 'a' A bit 0000000000 0 00 00000 vector Page 5
Page 5 Data set B 0 1 0 1 0 0 0 0 0 0 0 1 0 0 0 a A hash function family A bit vector 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1. Standard Bloom Filters Set representation Add ‘a’
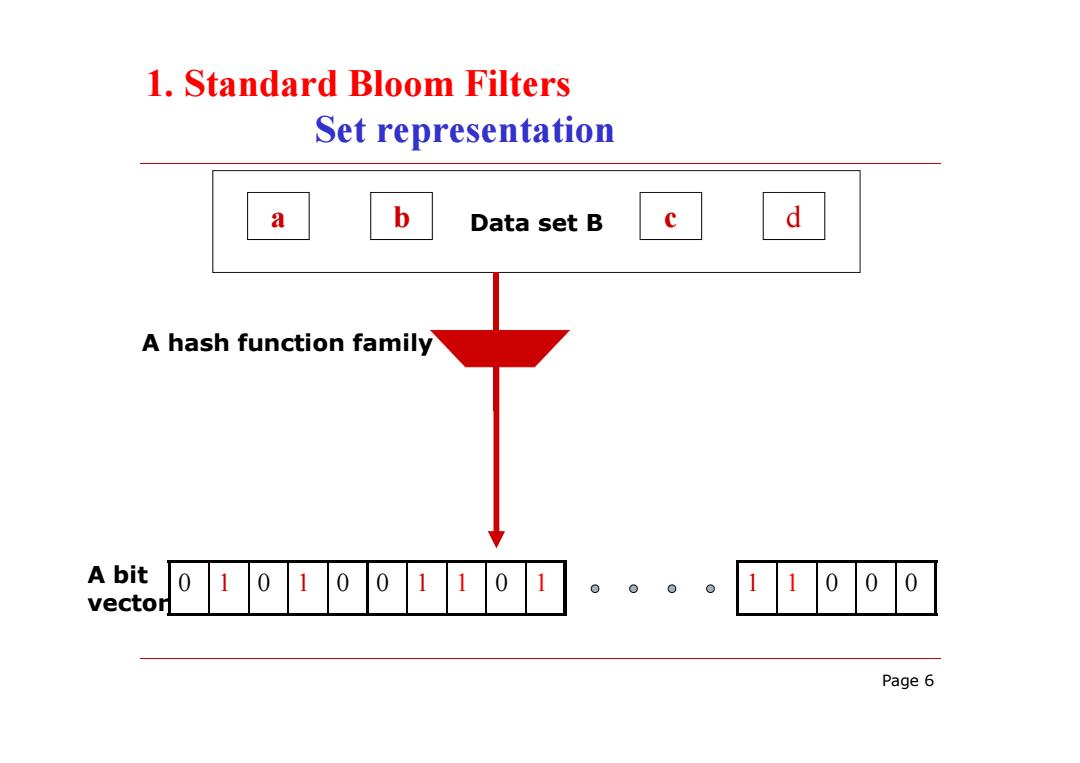
1.Standard Bloom Filters Set representation a b Data set B d A hash function family A bit vector Page 6
Page 6 0 1 0 1 0 0 1 1 0 1 1 1 0 0 0 a b Data set B c d A hash function family A bit vector 1. Standard Bloom Filters Set representation

1.Standard Bloom Filters Membership query ▣“Constant''time(time to hash) Small amount of space. But with some probability of being wrong. 7
7 “Constant” time (time to hash). Small amount of space. But with some probability of being wrong. 1. Standard Bloom Filters Membership query
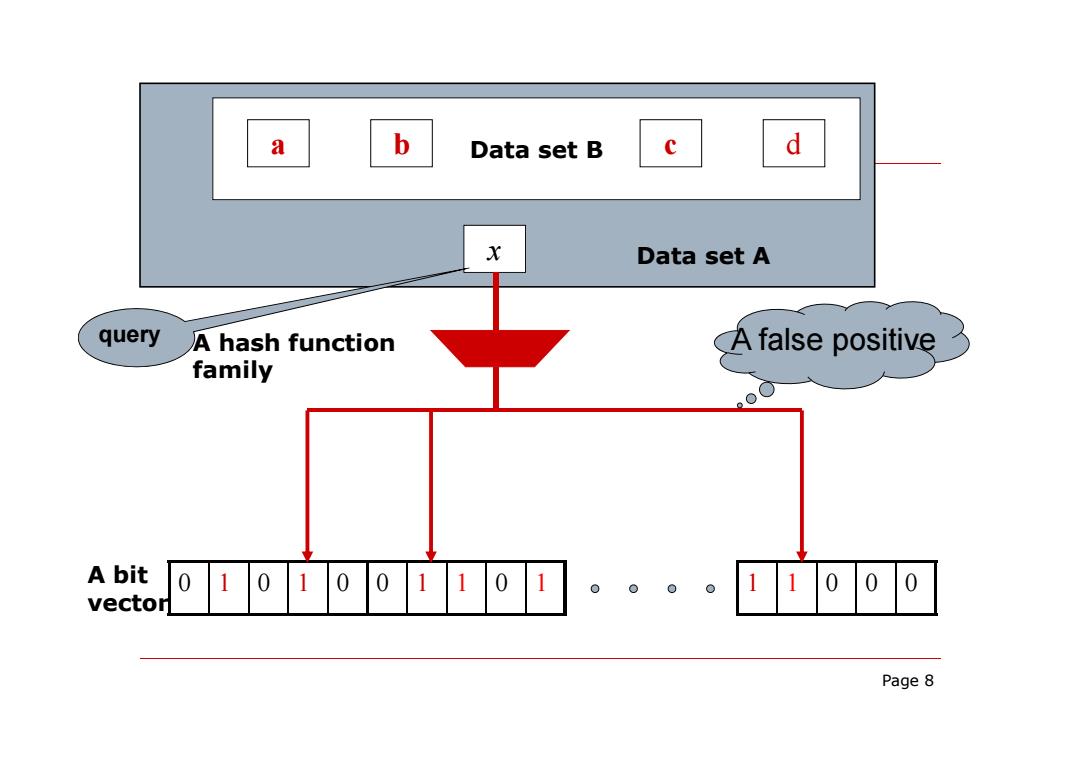
a b Data set B d Data set A query A hash function A false positive family A bit 01o1001101 vector 。。。。000 Page 8
Page 8 0 1 0 1 0 0 1 1 0 1 1 1 0 0 0 a b Data set B c d x Data set A A hash function family A bit vector query A false positive

False positive probability Assumption:We have good hash functions,look random. Given m bits for filter and n elements,choose number k of hash functions to minimize false positives: ■Let p=Pr[cell is empty ]=(1-1/m)kne-kn/m ■Let f=Pr[false pos]=(1-p)(1-e-kn/m As k increases,more chances to find a 0,but more 1's in the array. Find optimal at k=(In 2)m/n by calculus. f=Pr[false pos]=0.61285mlm 9
9 False positive probability Assumption: We have good hash functions, look random. Given m bits for filter and n elements, choose number k of hash functions to minimize false positives: Let Let As k increases, more chances to find a 0, but more 1’s in the array. Find optimal at k = (ln 2) m / n by calculus. kn kn m p m e / Pr[cell is empty ] ( 1 1 / ) k kn m k f Pr[false pos ] ( 1 p ) ( 1 e ) / / Pr[false pos] 0.61285m n f
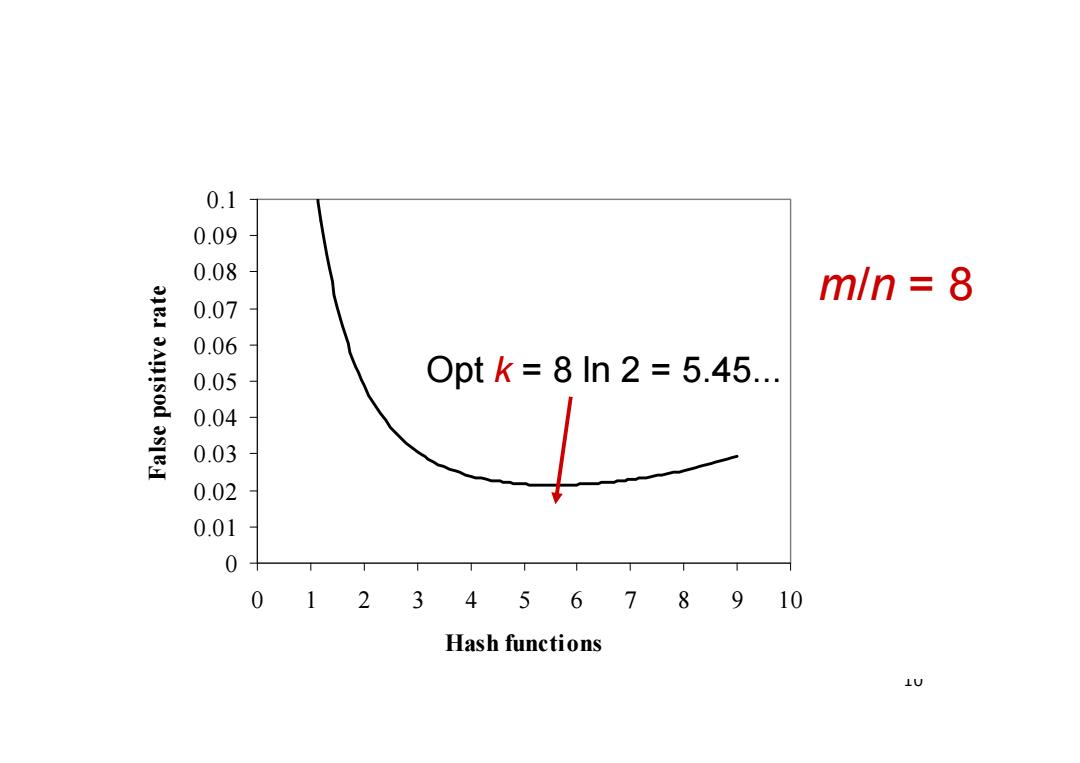
0.1 0.09 0.08 0JEI m/n=8 0.07 0.06 0.05 0ptk=8ln2=5.45.. 0.04 OSIEH 0.03 0.02 0.01 0 012345678910 Hash functions 10
10 0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1 0 1 2 3 4 5 6 7 8 9 10 Hash functions False positive ratem/n = 8 Opt k = 8 ln 2 = 5.45