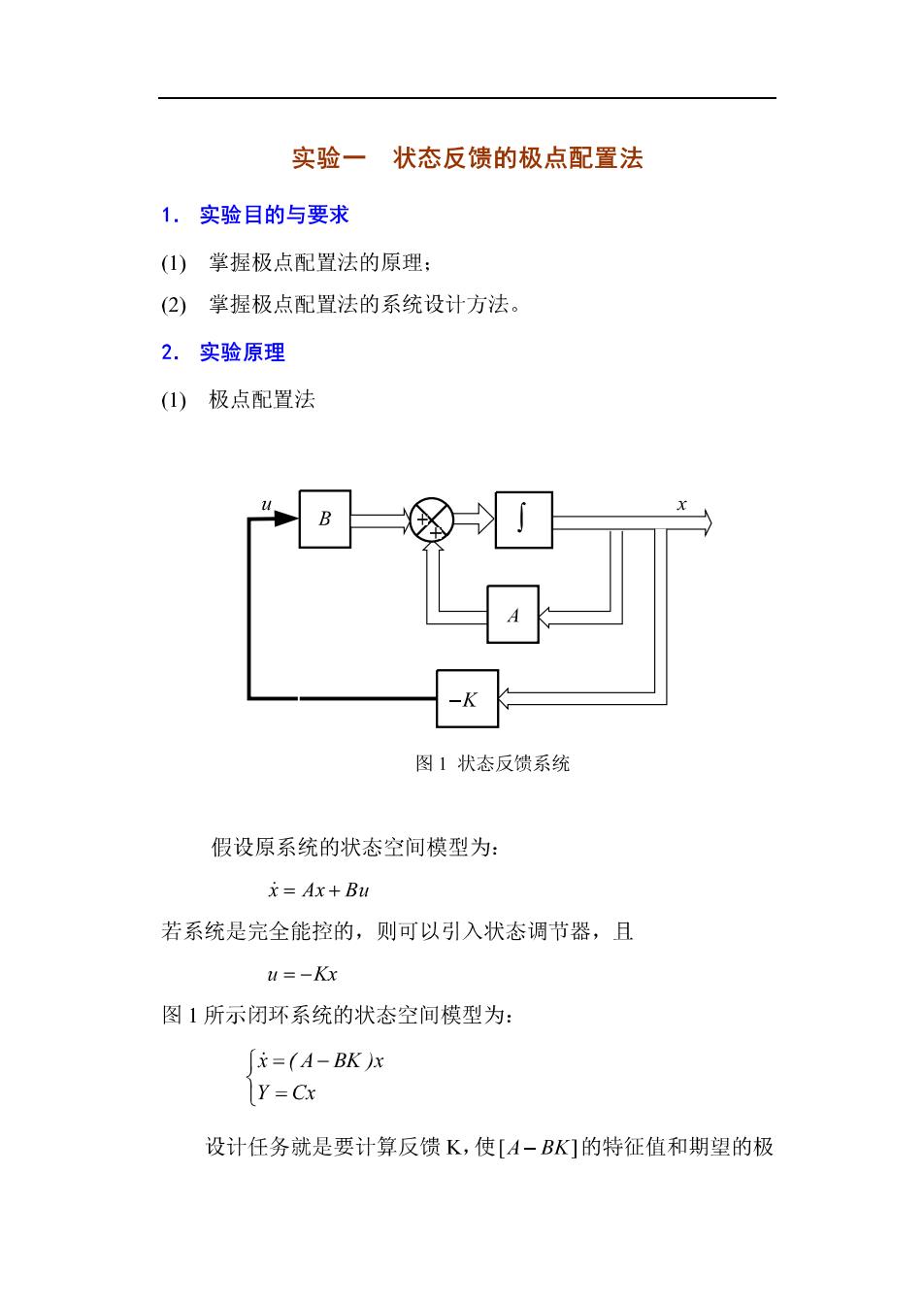
实验一状态反馈的极点配置法 1.实验目的与要求 (①)掌握极点配置法的原理: (2)掌握极点配置法的系统设计方法。 2.实验原理 (1)极点配置法 图1状态反馈系统 假设原系统的状态空间模型为 元=Ax+Bu 若系统是完全能控的,则可以引入状态调节器,且 u=-Kx 图1所示闭环系统的状态空间模型为: =(A-BK)x ]Y=Cx 设计任务就是要计算反馈K,使[A-BK]的特征值和期望的极

点P相同。 (2)极点配置的MATLAB函数 对于单输入单输出系统,求解反馈增益的函数调用格式为: K acker(A,B,P) 其中,A,B为系统矩阵:P为期望向量:K为反馈增益向量。 对于单(或多)输入-单(或多)输出系统,求解反馈增益 的函数调用格式为: K=place(A,B,P) [K,prec,message]=place(A,B,P) 其中,prec为实际极点偏离期望极点位置的误差:message是当系 统某一非零的极点偏离期望位置大于10%时给出警告信息。 3.实验内容与步骤 (1)仿真实验 利用MATLAB进行基于极点配置的系统设计内容和步骤如下: ①对于给定被控对象,获得状态反馈闭环系统的状态空间模型: ②根据系统动态性能要求,确定期望极点分布P: a.利用MATLAB极点配置设计函数place或acker,求取系统反馈 增益K: b.检验系统性能。 1 以系统传递函数为G(s)= 6+6s+12为例,给出用MATLAB 编写求反馈增益K的程序(要求通过状态反馈使系统闭环极点配 置在-100,-7.07±7.071位置上):

%The original system: %=========== ys=zpk([],[0,-6,-12],1); %The desired poles: %========== P=[-100,-7.07+7.07i,-7.07-7.07i]; %Convert system model to state space %三============= sys=ss(sys); [A,B,C,D]=ssdata(sys); disp('Feedback gain : K=acker(A,B,P) New open loop system: %===二========三 sysopen=ss(A,B,K,0); %New closed-loop system: %==========兰=== sysclose=ss(A-B*K,B,C,D); disp('Poles of new closed-loop system:); poles=pole(sysclose) step(sysclose/dcgain(sysclose),2); (2)硬件实验 设计出系统的模拟电路图,并利用控制理论实验箱搭建该系 统模拟电路,以进行实验验证。要求记录示波器的结果,并与软 件仿真结果进行比较。 4.思考与分析 (1)进行极点配置设计时,对原系统的要求是什么? (2)对于一个给定的系统,反馈增益K是唯一的吗?为什么?