
第二章机电传动系统的动力学基础 √机电传动系统的运动方程式 √多轴传动系统中负载转矩、转动惯量和飞轮转矩的折算 √典型生产机械的负载特性 √机电传动系统稳定运行的条件 √机电传动系统的过渡过程

章节内容 2.1单轴拖动系统的运动方程式 2.2多轴拖动系统的简化 2.3生产机械的机械特性 2.4机电系统稳定运行的条件 2.4机电传动系统的过渡过程(自学)

2.1单轴拖动系统的运动方程式 一、单轴拖动系统的组成 电动机 电动机的驱动对象 九 +n 连接件 系统结构图 转距方向 电动机M通过连接件直接与生产机械相连,由电动机M产生输 出转矩TM,用来克服负载转矩TL,带动生产机械以角速度ω(或 速度n)进行运动

运动方程式 在机电系统中,同一根轴上 根据动力学原理: Tm、TL、o(或n)之间的函数关系 TM -TL=Jdo 称为运动方程式。 =J2πdn 运动方程式 60 dt Ty -Tt Ta 转矩平衡方程式 TM一电动机的输出转矩(Nm) n一速度(rmin) -负载转矩(N.m) o-角速度(rad/s) J-转动惯量(kg.m2) t一时间(s) a=o=2红d dt 60d-动态转矩(N.m)

,传动系统的状态 根据运动方程式可知:运动系统有两种不同的运动状态: 1稳态(TM=T时): 2.动态(TM≠时): =0=0 >时:a=Jde >0 =0 即d。>0,加速运动。 即 d1 dt 1<时:7-J0, 传动系统以恒速运动。 TM=T时传动系统 即<0,诚速运动。 处于恒速运动的这种状 TM≠TL时传动系统处于加 速或减速运动的这种状态被称 态被称为稳态。 为动态

四,T,T、n的参考方向 因为电动机和生产机械以共同的转速旋转,所以,一般以® (或n)的转动方向为参考来确定转矩的正负。 拖动转距促进运动;制动转距阻碍运动。 1.T的符号与性质 cn) 当T的实际作用方向与n的 方向相同时,取与n相同的符号; 当T的实际作用方向与n的 +T1 方向相反时,取与n相反的符号; TM -TL=Jdo 当T的实际作用方向与n的 方向相同(符号相同)时,T =J2πdn 60 dt 为拖动转距,否则为制动转距

四,T,T、n的参考方向 因为电动机和生产机械以共同的转速旋转,所以,一般以ω (或)的转动方向为参考来确定转矩的正负。 拖动转距促进运动;制动转距阻碍运动。 2.T的符号与性质 当T的实际作用方向与n的方向 相同时,取与n相反的符号; 当T的实际作用方向与n的方向 相反时,取与n相同的符号; TM-Ti =Jdo 当T的实际作用方向与n的方 向相同(符号相反)时,T为拖 =J2 dn 60 dz 动转距,否则为制动转距
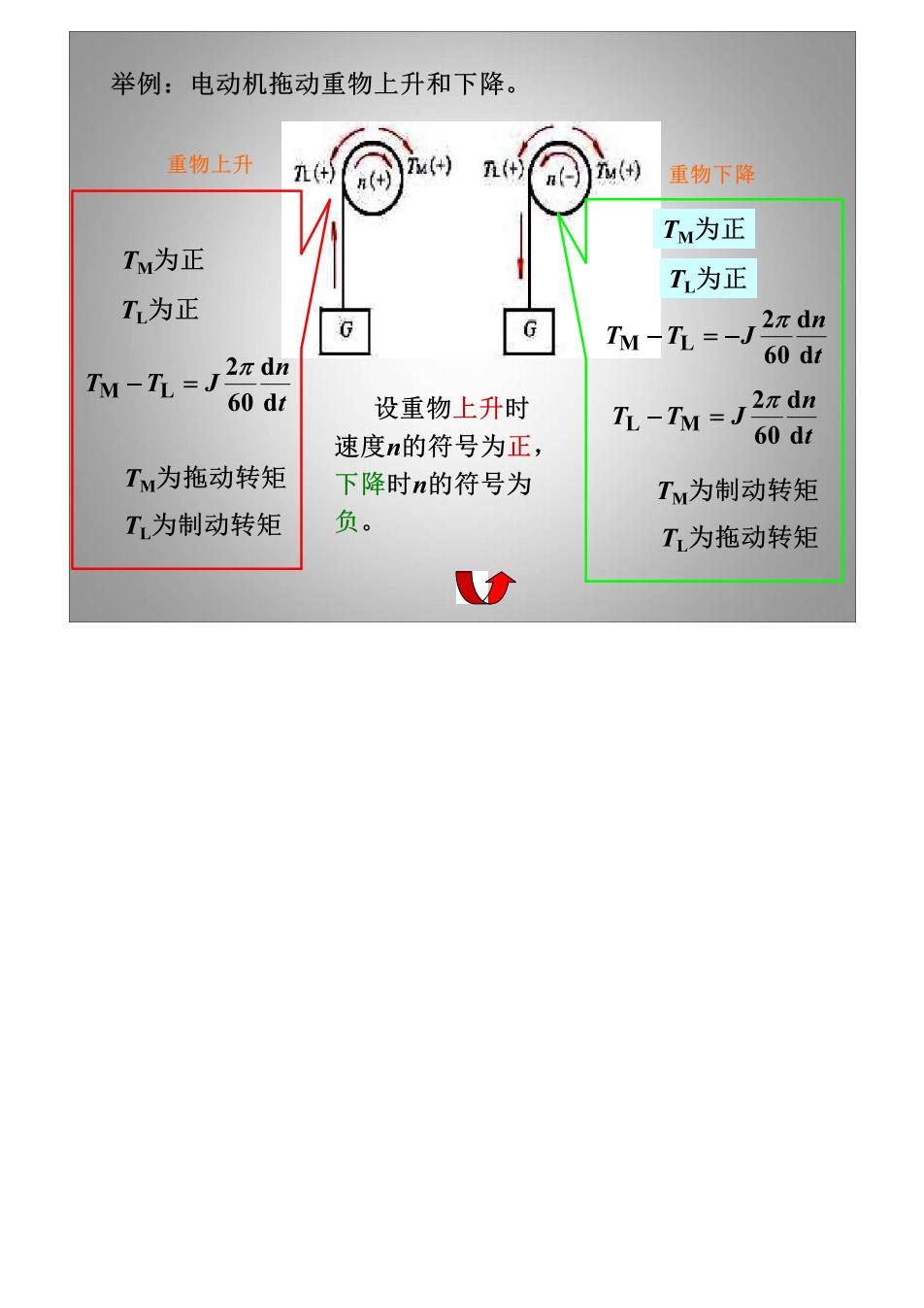
举例:电动机拖动重物上升和下降。 重物上升 重物下降 TM为正 TM为正 T为正 T为正 TM-T =-J2z dn TM-T=J2z dn 60 dz 60 dz 设重物上升时 TL-In =J2z dn 速度n的符号为正, 60 dz TM为拖动转矩 下降时n的符号为 TM为制动转矩 T为制动转矩 负。 T为拖动转矩

2.2多轴拖动系统的简化 一、多轴拖动系统的组成 电动机通过减速机与生产机械相连。 D G 旋转运动 直线运动 为了对多轴拖动系统进行运行状态的分析,一般是将多轴拖动 系统等效折算为单轴系统,再用单轴系统的分析方法分析多轴系统

三、负载转矩的折算 由于转矩是静态转矩,因此折算的原则是:静态时,折算前 后系统总的传输功率不变。 设电动机以®,角速度旋转,折算到电动机轴上的负载转矩 为Ta:对应生产机械的旋转速度为@L,负载转矩为T。 则电动机输出功率 PM=oM·Tg 负载所需功率 h=0L·T