
《机电传动控制》 部分课后习题及答案

2.1从运动方程式怎样看出系统是加速的、减速的、稳定的和静 止的各种工作状态? 答:运动方程式: Ty-TL=J dw dt Ty -TL=Ta T>0时:系统加速;T0时:系统稳速; T<0时,系统减速或反向加速

2.2说明机电传动系统运动方程式中的拖动转矩、静态转矩和动 态转矩的概念。 答:拖动转矩:电动机产生的转矩Tm或负载转矩T,与转速相同时,就是 拖动转矩。 静态转矩:电动机轴上的负载转矩T,它不随系统加速或减速而变化。 动态转矩:系统加速或减速时,存在一个动态转矩T,它使系统的运 动状态发生变化
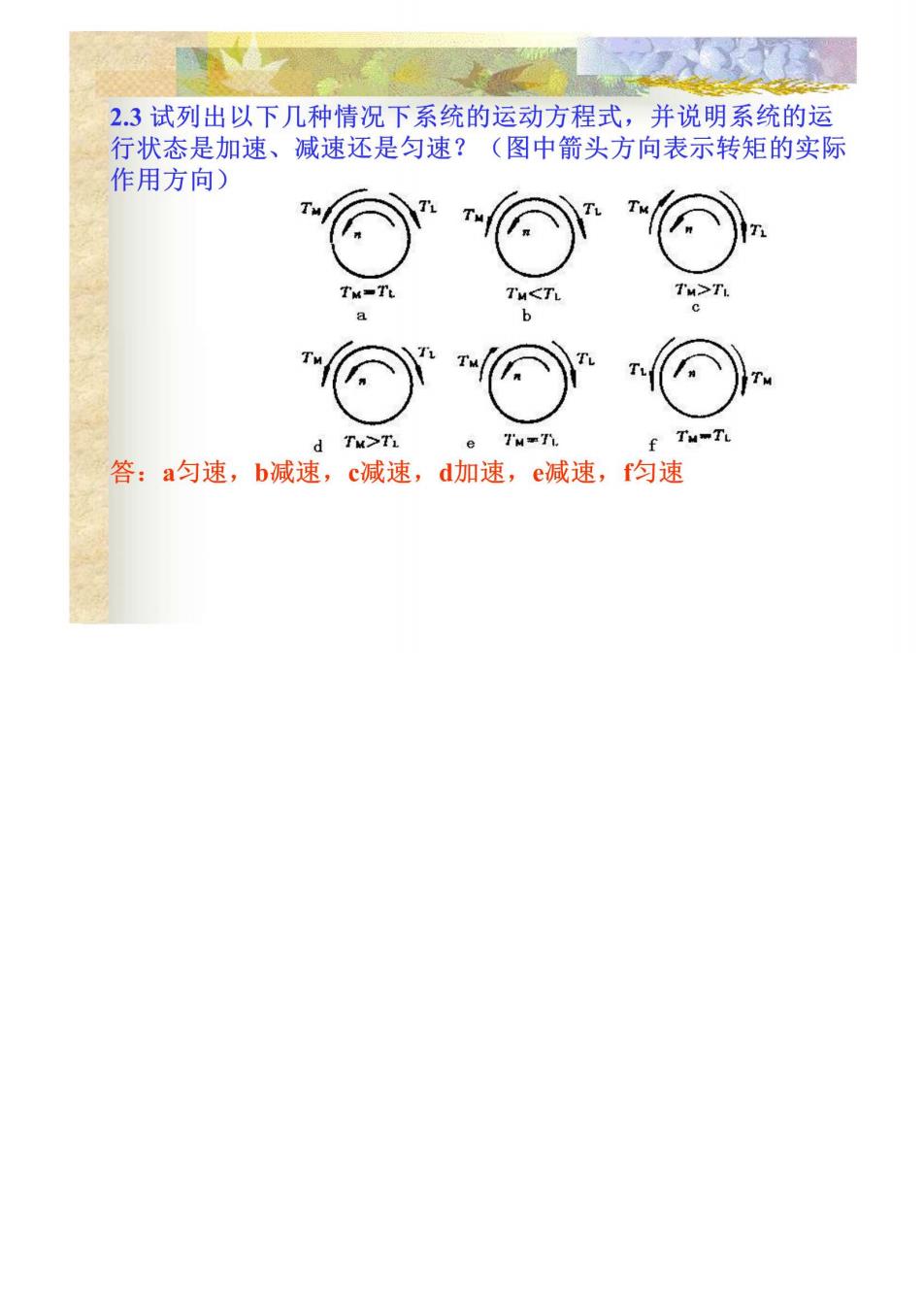
2.3试列出以下几种情况下系统的运动方程式,并说明系统的运 行状态是加速、减速还是匀速?(图中箭头方向表示转矩的实际 作用方向) T TuT TH-TY T TH>TL 答:a匀速,b减速,c减速,d加速,e减速,f匀速

2.4多轴拖动系统为什么要折算成单轴拖动系统?转矩折算为什 么依据折算前后功率不变的原则?转动惯量折算为什么依据折算 前后动能不变的原则? 答:在多轴拖动系统情况下,为了列出这个系统运动方程,必须先把各传动 部分的转矩和转动惯量或直线运动部分的质量都折算到电动机轴上。 由于负载转矩是静态转矩,所以可根据静态时功率守恒原则进行折算。 由于转动惯量和飞轮转矩与运动系统动能有关,所以可根据动能守恒原 则进行折算

2.5为什么低速轴转矩大?调速轴转矩小? 答:忽略磨擦损失的情况下,传动系统的低速轴和调速轴传递的 功率是一样的,即P,=P2 而P1=T101P2=T202 所以T101=T202”当01>0时,T,<T2

2.6为什么机电传动系统中低速轴的GD2比高速轴的GD2大得 套?因为低速轴的转矩大,所设计的低速轴的直径及轴上的齿轮 等零件尺寸大,质量也大,所以GD大,而高速轴正好相反

2.7如图所示,电动机轴上的转动惯量J=2.5kg.m2,转速nM= 900r/mim;中间传动轴的转动惯量J1=2kg.m2,转速n1= 300rmim;生产机械轴的惯量J=16kg.m2,转速nu=60r/mim 试求折算到电动机轴上的等效转动惯量。 ☒ 答:j=0/o=n/m,-900/300=3 jL=0w/oL=nwmL-=900/60=15 216 Jz=Jy+ +=2.5+ 2+152 =2.8(kg·m)
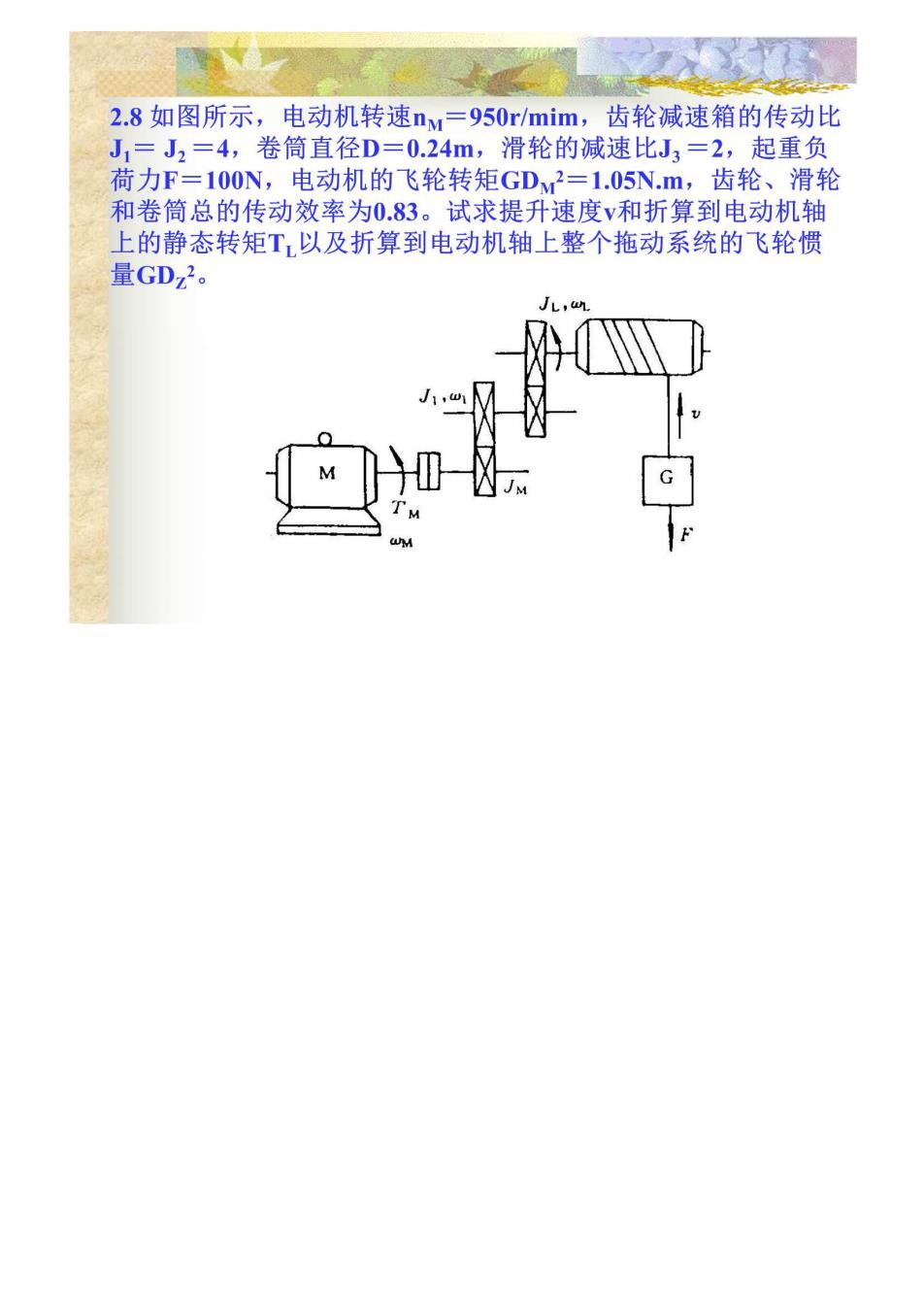
2.8如图所示,电动机转速n,=950rmim,齿轮减速箱的传动比 J1=J2=4,卷筒直径D=0.24m,滑轮的减速比J3=2,起重负 荷力F=100N,电动机的飞轮转矩GD、2=1.05N.m,齿轮、滑轮 和卷筒总的传动效率为0.83。试求提升速度v和折算到电动机轴 上的静态转矩T以及折算到电动机轴上整个拖动系统的飞轮惯 量GDz2

答: n,= nM 950 4×4 =59.4(r/min) πDn, V= 元×0.24×594=0.37(m1s) 60j3 60×2 T1=9.55Fv/(n1n)-9.55×100×0.37/(0.83×950)=0.45N.m GD=6GD2+365m2 n GD=0.11.25)x1.05+365×100x0372-1.16132N-m2 9502