
第7章采样 sampling
第7章 采样 sampling

本章主要讨论的问题有 1. 首先介绍并建立采样的概念和从样本值重建一个 连续时间信号的过程。 2. 一个连续时间信号能真正由它的样本值恢复出来 的条件,并研究当这些条件不满足时所产生的后 果。 3. 研究经由采样已经变换到离散时间信号的连续时 间信号处理。 4. 讨论离散时间的采样,以及有关的抽取和内插的 概念
本章主要讨论的问题有 1. 首先介绍并建立采样的概念和从样本值重建一个 连续时间信号的过程。 2. 一个连续时间信号能真正由它的样本值恢复出来 的条件,并研究当这些条件不满足时所产生的后 果。 3. 研究经由采样已经变换到离散时间信号的连续时 间信号处理。 4. 讨论离散时间的采样,以及有关的抽取和内插的 概念

7.0引言 在一定条件下,一个连续时间信号完全可以用该信号 在等时间间隔点上的值或样本来表示,并且可以用这 些样本值把该信号全部恢复出来。 ÷听起来有点不可思议,其原理来自于采样定理。 采样的概念使人们找到了这样一种方法:利用离散时 间系统技术来实现连续时间系统并处理连续时间信 号,可以利用采样先把一个连续时间信号进行变换为 一个离散时间信号,再用一个离散时间系统将该离散 信号处理以后,再把它变换回到连续时间中来
7.0 引言 在一定条件下,一个连续时间信号完全可以用该信号 在等时间间隔点上的值或样本来表示,并且可以用这 些样本值把该信号全部恢复出来。 听起来有点不可思议,其原理来自于采样定理。 采样的概念使人们找到了这样一种方法:利用离散时 间系统技术来实现连续时间系统并处理连续时间信 号,可以利用采样先把一个连续时间信号进行变换为 一个离散时间信号,再用一个离散时间系统将该离散 信号处理以后,再把它变换回到连续时间中来

7.0引言 冬采样(柚样):用离散化的一组样本值 表示连续函数的过程或方法。 “采样定理”告诉我们:在一定条件下,一个连 续时间信号或离散序列均可唯一地用其等间 隔的样本值来表示,这种表示是完全和充分 的。 第7章采样 6
第7章 采样 6 7.0 引言 采样(抽样):用离散化的一组样本值 表示连续函数的过程或方法。 “采样定理”告诉我们:在一定条件下,一个连 续时间信号或离散序列均可唯一地用其等间 隔的样本值来表示,这种表示是完全和充分 的
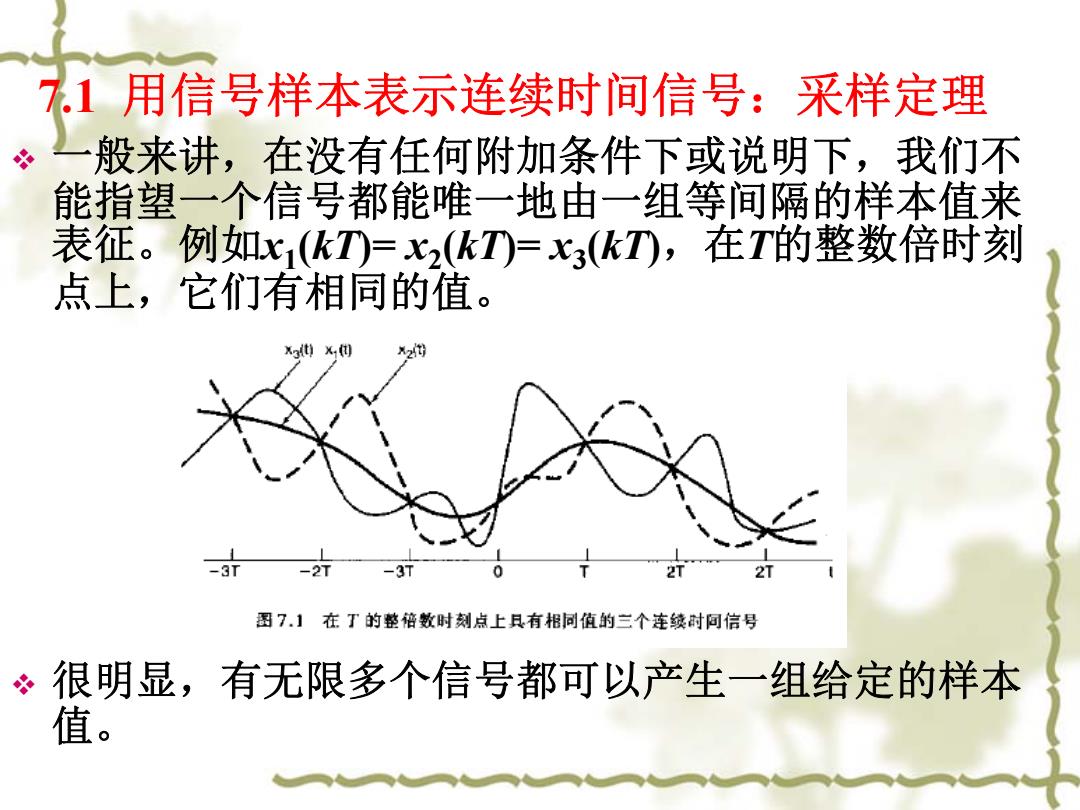
7.1用信号样本表示连续时间信号:采样定理 必 般来讲,在没有任何附加条件下或说明下,我们不 能指望一个信号都能唯一地由一组等间隔的样本值来 表征。例如x1(kT=x2(kTD=3(kT,在T的整数倍时刻 点上,它们有相同的值。 -3 -21 图7.】在丁的整倍数时刻点上具有相同值的三个连续时同信号 很明显,有无限多个信号都可以产生一组给定的样本 值
7.1 用信号样本表示连续时间信号:采样定理 一般来讲,在没有任何附加条件下或说明下,我们不 能指望一个信号都能唯一地由一组等间隔的样本值来 表征。例如x 1 (kT)= x2 (kT)= x3 (kT),在T的整数倍时刻 点上,它们有相同的值。 很明显,有无限多个信号都可以产生一组给定的样本 值

然而,将会看到,如果一个信号是带限的(即它的傅 里叶变换在某一有限频带以外均为零),并且它的样 本取得足够密的话(样本数>ω。,相对于信号中的最 高频率而言),那么这些样本值就能唯一地用来表征 这一信号,并且能从这些样本中把信号完全恢复出 来。这一结果就是采样定理。 0
然而,将会看到,如果一个信号是带限的(即它的傅 里叶变换在某一有限频带以外均为零),并且它的样 本取得足够密的话(样本数>> ,相对于信号中的最 高频率而言),那么这些样本值就能唯一地用来表征 这一信号,并且能从这些样本中把信号完全恢复出 来。这一结果就是采样定理。 0 ω ωc ωc

7.1用信号样本表示连续时间信号:采样定理 ?怎样得到一个连续时间 信号x()的样本值 {x(nT),n=0,±1,±2,…} 答案:冲激串采样。 第7章采样 9
第7章 采样 9 7.1 用信号样本表示连续时间信号:采样定理 ?怎样得到一个连续时间 信号x(t)的样本值 { ( ), 0, 1, 2, } x nT n = ±± 答案:冲激串采样
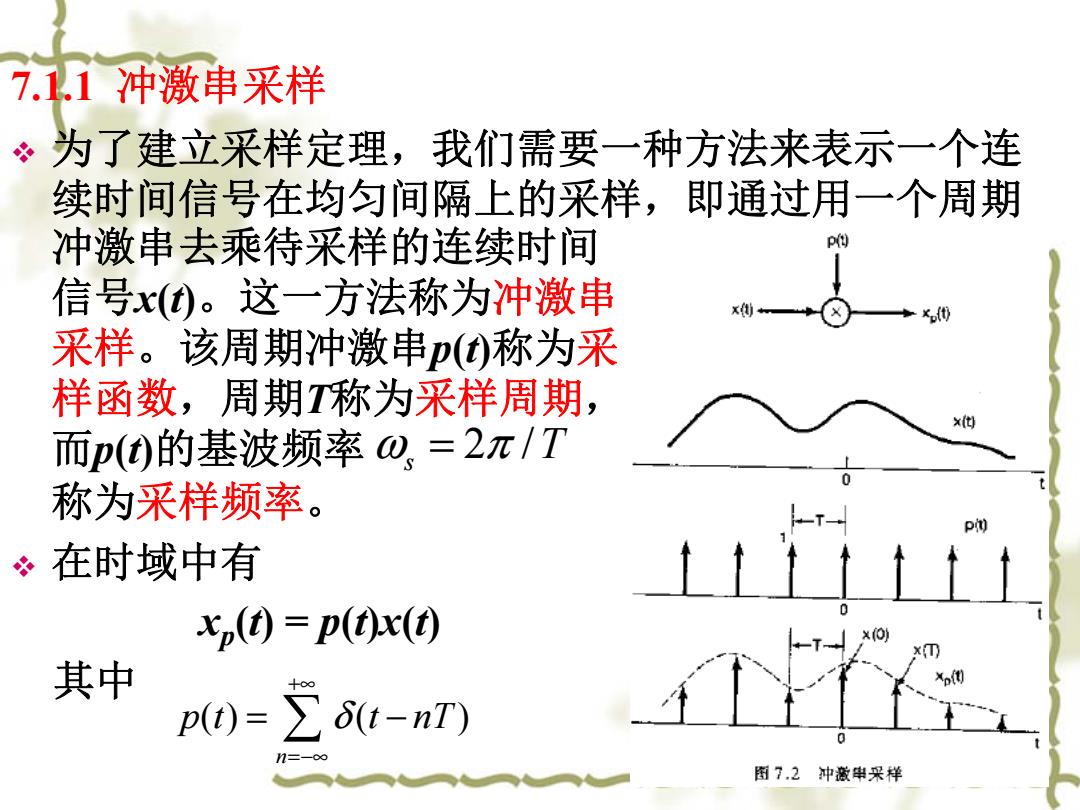
7.1.1冲激串采样 为了建立采样定理,我们需要一种方法来表示一个连 续时间信号在均匀间隔上的采样,即通过用一个周期 冲激串去乘待采样的连续时间 p 信号x()。这一方法称为冲激串 采样。该周期冲激串p()称为采 样函数,周期称为采样周期, ×他 而p()的基波频率⊙,=2π/T 称为采样频率。 ÷在时域中有 xp(④=p()x(t) 其中 p()=∑6t-nT) n=-00 图7,2冲藏串采样
7.1.1 冲激串采样 为了建立采样定理,我们需要一种方法来表示一个连 续时间信号在均匀间隔上的采样,即通过用一个周期 冲激串去乘待采样的连续时间 信号x (t)。这一方法称为冲激串 采样。该周期冲激串p (t)称为采 样函数,周期T称为采样周期, 而p (t)的基波频率 称为采样频率。 在时域中有 xp (t) = p(t)x(t) 其中 2 / ω π s = T () ( ) n p t t nT δ +∞ =−∞ = −

由在1.4.2节曾讨论过的单位冲激函数的性质有: x(t)8(t-t)=x(to)8(t-to) 于是有 ●● x,(t)=∑x()t-nT)=∑x(nT)6t-nT) 1=-co n=-00 可见x,)本身就是一个冲激串,其冲激的幅度等于x() 在以T为间隔处的样本值。 由傅里叶变换的相乘性质知道: X,U@=2元[XUo)*PUw]
由在1.4.2节曾讨论过的单位冲激函数的性质有: 于是有 可见xp ( t)本身就是一个冲激串,其冲激的幅度等于 x ( t) 在以 T为间隔处的样本值。 由傅里叶变换的相乘性质知道: 00 0 xt t t xt t t () ( ) ( ) ( ) δ δ −= − () () ( ) ( ) ( ) p n n x t x t t nT x nT t nT δ δ +∞ +∞ =−∞ =−∞ = −= − 1 ( ) [ ( ) ( )] 2 X p jω ωω X j P j π = ∗
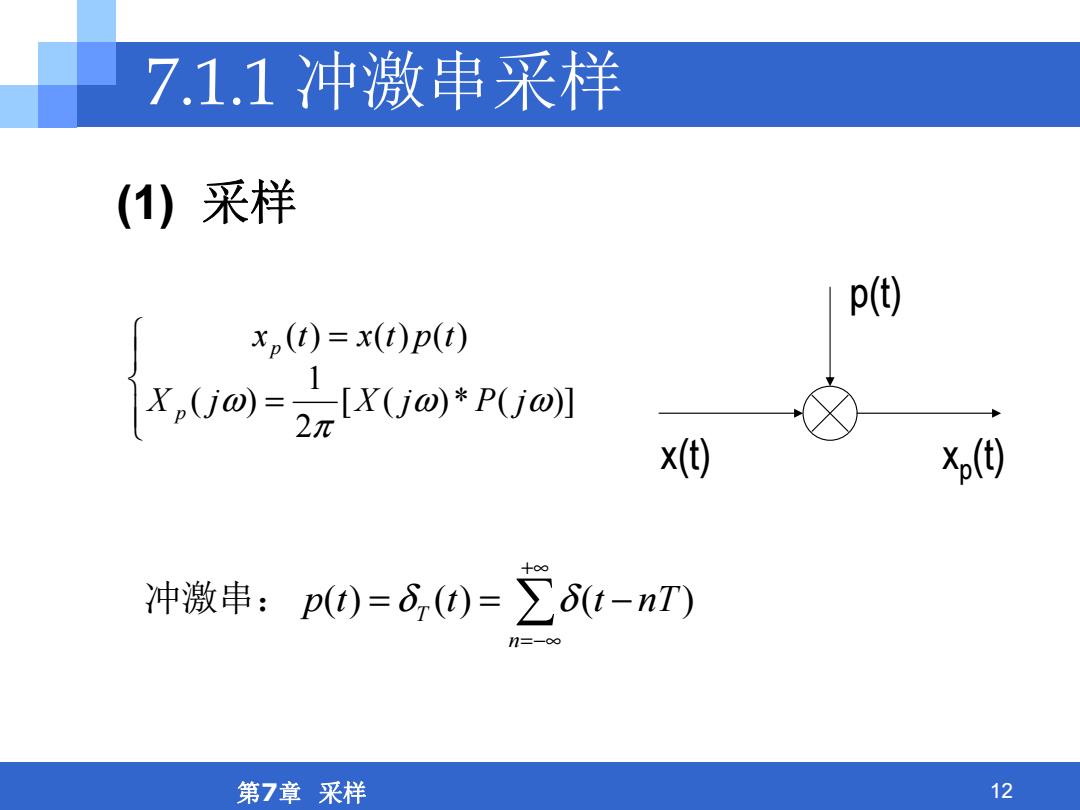
7.1.1冲激串采样 (1)采样 p(t) x,(t)=x(t)p(t) x,Uo=2zXUoPUo1 x(t) 仞 冲激串:p(0=6,()=∑6t-nT) 1=-o 第7章采样 12
第7章 采样 12 7.1.1 冲激串采样 = = )](*)([ 21 )( )()()( ωω π ω jPjXjX tptxtx p p x(t) p(t) xp (t) +∞ =−∞ −== n 冲激串: T δδ nTtttp )()()( (1) 采样