
第4章连续时间傅里叶变换 The Continuous-time Fourier Transform
第4章 连续时间傅里叶变换 The Continuous-time Fourier Transform

重点、难点内容(10学时) 冬FT定义、收敛性、简单信号的FT与逆FT; 周期信号的FT; 冬FT的性质(9个); 冬FT的应用。 第4章连续时间傅里叶变换 2
第4章连续时间傅里叶变换 2 重点、难点内容(10学时) FT定义、收敛性、简单信号的FT与逆FT; 周期信号的FT; FT的性质(9个); FT的应用

学习目标 冬掌握傅里叶变换定义及其基本性质; 牢记常用典型信号的傅里叶变换; 冬掌握求解信号傅里叶变换(正变换和反变换)的基 本方法; 掌握运用傅里叶变换分析LTI系统的方法。 第4章连续时间傅里叶变换 3
第4章连续时间傅里叶变换 3 学习目标 掌握傅里叶变换定义及其基本性质; 牢记常用典型信号的傅里叶变换; 掌握求解信号傅里叶变换(正变换和反变换)的基 本方法; 掌握运用傅里叶变换分析LTI系统的方法

4.0引言 ⑧在第三章我们建立了周期信号作为复指数信号线性 组合的表示,同时,也看到了这一表示是如何来描 述LTI系统对这些信号的响应(作用)效果的, 在本章及下一章,我们将把这些概念推广应用到非 周期信号中去。对周期信号而言,这些复指数基本 信号构造单元全是成谐波的;而对非周期信号,它 们则是在频率上无限小地靠近的。因此这种线性组 合所表示的形式是一个积分,而不是求和。在这种 表示中所得到的系数谱称为傅里叶变换
4.0 引言 在第三章我们建立了周期信号作为复指数信号线性 组合的表示,同时,也看到了这一表示是如何来描 述LTI系统对这些信号的响应(作用)效果的, 在本章及下一章,我们将把这些概念推广应用到非 周期信号中去。对周期信号而言,这些复指数基本 信号构造单元全是成谐波的;而对非周期信号,它 们则是在频率上无限小地靠近的。因此这种线性组 合所表示的形式是一个积分,而不是求和。在这种 表示中所得到的系数谱称为傅里叶变换

4.0引言 傅里叶在把傅里叶级数推广到傅里叶积分的研究 中基于如下的方法: 把非周期函数看作一个周期函数在周 期趋于无穷大时的极限。 ·本章的地位:形成连续时间信号与系统 频域法的基础。 第4章连续时间傅里叶变换 5
第4章连续时间傅里叶变换 5 4.0 引言 傅里叶在把傅里叶级数推广到傅里叶积分的研究 中基于如下的方法: • 本章的地位:形成连续时间信号与系统 频域法的基础。 把非周期函数看作一个周期函数在周 期趋于无穷大时的极限
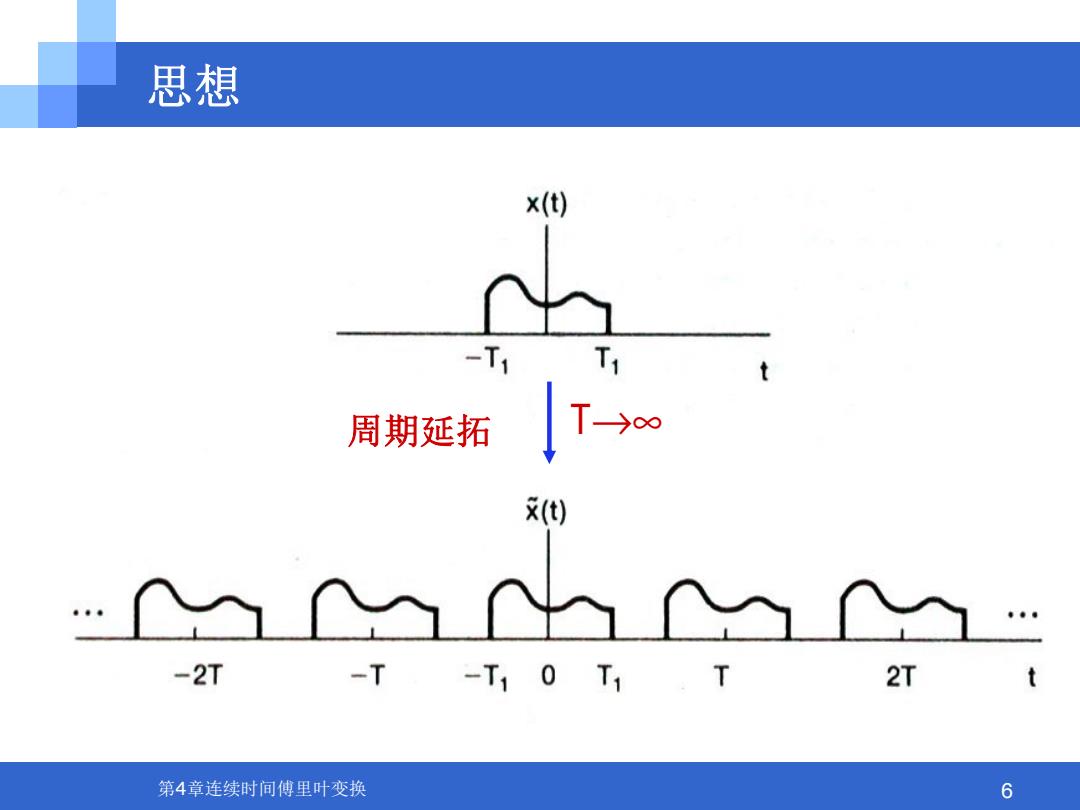
思想 x(t) -Ti T1 周期延拓 - (t) -2T -T -T10T1.T 2T t 第4章连续时间傅里叶变换 6
第4章连续时间傅里叶变换 6 思想 周期延拓 T→∞

在一个周期信号的傅里叶级数表示中,当周期增加 时,基波频率就减小,成谐波关系的各分量在频率 上愈趋靠近。当周期变成无穷大时,这些频率分量 就形成了一个连续域,从而傅里叶级数的求和就变 成了一个积分。 ·傅立叶认为,一个非周期信号能够看成是周期无限 长的周期信号
在一个周期信号的傅里叶级数表示中,当周期增加 时,基波频率就减小,成谐波关系的各分量在频率 上愈趋靠近。当周期变成无穷大时,这些频率分量 就形成了一个连续域,从而傅里叶级数的求和就变 成了一个积分。 傅立叶认为,一个非周期信号能够看成是周期无限 长的周期信号

4.1非周期信号的表示:连续时间傅里叶变换(CFT) The Continuous-time Fourier Transform 4.1.1非周期信号傅里叶变换表示的导出 第4章连续时间傅里叶变换 8
第4章连续时间傅里叶变换 8 4.1 非周期信号的表示:连续时间傅里叶变换(CFT) 4.1.1非周期信号傅里叶变换表示的导出 The Continuous-time Fourier Transform

4.1.1非周期信号傅里叶变换的导出 我们先看例3.5中所研究过的连续时间周期方波,从 它的傅里叶级数入手: 1,l4< 0,T<t<T/2 以周期T周期性重复 0) …] -2T -T z13 2T 图4,1连续时间周期方波信号
4.1.1 非周期信号傅里叶变换的导出 我们先看例3.5中所研究过的连续时间周期方波,从 它的傅里叶级数入手: 以周期 T周期性重复 1 1 1, ( ) 0, / 2 t T x t T tT < = < <

⑧该方波信号的傅里叶级数系数是 2sin(kaT) ax= kaT 理解上式的一种方法是把它当作一个包络函数在每 一个基波频率w整数倍的点上的样本,即 Tak 2sin @T 0 0=k0
该方波信号的傅里叶级数系数 a k 是 理解上式的一种方法是把它当作一个包络函数在每 一个基波频率 ω 0整数倍的点上的样本,即 0 1 0 2sin( ) k k T a k T ω ω = 1 0 2sin k T Ta k ω ω ω ω = =