
第5章离散时间傅里叶变换 The discrete-time Fourier Transform
第5章 离散时间傅里叶变换 The discrete-time Fourier Transform

主要内容、重点(4学时) 冬主要内容 >离散傅立叶变换的定义、性质、应用 冬重点 >离散傅立叶变换的定义 作业 5.232.18 2.19(用本章知识重做) 第5章离散时间傅里叶变换 2
第5章离散时间傅里叶变换 2 主要内容、重点(4学时) 主要内容 离散傅立叶变换的定义、性质、应用 重点 离散傅立叶变换的定义 作业 5.23 2.18 2.19(用本章知识重做)

注释: √CFS(the Continuous-time Fourier Series):连续 时间傅立叶级数 √DFS(the Discrete--time Fourier Series):离散时 间傅立叶级数 *CFT the Continuous -Time Fourier Transforms):连续时间傅立叶变换 DFT the Discrete-Time Fourier Transforms ) 离散时间傅立叶变换 第5章离散时间傅里叶变换 3
第5章离散时间傅里叶变换 3 注释: CFS ( the Continuous-time Fourier Series ): 连续 时间傅立叶级数 DFS ( the Discrete-time Fourier Series ): 离散时 间傅立叶级数 CFT ( the Continuous -Time Fourier Transforms ): 连续时间傅立叶变换 DFT ( the Discrete -Time Fourier Transforms ): 离散时间傅立叶变换

5.0引言 。通过本章的学习,我们将建立完整的傅里叶分析方 法一连续时间与离散时间。 在3.6节,离散时间周期信号的傅里叶级数表示是 个有限项级数。 ·与连续时间情况相比,一个非周期信号的离散时间 傅里叶变换总是周期的,且周期为2π
5.0 引言 通过本章的学习,我们将建立完整的傅里叶分析方 法——连续时间与离散时间。 在3.6节,离散时间周期信号的傅里叶级数表示是一 个有限项级数。 与连续时间情况相比,一个非周期信号的离散时间 傅里叶变换总是周期的,且周期为2π

5.1非周期信号的表示:离散时间傅里叶变换 5.1.1离散时间傅里叶变换的导出 在4.1节,一个连续时间周期方波的傅里叶级数可以 看作是一个包络函数的采样值,并且随着这个方波 周期的增大,这些样本变得愈来愈密。即如何从一 个周期信号获得非周期信号,将连续时间周期信号 的周期无限增大,从而傅里叶级数收敛为连续时间 非周期信号的傅里叶变换。 依照相同的思路,对离散时间非周期序列,为了建 立它的傅里叶变换,将采样与连续时间情况下完全 类似的步骤进行
5.1 非周期信号的表示:离散时间傅里叶变换 5.1.1 离散时间傅里叶变换的导出 在4.1节,一个连续时间周期方波的傅里叶级数可以 看作是一个包络函数的采样值,并且随着这个方波 周期的增大,这些样本变得愈来愈密。即如何从一 个周期信号获得非周期信号,将连续时间周期信号 的周期无限增大,从而傅里叶级数收敛为连续时间 非周期信号的傅里叶变换。 依照相同的思路,对离散时间非周期序列,为了建 立它的傅里叶变换,将采样与连续时间情况下完全 类似的步骤进行

5.1非周期信号的表示:离散时间傅里叶变换 5.1.1离散时间傅里叶变换(DFT) ()傅里级数(周期信号) [n]=∑ae2rwn k= ak= Nne-xiN n= 第5章离散时间傅里叶变换 6
第5章离散时间傅里叶变换 6 5.1非周期信号的表示:离散时间傅里叶变换 (1) 傅里级数 (周期信号) = = = − = Nn nNjk k Nk nNjk k enx N a eanx )/2( )/2( ][ 1 ~ ][ ~ π π 5.1.1 离散时间傅里叶变换(DFT)

傅里级数(周期信号) [n] m -N -N0N2 N n ak 第5章离散时间傅里叶变换 7
第5章离散时间傅里叶变换 7 ][ ~ nx ak N2 傅里级数 (周期信号)
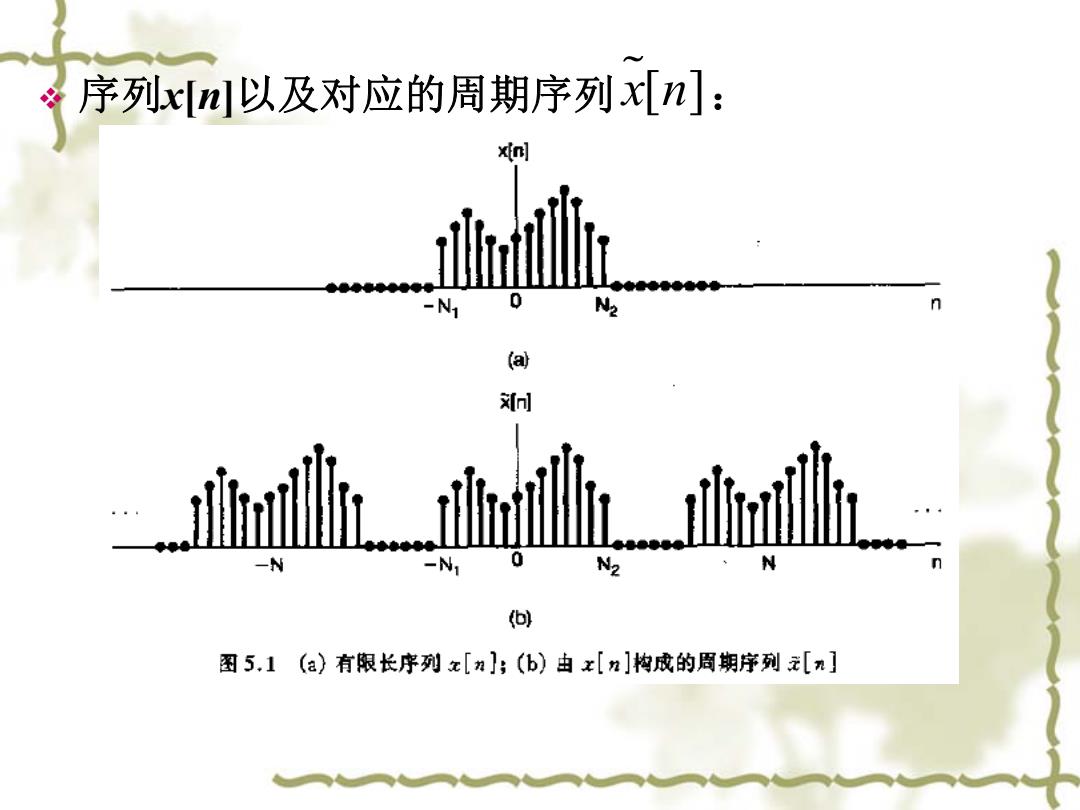
冬序列xm以及对应的周期序列x[n]: n -N1 0 N2 n a (6) 图5,1(a)有限长序列x[n];(b)由x[n]构成的周期序列[元]
序列x[n]以及对应的周期序列 x [ ] n :

。有周期序列的傅里叶级数: xn]=∑a4e2rn &=卡∑ k= n= ÷因为在-N<=n<=N,区间的一个周期上x[n]=x[n] 1 ak= x[n]ek(2π/w)n N n=-N1 =人艺nk2aw N n=-∞
有周期序列的傅里叶级数: 因为在 -N1 − = = = xn xn [] [] = 2 1 (2 / ) (2 / ) 1 [ ] 1 [ ] N jk Nn k n N jk Nn n a xne N xne N π π − =− +∞ − =−∞ = =

现定义函数 X(eo)=∑x[n]em n=-00 即: a) 又因为1/W=o,/2π m=↓∑X(eka)ckaw N kNz ∑Xem)ea"a, 2元k=
现定义函数 即: 又因为 ( ) [] j j n n X e xne ω ω +∞ − =−∞ = 0 1 ( ) jk k a Xe N ω = 0 1/ /2 N =ω π 0 0 0 0 0 1 [] ( ) 1 ( ) 2 jk jk n k N jk jk n k N xn X e e N Xe e ω ω ω ω ω π = = = =