
第3章周期信号的 傅里叶级数表示
第 3 章 周期信号的 傅里叶级数表示

重点、难点内容 LTI系统对复指数信号的响应 >特征函数、特征值 傅立叶级数变换对定义式 连续时间傅里叶级数性质(7个) 冬傅里叶级数收敛条件 傅里叶级数与LTI系统 第3章周期信号的傅里叶级数表示 2
第3章 周期信号的傅里叶级数表示 2 重点、难点内容 LTI系统对复指数信号的响应 特征函数、特征值 傅立叶级数变换对定义式 连续时间傅里叶级数性质(7个) 傅里叶级数收敛条件 傅里叶级数与LTI系统

学习目标 掌握傅里叶级数展开式 & 掌握周期信号通过LTI系统的分析 方法 第3章周期信号的傅里叶级数表示 3
第3章 周期信号的傅里叶级数表示 3 学习目标 掌握傅里叶级数展开式 掌握周期信号通过LTI系统的分析 方法

3.0引言 第2章所学到的卷积和来表示、分析LTI系统,是基 于将信号表示成一组移位单位脉冲的线性组合。 x[n]=∑x[k]Ln-k] k=-o∞ 和第二章一样,本章我们的讨论的出发点仍是将信号 表示成一组基本信号的线性组合,不过这时的基本信 号是复指数,所得到的表示就是连续时间或离散时间 傅里叶级数和傅里叶变换
3.0 引言 第2章所学到的卷积和来表示、分析LTI系统,是基 于将信号表示成一组移位单位脉冲的线性组合。 和第二章一样,本章我们的讨论的出发点仍是将信号 表示成一组基本信号的线性组合,不过这时的基本信 号是复指数,所得到的表示就是连续时间或离散时间 傅里叶级数和傅里叶变换。 [] [][ ] k xn xk n k δ +∞ =−∞ = −

8同第2章的处理方法一样,那就是:根据叠加性 质,LTI系统对任意一个由这些基本信号线性组合 而成的输入信号的响应就是系统对这些基本信号单 个响应的线性组合。在第2章中,这些单个响应皆 为单位脉冲(冲激)响应的移位。 [n]=∑x[k]hn-k] k=-∞ 心在这一章中,我们将学习到,LTI系统对复指数信 号的响应也具有一种特别简单的形式…
同第 2章的处理方法一样,那就是:根据叠加性 质,LTI系统对任意一个由这些基本信号线性组合 而成的输入信号的响应就是系统对这些基本信号单 个响应的线性组合。在第 2章中,这些单个响应皆 为单位脉冲(冲激)响应的移位。 在这一章中,我们将学习到,LTI系统对复指数信 号的响应也具有一种特别简单的形式…… [] [][ ] k yn xkhn k +∞ =−∞ = −

3.0引言 >时域分析方法的基础: 1.信号在时域的分解。 2.LTI系统满足线性、时不变性。 >从分解信号的角度出发,基本信号单元必须满 足两个要求: 1.本身简单,且LTI系统对它的响应能简便得到 2.具有普遍性,能够用以构成相当广泛的信号 第3章周期信号的傅里叶级数表示 6
第3章 周期信号的傅里叶级数表示 6 3.0 引言 时域分析方法的基础: 1. 信号在时域的分解。 2. LTI系统满足线性、时不变性。 2.具有普遍性,能够用以构成相当广泛的信号 1.本身简单,且LTI系统对它的响应能简便得到 从分解信号的角度出发,基本信号单元必须满 足两个要求:

3.1历史回顾 。傅里叶分析方法的建立有着一段漫长的历史。最早 出现在古巴比伦时代,利用“三角函数和”(也就是 成谐波关系的正弦和余弦函数或周期复指数函数的 和)的概念,来预测天体运动。以及后来的古希腊 的占星学家也利用这一想法。因为太阳系的行星运 动是周期性的。 近代,这方面的研究始于瑞士数学家欧拉,他在 1729年解运算行星运行轨道时,得出了这方面的一 些结果。在1748年,欧拉在振动弦的研究工作中, 得出了一个重要的结论
3.1 历史回顾 傅里叶分析方法的建立有着一段漫长的历史。最早 出现在古巴比伦时代,利用“三角函数和”(也就是 成谐波关系的正弦和余弦函数或周期复指数函数的 和)的概念,来预测天体运动。以及后来的古希腊 的占星学家也利用这一想法。因为太阳系的行星运 动是周期性的。 近代,这方面的研究始于瑞士数学家欧拉,他在 1729年解运算行星运行轨道时,得出了这方面的一 些结果。在1748年,欧拉在振动弦的研究工作中, 得出了一个重要的结论
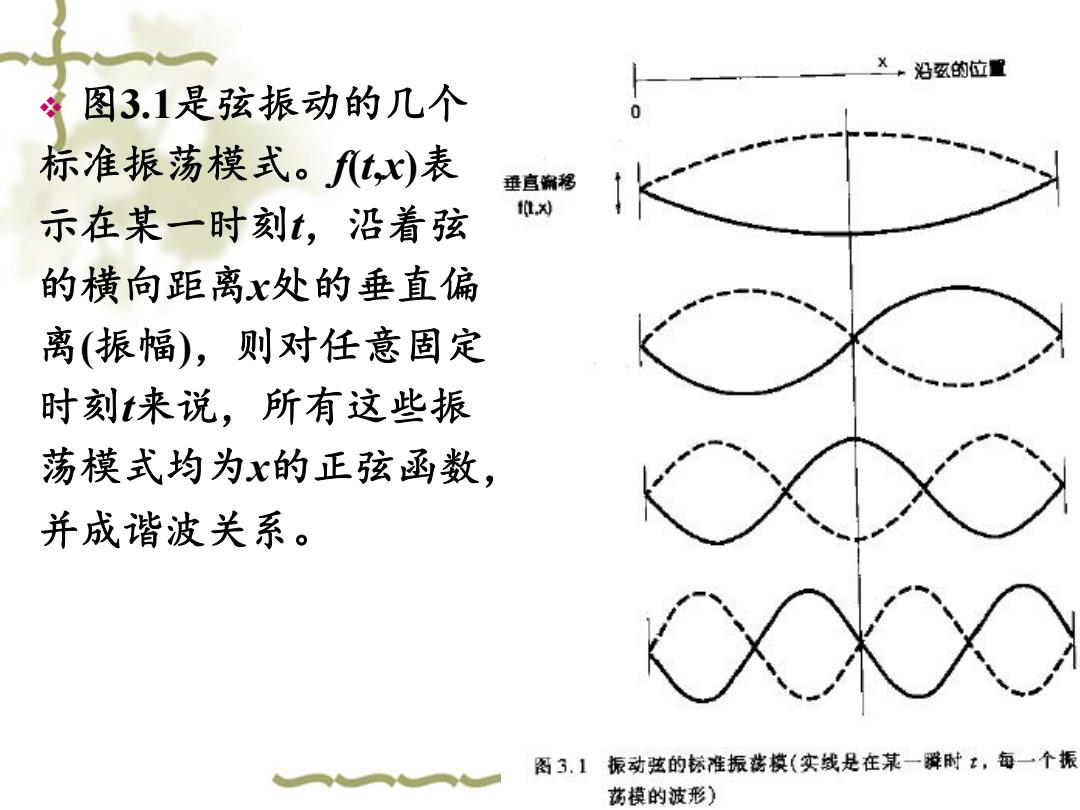
沿致的位置 图3.1是弦振动的几个 标准振荡模式。ft,x)表 垂直锦移 示在某一时刻t,沿着弦 维为 的横向距离x处的垂直偏 离(振幅),则对任意固定 时刻t来说,所有这些振 荡模式均为x的正弦函数, 并成谐波关系。 阁3.1振动弦的标准振酱摸(实线是在某一弹时t,每一个振 荡模的波形)
图3.1是弦振动的几个 标准振荡模式。f(t,x)表 示在某一时刻t,沿着弦 的横向距离x处的垂直偏 离(振幅),则对任意固定 时刻t来说,所有这些振 荡模式均为x的正弦函数, 并成谐波关系

欧拉的结论:如果在某一时刻振动弦的形状是这些 标准振荡模的线性组合,那么在其后任何时刻,振 动弦的形状也都是这些振荡模的线性组合。另外, 欧拉还证明了在该线性组合中,其后面的时间的加 权系数可以直接从前面的加权系数中导出。 。具体地说,就是:如果一个LTI系统的输入可以表 示为周期复指数信号或正弦信号的线性组合,则输 出也一定能表示成这种形式;并且输出线性组合中 的加权系数是直接与输入中对应的系数有关。 伯努利、欧拉,最后都放弃了三角级数的想法。甚 至拉格朗日在1759年还曾强烈批评使用三角级数来 研究弦振动的想法
欧拉的结论:如果在某一时刻振动弦的形状是这些 标准振荡模的线性组合,那么在其后任何时刻,振 动弦的形状也都是这些振荡模的线性组合。另外, 欧拉还证明了在该线性组合中,其后面的时间的加 权系数可以直接从前面的加权系数中导出。 具体地说,就是:如果一个LTI系统的输入可以表 示为周期复指数信号或正弦信号的线性组合,则输 出也一定能表示成这种形式;并且输出线性组合中 的加权系数是直接与输入中对应的系数有关。 伯努利、欧拉,最后都放弃了三角级数的想法。甚 至拉格朗日在1759年还曾强烈批评使用三角级数来 研究弦振动的想法

傅里叶 加入了这场三角级数的论战中 1807年 傅里叶向巴黎科学院递交了《热 的传播》 论文,在研究热的传播和扩散现 象时, 他发现表示一个物体的温度分布 时,其解函数可以由三角函数的级数形式表示。他 断言:“任何”周期信号都可以用成谐波关系的正弦 函数来表示?! 评审《热的传播》论文,4名著名的数学家,其中3 位即拉克劳克斯、孟济、拉普拉斯赞成发表傅里叶 的论文,但第四位评委拉格朗日仍然顽固地坚持他 50年前就已经提出过的关于拒绝接受三角级数的论 点。由于拉格朗日的强烈反对,这份论文从未公开 露面过,直到1822年《热的分析理论》一书才出现 这一研究成果,并为法兰西研究院所接受
傅里叶 加入了这场三角级数的论战中 1807年, 傅里叶向巴黎科学院递交了《热 的传播》 论文,在研究热的传播和扩散现 象时, 他发现表示一个物体的温度分布 时,其解函数可以由三角函数的级数形式表示。他 断言: “任何 ”周期信号都可以用成谐波关系的正弦 函数来表示?! 评审《热的传播》论文, 4名著名的数学家,其中3 位即拉克劳克斯、孟济、拉普拉斯赞成发表傅里叶 的论文,但第四位评委拉格朗日仍然顽固地坚持他 50年前就已经提出过的关于拒绝接受三角级数的论 点。由于拉格朗日的强烈反对,这份论文从未公开 露面过,直到1822年《热的分析理论》一书才出现 这一研究成果,并为法兰西研究院所接受