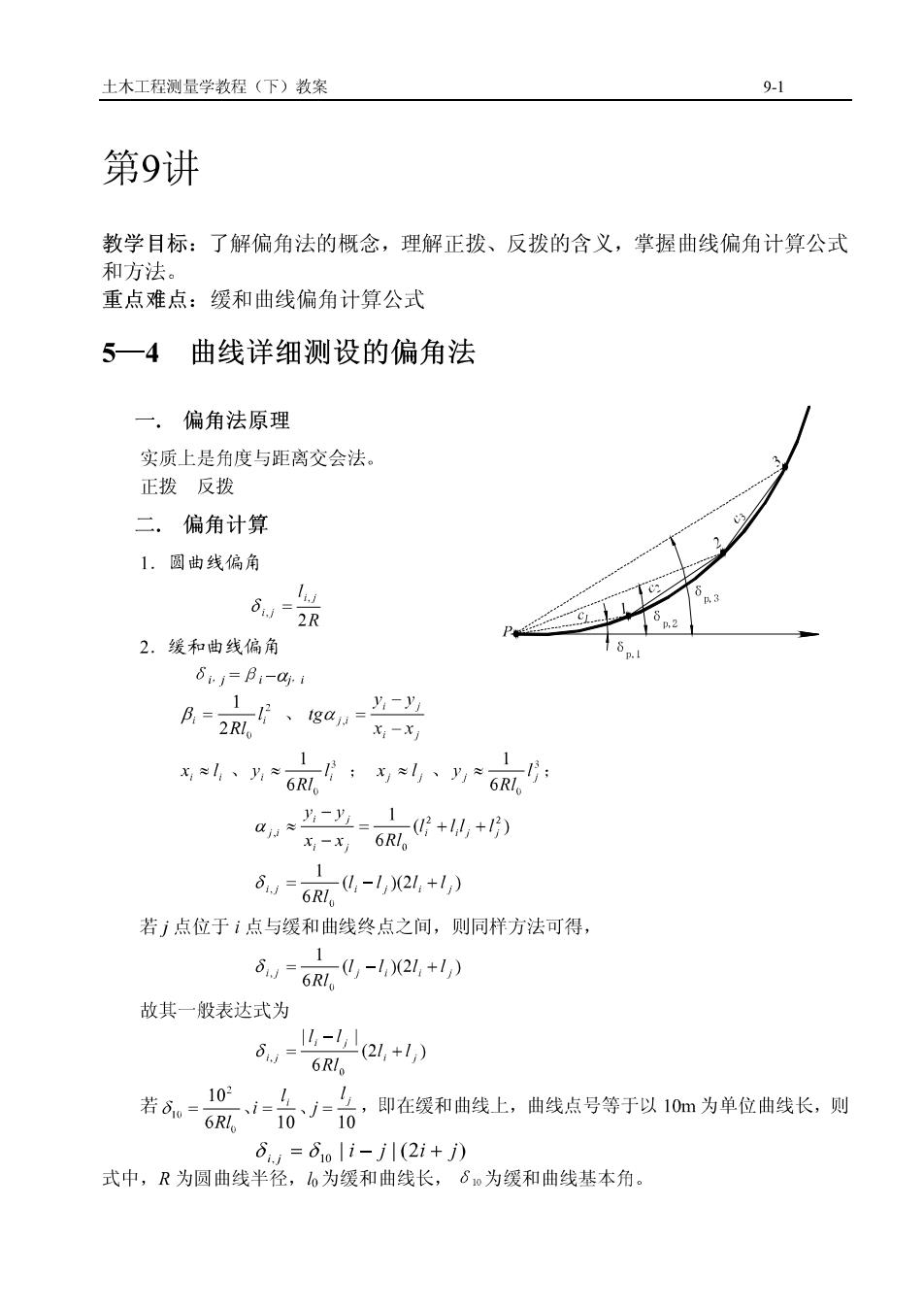
【量学教程(下)教案0-1第9讲教学目标:了解偏角法的概念,理解正拨、反拨的含义,掌握曲线偏角计算公式和方法。重点难点:缓和曲线偏角计算公式5—4曲线详细测设的偏角法偏角法原理.实质上是角度与距离交会法。正拨反拨二.偏角计算1.圆曲线偏角6u2.缓和曲线偏角St.j=βi-dg. 1Y-yB=2R、1gw=--X6R:16Rain-岁=6R(C+1+1)8m =6RI,(-1,)21 +1)若点位于1点与缓和曲线终点之间,则同样方法可得,6. = 6RI,(, -1)(21 +1)故其一般表达式为[4-1) (21. +1)S.6RI.若0%=10元=台、=台,即在级和曲线上,曲线点号等于以10m为单位曲线长,则6Rl.8., =810 li-jl(2i+ j)式中,R为圆曲线半径,l为缓和曲线长,8为缓和曲线基本角
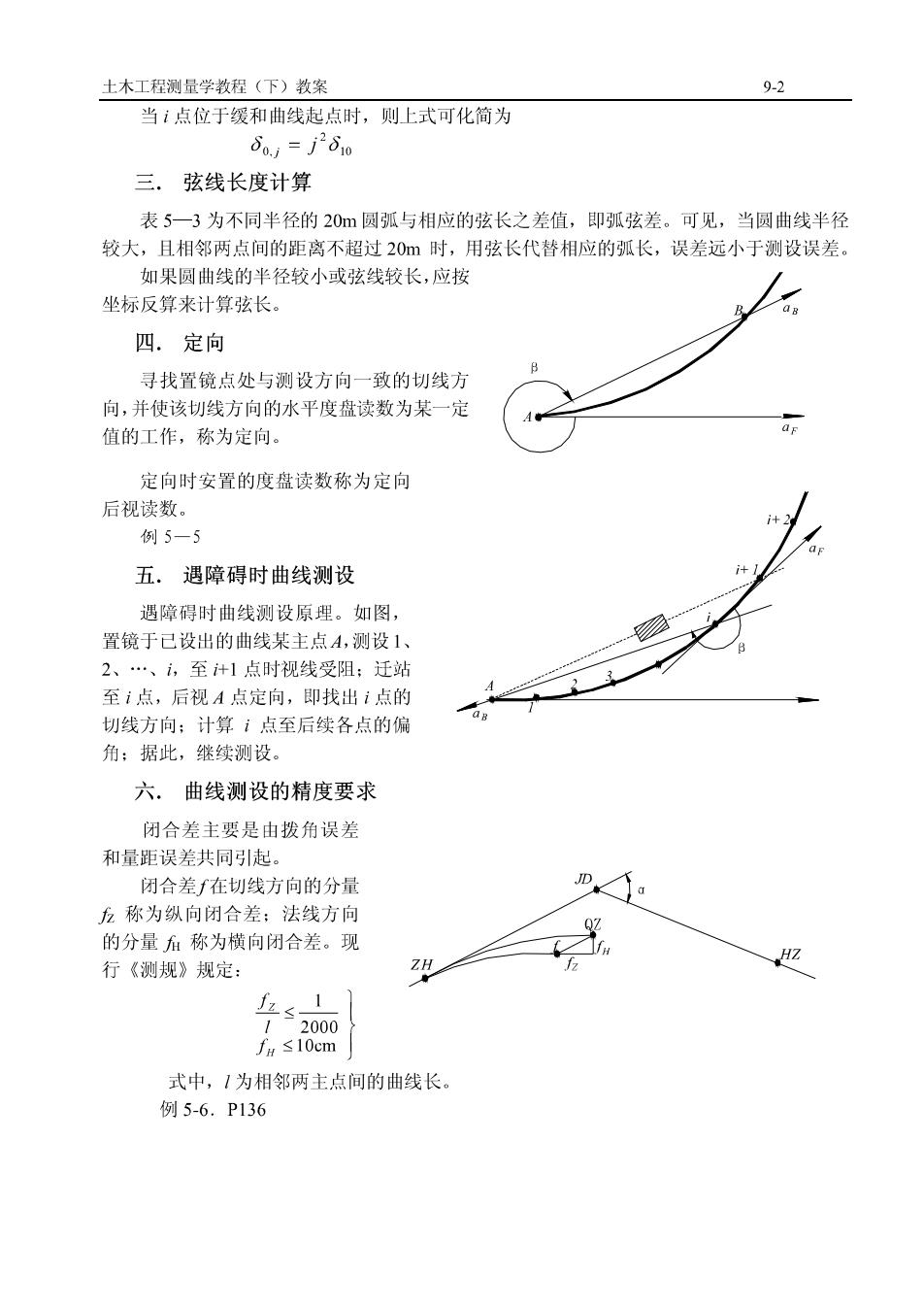
02土木工程测量学教程(下)教案当1点位于缓和曲线起点时,则上式可化简为80.,= j°10三.弦线长度计算表5—3为不同半径的20m圆弧与相应的弦长之差值,即弧弦差。可见,当圆曲线半径较大,且相邻两点间的距离不超过20m时,用弦长代替相应的弧长,误差远小于测设误差。如果圆曲线的半径较小或弦线较长,应按坐标反算来计算弦长。四.定向寻找置镜点处与测设方向一致的切线方向,并使该切线方向的水平度盘读数为某一定aF值的工作,称为定向。定向时安置的度盘读数称为定向后视读数。例 5—5五.遇障碍时曲线测设遇障碍时曲线测设原理。如图,置镜于已设出的曲线某主点A,测设1、2、、i,至计1点时视线受阻;迁站至i点,后视A点定向,即找出i点的-切线方向;计算点至后续各点的偏角;据此,继续测设。六.曲线测设的精度要求闭合差主要是由拨角误差和量距误差共同引起闭合差f在切线方向的分量Dz称为纵向闭合差:法线方向的分量后称为横向闭合差。现HZ行《测规》规定:HJZ0fh≤10cm式中,1为相邻两主点间的曲线长。例5-6.P136

土木工程测量学教程(下)教案9-35一5曲线详细测设的直角坐标法直角坐标法测设曲线原理如图建立平面直角坐标系。待测设的曲线点P点坐标为xp、Vp。测设时,自ZH点于Y轴上丈量xp,得P点;自P点,沿与X轴垂直且指向曲线内侧的方向丈量yp,即得P点。直角坐标法中,坐标系Y轴均选主点的切线,故曲线点的y坐标为相对于切线的支距。因此,直角坐标法也称为切线支距法。曲线点坐标计算直角坐标法所选定的坐标系通常为缓和曲线坐标系,则在该坐标系下,缓和曲线段曲线点坐标的计算公式为缓和曲线方程,圆曲线段曲线点的坐标=Rsina,+my, = R(1-cos α,)+ pJ式中α,=<-K产+β,K为1点的里程,Km为HY里程。R第三节5一6任意点极坐标法测设曲线任意点极坐标法测设曲线的原理任意点极坐标法测设曲线的关键问题是:统一坐标系下的坐标计算;测设数据计算

土木工程测量学教程(下)教案一、坐标计算坐标系的建立主要取决于控制点的情况。如果控制点是为测设曲线而布设的,则坐标系一般采用ZH一XY坐标系统;如果控制点是既有控制点,则控制点所在的坐标系就是统一坐标系,即既有坐标系统。1.ZH一XY测量坐标系下曲线点坐标计算ZH~HY段曲线点的坐标:xa =l -40R?T?13L7:6Rl。-336R7)当曲线右偏时ya坐标为正,左偏时yA坐标为负。HY~YH段曲线点的坐标为:* =Rsinαg +my,=[R(I-cosα,)+p]=K=Km+βe,曲线右偏时ys坐标为正,左偏时ya坐标为负。式中αYH-HZ段曲线点在以HZ点为原点,以HZ点切线为X轴,交点至HZ方向为正向的测量坐标系(HZ—YY)下的坐标为1s40R213171Ve=6Rl。-336R式中,lc为C点到缓和曲线起点的曲线长;按里程增加方向,当曲线右偏时yc坐标为正,左偏时yc坐标为负根据坐标平移、旋转公式,将YH-HZ段曲线点的坐标换算到ZH-XY坐标系下,为[*]-[ cosy sin][*?[-sin y cosyy]+[y hz式中,为两坐标系X轴间的夹角,其与线路转向角的关系是:Y=az 或Y=-αy;xHZ、VHz为 HZ 点在 ZH-XY下的坐标,且为

95测量学教程(下)教案不本XHz =T(I+cOs )YHz =+T sin2.既有坐标系下曲线点坐标计算既有坐标系下曲线点坐标计算分两步:第一步是按前述方法计算出整条曲线在ZH一XY坐标系下的坐标;第二步是根据ZH一XY坐标系与既有坐标系之间的关系,应用坐标平移、旋转公式,将坐标转换到既有坐标系0一XY下。3.控制点的坐标计算若控制点为既有控制点,则其坐标为既有坐标;若控制点是专为测设曲线而建立的,则应测算其坐标。如果置镜点是主点,则称为长弦偏角法。二、测设数据计算测设数据,即置镜点至后视点、曲线点间的坐标方位角和水平距离。根据坐标反算的基本公式计算测设数据,ga,=/-yx,-xDe, = (x, -x)+(y, -)]