
近代物理实验一一物理实验教学中心 实验02电子衍射实验 引言 光的波动性己由光的干涉和衍射实验所证实。上世纪出,爱因斯坦对光电效应现象的研究提出了光子 概念,认为光不仅具有波动性,而且具有粒子性,即具有波粒二象性。 实验目的 1验证电子具有波动性的假设: 2了解电子衍射和电子衍射实验对物理学发展的意义: 3了解电子衍射在研究晶品体结构中的应用。 实验原理 1.电子的波粒二象性 波在传播过程中遇到障碍物时会绕过障碍物继续传播,在经典物理学中称为波的衍射,光在传播过程 表现出波的衍射性,光还表现出干涉和偏振现象,表明光有波动性:光电效应揭示光与物质相互作用时表 现出粒子性,其能量有一个不能连续分割的最小单元,即普朗克1900年首先作为一个基本假设提出来的 普朗克关系 E=hv E为光子的能量,V为光的频率,为普朗克常数,光具有波被粒二象性。电子在与电膜场相互作用时表现为 粒子性,在另一些相互作用过程中是否会表现出波动性?德布罗意从光的波粒二象性得到启发,在1923 一1924年间提出电子具有波粒二象性的假设, E=ho,p=hk E为电子的能量,p为电子的动量,=2πv为平面波的圆频率,k为平面波的波矢量,方=h/2x 为约化普朗克常数:波矢量的大小与波长入的关系为k=2π/入,币=冰称为德布罗意关系。电子具有波 粒二象性的假设,拉开了量子力学革命的序幕。 电子具有波动性假设的实验验证是电子的晶体衍射实验。电子被电场加速后,电子的动能等于电子的 电荷乘加速电压,即 考虑到高速运动的相对论效应,电子的动量
近代物理实验 —— 物理实验教学中心 实验 02 电子衍射实验 引言 光的波动性已由光的干涉和衍射实验所证实。上世纪出,爱因斯坦对光电效应现象的研究提出了光子 概念,认为光不仅具有波动性,而且具有粒子性,即具有波粒二象性。 实验目的 1 验证电子具有波动性的假设; 2 了解电子衍射和电子衍射实验对物理学发展的意义; 3 了解电子衍射在研究晶体结构中的应用。 实验原理 1. 电子的波粒二象性 波在传播过程中遇到障碍物时会绕过障碍物继续传播,在经典物理学中称为波的衍射,光在传播过程 表现出波的衍射性,光还表现出干涉和偏振现象,表明光有波动性;光电效应揭示光与物质相互作用时表 现出粒子性,其能量有一个不能连续分割的最小单元,即普朗克 1900 年首先作为一个基本假设提出来的 普朗克关系 hvE E 为光子的能量,v 为光的频率,h 为普朗克常数,光具有波粒二象性。电子在与电磁场相互作用时表现为 粒子性,在另一些相互作用过程中是否会表现出波动性?德布罗意从光的波粒二象性得到启发,在 1923 -1924 年间提出电子具有波粒二象性的假设, kpE , E 为电子的能量, p 为电子的动量, 2 v 为平面波的圆频率,k 为平面波的波矢量, h 2/ 为约化普朗克常数;波矢量的大小与波长λ的关系为 k /2 , p k 称为德布罗意关系。电子具有波 粒二象性的假设,拉开了量子力学革命的序幕。 电子具有波动性假设的实验验证是电子的晶体衍射实验。电子被电场加速后,电子的动能等于电子的 电荷乘加速电压,即 k eVE 考虑到高速运动的相对论效应,电子的动量 1

近代物理实验一一物理实验教学中心 p=1E(6.+2mc 由德布罗意关系得 hc 入= 2mcE(1+E/2mc2) 真空中的光速c=299793×10i,电子的静止质量m=0.511×10e1c2,普朗克常数 h=4.13571×10-5e,hc=1.23986x10AeV,当电子所受的加速电压为V伏特,则电子的动能 E=eV,电子的德布罗意波长 (1) 加速电压为100伏特,电子的德布罗意波长为1.225A。要观测到电子波通过光栅的衍射花样,光栅的光 橱常数要做到1A的数量级,这是不可能的。晶体中的原子规则排列起来构成品格,晶格间距在1A的数量 级,要观测电子波的衍射,可用晶体的晶格作为光栅。1927年戴维孙_革末用单晶体做实验,汤姆逊用多 晶体做实验,均发现了电子在晶体上的衍射,实验验证了电子具有波动性的假设。 普朗克因为发现了能量子获得1918年诺贝尔物理学奖:德布罗意提出电子具有波粒二象性的假设 导致薛定谔波动方程的建立,而获得1929年诺贝尔物理学奖:戴维孙和汤姆逊因发现了电子在晶体上的 衍射获得1935年诺贝尔物理学奖。 由于电子具有波粒二象性,其德布意波长可在原子尺寸的数量级以下,而且电子束可以用电场或磁场 来聚焦,用电子束和电子透镜取代光束和光学透镜,发展起分辨本领比光学显微镜高得多的电子显微镜。 2.晶体的电子衍射 晶体对电子的衍射原理与晶体对×射线的衍射原理相同,都遵从劳厄方程,即衍射波相干条件为出射 波矢时与入射波矢量K,之差等于品体倒易矢量R的整数倍 k-k。=nK出 设倒易空间的基矢为ā,b,c,倒易矢品 Kwy ha+kb+Ic 在品体中原子规则样成一层一层的平面,称之为晶面,品格倒易矢量的方向为品面的法线方向,大小为品 2
近代物理实验 —— 物理实验教学中心 )2( 1 2 mcEE c p k 由德布罗意关系得 )2/1(2 2 2 mcEEmc hc k k 真空中的光速 ,电子的静止质量 ,普朗克常数 ,当电子所受的加速电压为 V 伏特,则电子的动能 ,电子的德布罗意波长 c sA o /1099793.2 18 hceVs 15 1023986.1, 6 2 m /10511.0 ceV h eVA o 4 1013571.4 k VeVE o AV V )1089.41( 150 7 (1) 加速电压为 100 伏特,电子的德布罗意波长为 。要观测到电子波通过光栅的衍射花样,光栅的光 栅常数要做到 的数量级,这是不可能的。晶体中的原子规则排列起来构成晶格,晶格间距在 的数量 级,要观测电子波的衍射,可用晶体的晶格作为光栅。1927 年戴维孙_革末用单晶体做实验,汤姆逊用多 晶体做实验,均发现了电子在晶体上的衍射,实验验证了电子具有波动性的假设。 o 225.1 A o 1A o 1A 普朗克因为发现了能量子获得 1918 年诺贝尔物理学奖;德布罗意提出电子具有波粒二象性的假设。 导致薛定谔波动方程的建立,而获得 1929 年诺贝尔物理学奖;戴维孙和汤姆逊因发现了电子在晶体上的 衍射获得 1935 年诺贝尔物理学奖。 由于电子具有波粒二象性,其德布意波长可在原子尺寸的数量级以下,而且电子束可以用电场或磁场 来聚焦,用电子束和电子透镜取代光束和光学透镜,发展起分辨本领比光学显微镜高得多的电子显微镜。 2. 晶体的电子衍射 晶体对电子的衍射原理与晶体对 x 射线的衍射原理相同,都遵从劳厄方程,即衍射波相干条件为出射 波矢时 1 k 与入射波矢量 之差等于晶体倒易矢量 0 k Khkl 的整数倍 Knkk hkl 01 设倒易空间的基矢为 cba , ,倒易矢量 hkl clbkahK 在晶体中原子规则排成一层一层的平面,称之为晶面,晶格倒易矢量的方向为晶面的法线方向,大小为晶 2

近代物理实验一一物理实验教学中心 面间距dw的倒数的2π倍 h,k,1为品面指数(又称密勒指数),它们是品面与品格平移基矢量的品格坐标轴截距的约化整数,品面指 数表示晶品面的取向,用来对晶面进行分类,标定衍射花样。 品格对电子波散射有弹性的,弹性散射波在空间相遇发生干涉形成衍射花样,非弹性散射波则形成衍 射花样的背景村度。入射波与晶格弹性散射,入射波矢量与出射波矢量大小相等,以波矢量大小为半径, 作一个球面,从球心向球面与倒易点阵的交点的射线为波的衍射线,这个球面称为反射球(也称厄瓦尔德 球),见图1所示,图中的格点为晶格的倒易点阵(倒易空间点阵)。 晶格的电子衍射几何以及电子衍射与晶体结构的关系由布拉格定律描述,两层晶面上的原子反射的波 相干加强的条件为 2dw sin0=na 日为衍射角的一半,称为半衍射角。见图2所示,图中的格点为晶格点阵(正空间点阵)。0为衍射级,由 于晶格对波的漫反射引起消光作用,n>1的衍射一般都观测不到。 3.电子衍射花样与晶体结构 晶面间距d侧不能连续变化,只能取某些离散值,例如,对于立方晶系的晶体, du 为晶格常数(晶格平移基矢量的长度),是包含晶体全部对称性的、体积最小的晶体单元一一单胞的一个 棱边的长度,图3为立方晶系的三个布拉菲单胞。立方晶系单胞是立方体,沿k三个方向的棱边长度相 ,的三个品指数只能取整致对于正方品系的品体厅十, h,k三个方向相互垂直。h,k两个方向的棱边长度相等。三个品面指数h,kI只能取整数,dw只能取某些 离散值,按照布拉格定律,只能在某些方向接收到衍射线。做单晶衍射时,在衍射屏或感光胶片上只能看 到点状分布的衍射花样,见图4:做多晶衍射时,由于各个晶粒均匀地随机取向,各晶粒中具有相同晶面 指数的晶面的倒易矢在倒易空间各处均匀分布形成倒易球面,倒易球面与反射球面相交为圆环,衍射线为 反射球的球心到圆环的射线,射线到衍射屏或感光胶片上的投影呈环状衍射花样,见图5
近代物理实验 —— 物理实验教学中心 面间距 的倒数的 dhkl 2 倍 hkl hkl d K 2 , lkh 为晶面指数(又称密勒指数),它们是晶面与晶格平移基矢量的晶格坐标轴截距的约化整数,晶面指 数表示晶面的取向,用来对晶面进行分类,标定衍射花样。 晶格对电子波散射有弹性的,弹性散射波在空间相遇发生干涉形成衍射花样,非弹性散射波则形成衍 射花样的背景衬度。入射波与晶格弹性散射,入射波矢量与出射波矢量大小相等,以波矢量大小为半径, 作一个球面,从球心向球面与倒易点阵的交点的射线为波的衍射线,这个球面称为反射球(也称厄瓦尔德 球),见图 1 所示,图中的格点为晶格的倒易点阵(倒易空间点阵)。 晶格的电子衍射几何以及电子衍射与晶体结构的关系由布拉格定律描述,两层晶面上的原子反射的波 相干加强的条件为 dhkl sin2 n 为衍射角的一半,称为半衍射角。见图 2 所示,图中的格点为晶格点阵(正空间点阵)。o 为衍射级,由 于晶格对波的漫反射引起消光作用, 的衍射一般都观测不到。 n 1 3. 电子衍射花样与晶体结构 晶面间距 不能连续变化,只能取某些离散值,例如,对于立方晶系的晶体, dhkl 222 lkh a dhkl a 为晶格常数(晶格平移基矢量的长度),是包含晶体全部对称性的、体积最小的晶体单元——单胞的一个 棱边的长度,图 3 为立方晶系的三个布拉菲单胞。立方晶系单胞是立方体,沿 hkl 三个方向的棱边长度相 等,hkl 三个晶面指数只能取整数;对于正方晶系的晶体 2 2 2 22 1 c l a kh dhkl h,k,l 三个方向相互垂直。h,k 两个方向的棱边长度相等。三个晶面指数 h,k,l 只能取整数, 只能取某些 离散值,按照布拉格定律,只能在某些方向接收到衍射线。做单晶衍射时,在衍射屏或感光胶片上只能看 到点状分布的衍射花样,见图 4;做多晶衍射时,由于各个晶粒均匀地随机取向,各晶粒中具有相同晶面 指数的晶面的倒易矢在倒易空间各处均匀分布形成倒易球面,倒易球面与反射球面相交为圆环,衍射线为 反射球的球心到圆环的射线,射线到衍射屏或感光胶片上的投影呈环状衍射花样,见图 5。 dhkl 3

近代物理实验一一物理实验教学中心 衍射花样的分布规律由晶体的结构决定,并不是所有满足布拉格定律的晶面都会有衍射线产生,这种 现象称为系统消光。若一个单胞中有个原子,以单胞上一个顶点为坐标原点,单胞上第j个原子的位置 矢量为万,=x,ā+y,万+:c,ā,6,c为晶格点阵的平移基矢量,第j个原子的散射波的振幅为A,∫, 为第j个原子的散射因子,根据劳厄方程,一个单胞中·个原子相干散射的复合波振幅 4=42fe-g=4f,eu」 根据正空间和倒易空间的矢量运算规则,Kw·开=2π(x,+内y,+上,)。复合波振幅可写为 A,A,∑,e,+,上式中的求和与单胞中原子的坐标有关,单胞中n个原子相干散射 的复合被振幅受品体的结构影响,令下w=∑∫2,.则单胞的衍射强度A=AF品, F称为结构因子。 对于底心点阵,单胞中只有一个原子,其坐标为[0,0,0],原子散射因子为厂。,F2=2, 任意品面指数的品面都能产生衍射。 对于底心点阵,单胞中有两个原子,其坐标为[0,0,0]和[1/2,1/2,0],若两个原子为同类原子, 原子散射因子为广。,Fw2=f21+cos(h+k)π], 只有当h,k同为偶数或同为奇数时,F才不为0,山,k一个为偶数另为奇数时,F2为0,出现系统消 对于面心点阵,单胞中有4个原子,其坐标为[0,0,0]和[1/2,0,1/2],[0,1/2,1/2],若4个 原子为同类原子,原子散射因子为f。,F2=f1+cos(h+k+)π】,只有(h+k1)为偶数时,F2不 为0,能产生衍射。 对于面心点阵,单胞中有4个原子,其坐标为[0,0,0]和[1/2,0,1/2],[0,1/2,1/2],若4个 原子为同类原子,原子散射因子为,F2=f[1+cos(h+k)+cos(h+)r+cos(k+)z],只有当 h,k,1同为偶数可同为奇数时,F仙才不为0,能产生衍射。 对于单胞中原子数目较多的品体以及由异类原子所组成的品体,还要引入附加系统消光条件 4.电子衍射花样的指数化 根据系统清光条件,可以确定衍射花样的对应晶面的密勒指数k1,这一步骤称为衍射花样的指数化。 4
近代物理实验 —— 物理实验教学中心 4 衍射花样的分布规律由晶体的结构决定,并不是所有满足布拉格定律的晶面都会有衍射线产生,这种 现象称为系统消光。若一个单胞中有 n 个原子,以单胞上一个顶点为坐标原点,单胞上第 j 个原子的位置 矢量为 , 为晶格点阵的平移基矢量,第 j 个原子的散射波的振幅为 为第 j 个原子的散射因子,根据劳厄方程,一个单胞中 n 个原子相干散射的复合波振幅 。 czbyaxr jjjj n j rkki ja j ef )( 01 cba , n j j ef jja , ffA rki b a jhkl AA A 根据正空间和倒易空间的矢量运算规则, (2 ) jhkl jjj lzkyhxrK 。复合波振幅可写为 ,上式中的求和与单胞中原子的坐标有关,单胞中 n 个原子相干散射 的复合波振幅受晶体的结构影响,令 。则单胞的衍射强度 , 称为结构因子。 n j lzkyhxi b a j jjj efAA (2 ) Fhkl n j Fhkl lzkyhxi j jjj ef (2 ) 2 22 b FAA hkla 对于底心点阵,单胞中只有一个原子,其坐标为[0,0,0],原子散射因子为 fa , , 2 2 hkl a fF 任意晶面指数的晶面都能产生衍射。 对于底心点阵,单胞中有两个原子,其坐标为[0,0,0]和[1/2,1/2,0],若两个原子为同类原子, 原子散射因子为 , 只有当 h,k 同为偶数或同为奇数时, 才不为 0,h,k 一个为偶数另为奇数时, 为 0,出现系统消 光。 af ],)cos(1[ 2 2 hkl a khfF Fhkl 2 Fhkl 对于面心点阵,单胞中有 4 个原子,其坐标为[0,0,0]和[1/2,0,1/2],[0,1/2,1/2],若 4 个 原子为同类原子,原子散射因子为 , 只有(h+k+l)为偶数时, 不 为 0,能产生衍射。 af cos(1[ ],) 2 2 hkl a lkhfF 2 Fhkl 对于面心点阵,单胞中有 4 个原子,其坐标为[0,0,0]和[1/2,0,1/2],[0,1/2,1/2],若 4 个 原子为同类原子,原子散射因子为 , 只有当 h,k,l 同为偶数可同为奇数时, 才不为 0,能产生衍射。 af ,])cos()cos()cos(1[ 2 2 hkl a lklhkhfF Fhkl 对于单胞中原子数目较多的晶体以及由异类原子所组成的晶体,还要引入附加系统消光条件。 4. 电子衍射花样的指数化 根据系统消光条件,可以确定衍射花样的对应晶面的密勒指数 hkl,这一步骤称为衍射花样的指数化

近代物理实验一一物理实验教学中心 对衍射花样指数化,可确定晶体结构,若己知电子波的波长,则可计算晶格常数,若己知晶格常数(由× 射线衍射测定),则可计算电子波的波长,验证德布罗意关系。以简单格子立方品系的多品衍射花样为例, 介绍环状衍射花样的指数化。 对于电子衍射,电子波的波长很短,日角一般只有1°一2°,设衍射环的半径为R,晶体到衔射屏或 感光胶片的距离为L,由图6所示的几何关系可知R/L≈20≈2si0,则布拉格定律为 R=Ln或R=Lg (2) d 式中L入称为仪器常数。g=/2π,电子衍射花样就是品格倒易矢放大L1/2π倍的象。将立方晶系 的品面州便du代入有数定#有及=LH公7成R.以c,品面新版只双数,◆ a m=(+k2+),则各衍射环半径平方的顺序比为R::R.=m:m,:m,:.,按照系统消光 规律,对于简单立方、体心立方和面心立方晶格,半径最小的衍射环对应的密勒指数分别为100、110、111, 这三个密勒指数对应的品面分别是简单立方、体心立方和面心立方晶格中晶面间距最小的品面。这三个晶 格的衍射环半径排列顺序和对应的密勒指数见表1,将衍射环半径的平方比表1对照,一般可确定衍射环 的密勒指数。衍射花样的指数化后,对已知晶格常数的晶体,仪器常数 LA=R-+P (3) 若己知仪器常数,则可计算晶格常数 a-只状, (4) 表1:简单格子立方晶系衍射环的密勒指数 简单立方 体心立方 面心立方 衍射环 序号 hkl m hkl m m/m 100 10 2 3 10 2 200 2 200 41.33
近代物理实验 —— 物理实验教学中心 对衍射花样指数化,可确定晶体结构,若已知电子波的波长,则可计算晶格常数,若已知晶格常数(由 x 射线衍射测定),则可计算电子波的波长,验证德布罗意关系。以简单格子立方晶系的多晶衍射花样为例, 介绍环状衍射花样的指数化。 对于电子衍射,电子波的波长很短, 角一般只有 1°~ 2°,设衍射环的半径为 R,晶体到衍射屏或 感光胶片的距离为 L,由图 6 所示的几何关系可知 LR sin22/ ,则布拉格定律为 gLR d LR hkl 或 1 , (2) 式中 L 称为仪器常数。 Kg hkl 2/ ,电子衍射花样就是晶格倒易矢放大 L 2/ 倍的象。将立方晶系 的晶面间距 代入布拉定律得 dhkl c a L R a lkh LR 2 2 2 2 222 或 。晶面指数 h,k,l 只能取整数,令 ,则各衍射环半径平方的顺序比为 ,按照系统消光 规律,对于简单立方、体心立方和面心立方晶格,半径最小的衍射环对应的密勒指数分别为 100、110、111, 这三个密勒指数对应的晶面分别是简单立方、体心立方和面心立方晶格中晶面间距最小的晶面。这三个晶 格的衍射环半径排列顺序和对应的密勒指数见表 1,将衍射环半径的平方比表 1 对照,一般可确定衍射环 的密勒指数。衍射花样的指数化后,对已知晶格常数的晶体,仪器常数 ) 2 m ( 2 h 2 lk 1 2 2 2 3 2 ::: mRRR 1 mm 32 ::: 222 lkh a RL , (3) 若已知仪器常数,则可计算晶格常数 222 lkh R L a , (4) 表 1:简单格子立方晶系衍射环的密勒指数 简单立方 体心立方 面心立方 衍射环 序号 hkl m 1 l / mm hkl m 1 l / mm hkl m 1 l / mm 1 100 1 1 110 2 1 111 3 1 2 110 2 2 200 4 2 200 4 1.33 5
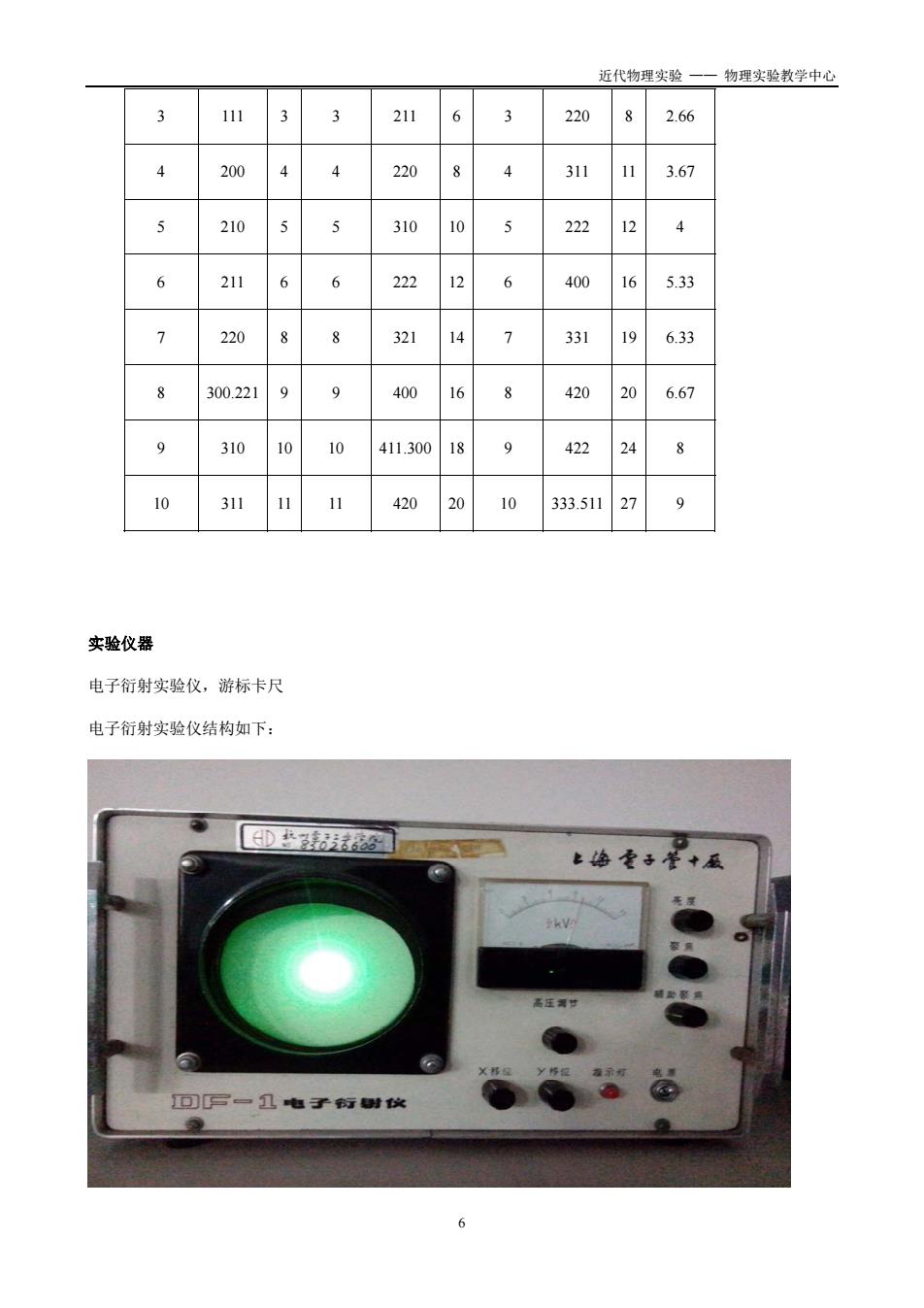
近代物理实验一一物理实验教学中心 211 3 220 2.66 220 311 3.67 210 310 10 222 4 211 22 12 400 6 5.33 20 321 6.33 00.221 400 6 420 6.67 310 10 411.300 18 422 8 10 311 11 420 20 10 333.51127 实验仪器 电子衍射实验仪,游标卡尺 电子衍射实验仪结构如下: 回写一包电子每时仪
近代物理实验 —— 物理实验教学中心 3 111 3 3 211 6 3 220 8 2.66 4 200 4 4 220 8 4 311 11 3.67 5 210 5 5 310 10 5 222 12 4 6 211 6 6 222 12 6 400 16 5.33 7 220 8 8 321 14 7 331 19 6.33 8 300.221 9 9 400 16 8 420 20 6.67 9 310 10 10 411.300 18 9 422 24 8 10 311 11 11 420 20 10 333.511 27 9 实验仪器 电子衍射实验仪,游标卡尺 电子衍射实验仪结构如下: 6

近代物理实验一一物理实验教学中心 电子衍射主要由两部分组成: (1) 电子衍射管 电子衍射管包括3个部分: a电子枪。它由阴极、灯丝、调制极、加速极、聚焦极、辅助聚焦极和xy偏转板等组成 b晶体薄膜样品。 c荧光屏 电子衍射的外壳为玻璃制成,内部抽成高真空。样品周围的玻璃壳部分涂有石墨层,并和荧光屏、样品相 连,接到可调高压直流电源正极,阴极接到负极。 (2)电源部分 加在晶体薄膜和阴极只见到高压6-18KV连续可调,面板上有电压表指示这个高压。灯丝电源为6.3V。阴 极和各组阳极及xy偏转板均另有几组电源供给。本仪器要求薄膜和阴极之间的高压电源有较高的稳定度, 较小的纹波,以保证衍射环的稳定和清晰程度。 实验步骤 1、熟悉仪器及注意事项。 2、先将高压调到最小位置,再开衍射仪电源。 3、调整仪器的聚焦和衍射环位置,调整时将高压调到10kV,亮度适中。 3、调节x和y位置,使屏上出现光点。调节聚焦、辅助聚焦和亮度,出现较为清晰的衍射环。 4、测量衍射环的直接,多次测量去平均值。 5、将电压调到最小后关闭电源。 6、将直径代入公式算出波长和普朗克常数。 注意事项 开机前高压旋钮必须调到最小位置,亮度旋钮调到之间位置
近代物理实验 —— 物理实验教学中心 7 电子衍射主要由两部分组成: (1) 电子衍射管 电子衍射管包括 3 个部分: a 电子枪。它由阴极、灯丝、调制极、加速极、聚焦极、辅助聚焦极和 xy 偏转板等组成 b 晶体薄膜样品。 c 荧光屏 电子衍射的外壳为玻璃制成,内部抽成高真空。样品周围的玻璃壳部分涂有石墨层,并和荧光屏、样品相 连,接到可调高压直流电源正极,阴极接到负极。 (2) 电源部分 加在晶体薄膜和阴极只见到高压 6-18KV 连续可调,面板上有电压表指示这个高压。灯丝电源为 6.3V。阴 极和各组阳极及 xy 偏转板均另有几组电源供给。本仪器要求薄膜和阴极之间的高压电源有较高的稳定度, 较小的纹波,以保证衍射环的稳定和清晰程度。 实验步骤 1、 熟悉仪器及注意事项。 2、 先将高压调到最小位置,再开衍射仪电源。 3、调整仪器的聚焦和衍射环位置,调整时将高压调到 10kv,亮度适中。 3、 调节 x 和 y 位置,使屏上出现光点。调节聚焦、辅助聚焦和亮度,出现较为清晰的衍射环。 4、 测量衍射环的直接,多次测量去平均值。 5、 将电压调到最小后关闭电源。 6、 将直径代入公式算出波长和普朗克常数。 注意事项 开机前高压旋钮必须调到最小位置,亮度旋钮调到之间位置