
第五讲点对称操作、晶系与点群(1)
第五讲 点对称操作、晶系与点群(1)

A Crystal Emerges from a Chaotic Sea of Molecules 504s a 电子衍射©是一种用于材料表征的技术,是将高能电子束照射到样品表面并在探测器上 收集散射电子图像的过程。它起源于1930年代,并被广泛应用于物理学、化学和材料科 学等领域 1.电子衍射原理 电子衍射的原理基于布拉格衍射定律,即晶体中的原子会对入射电子形成衍射,从而产 生干涉条纹的图样。当电子波长与晶格常数相近时,反射会发生共振增强,则可以从试 样表面获取有关晶体结构的信息。 2.电子衍射的特点 与X射线行射不同,电子衍射的波长比X射线短,因此可以提供更高分辨率的数据。此 外,电子具有明显的波粒二象性,其传播路径会遵循通过梳状电场的路径。 3.电子衍射的应用 电子行射广泛应用于物理学、化学和材料科学等领域。例如,在材料科学中,电子衍射 可以用于表征晶体结构、晶格畸变和缺陷等信息;在催化研究中,电子衍射可用于分析 触媒的表面结构

上节课内容 表4.1.1对称元素和对称操作 对称元素符号 对称元素 基本对称操作符号 基本对称操作 E 一 E 恒等操作 C. 旋转轴 c 绕C.轴按逆时针方向转360°/n g 镜面 6 通过镜面反映 对称中心 按对称中心反演 Sn 映轴 S.=oCl 绕S.轴转360°/n,接着按垂直于轴的平面反映 I. 反轴 县=C 绕In轴转360°/n,接着按中心点反演
上节课内容

点对称操作 n=In (iC )Sp=6Cn 1(E,L) 1(亿,C) 2(C2,L2) 2(o,P),m (Oh,Oy,Od) 3(C3,L3) 3(S65,L3) (C31,C32,C33) S6,S62(Cg),S。(0,S6(C32),S65,S6E 35,34 33.32 31.36 4(C4,L4) 4(S43,L4) (C4,C42,C43,C44) S4(49),S42(42),S43(4),S44(E) 6(C6,L6) 6(S35,L6) (C61,C62,C63,C64 S3,S32C32),S3(o),S4C),S5,S3E) C65,C6) 65,64, 63, 62 6, 6
1 (E, L1 ) 2 (C2 , L2 ) 3 (C3 , L3 ) 4 (C4 , L4 ) 6 (C6 , L6 ) 1 (i, C) 2 (σ, P), m 3 (S6 5 , Li 3 ) 4 (S4 3 , Li 4 ) 6 (S3 5 , Li 6 ) (C4 1 , C4 2 , C4 3 , C4 4 ) (C6 1 , C6 2 , C6 3 , C6 4 , C6 5 , C6 6 ) (C3 1 , C3 2 , C3 3 ) n = 1n (iCn ), Sn = σCn (σh , σv , σd ) S6 , S6 2 (C3 ), S6 3 (i), S6 4 (C3 2 ), S6 5 , S6 6 (E) 3 5 , 34 , 33 , 32 , 31 , 36 S3 , S3 2 (C3 2 ), S3 3 (σh ), S3 4 (C3 ), S3 5 , S3 6 (E) 6 5 , 64 , 63 , 62 , 6, 66 S4 (43 ), S4 2 (42 ), S4 3 (4), S4 4 (E) 点对称操作
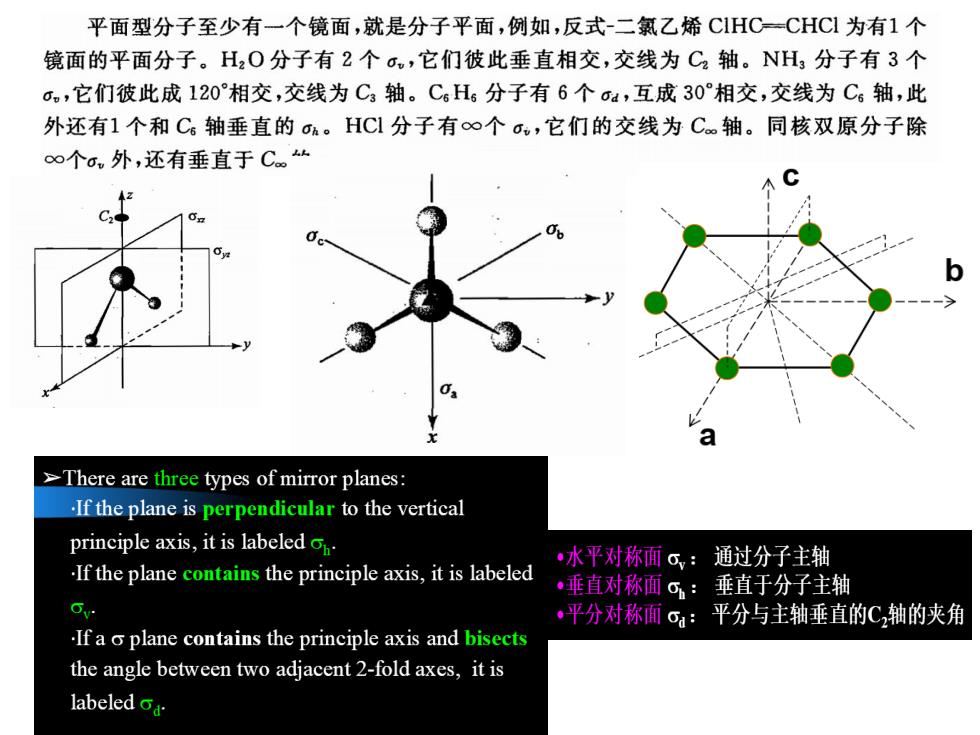
平面型分子至少有一个镜面,就是分子平面,例如,反式-二氯乙烯CIHC=CHCl为有1个 镜面的平面分子。H2O分子有2个o,它们彼此垂直相交,交线为C2轴。NH分子有3个 ,它们彼此成120相交,交线为C轴。C6H6分子有6个04,互成30°相交,交线为C。轴,此 外还有1个和Cs轴垂直的oh。HCl分子有∞个o。,它们的交线为C轴。同核双原分子除 ∞个cm外,还有垂直于C“ >There are three types of mirror planes: .If the plane is perpendicular to the vertical principle axis,it is labeled ·水平对称面c,:通过分子主轴 .If the plane contains the principle axis,it is labeled 垂直对称面σ:垂直于分子主轴 C 平分对称面5a:平分与主轴垂直的C,轴的夹角 .If a o plane contains the principle axis and bisects the angle between two adjacent 2-fold axes,it is labeled oa
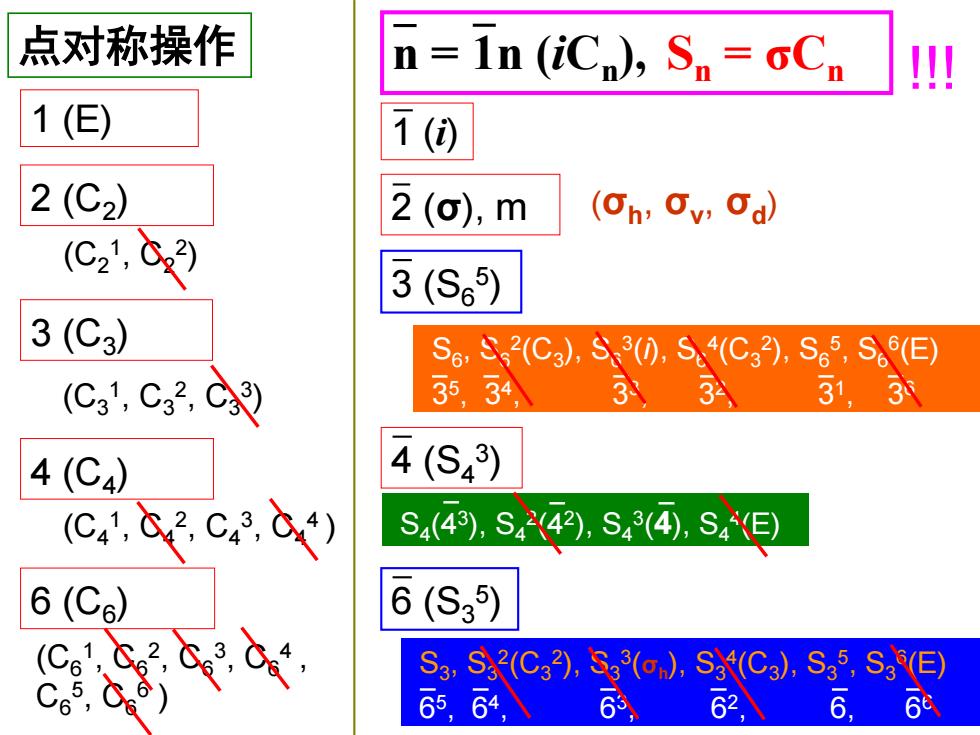
点对称操作 n=In (iC),Sp=6Cn 山 1(E) 1() 2(C2) 2(),m (On,Ov,Od) (C21,6,2) 3(S65) 3(C3) S6,S2(Cg),S30,S(C32),S65,SE) (Cg1,C2,d3 35,34 3 3 31,3 4(C4) 4(S43) C.83.ca8t) S4(43),S442),S43(4),S4) 6(C6) 6(S35) S3.S2(Ca2),S(),Sat(Ca),S5,Sg(E) 65, 64, 6 62, 6,68
1 (E) 2 (C2 ) 3 (C3 ) 4 (C4 ) 6 (C6 ) 1 (i) 2 (σ), m 3 (S6 5 ) 4 (S4 3 ) 6 (S3 5 ) (C4 1 , C4 2 , C4 3 , C4 4 ) (C6 1 , C6 2 , C6 3 , C6 4 , C6 5 , C6 6 ) (C3 1 , C3 2 , C3 3 ) n = 1n (iCn ), Sn = σCn (σh , σv , σd ) S4 (43 ), S4 2 (42 ), S4 3 (4), S4 4 (E) 点对称操作 !!! (C2 1 , C2 2 ) S6 , S6 2 (C3 ), S6 3 (i), S6 4 (C3 2 ), S6 5 , S6 6 (E) 3 5 , 34 , 33 , 32 , 31 , 36 S3 , S3 2 (C3 2 ), S3 3 (σh ), S3 4 (C3 ), S3 5 , S3 6 (E) 6 5 , 64 , 63 , 62 , 6, 66
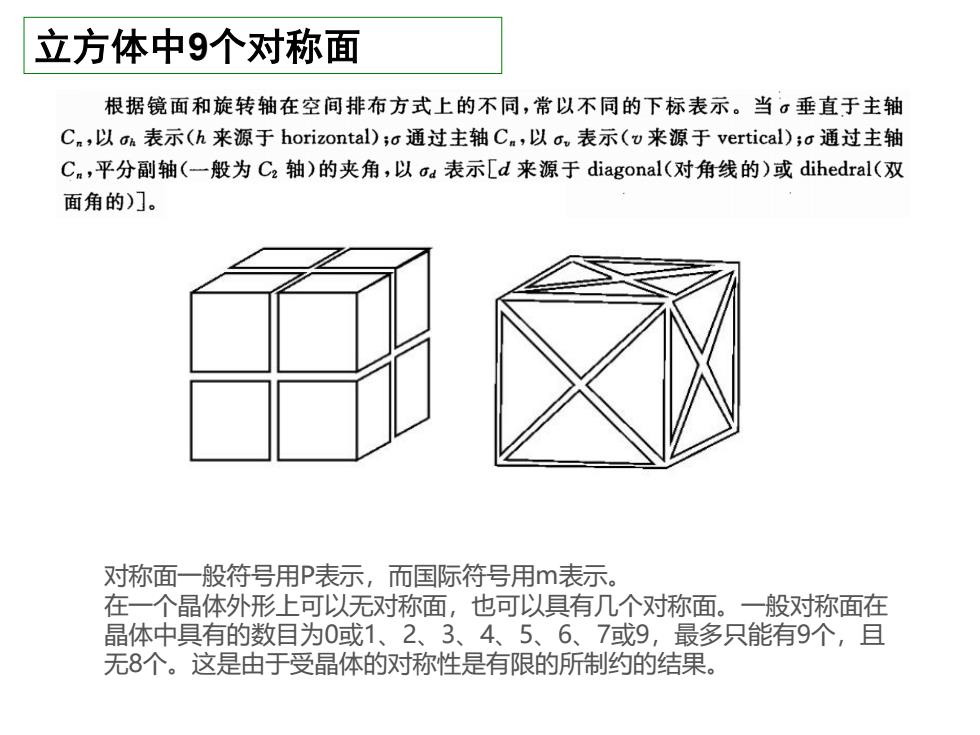
立方体中9个对称面 根据镜面和旋转轴在空间排布方式上的不同,常以不同的下标表示。当。垂直于主轴 Cn,以oa表示(h来源于horizontal);o通过主轴Cn,以o,表示(v来源于vertical);c通过主轴 Cn,平分副轴(一般为Cz轴)的夹角,以oa表示[d来源于diagonal(对角线的)或dihedral(双 面角的)门。 对称面一般符号用P表示,而国际符号用m表示。 在一个晶体外形上可以无对称面,也可以具有几个对称面。一般对称面在 晶体中具有的数目为0或1、2、3、4、5、6、7或9,最多只能有9个,且 无8个。这是由于受晶体的对称性是有限的所制约的结果
立方体中9个对称面 对称面一般符号用P表示,而国际符号用m表示。 在一个晶体外形上可以无对称面,也可以具有几个对称面。一般对称面在 晶体中具有的数目为0或1、2、3、4、5、6、7或9,最多只能有9个,且 无8个。这是由于受晶体的对称性是有限的所制约的结果

对称面在晶体常出现的位置 晶体外形上,对称面与晶体组成要素之间有一定关系,它与晶 面、晶棱及角顶的关系如下: (1)对称面垂直并平分晶面。 (2)对称面通过晶体中心并垂直平分晶棱。 (3)对称面可以平行晶棱。 (4)对称面垂直平分晶面和角顶
对称面在晶体常出现的位置 晶体外形上,对称面与晶体组成要素之间有一定关系,它与晶 面、晶棱及角顶的关系如下: (1)对称面垂直并平分晶面。 (2)对称面通过晶体中心并垂直平分晶棱。 (3)对称面可以平行晶棱。 (4)对称面垂直平分晶面和角顶
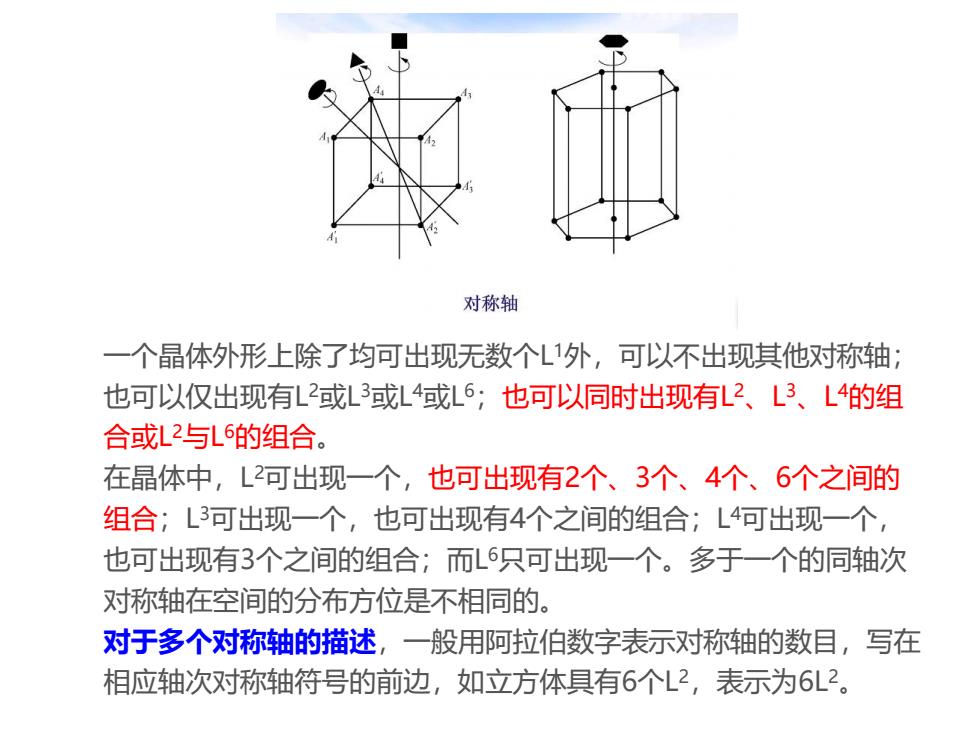
对称轴 一个晶体外形上除了均可出现无数个L1外,可以不出现其他对称轴: 也可以仅出现有L2或L或L4或L6;也可以同时出现有L2、L3、L4的组 合或L2与1的组合。 在晶体中,L2可出现一个,也可出现有2个、3个、4个、6个之间的 组合;L3可出现一个,也可出现有4个之间的组合;L4可出现一个, 也可出现有3个之间的组合;而6只可出现一个。多于一个的同轴次 对称轴在空间的分布方位是不相同的。 对于多个对称轴的描述,一般用阿拉伯数字表示对称轴的数目,写在 相应轴次对称轴符号的前边,如立方体具有6个L2,表示为6L2
一个晶体外形上除了均可出现无数个L 1外,可以不出现其他对称轴; 也可以仅出现有L 2或L 3或L 4或L 6;也可以同时出现有L 2 、L 3 、L 4的组 合或L 2与L 6的组合。 在晶体中,L 2可出现一个,也可出现有2个、3个、4个、6个之间的 组合;L 3可出现一个,也可出现有4个之间的组合;L 4可出现一个, 也可出现有3个之间的组合;而L 6只可出现一个。多于一个的同轴次 对称轴在空间的分布方位是不相同的。 对于多个对称轴的描述,一般用阿拉伯数字表示对称轴的数目,写在 相应轴次对称轴符号的前边,如立方体具有6个L 2,表示为6L2