
第十三讲空间群(4):空间群中的特殊位置 1、二维空间群(全部) 2、空间群国际表中的特殊位置举例分析
第十三讲 空间群(4):空间群中的特殊位置 1、二维空间群(全部) 2、空间群国际表中的特殊位置举例分析

http://img.chem.ucl.ac.uk/sgp/large/sgp.htm https://bruceravel.github.io/demeter/artug/atoms/space.html https://www.ruppweb.org/Xray/comp/space_instr.htm
http://img.chem.ucl.ac.uk/sgp/large/sgp.htm https://bruceravel.github.io/demeter/artug/atoms/space.html https://www.ruppweb.org/Xray/comp/space_instr.htm

nte@rated syst©ns Multi-functions Self-healing 2D carbon Solar cells batte 2D MXenes 2D organic frameworks MESDs rosupercapacitors 链 Electrochromic 2D chalcogenides 8/06U06880 2D oxides e/qeyojMsoweuL e64 elqeysiens 2D hydroxides SJojeJeue Lrowew-edeys S/ojejepoyoud
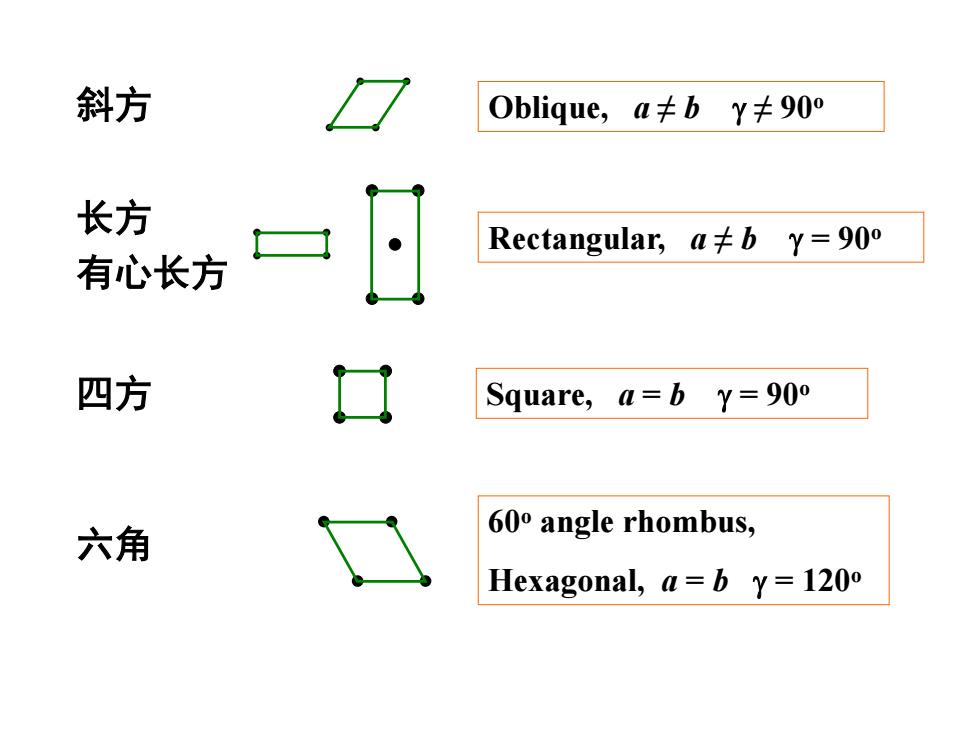
斜方 Oblique,a≠by≠90° 长方 Rectangular,a4b y=900 有心长方 四方 口 Square,a=bY=90° 六角 600 angle rhombus, Hexagonal,a=b y=1200
Oblique, a ≠ b ≠ 90o Rectangular, a ≠ b = 90o Square, a = b = 90o 60o angle rhombus, Hexagonal, a = b = 120o 斜方 长方 有心长方 四方 六角

点对称条件 晶系 京群 布拉菲点阵 1(E)或1(0 三斜 1(y1(c) P 2(c2)或2(m) 单斜2(Cym(c2Im(c2d P,B 两个2(c2)或2m)正交222(D2,mm2(C2v):mmm(D2) P,C,F 4(C4或4(S43) 四方4(Cdy/m(Cn,4mm(Cy/mmm(Dh, P, 422D,4(S,④2m(D2 3(C3)或3(S65) 三方 3(Ca3m (Cavl 32(D3), P 3(S:),3m(D3d) 6(C6)或6(S35) 六方6(Cm(C66mm(C6d√mmm(Da,P 622(D),6(C3),62(D3d 四个三次轴 立方23,m3巴b3mTa P,1,下 432(0),m3m(0h)
点对称条件 晶系 点群 四个三次轴 三 斜 单 斜 正 交 四 方 三 方 六 方 立 方 1(E)或1(i) 2(C2 )或2(m) 两个2(C2 )或2(m) 4(C4 )或4(S4 3 ) 3(C3 )或3(S6 5 ) 6(C6 )或6(S3 5 ) 布拉菲点阵 P P, B P, C, I, F P, I P P, I, F P 1(C1 ), 1(Ci ) m(C1h 2(C ), 2 ), 2/m(C2h) 222(D2 ), mm2(C2v), mmm(D2h) 42m (D2d 4 (S ) 4 422 (D ), 4 ), 4/mmm(D4h 4mm(C ), 4v 4/m(C ), 4h 4(C ), 4 ), 3m(D3d) 3(C3 ), 3m (C3v), 32(D3 ), 3(S6 ), 622 (D6 ), 6/mmm (D6h 6mm(C ), 6v 6/m(C ), 6h 6(C ), 6 ), 62 (D3h 6 (C ) 3h), 23(T), m3 (Th ), 432 (O), m3m (Oh ) 43m (Td ),

晶系 点群 布拉菲京阵 73种点式空间群 三 斜1,i P P1, P1 单斜2,m,2/m P P2,Pm,P2/m B B2,Bm, B2/m 正交 222, mm2, mmm P222, Pmm2, Pmmm C222, Cmm2, Cmmm, Amm2 I222, Imm2, Immm F F222, Fmm2, Fmmm 四方 4,4/m,4mm,422. p P4,P4/m,P4mm,P4/mmm,P422,P4,P42m,P4m2 不, 42m,4/mmm I4,14/m,14mm,I4/mmm,1422,4,42m,4m2 三方 3,3m,32, P P3,P3ml,P312,P3,P31m,P31m,P321,P3ml ! 3,3m R R3,R3m,R32,R3,R3m 六方 6,6/m,6mm,622 P6,P6/m,P6mm,P6/mmm,P622,P6,P6m2,P62m 6, 62m,6/mmm 立方 23,m3,43m, P23,Pm3,P43m,P432,Pm3m 432,m3m I23,Im3,43m,I432,Im3m F23,Fm3,F43m,F432,Fm3m
晶系 点群 布拉菲点阵 73种点式空间群 三 斜 单 斜 正 交 四 方 三 方 六 方 立 方 P P P P P P P 1, 1 2, m, 2/m 222, mm2, mmm 4, 42m, 422, 4/mmm 4, 4/m, 4mm, 3m 3, 3m, 32, 3, 622, 6/mmm 6, 6/m, 6mm, 6, 62m, 23, m3, 432, m3m 43m, P1, P1 P2, Pm, P2/m P222, Pmm2, Pmmm P4, P4/m, P4mm, P4/mmm,P422, P4, P42m, P3, P3m1, P312, P3, P31m, P23, Pm3, P43m, P432, Pm3m B2, Bm, B2/m C222, Cmm2, Cmmm, I222, Imm2, Immm F222, Fmm2, Fmmm Amm2 B C I F I P4m2 I4, I4/m, I4mm, I4/mmm, I422, I4, I42m, I4m2 R R3, R3m, R32, R3, R3m P31m, P321, P3m1 P6, P6/m, P6mm, P6/mmm,P622, P6, P6m2, P62m I F I23, Im3, I43m, I432, Im3m F23, Fm3, F43m, F432, Fm3m

十七种二维空间群 点阵 点群 空间群 序号 对应图像 斜形 1 P1 1 p 2 p211 2 p1m1 3 e e m p1g1 4 矩形 c1m1 5 6 P,c p2mm 特 ◆ 特 2mm p2mg 7 特 p2gg(h *格 ◆ 然 c2mm 9 正方形 4 p4 10 4mm p4mm 11 p p4gm (g) 12 3 p3 13 WW 六方形 3m p3m1 14 Www p31m 15 W p 6 p6 16 火 6mm p6mm 17
十七种二维空间群 点阵 点群 空间群 序号 斜形 1 p1 1 对应图像 p 矩形 p, c 正方形 p 六方形 p 2 p211 4 p4 3 3m 6 6mm p3 p3m1 p31m p6 p6mm 2 p2mm p2mg p2gg (n) c2mm 2mm 6 7 8 9 10 p4mm p4gm (g) 4mm 11 12 13 14 15 16 17 p1m1 p1g1 c1m1 m 3 4 5
The 17 Two-dimensional Space Groups Equivalent positions,Symmetry,and Possible reflections p2 p211 O Origin on 1 Origin at 2 2 e 1 七,乃文, Number of positions, Wyckoff notation, 1 d 2 1/2,1/2. and point symmetry 1 c 2 1/2,0. 1 b 2 0,1/2. 1 a 1 x 1 a 2 0,0
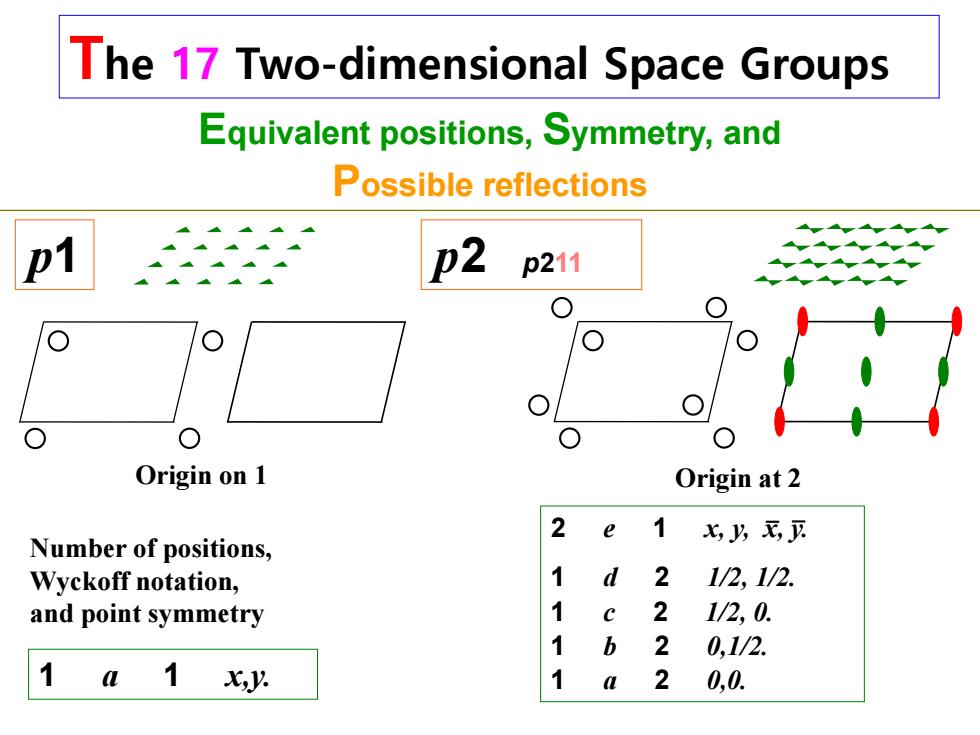
The 17 Two-dimensional Space Groups Equivalent positions, Symmetry, and Possible reflections p1 p2 p211 1 a 1 x,y. Origin on 1 Number of positions, Wyckoff notation, and point symmetry Origin at 2 2 e 1 x, y, x, y. 1 d 2 1/2, 1/2. 1 c 2 1/2, 0. 1 b 2 0,1/2. 1 a 2 0,0

pm p1m1 会会今 cm c1m1 ÷ 合 ① ① ① ① O O ① O 0 0 0 0 0 Origin on m Origin on m Co-ordinates of equivalent positions 2 1 七,水 (0,0;1/2,1/2)+ 1 b m 1/2, 1 0,y 4 b 1 m 七,;, 2 a m 0, ① pg pig1 0 Origin on g 2 1 X,; x,1/2+
pm p1m1 pg p1g1 cm c1m1 , , , , Origin on m 2 c 1 x, y; x,y. 1 b m 1/2, y. 1 a m 0, y. Origin on m 4 b 1 x, y; x, y. 2 a m 0, y. , , , , , Co-ordinates of equivalent positions (0,0; 1/2,1/2)+ , , Origin on g 2 a 1 x, y; x,1/2+y
给转的的 pmm p2mm 特 % 特 特 pmg p2mg O① 0 ① ①O O▣ O ① ①O ① ① Origin at 2mm 4 i 1 防y防反 Origin at 2 4 d 1 xy防h+比万-比水 2 h m ;,反 2 8 m 0,50, 2 m 防巫 2 f m 七,12;1/2. 2 七,050. 2 b 2 0,6;h五. e m 2 a 2 0,05 2,0. 1 d mm 1/2,1/2. 1 mm 1/2,0. 1 b mm 0,1/2. 1 a mm 0,0
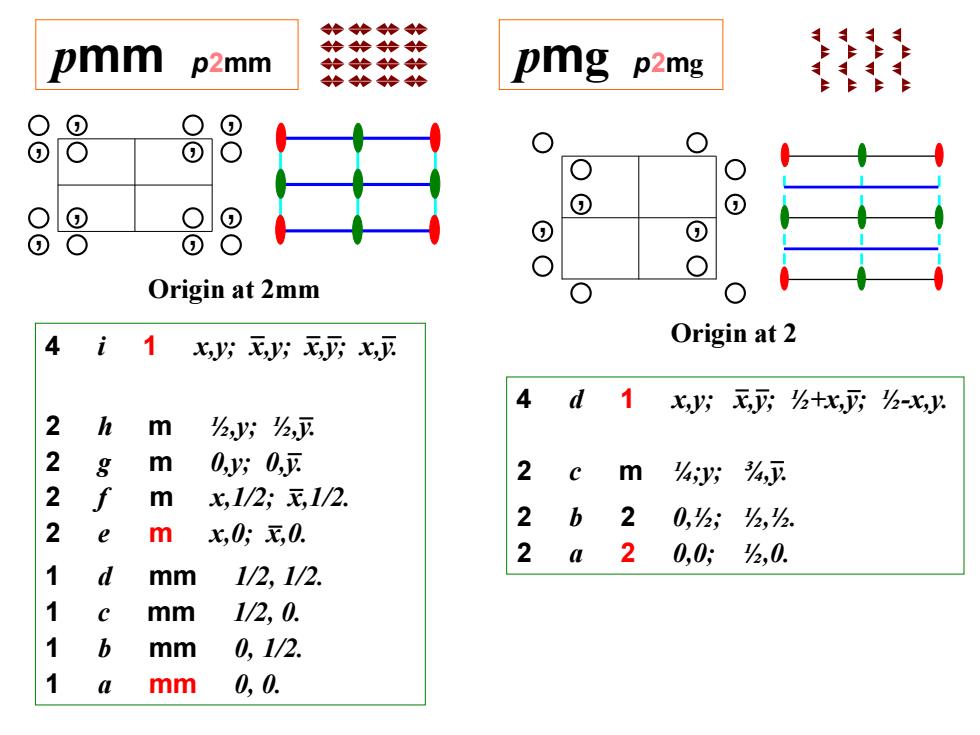
pmm p2mm pmg p2mg Origin at 2mm Origin at 2 4 i 1 x,y; x,y; x,y; x,y. 2 h m ½,y; ½,y. 2 g m 0,y; 0,y. 2 f m x,1/2; x,1/2. 2 e m x,0; x,0. 1 d mm 1/2, 1/2. 1 c mm 1/2, 0. 1 b mm 0, 1/2. 1 a mm 0, 0. , , , , , , , , , , , , 4 d 1 x,y; x,y; ½+x,y; ½-x,y. 2 c m ¼;y; ¾,y. 2 b 2 0,½; ½,½. 2 a 2 0,0; ½,0