
4.2费涅耳圆孔衍射和圆屏衍射 实验现象 半波带法(简单介绍) 菲涅耳波带片(简单介绍)
4.2 费涅耳圆孔衍射和圆屏衍射 实验现象 半波带法(简单介绍) 菲涅耳波带片(简单介绍)

一、实验现象 一般参数: 圆孔半径:p~1mm 源屏距离:R~lm 屏屏距离:b~3-5m P。 R b
一、 实验现象 一般参数: 圆孔半径:𝜌~1mm 源屏距离:R~1m 屏屏距离:b~3-5m
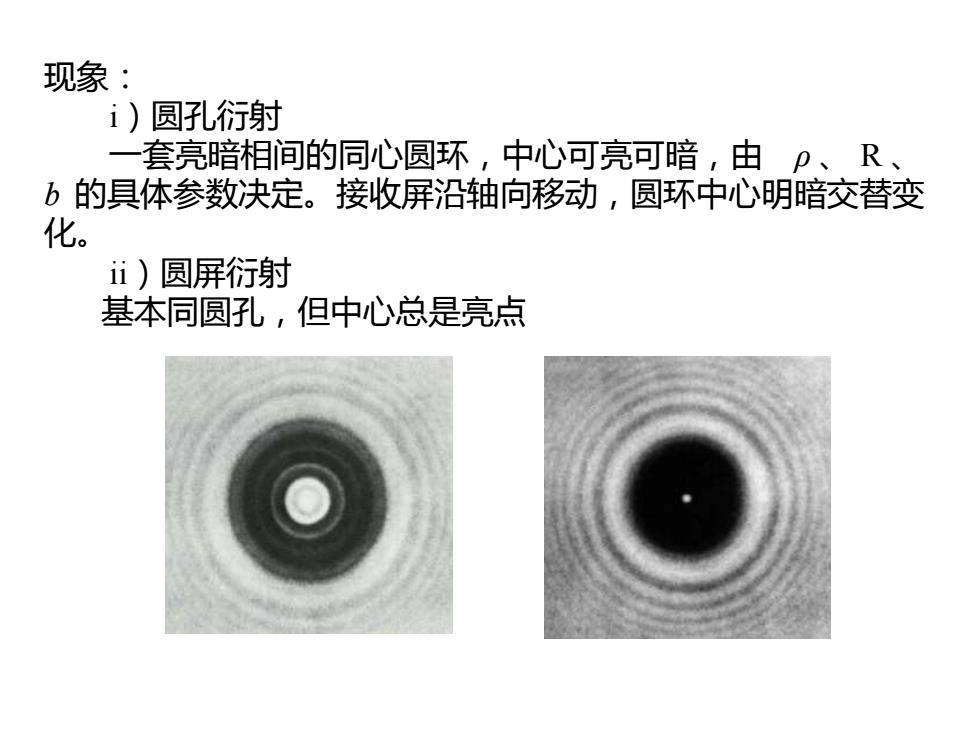
现象: i)圆孔衍射 一套亮暗相间的同心圆环,中心可亮可暗,由p、R、 b的具体参数决定。接收屏沿轴向移动,圆环中心明暗交替变 化。 ⅱ)圆屏衍射 基本同圆孔,但中心总是亮点
现象: i)圆孔衍射 一套亮暗相间的同心圆环,中心可亮可暗,由 ρ 、 R 、 b 的具体参数决定。接收屏沿轴向移动,圆环中心明暗交替变 化。 ii)圆屏衍射 基本同圆孔,但中心总是亮点
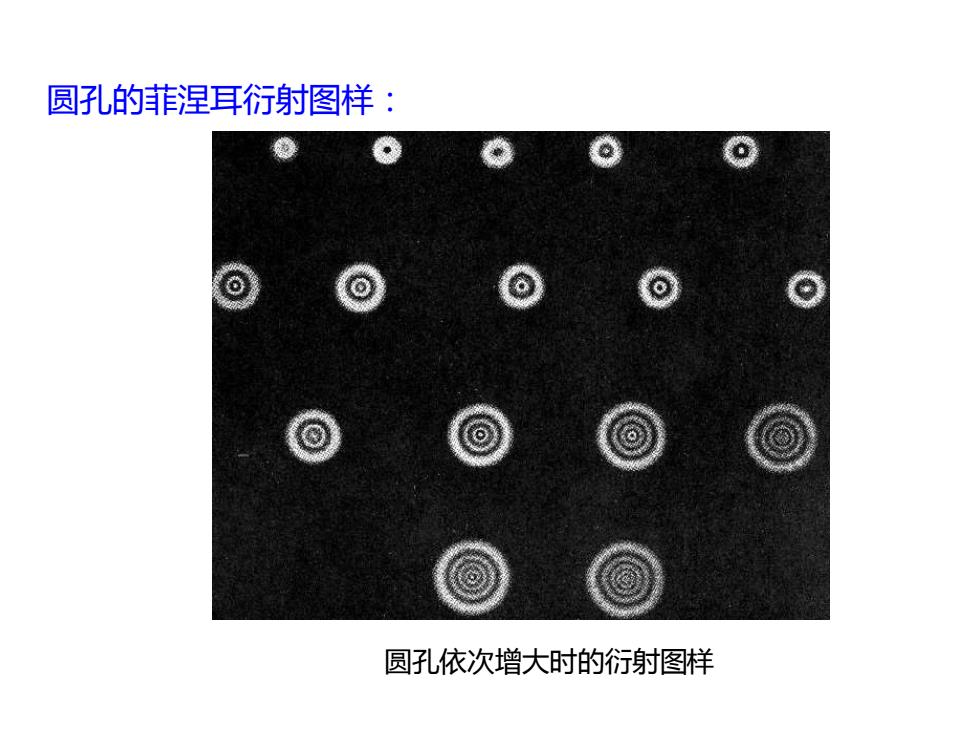
圆孔的菲涅耳衍射图样: 圆孔依次增大时的衍射图样
圆孔的菲涅耳衍射图样: 圆孔依次增大时的衍射图样
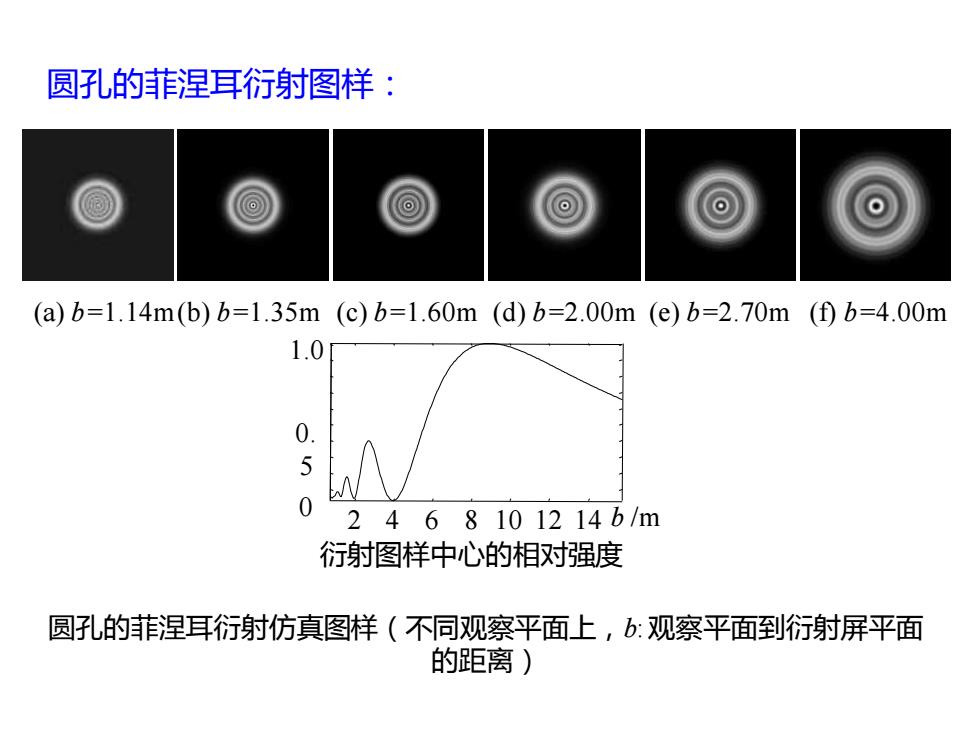
圆孔的菲涅耳衍射图样: ⊙ (a)b=1.14m(b)b=1.35m(c)b=1.60m(d))b=2.00m(e)b=2.70m(fb=4.00m 1.0 05 2468101214b/m 衍射图样中心的相对强度 圆孔的菲涅耳衍射仿真图样(不同观察平面上,b:观察平面到衍射屏平面 的距离)
圆孔的菲涅耳衍射图样: 圆孔的菲涅耳衍射仿真图样(不同观察平面上,b: 观察平面到衍射屏平面 的距离) (a) b=1.14m(b) b=1.35m (c) b=1.60m (d) b=2.00m (e) b=2.70m (f) b=4.00m 衍射图样中心的相对强度 2 4 6 8 10 12 14 b /m 1.0 0. 5 0
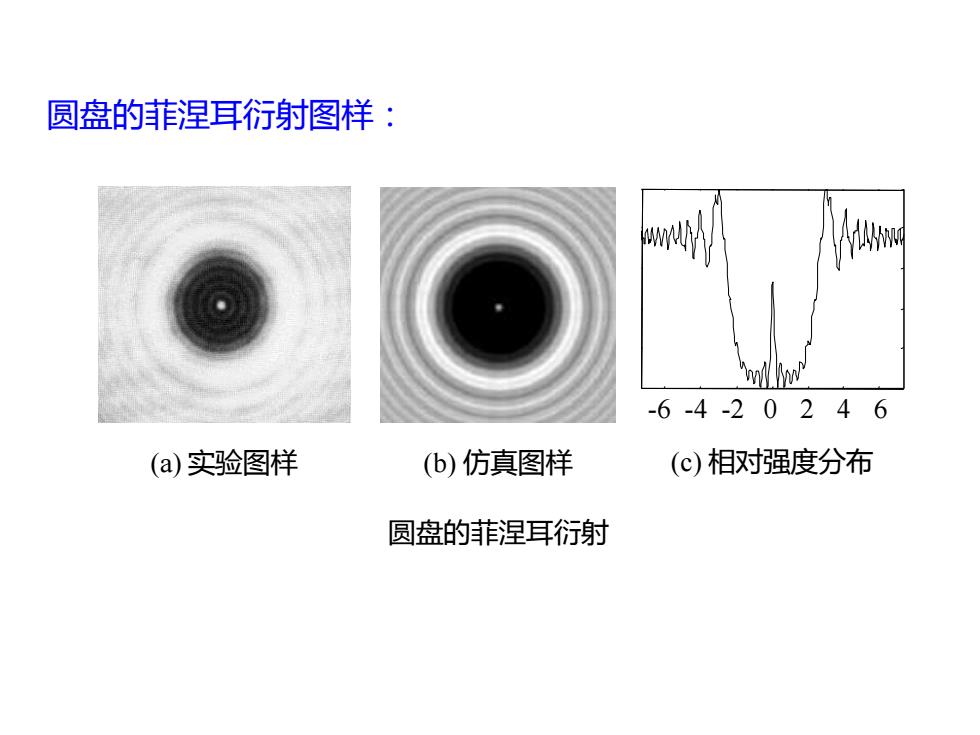
圆盘的菲涅耳衍射图样: W -6-4-20246 (a)实验图样 (b)仿真图样 (c)相对强度分布 圆盘的菲涅耳衍射
圆盘的菲涅耳衍射图样: 圆盘的菲涅耳衍射 (b) 仿真图样 (c) 相对强度分布 -6 -4 -2 0 2 4 6 (a) 实验图样
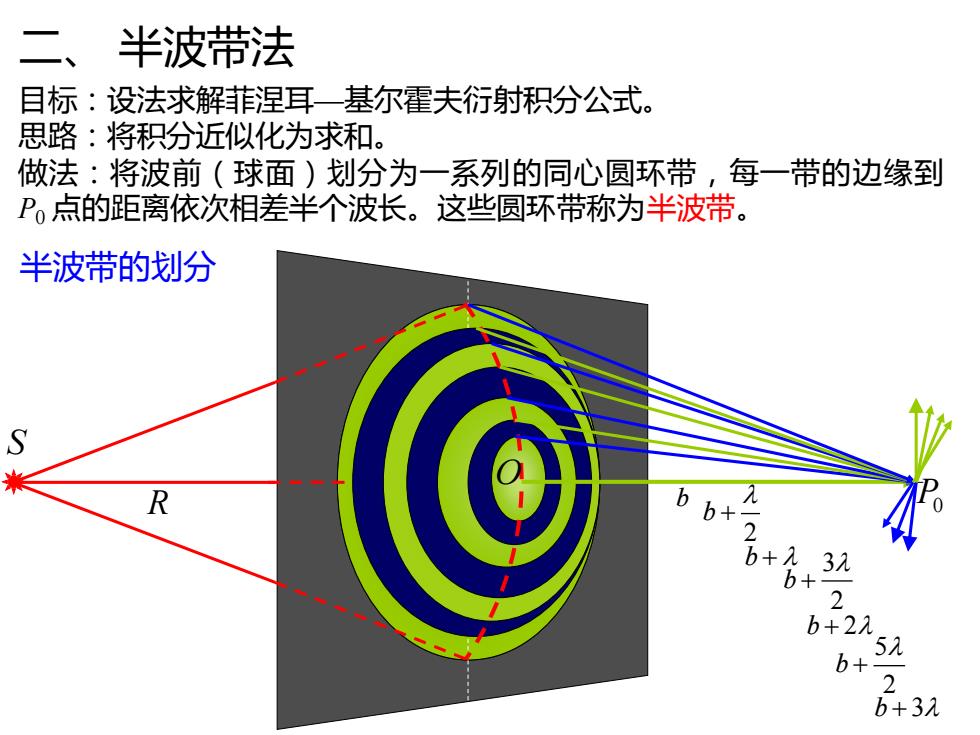
二、半波带法 目标:设法求解菲涅耳一基尔霍夫衍射积分公式。 思路:将积分近似化为求和。 做法:将波前(球面)划分为一系列的同心圆环带,每一带的边缘到 P。点的距离依次相差半个波长。这些圆环带称为半波带。 半波带的划分 S R bb* ++ 2 b+2元 B:SA 2 b+3入
二、 半波带法 目标:设法求解菲涅耳—基尔霍夫衍射积分公式。 思路:将积分近似化为求和。 做法:将波前(球面)划分为一系列的同心圆环带,每一带的边缘到 P0 点的距离依次相差半个波长。这些圆环带称为半波带。 b 2 b + 3 2 b + b + b + 2 5 2 b + b + 3 R P0 S O 半波带的划分
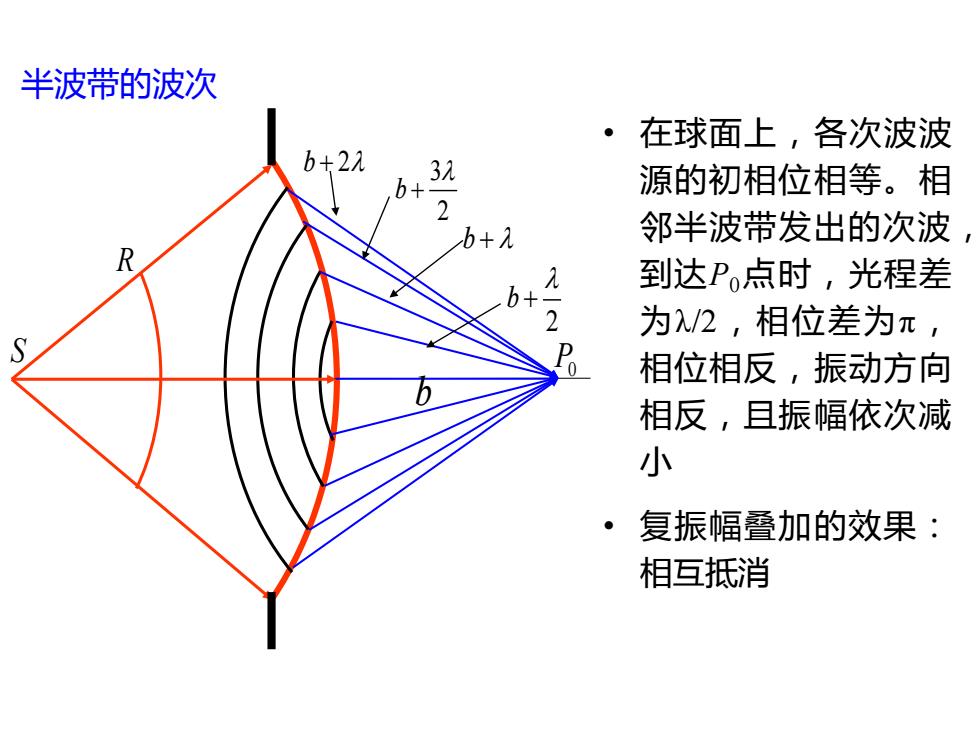
半波带的波次 ·在球面上,各次波波 b+22 3 5+ 源的初相位相等。相 邻半波带发出的次波 R 入 到达P点时,光程差 b 2 为/2,相位差为元, S 0 相位相反,振动方向 相反,且振幅依次减 小 。 复振幅叠加的效果: 相互抵消
R b 2 b + b + 32 b + b + 2 半波带的波次 • 在球面上 ,各次波波 源的初相位相等 。 相 邻半波带发出的次波 , 到达 P 0点时 ,光程差 为λ/ 2 ,相位差为 π , 相位相反 ,振动方向 相反 ,且振幅依次减 小 • 复振幅叠加的效果: 相互抵消 S P0
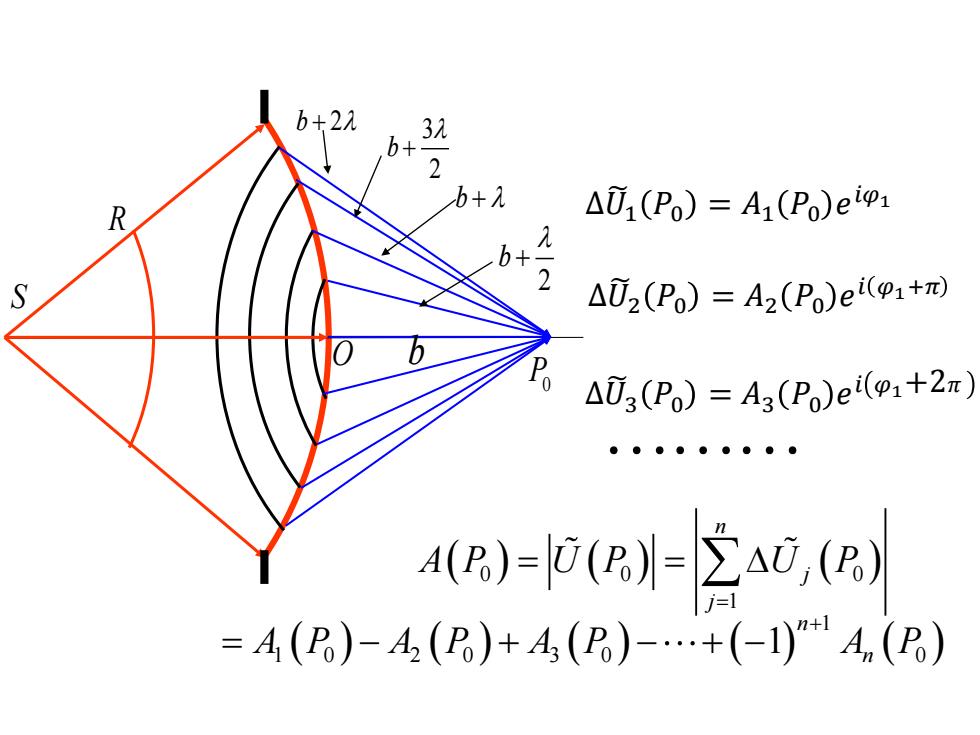
b+2A 3 b*2 b+入 R △01(Po)=A1(Po)eio1 b+ S AU2(Po)=Az(Po)ei(+n AU3(Po)=A3(Po)ei(1+2r) ●●●●●●●● 4(e)-(C2A,(B =4(P)-A,()+4(B)-+(-1)A(R)
R b 2 b + b + 3 2 b + b + 2 S O Δ𝑈෩1 𝑃0 = 𝐴1 𝑃0 𝑒 𝑖𝜑1 Δ𝑈෩2 𝑃0 = 𝐴2 𝑃0 𝑒 𝑖 𝜑1+𝜋 Δ𝑈෩3 𝑃0 = 𝐴3 𝑃0 𝑒 𝑖 𝜑1+2𝜋 ( 0 0 0 ) ( ) ( ) 1 n j j A P U P U P = = = ( ) ( ) ( ) ( ) ( ) 1 1 0 2 0 3 0 0 1 n A P A P A P A P n + = − + − + − P0
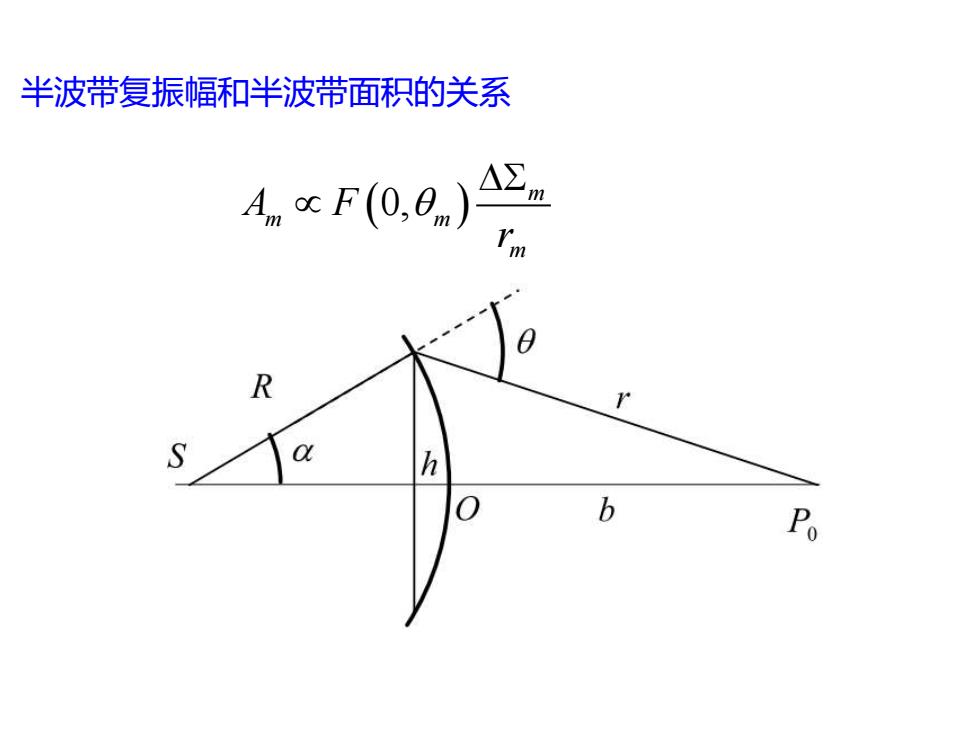
半波带复振幅和半波带面积的关系 A。cF0,8)Aa R S h b %
(0, ) m m m m A F r 半波带复振幅和半波带面积的关系