
Chapter 1 The Schrodinger Equation 1.1 (a)F:(b)T:(c)T. 1.2 (a)Ephoton=hm=hcl元=(6.626×104Js2.998×108m/s)/1064×109m) 1.867×1019J (b)E=(5×10Js2×108s)=0.1J=m1.867×1019)andn=5×1017 1.3 Use of Ephoton hc/a gives E-602x102X6626×104Js298×10m9-399J 300×109m 1.4(a))Tma=hw-Φ= (6.626×104Js2.998×108ms)200×10m)-(2.75eV1.602×1019J/eV)= 5.53×1019J=3.45eV and1=4.51×10m=451m. (c)Since the impure metal has a smaller work function,there will be more energy left over after the electron escapes and the maximum T is larger for impure Na. 1.5 (a)At high frequencies,we have e>>1and the-1 in the denominator of Planck's formula can be neglected to give Wien's formula. (b)The Taylor series for the exponential function is ex=+x+x/1+.Forx< we can neglect x and higher powers to give.Takingxh/,we have for Planck's formula at low frequencies ✉-m 2πhm3 1.61=h/mw=137h/mc=137(6.626×104Js)9.109×1031kg)2.998×103m/s)= 3.32×100m=0.332nm. 1.1 Copyright2014 Pearson Education.Ine
1-1 Copyright © 2014 Pearson Education, Inc. Chapter 1 The Schrödinger Equation 1.1 (a) F; (b) T; (c) T. 1.2 (a) photon E h hc == = ν /λ (6.626 × 10–34 J s)(2.998 × 108 m/s)/(1064 × 10–9 m) = 1.867 × 10–19 J. (b) E = (5 × 106 J/s)(2 × 10–8 s) = 0.1 J = n(1.867 × 10–19 J) and n = 5 × 1017. 1.3 Use of photon E hc = /λ gives 23 34 8 9 (6.022 10 )(6.626 10 J s)(2.998 10 m/s) 399 kJ 300 10 m E − − ×× × = = × 1.4 (a) T h max = −Φ= ν (6.626 × 10–34 J s)(2.998 × 108 m/s)/(200 × 10–9 m) – (2.75 eV)(1.602 × 10–19 J/eV) = 5.53 × 10–19 J = 3.45 eV. (b) The minimum photon energy needed to produce the photoelectric effect is (2.75 eV)(1.602 × 10–19 J/eV) = hν =hc/λ = (6.626 × 10–34 J s)(2.998 × 108 m/s)/λ and λ = 4.51 × 10–7 m = 451 nm. (c) Since the impure metal has a smaller work function, there will be more energy left over after the electron escapes and the maximum T is larger for impure Na. 1.5 (a) At high frequencies, we have / 1 b T e ν >> and the −1 in the denominator of Planck’s formula can be neglected to give Wien’s formula. (b) The Taylor series for the exponential function is 2 1 /2! . x e xx =+ + +" For x << 1, we can neglect 2 x and higher powers to give 1 . x e x − ≈ Taking x ≡ h kT ν / , we have for Planck’s formula at low frequencies 3 3 32 / 2/ 2 2 2 22 1 ( 1) ( / ) b T h kT a h h kT e c e c h kT c ν ν ν π ν π ν πν ν = ≈= − − 1.6 λ = h m/ v = = 137 / h mc 137(6.626 × 10–34 J s)/(9.109 × 10–31 kg)(2.998 × 108 m/s) = 3.32 × 10–10 m = 0.332 nm

1.7 Integration gives x=g+(go+vo)+c2.If we know that the particle had position xo at time to:then xo=-gto+(glo+Vo)to+c2 and c2=xo-gto-Volo.Substitution of the expression for c2 into the equation for x givesx=g()2+vo(r-t). 1.8 -h/0ag1a)=-22mXa2Ψar2)+y.ForΨ=ae,we find aΨ/al=-ibΨ,aΨ/ax=-2bmhxΨ,anda2Ψ/ax2=-2bmh-lΨ-2bmh-x(a平/ax) =-2 bmhΨ-2bmh'x(-2bmh'xΨ)=-2bmhlΨ+4b2m2h2x2Ψ.Substituting into the time-dependent Schrodinger equation and then dividing by we get -(h/i)(-ib)=-(h2/2m)(-2bmh+4b2m2h2x2)+and V=2b2mx? 1.9 (a)F;(b)F.(These statements are valid only for stationary states.) 1.10 satisfies the time-independent Schrodinger (1.19)./x=be2bcxe; wx=-2bcxe-4bcxe+b=-6bcxe+4bxe Equation (1.19)becomes (-h2/2mX-6bcxe+4bc2xe)+(2c2h2x2/m)bxe-=Ebxe Thex'terms cancel and E=3h2c/m= 36.626×10-34Js)22.00(109m)214π2(1.00×10-30kg)=6.67×10-20J 1.11 Only the time-dependent equation. 1.12(a)|ΨPdk=(2/b3)x2e24bdk= 2(3.0×109m)3(0.90×109m)2e20.90m3.0nm(0.0001×109m)=3.29×106 (b)For x20,we havex=x and the probability is given by (1.23)and (A.7)as r本=2/6)jre2bx=2/be2(-bx2n-b22-61④呢m= -e2(x21b2+xb+1/26m=-e8(4/9+23+/2)+/2=0.0753. (c)is zero atx=0,and this is the minimum possible probability density. (@∫IΨPk=(2Ib)f°x2e2wb+(2b)小0re2 ds.Let w=-in the first integral on the right This integral becomes which equals the second integral on the right [see Eq.(4.10)].Hence ∫IΨ&=(4/b)j0xe2bk=(4/b'2/(b/2月=1,where(A8)in the Appendix was used. 1-2 Copyright2014 Pearson Education.Inc
1-2 Copyright © 2014 Pearson Education, Inc. 1.7 Integration gives 1 2 2 00 2 x =− + + + gt gt t c ( ). v If we know that the particle had position 0x at time 0t , then 1 2 0 0 0 00 2 2 x =− + + + gt gt t c ( ) v and 1 2 2 0 0 00 2 c x gt t =− − v . Substitution of the expression for 2c into the equation for x gives 1 2 0 0 00 2 x =− − + − x gt t t t ( ) ( ). v 1.8 2 22 − ∂Ψ ∂ =− ∂ Ψ ∂ + Ψ ( / )( / ) ( /2 )( / ) = = i t m xV . For 2 / , ibt bmx ae e − − Ψ = = we find ∂Ψ ∂ = − Ψ / t ib , 1 /2 , x bm x − ∂Ψ ∂ = − Ψ = and 22 1 1 / 2 2 ( /) x bm bm x x − − ∂ Ψ ∂ = − Ψ − ∂Ψ ∂ = = = 1 1 1 1 2 2 22 2 2 (2 ) 2 4 bm bm x bm x bm b m x − −− − − − Ψ− − Ψ =− Ψ+ Ψ = == = = . Substituting into the time-dependent Schrödinger equation and then dividing by Ψ, we get 2 1 2 2 22 ( / )( ) ( /2 )( 2 4 ) i ib m bm b m x V − − − − Ψ =− − + Ψ+ Ψ = = == and 2 2 V b mx = 2 . 1.9 (a) F; (b) F. (These statements are valid only for stationary states.) 1.10 ψ satisfies the time-independent Schrödinger (1.19). 2 / cx ψ x be− ∂ ∂= 2 2 2 cx bcx e− − ; 2 2 2 / 2 cx ψ x bcxe− ∂ ∂ =− − 2 2 2 3 4 4 cx cx bcxe bc x e − − + = 2 2 2 3 6 4 cx cx bcxe bc x e − − − + . Equation (1.19) becomes 2 2 2 23 ( /2 )( 6 4 ) cx cx m bcxe bc x e − − −− + = + 2 2 222 (2 / ) cx cx c x m bxe Ebxe − − = = . The x 3 terms cancel and 2 E cm = = 3 / = 3(6.626 × 10–34 J s)2 2.00(10–9 m)–2/4π 2 (1.00 × 10–30 kg) = 6.67 × 10–20 J. 1.11 Only the time-dependent equation. 1.12 (a) 2 3 2 2| |/ | | (2/ ) x b dx b x e dx − Ψ= = 9 3 9 2 2(0.90 nm)/(3.0 nm) 9 2(3.0 10 m) (0.90 10 m) (0.0001 10 m) e −− − − − ×× × = 3.29 × 10–6. (b) For 0, x ≥ we have | | x = x and the probability is given by (1.23) and (A.7) as 2 nm 2 nm 2 3 2 2 / 3 2 / 2 2 3 2 nm 0 0 0 | | (2 / ) (2 / ) ( /2 /2 /4) | x b xb dx b x e dx b e bx xb b − − Ψ= = − − − ∫ ∫ = 2 / 2 2 2 nm 0 ( / / 1/2) | x b e x b xb − − ++ = 4/3 e (4/9 2/3 1/2) 1/2 − − ++ + = 0.0753. (c) Ψ is zero at x =0, and this is the minimum possible probability density. (d) 0 2 3 22/ 3 2 2/ 0 | | (2/ ) (2/ ) . xb xb dx b x e dx b x e dx ∞ ∞ − −∞ −∞ Ψ= + ∫∫ ∫ Let w = –x in the first integral on the right. This integral becomes 0 2 2/ 2 2/ 0 () , wb wb w e dw w e dw ∞ − − ∞ − = ∫ ∫ which equals the second integral on the right [see Eq. (4.10)]. Hence 2 3 2 2/ 3 3 0 | | (4 / ) (4 / )[2!/ ( / 2) ] x b dx b x e dx b b ∞ ∞ − −∞ Ψ= = ∫ ∫ = 1, where (A.8) in the Appendix was used

1.13 The interval is small enough to be considered infinitesimal(since changes negligibly whthis interval.)At1=0,we have1YP在=g2/元cyr2e-2rie在- [32/x2.00A)1(2.00A)2e2(0.001A)=0.000216. 4r=mae2aok=eaa2=(em+em2= 1.5001nm 4.978×106 1.15 (a)This function is not real and cannot be a probability density. (b)This function is negative whenxand cannot be a probability density. (c)This function is not normalized(unless b=)and can't be a probability density. 1.16 (a)There are four equally probable cases for two children:BB,BG,GB,GG,where the first letter gives the gender of the older child.The BB possibility is eliminated by the given information.Of the remaining three possibilities BG.GB.GG.only one has two girls,so the probability that they have two girls is 1/3. (b)The fact that the older child is a girl eliminates the BB and BG cases,leaving GB and GG.so the probability is 1/2 that the younger child is a girl. 1.17 The 138 peak arises from the case CCF,whose probability is(0.9889)2=0.9779 The 139 peak arises from the cases CCFsandCCF whose probability is (0.9889x0.011)+(0.011IX0.9889=0.02195.The140 peak arises from5ccF6 whose probability is(0.0111)2=0.000123.(As a check,these add to 1.)The 139 peak height is(0.02195/0.9779)100=2.24.The140 peak height is(0.000123/0.9779)100= 0.0126. 1.18 There are 26 cards,2 spades and 24 nonspades,to be distributed between B and D. Imagine that 13 cards,picked at random from the 26,are dealt to B.The probability that every card dealt to B is a nonspade is装器号}告是是==÷.Likewise,the probability that Dgets 13 nonspades isIf B does not get all nonspades and D does not get all nonspades,then each must get one of the two spades and the probability that each gets one spade is 1-=13/25.(A commonly given answer is:There are four possible outcomes,namely,both spades to B,both spades to D,spade I to B and spade 2 to D.spade 2 to B and spade 1 to D.so the probability that each gets one spade is 2/4= 1/2.This answer is wrong,because the four outcomes are not all equally likely.) 1-3 Copyright2014 Pearson Education.Inc
1-3 Copyright © 2014 Pearson Education, Inc. 1.13 The interval is small enough to be considered infinitesimal (since Ψ changes negligibly within this interval). At t = 0, we have 2 2 2 6 1/2 2 2 / | | (32 / ) x c dx c x e dx π − Ψ = = [32/π(2.00 Å)6 ] 1/2(2.00 Å)2 e –2 (0.001 Å) = 0.000216. 1.14 2 1 2/ 2/ 1.5001 nm 1.5001 nm 1.5000 nm 1.5000 nm | | /2| b xa xa a dx a e dx e −− − Ψ = =− = ∫ ∫ (–e –3.0002 + e –3.0000)/2 = 4.978 × 10–6. 1.15 (a) This function is not real and cannot be a probability density. (b) This function is negative when x < 0 and cannot be a probability density. (c) This function is not normalized (unless ) b = π and can’t be a probability density. 1.16 (a) There are four equally probable cases for two children: BB, BG, GB, GG, where the first letter gives the gender of the older child. The BB possibility is eliminated by the given information. Of the remaining three possibilities BG, GB, GG, only one has two girls, so the probability that they have two girls is 1/3. (b) The fact that the older child is a girl eliminates the BB and BG cases, leaving GB and GG, so the probability is 1/2 that the younger child is a girl. 1.17 The 138 peak arises from the case 12C12CF6, whose probability is (0.9889)2 = 0.9779. The 139 peak arises from the cases 12C13CF6 and 13C12CF6, whose probability is (0.9889)(0.0111) + (0.0111)(0.9889) = 0.02195. The 140 peak arises from 13C13CF6, whose probability is (0.0111)2 = 0.000123. (As a check, these add to 1.) The 139 peak height is (0.02195/0.9779)100 = 2.24. The 140 peak height is (0.000123/0.9779)100 = 0.0126. 1.18 There are 26 cards, 2 spades and 24 nonspades, to be distributed between B and D. Imagine that 13 cards, picked at random from the 26, are dealt to B. The probability that every card dealt to B is a nonspade is 24 22 21 14 12 23 13 6 13(12) 26 25 24 23 16 15 14 26(25) 25 " = = . Likewise, the probability that D gets 13 nonspades is 6 25 . If B does not get all nonspades and D does not get all nonspades, then each must get one of the two spades and the probability that each gets one spade is 6 6 25 25 1 13 /25 −−= . (A commonly given answer is: There are four possible outcomes, namely, both spades to B, both spades to D, spade 1 to B and spade 2 to D, spade 2 to B and spade 1 to D, so the probability that each gets one spade is 2/4 = 1/2. This answer is wrong, because the four outcomes are not all equally likely.)

1.19 (a)The Maxwell distribution of molecular speeds:(b)the normal (or Gaussian) distribution. 1.20 (a)Real;(b)imaginary;(c)real;(d)imaginary;(e)imaginary:(f)real; (g)real;(h)real;(1)real. 1.21 (a)A point on thex axis three units to the right of the origin. (b)A point on theyaxis one unit below the origin. (c)A point in the second quadrant withx coordinate-2 andy coordinate +3. 1.23(a)2=-1.(b)=i2=i(-1)=-i.(c)=(2)2=(-1)2=1. (d)i=(-)i=1 (e)(1+5i)2-30)=2+101-31-152=17+7i. 0-6201-0 1.24(a4(b)2,(d6-3元,(d2e5 1.25(a)1,90°:(b)2,π/3 (e)-2e=2(-)e3.Since-1 has absolute value I and phase we have =2e=2e()=re,so the absolute value is2 and the phase is 4/3 radians (d1zl=(x2+y2)2=2+(-2}2]2=52;tan6=y/x=-2/1=-2and 0=-63.4°=296.6°=5.176 radians. 1.26 On a circle of radius 5.On a line starting from the origin and making an angle of 45 with the positivex axis. 1.27(a)i=ler12,(b)-1=le; (c)Using the answers to Prob.1.25(d),we have 5276 (dr=[(-1)2+(-1)2]2=22;0=180°+45°=225°=3.927rad,22e3.927 1.28 (a)Using Eq.(1.36)with n=3,we have e=1, e2m/)=cos(2π/3)+isin(2r/3)=-0.5+i5/2,ande4m/3)-0.5-i5/2. 1-4 Education.Inc
1-4 Copyright © 2014 Pearson Education, Inc. 1.19 (a) The Maxwell distribution of molecular speeds; (b) the normal (or Gaussian) distribution. 1.20 (a) Real; (b) imaginary; (c) real; (d) imaginary; (e) imaginary; (f) real; (g) real; (h) real; (i) real. 1.21 (a) A point on the x axis three units to the right of the origin. (b) A point on the y axis one unit below the origin. (c) A point in the second quadrant with x coordinate –2 and y coordinate +3. 1.22 2 1 1 1 ii i i i ii i = = = =− − 1.23 (a) 2 i = −1. (b) 3 2 i ii i i = = − =− ( 1) . (c) 4 22 2 i i = ( ) ( 1) 1. =− = (d) * ( ) 1. ii ii =− = (e) 2 (1 5 )(2 3 ) 2 10 3 15 17 7 . + − =+ − − = + i i ii i i (f) 1 3 1 3 4 2 4 14 6 2 14 0.1 0.7 . 4 2 4 2 4 2 16 8 8 4 20 i ii i i i i i i ii − − − − − −− = = = =− − + + − +−+ 1.24 (a) –4 (b) 2i; (c) 6 – 3i; (d) /5 2 . i e π 1.25 (a) 1, 90°; (b) 2, π/3; (c) /3 /3 2 2( 1) . i i ze e π π =− = − Since –1 has absolute value 1 and phase π, we have /3 (4 /3) 22 , ii i i z e e e re π π πθ = == so the absolute value is 2 and the phase is 4π/3 radians. (d) 2 2 1/2 2 2 1/2 1/2 | | ( ) [1 ( 2) ] 5 ; z xy = + = +− = tan / 2 / 1 2 θ = y x =− =− and θ = –63.4° = 296.6° = 5.176 radians. 1.26 On a circle of radius 5. On a line starting from the origin and making an angle of 45° with the positive x axis. 1.27 (a) /2 1 ; i i e π = (b) 11 ; i e π − = (c) Using the answers to Prob. 1.25(d), we have 1/2 5.176 5 ;i e (d) 2 2 1/2 1/2 r = − + − = = °+ °= °= [( 1) ( 1) ] 2 ; 180 45 225 3.927 θ rad; 1/2 3.927 2 .i e 1.28 (a) Using Eq. (1.36) with n = 3, we have 0 1, i e ⋅ = (2 /3) cos(2 /3) sin(2 /3) 0.5 3 /2, i e ii π = + =− + π π and (4 /3) 0.5 3 /2. i e i π =− −

(b)We see that in(1.36)satisfies *=e=1,so the nth roots of I all have absolute value 1.When k in(1.36)increases by 1,the phase increases by 2/n. 1.29e-e0 cisinc()isin()cos0+isin-(cos0-isin)sin0 2i 2i 2i where(2.14)was used. cos+isin+cos(-0)+isin(-0)cos0+isin+cos-isincos0 2 2 1.30 (a)From f=ma,1N=1 kg m/s2. (b)1J=1kg m2/s2 151F-=-cgw09-0sN 21.602×10-19C)791.602×10-19C) where 2 and 79 are the atomic numbers of He and Au. 1.32(a)4xsin(3x4)+2x212xr3)cos(3x4)=4xsin(3x4)+24x3cos(3x4). (b)(x3+x)=(8+2)-(1+1)-8. 133(a)T,(b)F;(c)F;(dT(e)F,(国T. 1-5 Copyright2014 Pearson Education.Inc
1-5 Copyright © 2014 Pearson Education, Inc. (b) We see that ω in (1.36) satisfies 0 ωω* 1, = e = so the nth roots of 1 all have absolute value 1. When k in (1.36) increases by 1, the phase increases by 2π/n. 1.29 cos sin [cos( ) sin( )] cos sin (cos sin ) 22 2 i i ee i i i i ii i θ θ θ θ θ θ θθθθ − − + − −+ − + − − = = = sin θ, where (2.14) was used. cos sin [cos( ) sin( )] cos sin cos sin 22 2 i i ee i i i i θ θ θ θ θ θ θ θθ θ − + + + −+ − + + − = = = cos θ. 1.30 (a) From , f = ma 1 N = 1 kg m/s2 . (b) 1 J = 1 kg m2 /s2 . 1.31 F = 19 19 1 2 2 12 2 2 13 2 0 2(1.602 10 C)79(1.602 10 C) 4 4 8.854 10 C /N-m )(3.00 10 m) Q Q πε π r − − − − × × = (× × = 0.405 N, where 2 and 79 are the atomic numbers of He and Au. 1.32 (a) 4 23 4 4 5 4 4 sin(3 ) 2 (12 )cos(3 ) 4 sin(3 ) 24 cos(3 ). x x xx x x x x x + =+ (b) 3 2 1 ( ) | (8 2) (1 1) 8. x x + = + −+= 1.33 (a) T; (b) F; (c) F; (d) T; (e) F; (f) T

Chapter 2 The Particle in a Box 2.1 (a)The auxiliary equation is s2+s-6=0 and s=[11+2]/2=2 and-3.So y=ce2x+ce-3x (b)Settingx=0 andy=0,we get 0=c+c (Eq.1).Differentiation of y gives y'=2ce2x-3cze-3x.Settingx=0 and y'=1,we have 1=2c-3c2 (Eq.2).Subtracting twice Eq.I from Eq.2,we get 1=-5c2 and c2=-0.2.Equation 1 then gives c=0.2. 2.2 For y"+py'+qy=0,the auxiliary equation is s2+ps+=0=(s-s)(s-s2).where s and s2 are the roots.Comparison with Eq.(2.8)shows that s=2+i and s2=2-i,so the auxiliary equation is 0=(s-2-1)(s-2+1)=s2-4s+5.Therefore p=-4 and g=5.The differential equation is y"-4y+5y=0. 2.3 (a)The quadratic formula gives the solutions of the [Eq.(2.7)]as s=(pp2-4)/2.To have equal roots of the auxiliary equation requires that p2-4=0.Setting =p2/4 in the differential equation (2.6).we have y+py'+(p2/4)y=0(Eq.1).The auxiliary-equation solution is s=-p/2.Thus we must show that y2=xe is the second solution.Differentiation gives -pxe and=-pepxe/4.Substitution in Eq.(1)gives the left side of Eq.(1)as -pe-2+p2xe-m2/4+pe-2-p2xe-m2 2+p2xe-214. which equals zero and completes the proof. (b)The auxiliary equation s2-2s+1=(s-1)2=0 has rootss=1 and s=1.From part (a),the solution is y=ce*+czxe" 2.4 In comparing Eqs.(1.8)and (2.2),y in(2.2)is replaced by x,and x in(2.2)is replaced by t.Therefore x and its derivatives in (18)must occur to the first power to have a linear differential equation.(a)Linear,(b)linear,(c)nonlinear,(d)nonlinear,(e)linear 2.5 (a)F;(b)F;(c)T;(d)F(only solutions that meet certain conditions such as being continuous are allowed as stationary-state wave functions):(e)T. 2-1 Copyright2014 Pearson Education.Inc
Copyright © 2014 Pearson Education, Inc. 2-1 Chapter 2 The Particle in a Box 2.1 (a) The auxiliary equation is 2 s s + − = 6 0 and s = [ 1 1 24] / 2 2 −± + = and –3. So 2 3 1 2 . x x y ce c e− = + (b) Setting x = 0 and y = 0, we get 1 2 0 = c c + (Eq. 1). Differentiation of y gives 2 3 1 2 2 3. x x y ce c e− ′ = − Setting x = 0 and y′ = 1, we have 1 2 12 3 = c c − (Eq. 2). Subtracting twice Eq. 1 from Eq. 2, we get 2 1 5 = − c and 2 c = −0.2. Equation 1 then gives 1c = 0.2. 2.2 For 0, y py qy ′′ ′ + += the auxiliary equation is 2 1 2 s ps q s s s s + +== − − 0 ( )( ), where 1s and 2s are the roots. Comparison with Eq. (2.8) shows that 1s i = 2 + and 2s i = − 2 , so the auxiliary equation is 2 0 ( 2 )( 2 ) 4 5. = −− −+ = − + s is i s s Therefore p = −4 and q = 5. The differential equation is y yy ′′ ′ − 4 5 0. + = 2.3 (a) The quadratic formula gives the solutions of the auxiliary equation 2 s ps q + += 0 [Eq. (2.7)] as 2 s pp q =− ± − ( 4 ) / 2. To have equal roots of the auxiliary equation requires that 2 p q − = 4 0 . Setting 2 q p = /4 in the differential equation (2.6), we have 2 y py p y ′′ ′ ++ = ( /4) 0 (Eq. 1). The auxiliary-equation solution is s p = − /2. Thus we must show that /2 2 px y xe− = is the second solution. Differentiation gives /2 /2 2 /2 px px y e pxe − − ′ = − and /2 2 /2 2 /4. px px y pe p xe − − ′′ =− + Substitution in Eq. (1) gives the left side of Eq. (1) as /2 2 /2 /2 2 /2 2 /2 /4 /2 /4 px px px px px pe p xe pe p xe p xe −−−− − −+ + − + , which equals zero and completes the proof. (b) The auxiliary equation 2 2 ss s − 2 1 ( 1) 0 += − = has roots s = 1 and s = 1. From part (a), the solution is 1 2 . x x y = + c e c xe 2.4 In comparing Eqs. (1.8) and (2.2), y in (2.2) is replaced by x, and x in (2.2) is replaced by t. Therefore x and its derivatives in (1.8) must occur to the first power to have a linear differential equation. (a) Linear; (b) linear; (c) nonlinear; (d) nonlinear; (e) linear. 2.5 (a) F; (b) F; (c) T; (d) F (only solutions that meet certain conditions such as being continuous are allowed as stationary-state wave functions); (e) T
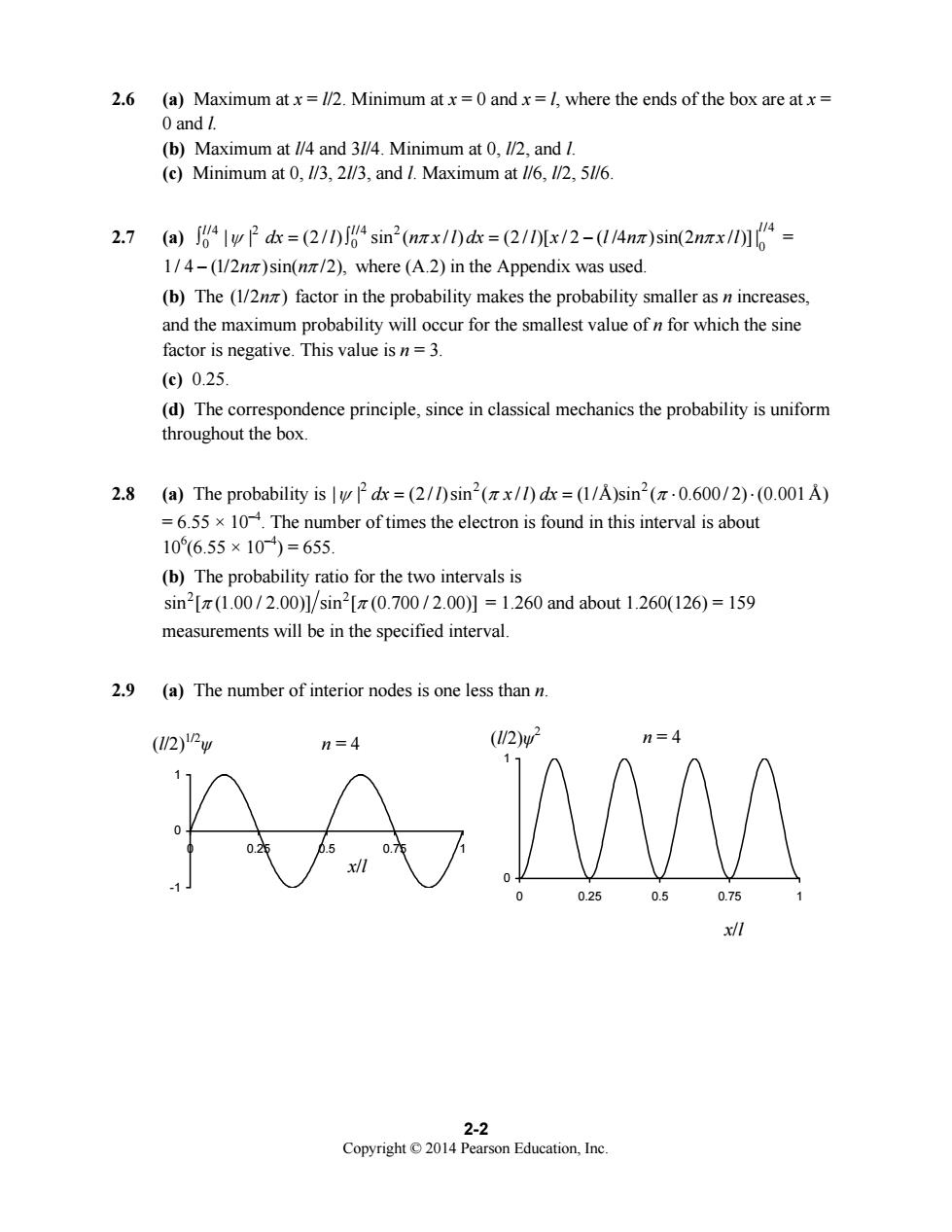
2.6 (a)Maximum at x=1/2.Minimum atx=0 andx=l,where the ends of the box are atx= 0 and (b)Maximum at //4 and 3//4.Minimum at 0,//2,and I. (c)Minimum at /3,2//3,and I.Maximum at /6,5//6 2.7(a))4|w2dk=(2/0Jsin2(nrx/0dr=(2/I0[x/2-(14nz)sin(2nrx/]4= 1/4-(1/2)sin(nz/2),where(A.2)in the Appendix was used (b)The (1/)factor in the probability makes the probability smaller asn increases. and the maximum probability will occur for the smallest value of n for which the sine factor is negative.This value is n=3. (c90.25 (d)The correspondence principle,since in classical mechanics the probability is uniform throughout the box. 2.8 (a)The probability isdx=(2/1)sin2(x/)dx=(1/A)sin2(0.600/2)-(0.001A) =6.55 x 10.The number of times the electron is found in this interval is about 10(6.55×10)=655. (b)The probability ratio for the two intervals is sin2[π(1.00/2.00]/sin2[π(0.700/2.00)】=1.260 and about1.260(126)=159 measurements will be in the specified interval. 2.9 (a)The number of interior nodes is one less than n. (2)Pw (2 2-2 Copyright2014 Pearson Education.Inc
Copyright © 2014 Pearson Education, Inc. 2-2 2.6 (a) Maximum at x = l/2. Minimum at x = 0 and x = l, where the ends of the box are at x = 0 and l. (b) Maximum at l/4 and 3l/4. Minimum at 0, l/2, and l. (c) Minimum at 0, l/3, 2l/3, and l. Maximum at l/6, l/2, 5l/6. 2.7 (a) /4 2 /4 2 /4 0 0 0 | | (2 / ) sin ( / ) (2 / )[ / 2 ( /4 )sin(2 / )] |l l l ∫ =∫ = − ψ π ππ dx l n x l dx l x l n n x l = 1/ 4 (1/2 )sin( /2), − n n π π where (A.2) in the Appendix was used. (b) The (1/2 ) nπ factor in the probability makes the probability smaller as n increases, and the maximum probability will occur for the smallest value of n for which the sine factor is negative. This value is n = 3. (c) 0.25. (d) The correspondence principle, since in classical mechanics the probability is uniform throughout the box. 2.8 (a) The probability is 22 2 | | (2 / )sin ( / ) (1/Å)sin ( 0.600 / 2) (0.001 Å) ψπ π dx l x l dx = = ⋅⋅ = 6.55 × 10–4. The number of times the electron is found in this interval is about 106 (6.55 × 10–4) = 655. (b) The probability ratio for the two intervals is 2 2 sin [ (1.00 / 2.00)] sin [ (0.700 / 2.00)] π π = 1.260 and about 1.260(126) = 159 measurements will be in the specified interval. 2.9 (a) The number of interior nodes is one less than n. -1 0 1 0 0.25 0.5 0.75 1 0 1 0 0.25 0.5 0.75 1 (l/2) n = 4 1/2 ψ x/l n = 4 x/l (l/2)ψ 2
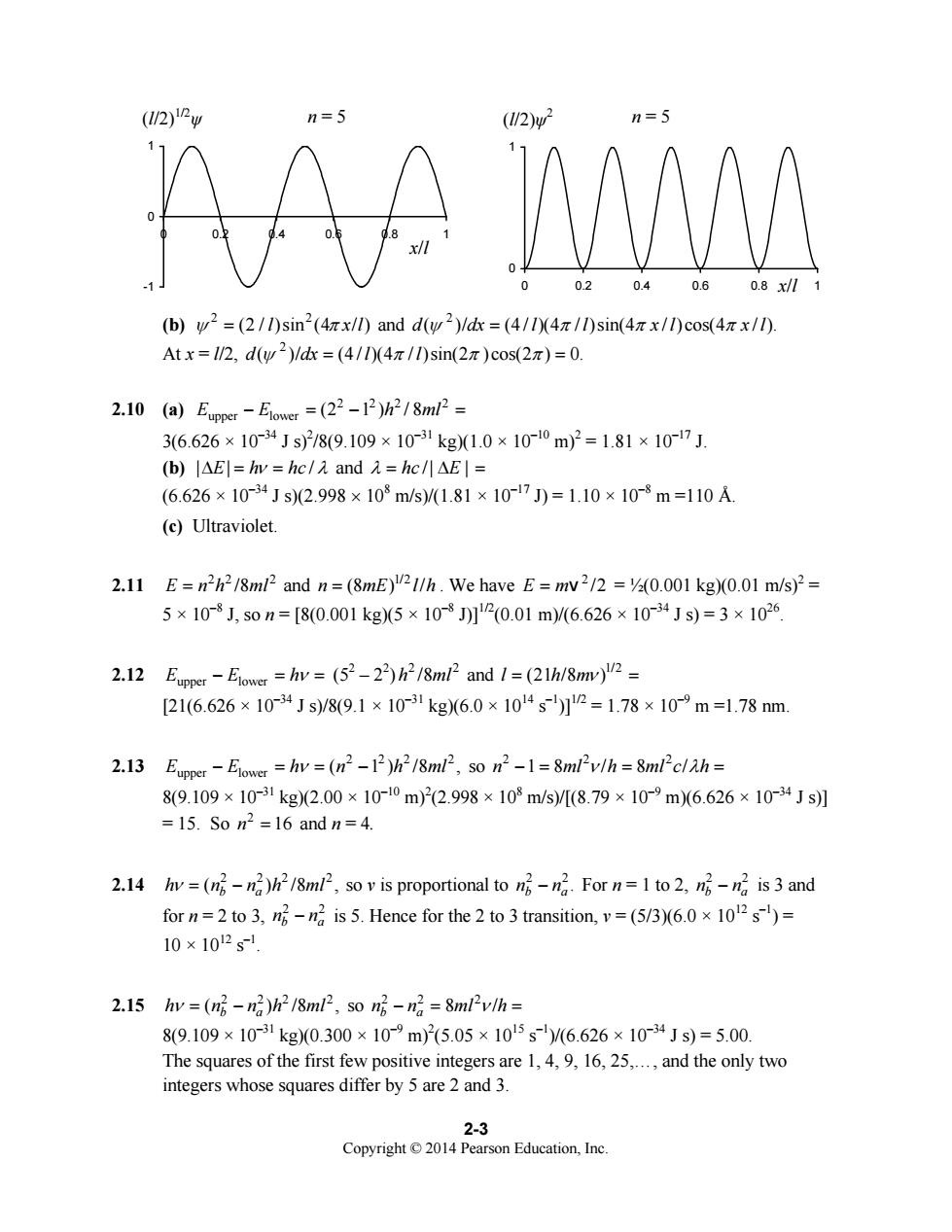
(12)w (/2)w2 n=5 品 08/ (b)w2=(2/1)sin2(4zx/l)and d(w2)/dx=(4/1(4/1)sin(4 x/l)cos(4x/1). Atx=1/2,dw2)/dk=(41I0(4π/0sin(2π)cos(2x)=0. 2.10(al)Eme-Eoe=(22-1P18ml2= 36.626×10-34Js2/8(9.109×10-31kg1.0×10-0m)2=1.81×10-17J. (b)l△El=hw=hc/aand2=hc/I△El= (6.626×10-34Js(2.998×103m/s)/1.81×1017J)=1.10×10-3m=110A (c)Ultraviolet. 2.11 E=n2h2/8ml2 and n=(8mE)2I/h.We have E=mv2/2 =(0.001 kg)(0.01 m/s)2= 5×10-8J,s0n=[8(0.001kg5×10-8J2(0.01m)/6.626×10~34Js)=3×1026 2.12Eper-Elower=hv=(52-2)h2/8m2and1=(21h/8m)2= [21(6.626×1034Js)/8(9.1×10-1kg6.0×1014s]2=1.78×10m=1.78nm 2.13 Euppe:-Elower=hv=(nh218ml2,so n2-1=8mlv/h=8mlclah= 8(9.109×10-31kg(2.00×1010m)2(2.998×108m/s)/(8.79×10m)6.626×10-34Js】 =15.S0m2-16andn=4. 2.14 hv =(np-n2)h2/8ml2,so v is proportional to nng.For n=I to 2.mn is 3 and for n=2 to 3.n is 5.Hence for the 2 to 3 transition,v=(5/3)(6.0x 102s)= 10×102s- 2.15 hy =(np-n2)h2 /8ml2,so np-n2 8ml2v/h 89.109×10-1kg0.300×109m)5.05×105s)/6.626×1034Js)=5.00. The squares of the first few positive integers are 1,4,9,16,25,.and the only two integers whose squares differ by 5 are 2 and 3 2-3 Education.Inc
Copyright © 2014 Pearson Education, Inc. 2-3 -1 0 1 0 0.2 0.4 0.6 0.8 1 0 1 0 0.2 0.4 0.6 0.8 1 (b) 2 2 ψ = (2 / )sin (4 / ) l xl π and 2 d dx l l x l x l ( )/ (4 / )(4 / )sin(4 / )cos(4 / ). ψ ππ π = At x = l/2, 2 d dx l l ( )/ (4 / )(4 / )sin(2 )cos(2 ) 0. ψ π ππ = = 2.10 (a) 2 22 2 upper lower E E h ml − =− = (2 1 ) / 8 3(6.626 × 10–34 J s)2 /8(9.109 × 10–31 kg)(1.0 × 10–10 m)2 = 1.81 × 10–17 J. (b) || / Δ= = E h hc ν λ and /| | λ = hc EΔ = (6.626 × 10–34 J s)(2.998 × 108 m/s)/(1.81 × 10–17 J) = 1.10 × 10–8 m =110 Å. (c) Ultraviolet. 2.11 22 2 E n h ml = /8 and 1/2 n mE l h = (8 ) / . We have 2 E m= v /2 = ½(0.001 kg)(0.01 m/s)2 = 5 × 10–8 J, so n = [8(0.001 kg)(5 × 10–8 J)]1/2(0.01 m)/(6.626 × 10–34 J s) = 3 × 1026. 2.12 EEh upper lower − == ν (52 – 22 ) 2 2 h ml /8 and 1/2 l hm = (21 /8 ) ν = [21(6.626 × 10–34 J s)/8(9.1 × 10–31 kg)(6.0 × 1014 s–1)]1/2 = 1.78 × 10–9 m =1.78 nm. 2.13 2 22 2 upper lower E E h n h ml − == − ν ( 1 ) /8 , so 22 2 n ml h ml c h −18 / 8 / == = ν λ 8(9.109 × 10–31 kg)(2.00 × 10–10 m)2 (2.998 × 108 m/s)/[(8.79 × 10–9 m)(6.626 × 10–34 J s)] = 15. So 2 n = 16 and n = 4. 2.14 2 22 2 ( ) /8 , b a h n n h ml ν = − so ν is proportional to 2 2. b a n n − For n = 1 to 2, 2 2 b a n n − is 3 and for n = 2 to 3, 2 2 b a n n − is 5. Hence for the 2 to 3 transition, ν = (5/3)(6.0 × 1012 s–1) = 10 × 1012 s–1. 2.15 2 22 2 ( ) /8 , b a h n n h ml ν = − so 22 2 8 / b a n n ml h − = = ν 8(9.109 × 10–31 kg)(0.300 × 10–9 m)2 (5.05 × 1015 s–1)/(6.626 × 10–34 J s) = 5.00. The squares of the first few positive integers are 1, 4, 9, 16, 25,., and the only two integers whose squares differ by 5 are 2 and 3. n = 5 (l/2)ψ n = 5 2 (l/2)1/2 ψ x/l x/l

2.16v=h(Eupper -Elower)=h(h2/8ml2)(n-m)=(h/8ml2)k,where k is an integer For n=1 and n=1,2.3.we get the following k values: k=22-12=3k=32-22=5k=42-32=7,k=9,11,13,15,tc For n-n =3 and n =1,2,3.we get k=42-12=15,k=52-22=21k=62-32=27,k=33,39,tc For n -n=5 and n=1,2.3.,we get k=35,45,55,etc. The smallest k that corresponds to two different transitions is k=15 for the I to 4 transition and the 7 to 8 transition 2.17 Each double bond consists of one sigma and one pi bond,so the two double bonds have 4 pi electrons.With two pi electrons in each particle-in-a-box level,the 4 pi electrons occupy the lowest two levels,n=1 and n=2.The highest-occupied to lowest-vacant transition is from n=2 to n=3,so AEl=hv hc/=(32-22)h2/8ml2 and A.8m.s9109x10"kgX70x1o0m2298x10m的-32x107m= 5h 56.626×1034Js) 320nm 2.18 Outside the box,=0.Inside the box,w is given by (2.15)as =acos[(2mE)x]+bsin[h(2mE)x]Continuity requires that =0at x=-112 and at x=1/2,the left and right ends of the box.Using (2.14),we thus have 0=acos[h'(2mE)21/2]-bsin[h'(2mE)21/2]Eq.(1] 0=acos[h'(2mE)21/2]+bsim[h'(2mE)21/2]Eq.(2l Adding Eqs.(1)and(2)and dividing by 2,we get 0=acos[h(2mE)21/2].so either a=0 or cos[h(2mE)21/]=0 [Eq.(3)] Subtracting Eq.(1)from(2)and dividing by 2.we get =bsin[h(2mE)21/].so either b=0 or sin[h (2mE)1/]=0 [Eq.(4)]. If a=0,then b cannot be 0(because this would make =0),so ifa=0,then sin[h-(2mE)21]=0 [Eq.(5)]and w=bsin[h(2mE)2x].To satisfy Eq.(5).we must have [(2mE)1]=k where k is an integer.The wave functions and energies when a=0 are yw=bsin2kπx/l川andE=(2k)2h2/8ml2,wherek=1,2,3,.Eq.(6】 (For reasons discussed in Chapter2,not allowed and negative values of k do not give a different w.) 24 Copyright2014 Pearson Education.Inc
Copyright © 2014 Pearson Education, Inc. 2-4 2.16 1 12 2 2 2 2 upper lower ( ) ( /8 )( ) ( /8 ) , u ν h E E h h ml n n h ml k − − = − = −= A where k is an integer. For 1 u n n − =A and 1, 2, 3, , nA = . we get the following k values: 22 2 2 2 2 kk k k = −= = − = = − = = 2 1 3; 3 2 5; 4 3 7; 9,11,13,15, etc. For 3 u n n − =A and 1, 2, 3, , nA = . we get 22 2 2 k k = −= = − = 4 1 15; 5 2 21; 2 2 k k =−= = 6 3 27; 33, 39, etc. For 5 u n n − =A and 1, 2, 3, , nA = . we get k = 35, 45, 55, etc. The smallest k that corresponds to two different transitions is k = 15 for the 1 to 4 transition and the 7 to 8 transition. 2.17 Each double bond consists of one sigma and one pi bond, so the two double bonds have 4 pi electrons. With two pi electrons in each particle-in-a-box level, the 4 pi electrons occupy the lowest two levels, n = 1 and n = 2. The highest-occupied to lowest-vacant transition is from n = 2 to n = 3, so 2 22 2 | | / (3 2 ) /8 Δ= = = − E h hc h ml ν λ and 2 31 10 2 8 34 8 8(9.109 10 kg)(7.0 10 m) (2.998 10 m/s) 5 5(6.626 10 J s) ml c h λ − − − ×× × = = × = 7 3.2 10 m − × = 320 nm 2.18 Outside the box, 0. ψ = Inside the box, ψ is given by (2.15) as 1 1/2 1 1/2 ψ a mE x b mE x cos[ (2 ) ] sin[ (2 ) ]. − − = + = = Continuity requires that ψ = 0 at x = −l/2 and at x = l/2, the left and right ends of the box. Using (2.14), we thus have 1 1/2 1 1/2 0 cos[ (2 ) /2] sin[ (2 ) /2] a mE l b mE l − − = − = = [Eq. (1)] 1 1/2 1 1/2 0 cos[ (2 ) /2] sin[ (2 ) /2] a mE l b mE l − − = + = = [Eq. (2)]. Adding Eqs. (1) and (2) and dividing by 2, we get 1 1/2 0 cos[ (2 ) /2], a mE l − = = so either a = 0 or 1 1/2 cos[ (2 ) /2] 0 mE l − = = [Eq. (3)]. Subtracting Eq. (1) from (2) and dividing by 2, we get 1 1/2 0 sin[ (2 ) /2], b mE l − = = so either b = 0 or 1 1/2 sin[ (2 ) /2] 0 mE l − = = [Eq. (4)]. If a = 0, then b cannot be 0 (because this would make ψ = 0), so if a = 0, then 1 1/2 sin[ (2 ) /2] 0 mE l − = = [Eq. (5)] and 1 1/2 ψ b mE x sin[ (2 ) ]. − = = To satisfy Eq. (5), we must have 1 1/2 [ (2 ) /2] , mE l kπ − = = where k is an integer. The wave functions and energies when a = 0 are sin[2 / ] ψ = b k xl π and 22 2 E k h ml = (2 ) /8 , where k = 1, 2, 3,. [Eq. (6)] (For reasons discussed in Chapter 2, k = 0 is not allowed and negative values of k do not give a different ψ.)

If b=0.then a cannot be (because this would make=0).so ifb=0.then cos(2m]=0[Eq.(7)and acos(2mE)x]To satisfy Eq.()we must have [(2mE)21/2]=(2j+1/2.where jis an integer.The wave functions and energies when b=0 are w=acos[(2j+1)xx/I]and E=(2j+1)h2/8ml2,wherej=0,1,2,3.[Eq.(8)] (As discussed in Chapter 2,negative values ofjdo not give a different.) In Eq.(8),j+I takes on the values 1,3,5.in Eq.(6),2k takes on the values 2.4,6.Therefore E=n2h2/8ml2,where n=1,2,3.,as we found with the origin at the left end of the box.Also,the wave functions in Eqs.(6)and(8)are the same as with the origin at the left end,as can be verified by sketching a few of them 2.19 Using square brackets to denote the dimensions of a quantity and M.L.Tto denote the s,length,and time.we have []ML[ML In order to have the same dimensions on each side of the equation,the powers of M.L,and T must match.o1+2+c. We geta=2.b=1-a=-1,andc=2-2a=-2. 2.0 From Eqs.(120)and (20).() 2.21 (a)Let r=(2m/h2)2Vo-E)2 and s=(2m/h2)E2.Then w=Ce and Wu Acossx+Bsin sx.We have wi=Cre and wi =-sAsin sx+sBcos sx.The condition wi(0=wi(0)gives Cr=sB,so B=Cr/s=Ar/s=A(Vo-E)2/E2,since C=A,as noted a few lines before Eq.(2.33). (b)wm =Ge and win =-rGe.From(a).wi =-sAsin sx+s(Ar/s)cossx.The relations wi()=i (and wn()=wm(1)give-sAsinsl+rAcossl=-rGe-and Acossl+(Ar/s)sinsl=Ge Dividing the first equation by the second,we get -ssins/+rcossl cossl+rssinsl =rand 2rscoss/=(s2-r2)sinsl.Substitution for rand s gives 2(2m/h2)(VoE-E2)2 cos[(2mE)]=(2m/h2(2E-Vo)sin[(2mE)2I/h],which is (2.33) 2.22 (a)As o 2E on the left side of (2.33)can be neglected compared with Vo,and on the right side can be neglected to give tan[(2mE)]=-2(VE)= 2(E/V).The right side of this equation goes toas so tan[(2mE)/=0.This equation is satisfied when (2mE)2I/h=nz,where n is an 2-5 Education.Inc
Copyright © 2014 Pearson Education, Inc. 2-5 If b = 0, then a cannot be 0 (because this would make ψ = 0), so if b = 0, then 1 1/2 cos[ (2 ) / 2] 0 mE l − = = [Eq. (7)] and 1 1/2 ψ a mE x cos[ (2 ) ]. − = = To satisfy Eq. (7), we must have 1 1/2 [ (2 ) / 2] (2 1) /2, mE l j π − = = + where j is an integer. The wave functions and energies when b = 0 are ψ = + a j xl cos[(2 1) / ] π and 22 2 E = + (2 1) / 8 j h ml , where j = 0, 1, 2, 3,. [Eq. (8)] (As discussed in Chapter 2, negative values of j do not give a different ψ.) In Eq. (8), 2j + 1 takes on the values 1, 3, 5,.; in Eq. (6), 2k takes on the values 2, 4, 6,. . Therefore 22 2 E = n h ml /8 , where n = 1, 2, 3,., as we found with the origin at the left end of the box. Also, the wave functions in Eqs. (6) and (8) are the same as with the origin at the left end, as can be verified by sketching a few of them. 2.19 Using square brackets to denote the dimensions of a quantity and M, L, T to denote the dimensions mass, length, and time, we have [E] = ML2 T–2 = [h] a [m] b [l] c = [E] a T a Mb L c = (ML2 T–2) a T a Mb L c = Ma+bL 2a+cT–a. In order to have the same dimensions on each side of the equation, the powers of M, L, and T must match. So 1 = a + b, 2 = 2a + c, –2 = –a. We get a = 2, b = 1 – a = –1, and c = 2 – 2a = –2. 2.20 From Eqs. (1.20) and (2.30), 1/2 1/2 / (2 ) / (2 ) / 1 2 ( ) iEt i mE x i mE x e ce c e − − Ψ= + == = . 2.21 (a) Let 2 1/2 1/2 0 r m VE ≡ − (2 / ) ( ) = and 2 1/2 1/2 sm E ≡ (2 / ) = . Then I rx ψ = Ce and II ψ = + A sx B sx cos sin . We have I rx ψ′ = Cre and II ψ′ = − + sA sx sB sx sin cos . The condition I II ψ′ ′ (0) (0) =ψ gives Cr sB = , so 1/2 1/2 0 B ===− Cr s Ar s A V E E / / ( )/ , since C = A, as noted a few lines before Eq. (2.33). (b) III rx ψ Ge− = and III . rx ψ rGe− ′ = − From (a), II ψ′ = − + sA sx s Ar s sx sin ( / )cos . The relations II III ψ′ ′′ () () l l =ψ and II III ψ () () l l =ψ give sin cos rl sA sl rA sl rGe− − + =− and cos ( / )sin . rl A sl Ar s sl Ge− + = Dividing the first equation by the second, we get 1 sin cos cos sin s sl r sl r sl rs sl − − + = − + and 2 2 2 cos ( )sin . rs sl s r sl = − Substitution for r and s gives 2 2 1/2 1/2 2 1/2 0 0 2(2 / )( ) cos[(2 ) / ] (2 / )(2 )sin[(2 ) / ] m V E E mE l m E V mE l = == = − =− , which is (2.33). 2.22 (a) As 0 V → ∞, 2E on the left side of (2.33) can be neglected compared with V0, and E2 on the right side can be neglected to give 1/2 1/2 0 0 tan[(2 ) / ] 2( ) / mE l V E V = = − = 1/2 0 −2( / ) . E V The right side of this equation goes to 0 as 0 V → ∞, so 1/2 tan[(2 ) / ] 0. mE l = = This equation is satisfied when 1/2 (2 ) / , mE l n = = π where n is an