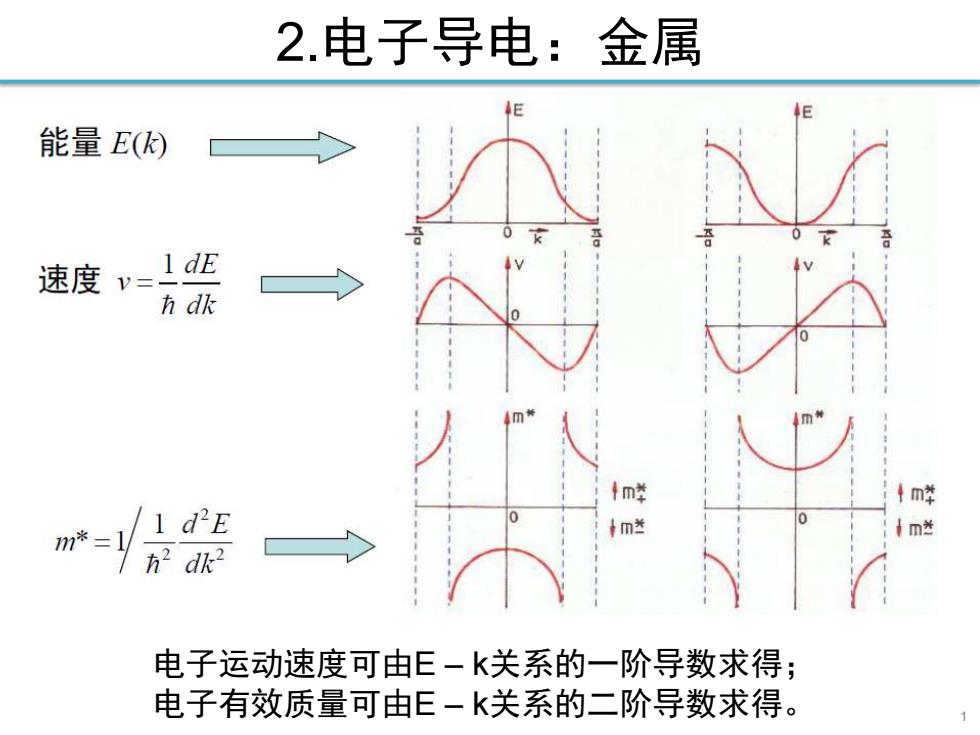
2.电子导电:金属 能量E() 速度v=l近 方dk m¥ 1m¥ m*=1 1 dE tm m dk? 电子运动速度可由E-k关系的一阶导数求得; 电子有效质量可由E-k关系的二阶导数求得
2.电子导电:金属 1 电子运动速度可由E – k关系的一阶导数求得; 电子有效质量可由E – k关系的二阶导数求得
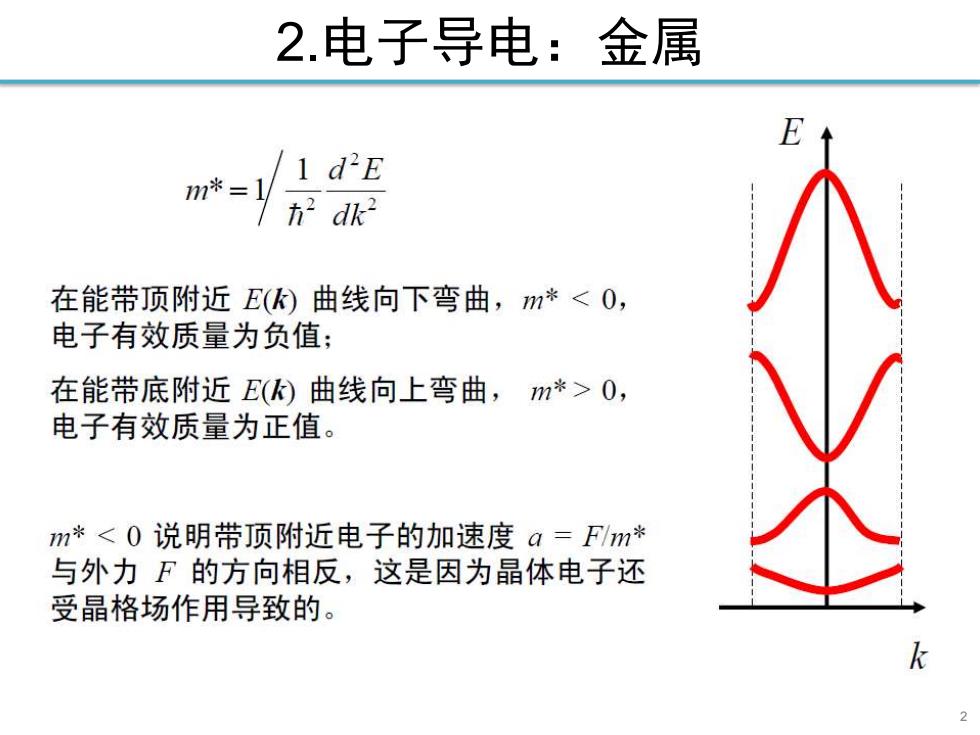
2.电子导电:金属 m*=1儿 1 dE h dk? 在能带顶附近E()曲线向下弯曲,m*0, 电子有效质量为正值。 m*<0说明带顶附近电子的加速度a=F/m* 与外力F的方向相反,这是因为晶体电子还 受晶格场作用导致的
2 2.电子导电:金属

2.电子导电:金属 有了有效质量m*这一便利的数学工具以后,立刻就可以仿照自由电子迁移 率(Drude模型)的求法,算出晶格场中电子的迁移率 e elF m* m*VE e:电子电荷, T: 电子弛豫时间 VE: 费米速度 l:费米面附近电子的平均自由程 并且,由此可以得出电导率的表达式: o =nefeu m*VE ner:单位体积内有效电子(处于未满能带中实际参与导电的电子)的数量
3 2.电子导电:金属 有了有效质量m*这一便利的数学工具以后,立刻就可以仿照自由电子迁移 率(Drude模型)的求法,算出晶格场中电子的迁移率 𝜇 = 𝑒𝜏 𝑚∗ = 𝑒𝑙𝐹 𝑚∗𝑣𝐹 e: 电子电荷, : 电子弛豫时间 vF:费米速度 lF:费米面附近电子的平均自由程 并且,由此可以得出电导率的表达式: 𝜎 = 𝑛𝑒𝑓𝑒𝜇 = 𝑛𝑒𝑓𝑒 2 𝑙𝐹 𝑚∗𝑣𝐹 nef:单位体积内有效电子(处于未满能带中实际参与导电的电子)的数量
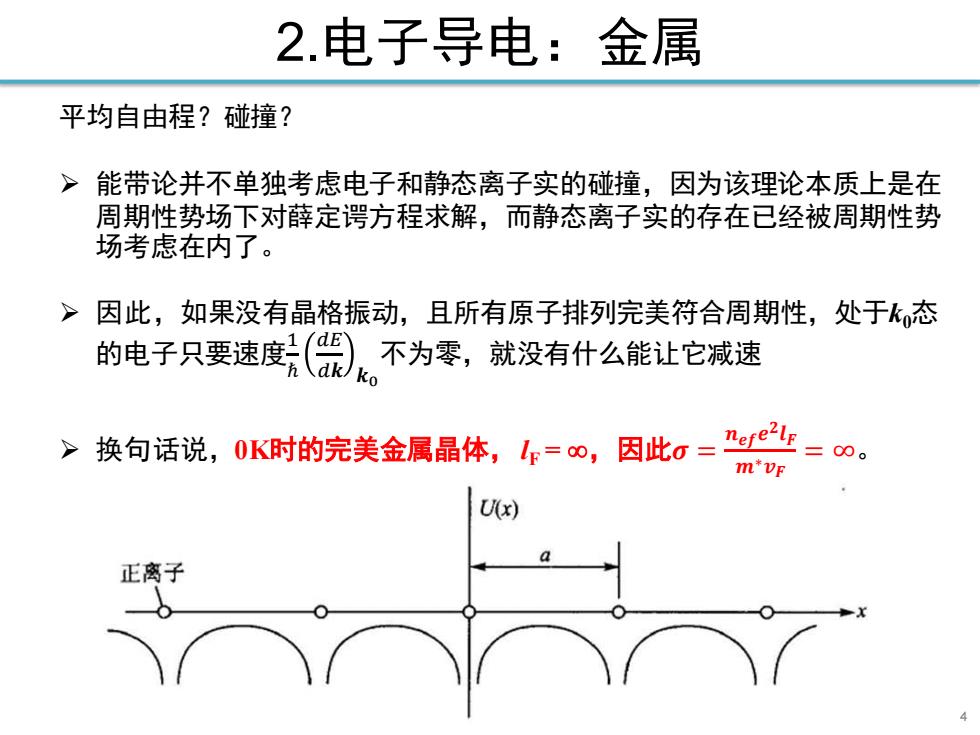
2.电子导电:金属 平均自由程?碰撞? >能带论并不单独考虑电子和静态离子实的碰撞,因为该理论本质上是在 周期性势场下对薛定谔方程求解,而静态离子实的存在已经被周期性势 场考虑在内了。 >因此,如果没有晶格振动,且所有原子排列完美符合周期性,处于k态 的电子只要速度() dk ko 不为零,就没有什么能让它减速 >换句话说,0K时的完美金属晶体,1=∞,因此o=”r=0。 m*vF U(x) 正离子
4 2.电子导电:金属 平均自由程?碰撞? ➢ 能带论并不单独考虑电子和静态离子实的碰撞,因为该理论本质上是在 周期性势场下对薛定谔方程求解,而静态离子实的存在已经被周期性势 场考虑在内了。 ➢ 因此,如果没有晶格振动,且所有原子排列完美符合周期性,处于k0态 的电子只要速度1 ℏ 𝑑𝐸 𝑑𝒌 𝒌0 不为零,就没有什么能让它减速 ➢ 换句话说,0K时的完美金属晶体,lF = ,因此𝝈 = 𝒏𝒆𝒇𝒆 𝟐𝒍𝑭 𝒎∗𝒗𝑭 = ∞

2.电子导电:金属 >在晶体晶格完整性受到破坏时,电子才受到散射; >晶格完整性主要可被两方面因素破坏 ·离子振动:仅在T>0K时发生,使离子偏离构成 完美周期性的平衡位置; ·缺陷:异质原子、点缺陷、位错,等等; >电子受到的散射可以由散射系数描述 1 m*vFu m*VE nere2 其中μ=1/l称为散射系数
2.电子导电:金属 5 ➢ 在晶体晶格完整性受到破坏时,电子才受到散射; ➢ 晶格完整性主要可被两方面因素破坏 • 离子振动:仅在T > 0 K时发生,使离子偏离构成 完美周期性的平衡位置; • 缺陷:异质原子、点缺陷、位错,等等; ➢ 电子受到的散射可以由散射系数描述 其中 = 1/lF 称为散射系数 𝜎 = 𝑛𝑒𝑓𝑒 2 𝑙𝐹 𝑚∗𝑣𝐹 𝜌 = 1 𝜎 = 𝑚∗𝑣𝐹𝜇 𝑛𝑒𝑓𝑒 2

2.电子导电:金属 散射系数由两部分组成: L=uT+△W ·4:反映晶格振动对电子的散射,:心温度 ·△:反映缺陷对电子的散射,△4∝缺陷浓度 根据电阻率p= m"VFu 可以相应的得到 P=PL(T)+p' 以上关系式被称为马西森定则 ·P虹⑩被称为本征电阻率,p被称为剩余电阻率 ·高温时,金属的电阻主要由PT项主导;在低温时,p'是主要的; 。 在极低温度(一般为4.2K)下测得的金属电阻率被认为接近剩余电阻率
2.电子导电:金属 6 散射系数由两部分组成: • T:反映晶格振动对电子的散射, T 温度 • :反映缺陷对电子的散射, 缺陷浓度 • 以上关系式被称为马西森定则 • ρL (T)被称为本征电阻率,ρ′被称为剩余电阻率 • 高温时, 金属的电阻主要由ρL (T) 项主导;在低温时,ρ′是主要的; • 在极低温度( 一般为4.2K) 下测得的金属电阻率被认为接近剩余电阻率 根据电阻率𝜌 = 𝑚∗𝑣𝐹𝜇 𝑛𝑒𝑓𝑒 2 ,可以相应的得到 𝜇 = 𝜇𝑇 + ∆𝜇 𝜌 = 𝜌𝐿 𝑇 + 𝜌′
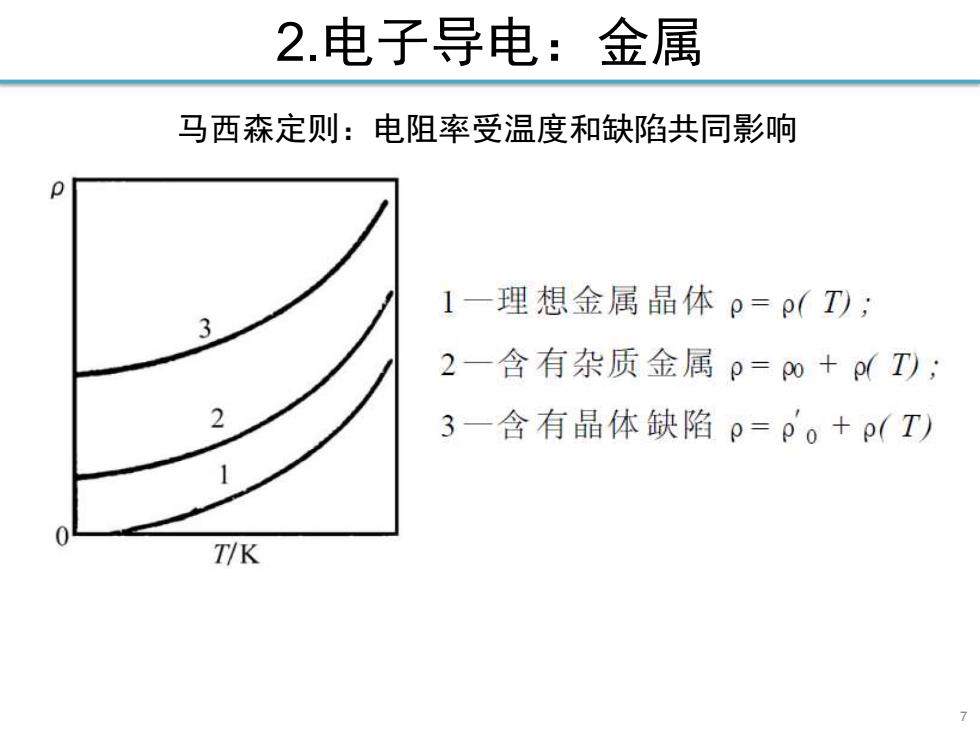
2.电子导电:金属 马西森定则:电阻率受温度和缺陷共同影响 p 1一理想金属晶体p=p(T); 3 2一含有杂质金属p=p0+p(T); 2 3一含有晶体缺陷p=p。+p(T) 1 T/K
2.电子导电:金属 7 马西森定则:电阻率受温度和缺陷共同影响

2.电子导电:金属 ·马西森是谁? Augustus Matthiessen 英国化学家和物理学家; 1831年1月出生于英国富商家庭;幼年时患麻痹性癫痫,导致右手残疾; 1852年获得博士学位(德国吉森大学),21岁; 1857年独立领导实验室工作(英国皇家化学学院),26岁; 1861年荣膺英国皇家化学院会士,30岁; 19世纪60年代:和西门子关于电阻标准产生激烈的公开争执,并一度上 升到对西门子的人身攻击;后者对此给予礼貌回应; 1870年自杀身亡(severe nervous strain),39岁。 主要学术贡献: 分离出锂、钙、锶等元素 确定了近200种合金的电导率、密度等物理性能 马西森定则
2.电子导电:金属 • 马西森是谁? 8 Augustus Matthiessen 英国化学家和物理学家; 1831年1月出生于英国富商家庭;幼年时患麻痹性癫痫,导致右手残疾; 1852年获得博士学位(德国吉森大学),21岁; 1857年独立领导实验室工作(英国皇家化学学院),26岁; 1861年荣膺英国皇家化学院会士,30岁; 19世纪60年代:和西门子关于电阻标准产生激烈的公开争执,并一度上 升到对西门子的人身攻击;后者对此给予礼貌回应; 1870年自杀身亡(severe nervous strain),39岁。 主要学术贡献: 分离出锂、钙、锶等元素 确定了近200种合金的电导率、密度等物理性能 马西森定则

2.电子导电:金属 3.1电阻率与温度的关系 若以P和p表示金属在0℃和T℃下的电阻率,则它们在一定的温 度范围内符合一个经验定律: Pr Po(1+aT) (在温度高于室温情况下,适用于大多数金属) ·其中被称为“平均温度系数”,单位是1C 。 除过渡族金属外,所有纯金属的电阻率平均温度系数近似等于 4×1031/°C 过渡族金属,特别是铁磁性金属具有较高的a值:铁为6.5×1031°℃, 钴为6.0×1031/C,镍为6.9×1031/C 根据温度系数的精确定义(每升高1度引起的电阻率变化比例),其应 表达为 1 dpr 0T= (1/C) (更精确的看,温度系 PT dT 数也是温度的函数。) 9
2.电子导电:金属 9 若以ρ0 和ρT表示金属在 0 ℃ 和 T ℃下的电阻率,则它们在一定的温 度范围内符合一个经验定律: (在温度高于室温情况下,适用于大多数金属) 3.1电阻率与温度的关系 根据温度系数的精确定义(每升高1度引起的电阻率变化比例),其应 表达为 • 其中𝛼ത被称为“平均温度系数”,单位是1/C • 除过渡族金属外,所有纯金属的电阻率平均温度系数近似等于 4×10-3 1/C • 过渡族金属,特别是铁磁性金属具有较高的𝛼ത值: 铁为6.5×10-3 1/C, 钴为6.0×10-3 1/C, 镍为6.9×10-3 1/C (更精确的看,温度系 数也是温度的函数。) 𝜌𝑇 = 𝜌0 (1 + 𝛼ത𝑇) 𝛼𝑇 = 1 𝜌𝑇 𝑑𝜌𝑇 𝑑𝑇 (1/℃)
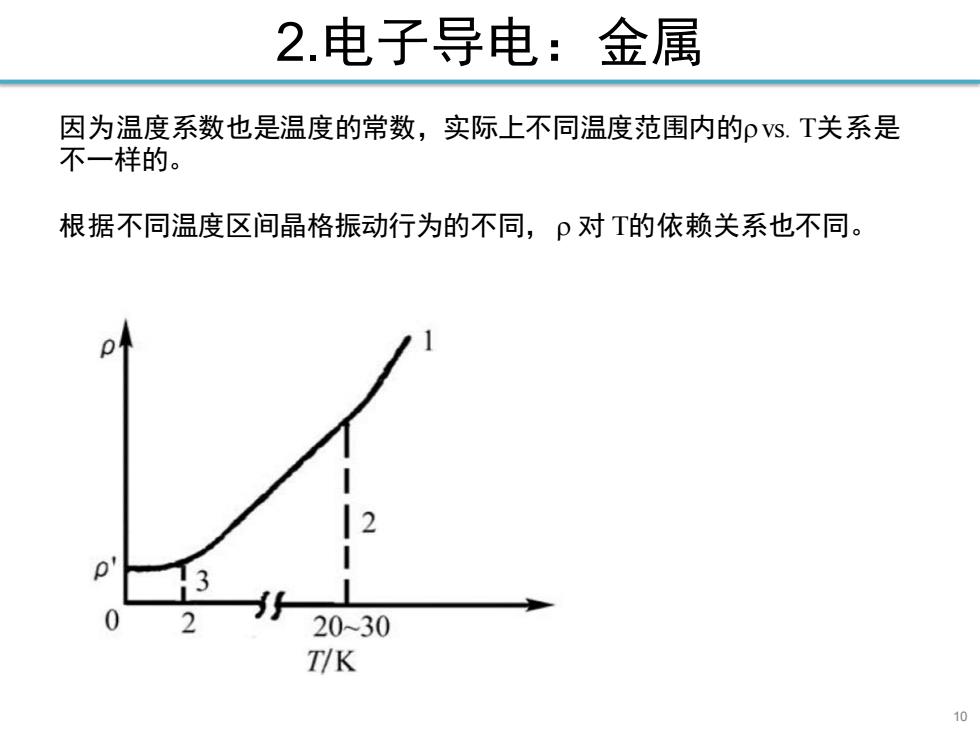
2.电子导电:金属 因为温度系数也是温度的常数,实际上不同温度范围内的pVs.T关系是 不一样的。 根据不同温度区间晶格振动行为的不同,P对T的依赖关系也不同。 2 2 2030 T/K 10
2.电子导电:金属 10 因为温度系数也是温度的常数,实际上不同温度范围内的vs. T关系是 不一样的。 根据不同温度区间晶格振动行为的不同, 对 T的依赖关系也不同