
第七章光的量子性 黑体辐射 光电效应 康普顿散射
第七章 光的量子性 黑体辐射 光电效应 康普顿散射
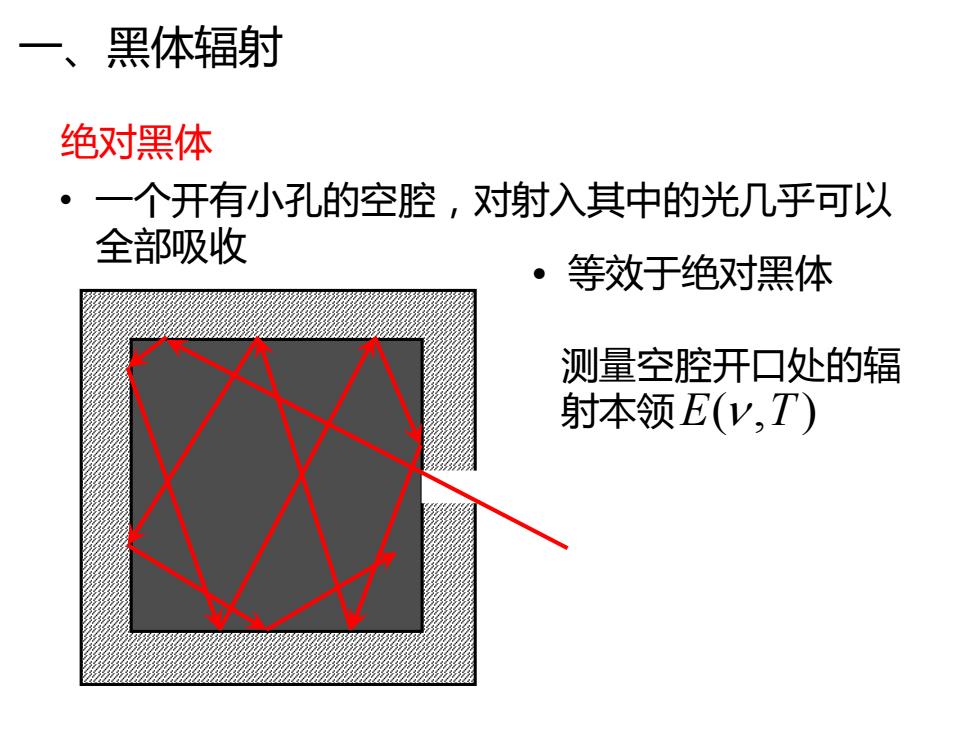
一、黑体辐射 绝对黑体 ·一个开有小孔的空腔,对射入其中的光几乎可以 全部吸收 ·等效于绝对黑体 测量空腔开口处的辐 射本领E(V,T)
绝对黑体 • 一个开有小孔的空腔,对射入其中的光几乎可以 全部吸收 • 等效于绝对黑体 E T ( , ) 测量空腔开口处的辐 射本领 一、黑体辐射
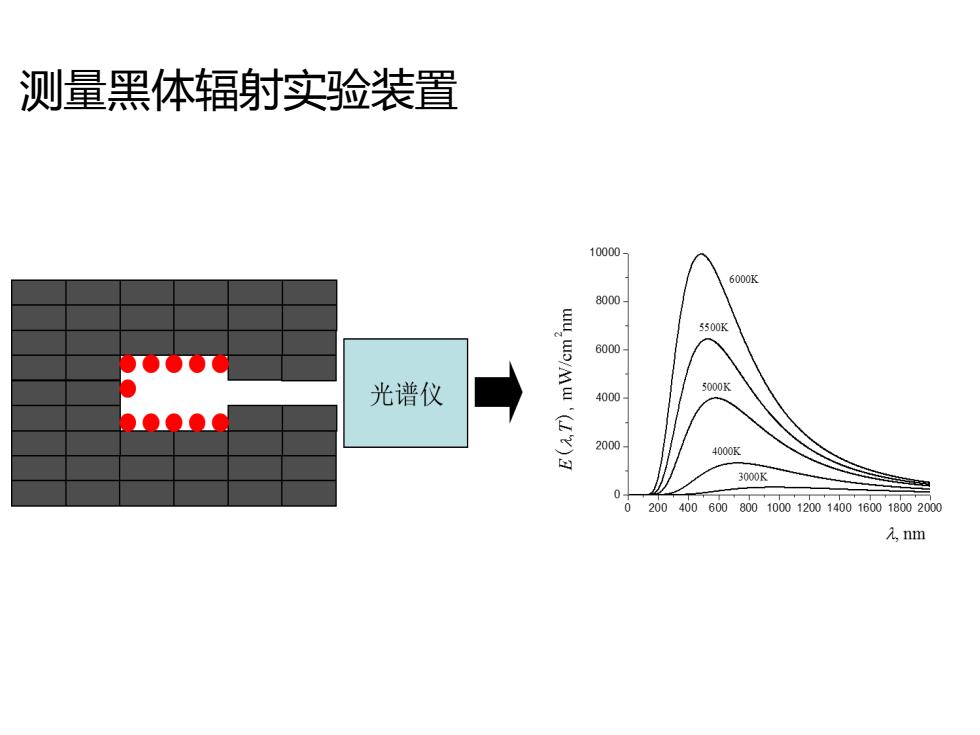
测量黑体辐射实验装置 10000 6000K 8000 5500K 6000 光谱仪 5000K 4000 2000 4000K 3000K 0 0200400600800100012001400160018002000 元,nm
测量黑体辐射实验装置
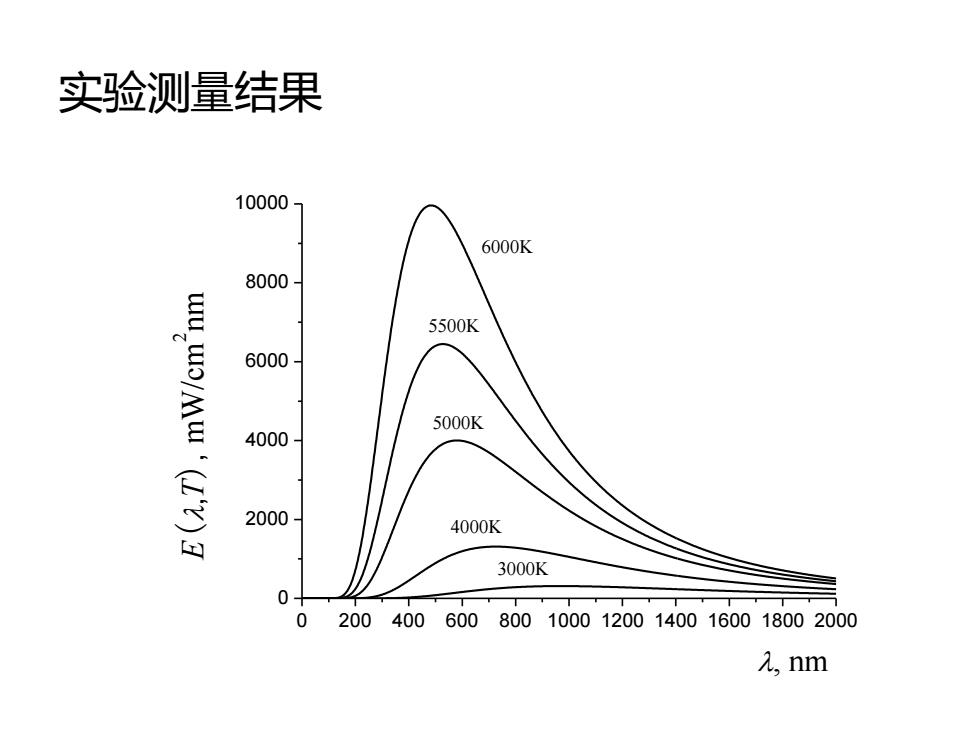
实验测量结果 100007 6000K 8000- 11000Mn 5500K 6000 5000K 4000 2000 4000K 3000K 0 0200400600 800100012001400160018002000 2,m
实验测量结果 0 200 400 600 800 1000 1200 1400 1600 1800 2000 0 2000 4000 6000 8000 10000 E(,T), mW/cm 2nm , nm 6000K 5500K 5000K 4000K 3000K

实验测量结果(以频率表示) 1.40E-008 6000K 1.20E-008 E 1.00E-008 8.00E-009 5000K 日 6.00E-009 4.00E-009 4000K 2.00E-009 3000K 0.00E+000 0.00E+000 5.00E+014 1.00E+015 1.50E+015 2.00E+015 v,Hz
实验测量结果(以频率表示) 0.00E+000 5.00E+014 1.00E+015 1.50E+015 2.00E+015 0.00E+000 2.00E-009 4.00E-009 6.00E-009 8.00E-009 1.00E-008 1.20E-008 1.40E-008 E(,T), mW/cm 2s , Hz 6000K 5000K 4000K 3000K

黑体辐射的定律 ·1、Stefan-Boltzmann定律(1879年、1884年) ·2、Wien位移定律(1893年) ·3、Rayleigh-Jeans定律(1900年,1905年) Stefan Wien Rayleigh Jeans
黑体辐射的定律 • 1、Stefan-Boltzmann定律(1879年、1884年) • 2 、 Wien位移定律(1893年) • 3 、Rayleigh-Jeans定律(1900年,1905年) Stefan Wien Rayleigh Jeans

1、Stefan-Boltzmann定律 辐射的总能量,即曲线下的面积与T成正比 10000 Φ(T)=E(y,T)dv=oT4 8000 5500 6000 o=5.67032×10-18W/m2K4 5000 4000 2000 4000K Stefan-Boltzmann常数 3000K 0200400600800100012001400160018002000 元,nm
1、Stefan-Boltzmann定律 辐射的总能量,即曲线下的面积与T 4成正比 4 0 ( ) ( , )d T E T T = = 18 2 4 5.67032 10 W/m K − = Stefan-Boltzmann常数 0 200 400 600 800 1000 1200 1400 1600 1800 2000 0 2000 4000 6000 8000 10000 E(,T), mW/cm 2nm , nm 6000K 5500K 5000K 4000K 3000K
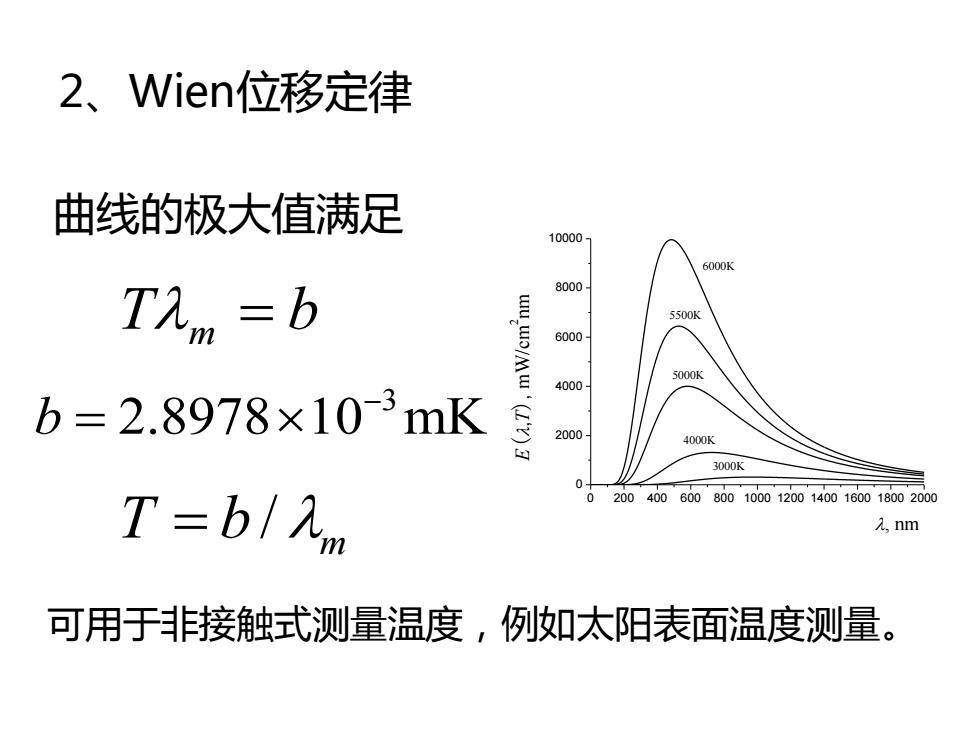
2、Wien位移定律 曲线的极大值满足 10000 6000K 8000 TAm =b 5500 6000 5000K 4000 b=2.8978×10-3mK (Iv)3 2000 4000K 3000K 0 T=b/九m 0200400600800100012001400160018002000 A,nm 可用于非接触式测量温度,例如太阳表面温度测量
2、Wien位移定律 曲线的极大值满足 T m = b / T b = m 可用于非接触式测量温度,例如太阳表面温度测量。 3 b 2.8978 10 mK − = 0 200 400 600 800 1000 1200 1400 1600 1800 2000 0 2000 4000 6000 8000 10000 E(,T), mW/cm 2nm , nm 6000K 5500K 5000K 4000K 3000K
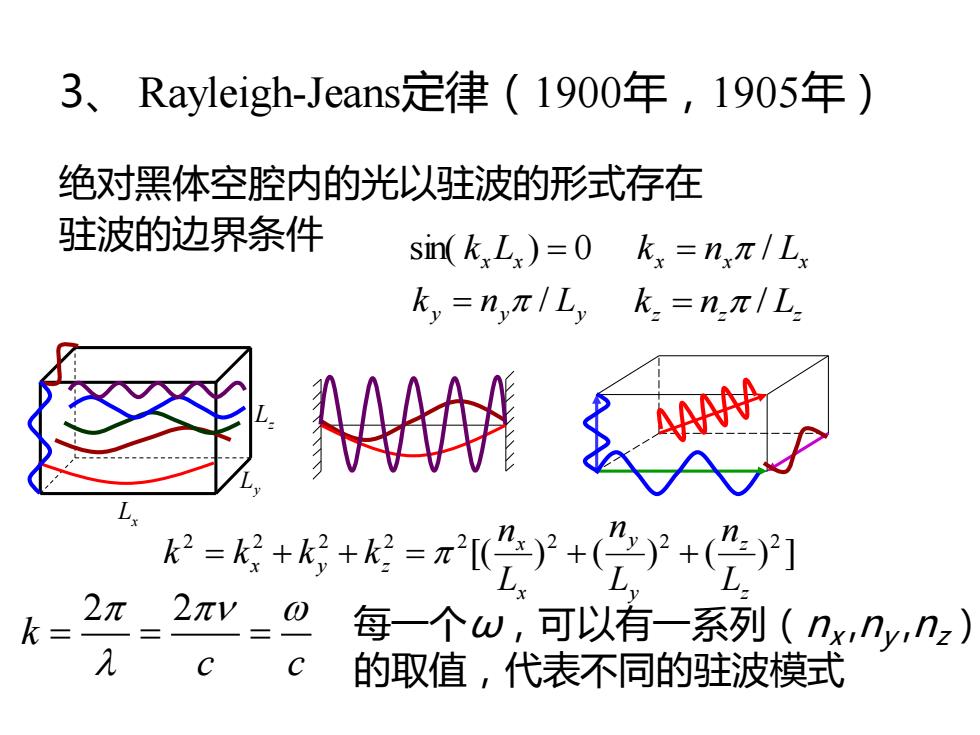
3、Rayleigh-Jeans7定律(1900年,1905年) 绝对黑体空腔内的光以驻波的形式存在 驻波的边界条件 sin(kLx)=0kx=nπ/L ky=nπ/Lyk.=nπ/L 4 =发++=++(门 k= 2π2π_0 每一个w,可以有一系列(nx,ny,nz) 的取值,代表不同的驻波模式
3、 Rayleigh-Jeans定律(1900年,1905年) 绝对黑体空腔内的光以驻波的形式存在 驻波的边界条件 sin( kx Lx ) = 0 x nx Lx k = / y ny Ly k = / z nz L z k = / [( ) ( ) ( ) ] 2 2 2 2 2 2 2 2 z z y y x x x y z L n L n L n k = k + k + k = + + L x L z L y 2 2 k c c = = = 每一个ω,可以有一系列(nx ,ny ,nz) 的取值,代表不同的驻波模式

单位体积内、频率在V~V4d的驻波数为 1 dn,=8π万dv odv=sv'd 1 而从小孔辐射出的驻波数为Tdv=cpd 4 每一个驻波的能量为kT 辐射出的能量,即辐射本领为 W E(v,T)dv=kTTdv= 2π 以波长表示为E(几,T)d元= 2πCkTd2
2 3 8 d d c = 单位体积内、频率在ν~ν+dν的驻波数为 2 3 d 8 d n c = 1 4 而从小孔辐射出的驻波数为 = d c d 2 2 2 E T kT kT ( , )d d d c = = 辐射出的能量,即辐射本领为 每一个驻波的能量为kT 4 2 ( , )d c E T kTd 以波长表示为 =