
2021/11/4 无机材料的热学性能 热学性能 ·本章讨论的无机材料的热学性能包括热容、热膨胀、热传 执 之性 熔化和升华禁, 微观本质关系加以探过, ·晶体点阵中的质点(原子、离子)总是围绕着平衡位置作微 对富格燕浪籍卖报动。材料的各种热性能的物理本质, ·如果设每个原子的质量为m,在任一瞬间该原子在x方向的 位移为x。其相邻原子的的位移为x1和x.其运动方程为 mX票=1十1-2) 1
2021/11/4 1 无机材料的热学性能 • 本章讨论的无机材料的热学性能包括热容、热膨胀、热传 导、热稳定性、熔化和升华等,针对热学性能和无机材料 的宏观、微观本质关系加以探讨,以便在选材、用材、改 善材质、探讨新材料、新工艺方面打下物理理论基础。 • 晶体点阵中的质点(原子、离子)总是围绕着平衡位置作微 小振动,称为晶格热振动。材料的各种热性能的物理本质, 均与晶格热振动有关。 • 如果设每个原子的质量为m,在任一瞬间该原子在x方向的 位移为xn 。其相邻原子的的位移为xn-1和xn+1,其运动方程为 热学性能

2021/11/4 热学性能 ·晶体中有N个原子,存在N个频率的振动。原子间有着很 蛋的提果动以在餐新玻密不 个原子的振动会使邻近与原子随之振 传播。品体的热能为热运动时能量的总和。 m数 =8=1.5×10(Hz) ·频率较低的格波,临近原子彼此之间的位相差不大,则格 波类似于弹性体中的应变波,称为“声频支振动”。频率 甚高的振动波,邻近原子的位相差很大,几乎相反时,频 率往往在红外光区,称为“光频支振动”。 热学性能 w关专安 图3.1一维双原子点阵中的格波 (a)声频支,()光额支。 ·若晶胞中包含了两种不同的原子,声频支可以看成是相邻 男活霜整同的振动方向,光频支的板动成相舒原子我动 ·若为离子型晶体,光频支的振动导致正、负离子间的相对 位移时,构成了 一个偶极子 ,在振动过程中偶极子的偶极 矩是周期性变化的,产生电磁波,反之相应颜率的红外光 可以被晶体强烈吸收。 2
2021/11/4 2 • 晶体中有N个原子,存在N个频率的振动。原子间有着很 强的相互作用力,一个原子的振动会使邻近与原子随之振 动,使晶格振动以弹性波的形式(又称格波)在整个材料内 传播。晶体的热能为热运动时能量的总和。 • 弹性波在固体中的传播速度约为3×103m/s,晶格常数a通 常在10-10m数量级,而声频振动的最小周期为2a,可以估 算最大的振动频率为 • 频率较低的格波,临近原子彼此之间的位相差不大,则格 波类似于弹性体中的应变波,称为“声频支振动”。频率 甚高的振动波,邻近原子的位相差很大,几乎相反时,频 率往往在红外光区,称为“光频支振动”。 热学性能 • 若晶胞中包含了两种不同的原子,声频支可以看成是相邻 原子具有相同的振动方向,光频支的振动成相邻原子振动 方向相反。 • 若为离子型晶体,光频支的振动导致正、负离子间的相对 位移时,构成了一个偶极子,在振动过程中偶极子的偶极 矩是周期性变化的,产生电磁波,反之相应频率的红外光, 可以被晶体强烈吸收。 热学性能

2021/11/4 无机材料的热容 ·热容是分子热运动的能量随温度而变化的一个物理量,其 定义为物体温度升高1K所需要增加的能量: C.-(/K) 二塞为题意质的务茶物 尔热容”,单位是/(K.mol)。 ·工程上的热容:物质从温度T,到T,所吸收的热量的平均值 比较粗略,温度范围越大,与实际热容相差越大 无机材料的热容 ·加热过程是恒压条件下进行的,所测定的热容称恒压热容 (C。)。假如加热过程保持物体容积不变,所测定的热容称 为恒容热容C,)。 道 其中H为焓,E为热能。 ·恒压加热过程中,物体除温度升高外还要对外界做功,所 以温度每提高1K要吸收更多的热量,即C,>C, ·可以导出9,-6,=T/B 积:云为件影张系数,一若为压缩系数。V,为摩尔容 ·凝聚态材料,低温下两者相差不大,高温下有显著的差异。 3
2021/11/4 3 • 热容是分子热运动的能量随温度而变化的一个物理量,其 定义为物体温度升高1K所需要增加的能量: • 一般定义为一定质量的物质的热容:一克物质的热容称为 “比热容”,单位是J/(K.g)或一摩尔物质的热容称为“摩 尔热容”,单位是J/(K.mol) 。 • 工程上的热容:物质从温度T1 到T2 所吸收的热量的平均值 比较粗略,温度范围越大,与实际热容相差越大 无机材料的热容 • 加热过程是恒压条件下进行的,所测定的热容称恒压热容 (Cp ) 。假如加热过程保持物体容积不变,所测定的热容称 为恒容热容(Cv )。 其中H为焓,E为热能。 • 恒压加热过程中,物体除温度升高外还要对外界做功,所 以温度每提高1K要吸收更多的热量,即Cp > Cv • 可以导出 为体膨胀系数, 为压缩系数。V0 为摩尔容 积。 • 凝聚态材料,低温下两者相差不大,高温下有显著的差异。 无机材料的热容

2021/11/4 晶态固体热容的经验定律和经典理论 ·杜降-珀替定律:桓压下元素晶体的原子热容为25/K.mo) ·柯普定律:化合物分子热容等于构成此化合物各元素原子 热容之和。 ·大部分元素的原子热容都接近该值,特别在高温时符合得 更好,但轻元素的晶体需要利用下面的值 元素HBc0FPSa C,1/K·mo19.611.37.516.720.915.922.522.520.4 ·杜隆一珀替定律在高温时与实验结果是很符合的。但在低 温时,热容的实验值并不是一个恒量。它随温度降低而减 小,在接近绝对零度时,热容值按T的规律趋于零。对于 低温下热容需要用量子理论来解释。 晶态固体热容的经验定律和经典理论 ·根据晶格振动理论,在固体中可以用谐振子代表每个原子 在一个自由度的振动,按照经典理论,能量按自由度均分 每一振动自由度的平均动能和平均位能都为12kT。总能 量为3kT。其总能量可表达为 E=3NKT =3RT ·热容可表达为 。-(2.-「2321-3t-3球 25d/·my ·根据柯普定律,对于双原子化合物,热容为2,三原子为 3R,以此类推
2021/11/4 4 • 杜隆-珀替定律;桓压下元素晶体的原子热容为25J/(K.mol)。 • 柯普定律:化合物分子热容等于构成此化合物各元素原子 热容之和。 • 大部分元素的原子热容都接近该值,特别在高温时符合得 更好,但轻元素的晶体需要利用下面的值 • 杜隆—珀替定律在高温时与实验结果是很符合的。但在低 温时.热容的实验值并不是一个恒量。它随温度降低而减 小,在接近绝对零度时,热容值按T3 的规律趋于零。对于 低温下热容需要用量子理论来解释。 晶态固体热容的经验定律和经典理论 • 根据晶格振动理论,在固体中可以用谐振子代表每个原子 在一个自由度的振动,按照经典理论,能量按自由度均分, 每一振动自由度的平均动能和平均位能都为1/2kT。总能 量为3kT。其总能量可表达为 • 热容可表达为 • 根据柯普定律,对于双原子化合物,热容为2R,三原子为 3R,以此类推 晶态固体热容的经验定律和经典理论

2021/11/4 晶态固体热容的量子理论回顾 ·普朗克在研究黑体辐射时,提出振子能量的量子化理论 其能量为nhv -0123 量子数) 其中h为普朗 克常数,v为频率。h6.626×1034.5。也可以写成=共= 按照统计热力学的原理,在温度T时,具有的能量为nhv能 量的振子的几率为 意/公岁 · ·多项式展开,化简后得到 晶态固体热容的量子理论回顾 ·当,亭,与经典理论一致。 ·在室温下,=4.14×10-,最大振动频率可估算为 6x×1013rad/s,则()=9.93X10-"」,7<w,因此只有当温 度较高时,可按经典理论计算热容。 瑞 -24-立” ·热容可表达为 。-.- 5
2021/11/4 5 • 普朗克在研究黑体辐射时,提出振子能量的量子化理论。 其能量为nh(n=0、1、2、3,量子数),其中h为普朗 克常数, 为频率。h=6.62610-34J.s。也可以写成 • 按照统计热力学的原理,在温度T时,具有的能量为nh能 量的振子的几率为 • 根据麦克斯威-波尔兹曼分配定律可推导出:在温度为T时, 一个振子的平均能量为 • 多项式展开,化简后得到 晶态固体热容的量子理论回顾 • 当 , ,与经典理论一致。 • 在室温下, ,最大振动频率可估算为 61013rad/s,则 J, ,因此只有当温 度较高时,可按经典理论计算热容。 • 由于1摩尔固体中有N个原子,每个原子的热振动自由度是 3。所以1摩尔固体的振动可看做3N个振子的合成振动,则 1摩尔固体的平均能量为 • 热容可表达为 • 精确计算需要知道振子频谱,十分困难。利用爱因斯坦模 型和德拜模型进行简化。 晶态固体热容的量子理论回顾 1 1 E kT kT

2021/11/4 晶态固体热容的量子理论回顾 ·爱因斯坦模型:每一个原子都是一个独立的振子,原子之 间彼此无关。并且都是以相同的角频率振动 1-头公二,变为=w× -開1.-到产变为。-是-m- ·为爱因斯坦比热函数,可通过选取适当的角频率, 获得理论c,与实际值的吻合。 ·爱因斯坦温度:,=0,当温度很高时,即T>0,利用下 面的关系式 -子-1+警++制”1+号 得到 c,=3Nk 晶态固体热容的量子理论回顾 ·根据爱因斯坦模型,高温下的热容符合杜隆珀替公式。 ·在低温时,即T<0E, 6一等m产可近似为=子 ·主要原因:各原子的振动不是彼此独立地以同样频率振动 ,原子振动间有耦合作用,温度低时这一效应尤其显著。 忽略振动之间频率的差别是此模型在低温不准的另一原因 、 6
2021/11/4 6 • 爱因斯坦模型:每一个原子都是一个独立的振子,原子之 间彼此无关.并且都是以相同的角频率振动。 变为 变为 • 为爱因斯坦比热函数,可通过选取适当的角频率, 获得 理论cv 与实际值的吻合。 • 爱因斯坦温度: ,当温度很高时,即T>>E ,利用下 面的关系式 得到 晶态固体热容的量子理论回顾 3 v c Nk • 根据爱因斯坦模型,高温下的热容符合杜隆-珀替公式。 • 在低温时,即T<< E , 可近似为 • 实验测量到的cv 随T3 变化,按爱因斯坦模型计算的热容比 实际热容随温度下降地更快。 • 主要原因:各原子的振动不是彼此独立地以同样频率振动 ,原子振动间有耦合作用,温度低时这一效应尤其显著。 忽略振动之间频率的差别是此模型在低温不准的另一原因 。 晶态固体热容的量子理论回顾
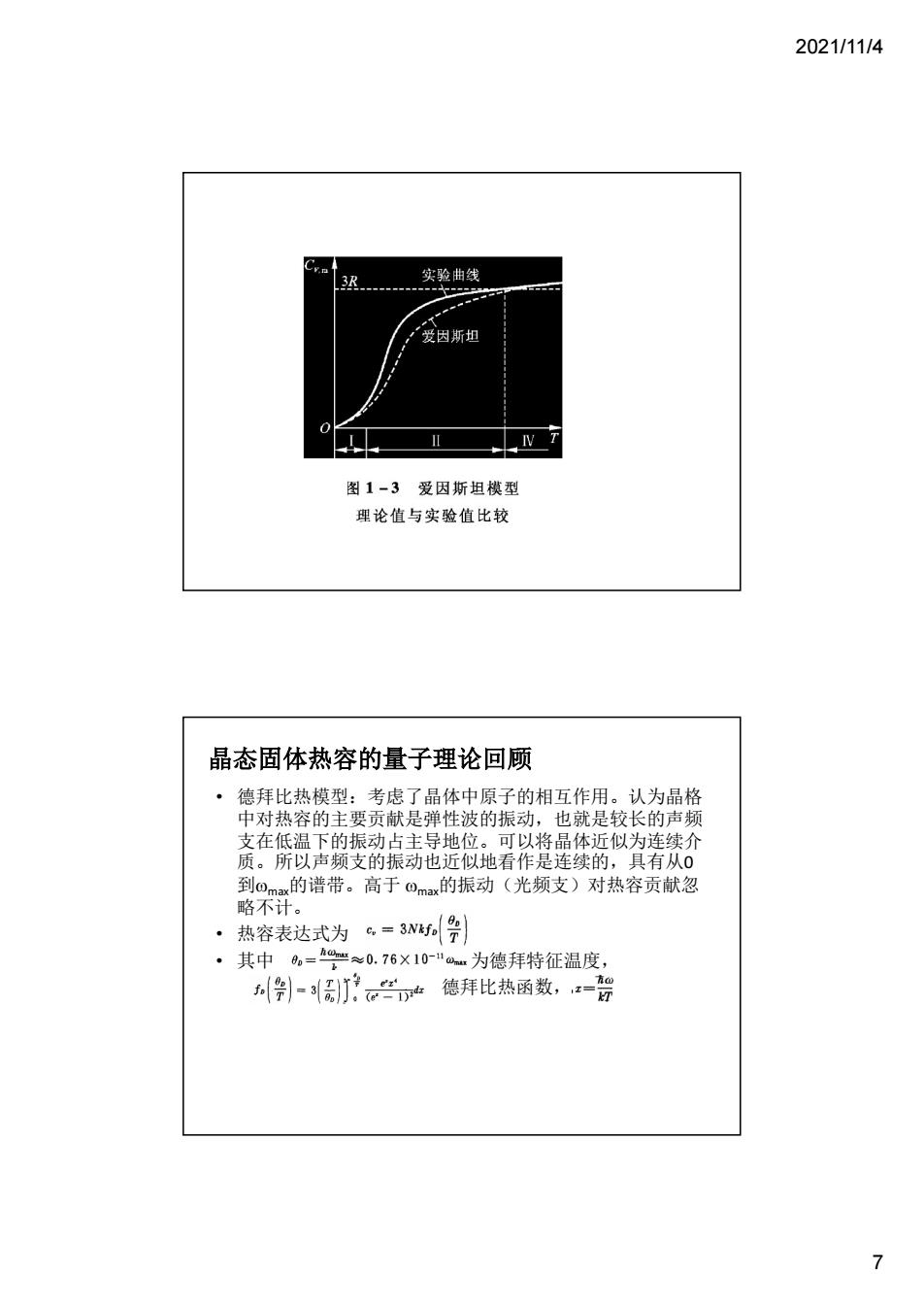
2021/11/4 实验曲线 爱因斯坦 图1-3爱因斯坦模型 理论值与实险值比较 晶态固体热容的量子理论回顾 ·热容表达式为6=3w。号 ·其中=≈0.76×10-"u为德拜特征温度 -引产德拜比热函数,-号 7
2021/11/4 7 • 德拜比热模型:考虑了晶体中原子的相互作用。认为晶格 中对热容的主要贡献是弹性波的振动,也就是较长的声频 支在低温下的振动占主导地位。可以将晶体近似为连续介 质。所以声频支的振动也近似地看作是连续的,具有从0 到max的谱带。高于 max的振动(光频支)对热容贡献忽 略不计。 • 热容表达式为 • 其中 为德拜特征温度, 德拜比热函数, 晶态固体热容的量子理论回顾

2021/11/4 晶态固体热容的量子理论回顾 ·当温度较高时,即T>0。,C,*3Nk即是杜降一珀替定律 ·当温度较低时,即T<0。 6-2g4别 但在很低的温度下,实验 ·远高于德拜温度,热容可以超过3R,需要考虑电子对热容 的贡献。 ·热容的量子理论,对于原子晶体和一部分较简单的离子晶 体,在较宽广的温度范围内都 与哈结里符 得很行 化合物。较复杂的分子结构住往会有 一各种高频旅动据合。多品、多相的无机材料,情况更为度 实验曲线 图1-4德拜模型理论值与实验值比较
2021/11/4 8 • 当温度较高时,即T>>D , 即是杜隆—珀替定律 • 当温度较低时,即T<<D • 在低温时,与实验符合的较好。但在很低的温度下,实验 测量的热容与温度成正比,偏离德拜模型。 • 远高于德拜温度,热容可以超过3R,需要考虑电子对热容 的贡献。 • 热容的量子理论,对于原子晶体和一部分较简单的离子晶 体,在较宽广的温度范围内都与实验结果符合得很好,但 并不完全适用于所有化合物。较复杂的分子结构往往会有 各种高频振动耦合。多晶、多相的无机材料,情况更为复 杂。 晶态固体热容的量子理论回顾 3 v c Nk

2021/11/4 无机材料的热容 ·根据德拜热容理论,在高于德拜温度 0。时,热容趋于常数25/K.mo,低 于0。时与T成正比。不同材料0是不 同的,取决于键的强度、材料的弹性 模量、熔点等,很多材料。约为熔点( 热力学温度)的0.2-0.5倍。 ·石墨0,为1973K,Be0为1173K,AN203 为923K等。 ·机材料的热容与材料结构的关系不大 热络09被基会精与ca50,的 ·相变时时存在着热容异常。 无机材料的热容 ·气孔的存在降低材料热容,因此一些多孔材料可以用来做 隔热耐火砖,吸收热量少,抗热震性好 ·盔公赛解骨度范围。材料热容与温度的关系可以用以下经 =++c-+ 其中c,的单位为4.18/川mol.K ·较高温度下固体的摩尔热容大约等于构成该化合物各元素 原子热容的总和 c-∑C n为元素的原子数,C为元素的摩尔热容 ·复合材料的热容可由以下公式计算 c-2ne g为元素的重量百分数,c为元素的比热容 9
2021/11/4 9 • 根据德拜热容理论,在高于德拜温度 D 时,热容趋于常数25 J/(K.mol),低 于D 时与T3 成正比。不同材料D 是不 同的,取决于键的强度、材料的弹性 模量、熔点等,很多材料D 约为熔点( 热力学温度)的0.2-0.5倍。 • 石墨D 为1973K,BeO为1173K,Al2O3 为923K等。 • 机材料的热容与材料结构的关系不大 ,CaO和SiO2 1:1的混合物与CaSiO3 的 热容-温度曲线基本重合。 • 相变时时存在着热容异常。 无机材料的热容 • 气孔的存在降低材料热容,因此一些多孔材料可以用来做 隔热耐火砖,吸收热量少,抗热震性好。 • 在一定的温度范围,材料热容与温度的关系可以用以下经 验公式计算 其中cp 的单位为4.18 J/(mol.K) • 较高温度下固体的摩尔热容大约等于构成该化合物各元素 原子热容的总和 ni 为元素i的原子数,Ci 为元素i的摩尔热容 • 复合材料的热容可由以下公式计算 gi 为元素i的重量百分数,ci 为元素i的比热容 无机材料的热容

2021/11/4 无机材料的热膨胀 ·密物体的体积或长度随温度的升高而增大的联象称为 ·假设物体原来的长度为。温度升高△t后长度的增加量为△ ·4为线膨胀系数,即材料升高升高1K时的伸长,此时的长 度为 L=+三(1+a,) 品品金药品高酒温变升高清加大。无机材膨张 ·体膨胀系数α,:物体体积随温度的增长可表示为 =(1+ama) 对于各向同性的材料,≈3a 各向异性的材料 w=+a十a 其中a,a。,a分别为三个晶向的膨胀系数 无机材料的热膨胀 卓触聚系整空聚累费内的 NO. ”。-高,a=爵 程影琴泰数在无机材料中是个重要的 国1,五其落无航针制的移腰塞系数与第青的关 之起的热相无材复合中各相及名方】 吸度不高,相在商温时内方清能,安易因 一般热膨胀系数小的材料热稳定高,比如S1N4 10
2021/11/4 10 • 定义:物体的体积或长度随温度的升高而增大的现象称为 热膨胀。 • 假设物体原来的长度为l。温度升高t后长度的增加量为l • l 为线膨胀系数,即材料升高升高1K时的伸长,此时的长 度为 • l 不是一个常数,通常随温度升高而加大。无机材料膨胀 系数的量级约10-5-10-6/K。 • 体膨胀系数v :物体体积随温度的增长可表示为 • 对于各向同性的材料, 各向异性的材料 其中a , b ,c 分别为三个晶向的膨胀系数 无机材料的热膨胀 • 上述的膨胀系数为特定温度范围内的 平均值,某一温度膨胀系数为 • 一般隔热用耐火材料的膨胀系数是 200-1000oC的平均值。 • 热膨胀系数在无机材料中是个重要的 性能参数: 无机材料的热膨胀 – 玻璃陶瓷与金属之间的封接工艺,由于电真空的要求,需要在低温 和高温下两种材料的l 值相近。比如高温钠蒸灯所用的透明Al2O3 灯 管, l=810-6,封装金属铌l=7.810-6 。 – 在多晶、多相无机材料以及复合材料中,各相及各方向的l 不同所 引起的热应力问题已成为选材、用材的突出矛盾。例如石墨垂直于 c轴方向的l=110-6 ,平行于c轴方向的l=2710-6 ,常温下极易因 热应力较大而强度不高,但在高温时内应力消除,强度反而升高。 • 一般热膨胀系数小的材料热稳定高,比如Si3N4