
2021/10/11 无机材料的阻尼性能(内耗) 材料物理性能,田莳编著 材料的阻尼性能(内耗) ·振动的固体,即使与外界完全隔绝,真空环境下会逐渐静 止下来。如我们用一个铜丝吊一个圆盘使其扭动,最终会 停止下来。如果是强迫振动,则外界必须不断供给固体能 量,才能维持振动。 ·能量耗散来源于材料内部。 ·机械振动能量由于内部的某种物理过程而引起的能量耗损 称为内耗。对于高频振动(兆赫兹以上), 这种能量损耗 又称超声衰减。在工程领域又称内耗为阻尼 ·典型实例: 一寺院 大钟 一人的脊椎 7
2021/10/11 1 无机材料的阻尼性能(内耗) 材料物理性能,田莳编著 • 振动的固体,即使与外界完全隔绝,真空环境下会逐渐静 止下来。如我们用一个铜丝吊一个圆盘使其扭动,最终会 停止下来。如果是强迫振动,则外界必须不断供给固体能 量,才能维持振动。 • 能量耗散来源于材料内部。 • 机械振动能量由于内部的某种物理过程而引起的能量耗损 称为内耗。对于高频振动(兆赫兹以上),这种能量损耗 又称超声衰减。在工程领域又称内耗为阻尼。 • 典型实例: – 寺院中的大钟 – 人的脊椎骨 材料的阻尼性能(内耗)

2021/10/11 材料的阻尼性能(内耗) ·内耗在20世纪40年代开始成为一门独立的学科。它已从专 门研究金属品体材料为对象扩展到高分子、非品态和复合 材料:研究内容从材料内部结构一直到薄膜、表面,甚至 青蛙腿部肌肉疲劳内耗,为解决材料科学和工程课题做出 了贡献。 ·研究内容。 一内耗学科的基础研究 批致这究所用力个体性品不会产生性变形 材料的阻尼性能(内耗) ·引起振动能量耗散的根本原因是固体材料在应力的作用下 出现了非弹性应变(完全弹性体时不产生内耗的) ·理想的弹性体,应力应变间满足三个条件: 一单值性:应力应变一一对应,对应一个应力总有一个确定的应变。 一瞬时性:响应不需要时间,瞬间完成。 一线性:应力与应变成正比关系。 不同类型的固体的区别 夏珠性事撑族券带殊性体粘养性体壳金赛剂 单值性 2
2021/10/11 2 • 内耗在20世纪40年代开始成为一门独立的学科。它已从专 门研究金属晶体材料为对象扩展到高分子、非晶态和复合 材料;研究内容从材料内部结构一直到薄膜、表面,甚至 青蛙腿部肌肉疲劳内耗,为解决材料科学和工程课题做出 了贡献。 • 研究内容: – 内耗学科的基础研究。 – 内耗对固体中缺陷的运动及结构的变化敏感,内耗用于固体研究 缺陷及其相互作用的研究,研究材料中各种缺陷的弛豫及产生相 变的机制。这种研究所用应力极小,对样品不会产生塑性变形, 干扰比较小。缺陷:点、线、面、体缺陷。 – 寻求适合工程应用的有特殊阻尼本领的材料(通常用在两个极端。 内耗极小的材料,如制备钟表游丝,晶场显微镜的探针材料;内 耗很大的材料,如隔音材料,潜艇的螺旋桨及风机)。 材料的阻尼性能(内耗) • 引起振动能量耗散的根本原因是固体材料在应力的作用下 出现了非弹性应变(完全弹性体时不产生内耗的) • 理想的弹性体,应力应变间满足三个条件: – 单值性:应力-应变一一对应,对应一个应力总有一个确定的应变。 – 瞬时性: 响应不需要时间,瞬间完成。 – 线性:应力与应变成正比关系。 材料的阻尼性能(内耗) 理想弹性 体 非线性弹 性体 滞弹性体 粘弹性体 完全非弹 性体 单值性 √ √ √ 瞬时性 √ √ 线 性 √ √ √ 不同类型的固体的区别
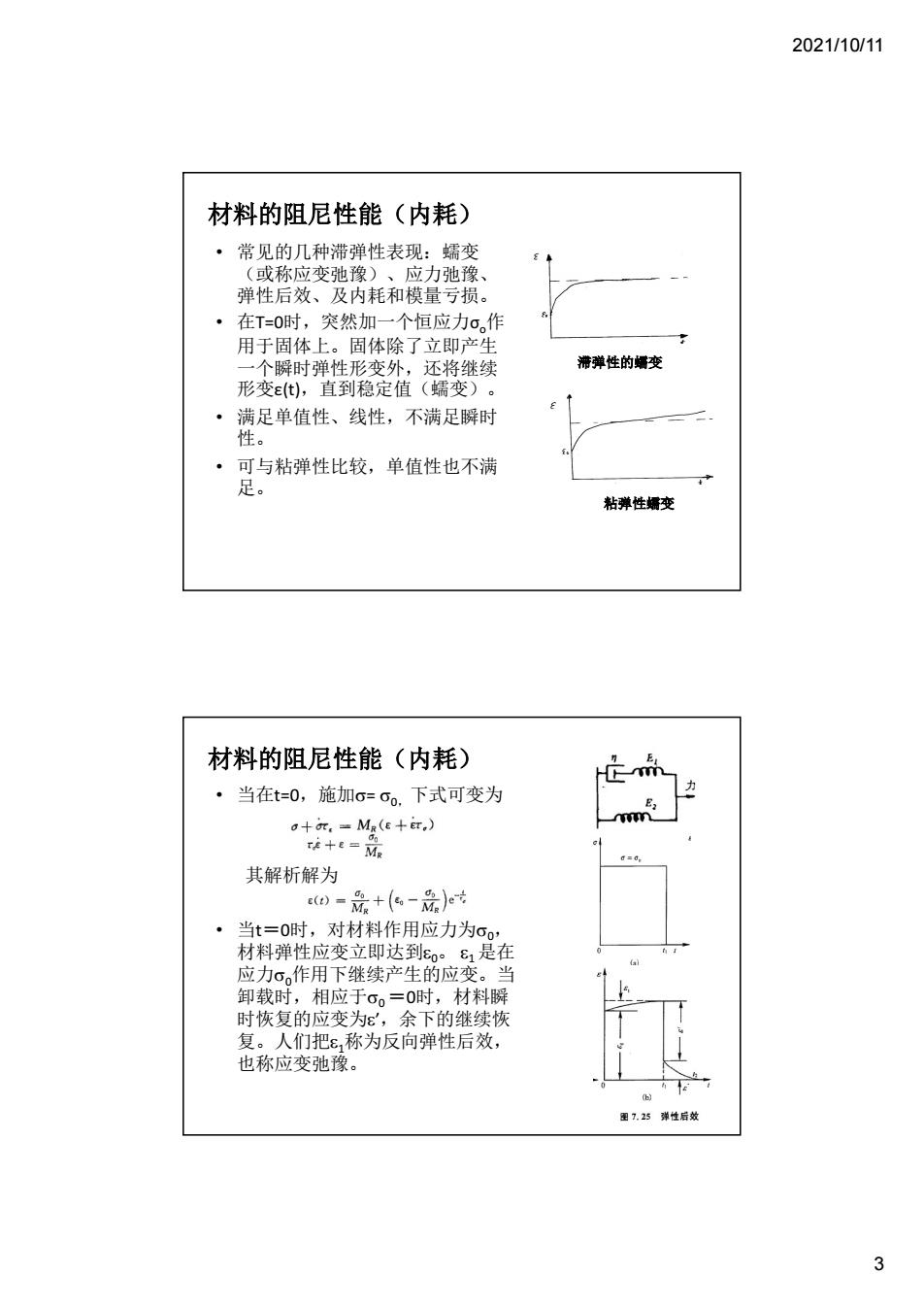
2021/10/11 材料的阻尼性能(内耗) ·在T=0时,突然加一个恒应力σ。作 用于固体上。固体除了立即产生 ,个瞬时弹性形变外,还将继续 滞弹性的变 形变ε,直到稳定值(蠕变)。 使足单值能、性,不清定对时 ·可与粘弹性比较,单值性也不满 足。 粘弹性婚变 材料的阻尼性能(内耗) ·当在t=0,施加o=co.下式可变为 装+ 其解析解为 0=是+(6-是)) 当t=0时,对材料作用应力为og 材料弹性应变立即达到:是在 应力σ作用下继续产生的应变。当 卸载时,相应于σo=0时,材料瞬 时恢复的应变为ε',余下的继续恢 复。人们把ε称为反向弹性后效, 也称应变弛豫。 性后效 3
2021/10/11 3 • 常见的几种滞弹性表现:蠕变 (或称应变弛豫)、应力弛豫、 弹性后效、及内耗和模量亏损。 • 在T=0时,突然加一个恒应力σo 作 用于固体上。固体除了立即产生 一个瞬时弹性形变外,还将继续 形变ε(t),直到稳定值(蠕变)。 • 满足单值性、线性,不满足瞬时 性。 • 可与粘弹性比较,单值性也不满 足。 材料的阻尼性能(内耗) 滞弹性的蠕变 粘弹性蠕变 • 当在t=0,施加= 0,下式可变为 其解析解为 • 当t=0时,对材料作用应力为0 , 材料弹性应变立即达到0 。 1 是在 应力0 作用下继续产生的应变。当 卸载时,相应于0 =0时,材料瞬 时恢复的应变为’,余下的继续恢 复。人们把1 称为反向弹性后效, 也称应变弛豫。 材料的阻尼性能(内耗)

2021/10/11 材料的阻尼性能(内耗) ·当在t=0,8=8o.下式可变为 a+i.-Ma(c+ir.) ra +a-Mxco ·其解析解为 围7.27恒应变下的应力地津 (0)Mut,+(a.-Mao)ev ·应力需要一段时间达到稳定值, 应力弛豫 材料的阻尼性能(内耗) ·单向快速加、卸载时,应变弛豫来不及 产生,此时弹性模量可表达为 E=M=2 ·单向缓慢加、卸载,应变来得及充分进 行,此时弹性模量为 E=M■+6石 此时称M为完全弛豫性模量 ·在实际测量中,加载速度在上述两者之 间,测得弹性模量也在M,和Ma之间。 此时的弹性模量称为动态弹性模量。为 了表征材料因滞弹性而引起的弹性模量 下降,引入模量亏损或AE效应参量 “=' 4
2021/10/11 4 • 当在t=0,= 0,下式可变为 • 其解析解为 • 应力需要一段时间达到稳定值, 应力弛豫 材料的阻尼性能(内耗) • 单向快速加、卸载时,应变弛豫来不及 产生,此时弹性模量可表达为 • 单向缓慢加、卸载,应变来得及充分进 行,此时弹性模量为 此时称MR 为完全弛豫性模量 • 在实际测量中,加载速度在上述两者之 间,测得弹性模量也在Mu 和MR 之间。 此时的弹性模量称为动态弹性模量。为 了表征材料因滞弹性而引起的弹性模量 下降,引入模量亏损或E效应参量 材料的阻尼性能(内耗)

2021/10/11 材料的阻尼性能(内耗) 阳个本并 w-。公- ·在交变应力作用下,由于应变的非瞬时响应将引起应变落后 于应力,那么应变对应力的响应就会出现应力应变回线。 高剂巴选变两程大水为一个应力周别内能量的损托因此 ·对于理想弹性体,应力应变成直线,无回滞面积,无损耗 内耗的表征 图 ·利用上面回滞曲线内包围的面积△W表示内耗。 ·一般将内耗定义为Q1=1/2m(aw/W) 其中W为储存的弹性能 ·其中AW aWfodetsin atd sin(ae-p)xsinp W可表达为w- 。所以Q-W-ain gr tan pr?(当角很小时) 5
2021/10/11 5 • 在交变应力作用下,由于应变的非瞬时响应将引起应变落后 于应力,那么应变对应力的响应就会出现应力-应变回线。 • 应力回线的面积大小为一个应力周期内能量的损耗,因此, 可用它定义内耗。 • 对于理想弹性体,应力-应变成直线,无回滞面积,无损耗 。 材料的阻尼性能(内耗) • 利用上面回滞曲线内包围的面积ΔW表示内耗。 • 一般将内耗定义为Q-1=1/2π(ΔW/W) 其中W为储存的弹性能 • 其中W W可表达为 • 所以 内耗的表征

2021/10/11 内耗的表征 ”假说子应变落后一个相组。则应变可表达为 (cos-isin)eut=(E-i) ·弹性模量可表达为E=E+iE2 ·tg中=E,/E1.与上述推导的Q1等价。 用的方法有两类。共振系统的实验(包括强迫振动、自由 衰减、磁共振)和波传播法。 几种常见的内耗类型 ·由材料滞弹性行为引起的内耗,即其内耗源于应变落后于 应力引起的非弹性,属于弛豫型内耗。 弛豫型内耗可用Zener提出的应力、应变方程(线性微分 方程)表述。其通式为 apo+ada/dt+a d2o/dt2+.=bo+b dE/dt +b2 d2E/dt2+. 两边各取一项a0=b。E,即o=Me,胡克定律 两边各取两项,即只考虑一阶线性微分方程 aota,d'=b+b.' 与前面推导的关系式一致 a+ir,-Ma(e+ir,) ·存在着下述关系÷=臣(M,=o/为前述的未弛豫 模量,又称完全弹性模量) 6
2021/10/11 6 • 假设σ =σo e iωt,应变落后一个相角,则应变可表达为 = εo e i(ωt-φ) =εo (cosφ –isinφ) e iωt = (ε1 -iε2 ) e iωt • 弹性模量可表达为E=E1 +iE2 • tgφ=E2 /E1,与上述推导的Q-1等价。 • Q-1 =1/2πΔW/W=tgφ =φ,φ是应变落后于应力的位相。 对晶体来说,φ一般是小量,因此直接精确测量φ是很困 难的,但我们可以通过其它物理量的测量来获得φ,通常 用的方法有两类。共振系统的实验(包括强迫振动、自由 衰减、磁共振)和波传播法。 内耗的表征 • 弛豫型内耗:不引起塑性形变的条件下(一般ε< 10-4 ) ,内耗与所加的外应力大小无关;而频率有关。 • 由材料滞弹性行为引起的内耗,即其内耗源于应变落后于 应力引起的非弹性,属于弛豫型内耗。 • 弛豫型内耗可用Zener提出的应力、应变方程(线性微分 方程)表述。其通式为 a0σ+a1dσ/dt+a3d 2σ/dt2 +.=b0 ε + b1 dε/dt +b2 d 2 ε/dt2 +. 两边各取一项 a0σ =b0 ε ,即 σ=M ε,胡克定律 两边各取两项,即只考虑一阶线性微分方程 a0σ+a1σ’=b0 ε + b1 ’ • 与前面推导的关系式一致 • 存在着下述关系 (Mu =σ0 / ε0 为前述的未弛豫 模量,又称完全弹性模量) 几种常见的内耗类型

2021/10/11 几种常见的内耗类型 ·根据下式a+x,-M(e+r) ·如果如固体承受的是周期性变化的力,0=0,e,则 E=e。etl,代入上式,得到 (1+iwr,)a=Mg(1+ior,)e ·其复模量可表达为 风==M+-总e+w[+平受】 ·对比应=M1+g),可以得到 ·T阳,MR=MM 得到Q1=tgφ=[M,-M/Mwr/1+w2r2)=△wr/1+w2r) 其中AM=(M,一M/M称为弛豫强度 几种常见的内耗类型 ·同样根据实部可以计算出模量亏损为 △M/M=Au/l1+w2t3 测量周期, 模量和内耗与@r的关系 ,故△M/M AM/M=A 7
2021/10/11 7 • 根据下式 • 如果如固体承受的是周期性变化的力,σ=σo e iωt,则 ε=εo e i(ωt-φ),代入上式,得到 • 其复模量可表达为 • 对比 ,可以得到 • 令τ= (τσ τε )1/2 , M= (MuMR )1/2 及利用τσ /τε =Mu /MR 得到Q-1=tgφ=[(Mu -MR )/M] ωτ/(1+ω2 τ2 ) = ΔM ωτ/(1+ω2 τ2 ) 其中ΔM = (Mu -MR )/M 称为弛豫强度。 几种常见的内耗类型 M M itg (1 ) • 同样根据实部可以计算出模量亏损为 ΔM/M =ΔM /(1+ω2 τ2 ) • Q-1与振幅无关,而与频率有关,内耗对 ln(ωτ)频率作图,可得在ωτ=1时,内耗最 大(Q-1=ΔM/2)。 • τ是弛豫时间,ω是外加频率,1/ω=T是 测量周期, 几种常见的内耗类型 模量和内耗与的关系 • ωτ=1,即 T=τ , 外加应力周期与滞弹性材料的弛豫时间吻合, 此时耗能最大。 • ωτ »1, τ »1/ω=T, 弛豫时间相对测量周期很慢,即振动一周内体 系来不及弛豫,试样行为接近完全弹性行为, Q-1很小;M→Mu , 故 ΔM/M →0; • ωτ« 1, τ« 1/ω=T, 弛豫时间远小于测量振动周期,弛豫很快完成 ,故每一瞬间应变都接近平衡值,因此Q-1很小;M→MR , ΔM/M=ΔM

2021/10/11 几种常见的内耗类型 ·若体系发生的弛豫过程是通过原子扩散来进行的,则弛豫 时间r和温度T的关系满足Arrhenius方程r=o eH/KT,其中H 为激活能。 利用wr=1,t=1w,可以得到w=oe,即Inw=n H/kTm .W=W1,T=Tm1,Inw =Inwo-H/KTm,w=W2,T=Tm2,Inw2= Inu。-H/kT 两式相减后,得到in(u1/w2)=-H/k1Tm ,以计算出激活能H。 ·或者测量得到不同测量频率下的Tm,画lnw~lT曲线,拟 合直线获得斜率,计算出H。 ·利用t=oe,可将内耗表示成温度的函数 Qr1=△wtpeH/k/1+w2t,2e2HkT) 几种常见的内耗类型 ·滞弹性材料中滞后回线的出现是实验的 动态性质的结果。如果实验中应力的增 加及去除都很慢,则不会出现内耗。因 此,这种滞后称为动态滞后。 静态滞后内耗的产生是由于应力和应变 加载 同 的变位 ·应力变化时,应变总是瞬时调整到相应 的值,因此这种滞后回线的面积是恒定 值,与振动频率无关,故称为静态滞后 内耗。 8
2021/10/11 8 • 若体系发生的弛豫过程是通过原子扩散来进行的,则弛豫 时间τ和温度T的关系满足Arrhenius方程τ =τ0 eH/kT,其中H 为激活能。 • 利用ωτ=1, τ=1/ω,可以得到ω =ω0 e -H/kT,即lnω =lnω0 - H/kTm • ω =ω1 , T=Tm1, lnω1 =lnω0 -H/kTm1, ω =ω2 , T=Tm2, lnω2 = lnω0 -H/kTm2,两式相减后,得到ln(ω1 / ω2 ) =-H/k(1/Tm1- 1/Tm2),可以计算出激活能H。 • 或者测量得到不同测量频率下的Tm,画lnω1/T曲线,拟 合直线获得斜率,计算出H。 • 利用τ =τ0 eH/kT, 可将内耗表示成温度的函数 Q-1= ΔMωτ0 eH/kT/(1+ω2 τ0 2 e2H/kT) 几种常见的内耗类型 • 滞弹性材料中滞后回线的出现是实验的 动态性质的结果。如果实验中应力的增 加及去除都很慢,则不会出现内耗。因 此,这种滞后称为动态滞后。 • 静态滞后内耗的产生是由于应力和应变 间存在多值函数关系,在加载时,同一 载荷下具有不同的应变值,完全去掉载 荷后有永久形变产生。仅当反向加载时 才能回复到零应变。 • 应力变化时,应变总是瞬时调整到相应 的值,因此这种滞后回线的面积是恒定 值,与振动频率无关,故称为静态滞后 内耗。 几种常见的内耗类型

2021/10/11 几种常见的内耗类型 ·引起静滞后的各种机制没有相似的应力:应变方程,所以 数学处理没有弛豫型内耗那样明确。 ·可针对具体机制进行计算,求出回线面积△w,再由公式 :Q-W ·静态滞后回线不是线性关系,因而内耗与振幅有关。与频 率无关是静滞后型内耗的特性。 几种常见的内耗类型 方程为, Me10+TMg0'+wo2Mg0"=E+TE'+wo2E" w,是共振系统的固有频率 ·将o=0,e,E=E,e代入上方程,M=/e=1- w2/w2)+iwt]/[(Mg1+w2Mg/w2)+iwtMg] ·由实部、虚部可求出模量亏损和内耗 Qr1=tgφ=△Mwr/I1-w2/w,2P+w2r2] △MWM=△MI(1-w2/w,2/(1-w2/w,22+w2r2) 9
2021/10/11 9 • 引起静滞后的各种机制没有相似的应力-应变方程,所以 数学处理没有弛豫型内耗那样明确。 • 可针对具体机制进行计算,求出回线面积W,再由公式 • 静态滞后回线不是线性关系,因而内耗与振幅有关。与频 率无关是静滞后型内耗的特性。 几种常见的内耗类型 • 阻尼型内耗:当试样的质量(相对惯性元M)不可忽 视,系统仍属于滞弹性范畴时,描述它的方程为, MR -1σ+τMR -1σ’+ ω0 -2MR -1σ’’ = ε +τε’+ω0 -2ε’’ ω0 是共振系统的固有频率 • 将σ=σo e iωt ,ε=εo e i(ωt-φ) 代入上方程, =σ/ε =[(1- ω2 /ω0 2 )+iωτ]/[( MR -1+ω2MR -1/ω0 2 )+iωτMR -1] • 由实部、虚部可求出模量亏损和内耗 Q-1=tgφ=ΔMωτ/[(1- ω2 /ω0 2 )2 +ω2 τ2 )] ΔM/M =ΔM [(1- ω2 /ω0 2 )/[( (1- ω2 /ω0 2 )2 +ω2 τ2 ) 几种常见的内耗类型 M

2021/10/11 几种常见的内耗类型 ·w,1》t (即很小,w小) 的共振行为 在w=心o时, 收形成内耗 ·w01《T,w2/w2→0 Q1=△wwt/1+w2r2) 形式上看与弛豫型内耗相同 ·前面德拜弛豫型内耗与T关系密切,T略 有改变,内耗峰对应的ω将有很大改变: 而共振型内耗与温度依赖性相对来说要 小得多,内耗峰对应的频率与温度不敏 感,w=k/m2 德拜弛豫 ,峰温随ω增加移向高温阻尼 共振型,峰温随增加有可能移向低温。 内耗产生机理 ·点阵中原子有序排列引起内耗:溶解在 固溶体中弧立的间隙原子、替代原子。 这些原子在固溶体中的无规律分布称为 无序状态。如果外加应力时,这些原子 所处位置的能量即出现差异,因而原子 要发生重新分布,即产生有序排列。这 种由于应力引起的原子偏离无规则状态 分布叫应力感生有序。 ·a-fe:体心立方结构,碳原子通常处在晶胞的棱边上或面 心处,即(1/2,0,0小、(0,1/2,0)或(0,0,1/2)和(1/2,1/2,0)位 置。如果沿Z方向加一拉伸应力,则弹性应力将引起晶胞 的畸变。这时晶胞不再是理想立方体,沿Z方向原子间距 拉长,而沿X、Y方向原子间距缩小。间隙原子将由(1/2,0, 0)位置跳跃到(0,0,1/2)位置上,因为间隙原子跳到这一位 置将降低晶体的弹性变形能。使得原子沿拉力方向分布。 10
2021/10/11 10 • ω0 -1 » τ (即τ很小,τω小) Q-1分母中ω2 τ2 所占的比重小,得到典型 的共振行为,在ω=ω0 时,发生共振吸 收形成内耗峰。 • ω0 -1 « τ ,ω2 /ω0 2→0 Q-1≈ ΔM ωτ/(1+ω2 τ2 ) 形式上看与弛豫型内耗相同 • 前面德拜弛豫型内耗τ与T关系密切,T略 有改变,内耗峰对应的ω将有很大改变; 而共振型内耗与温度依赖性相对来说要 小得多,内耗峰对应的频率与温度不敏 感,ω0 =(k/m)1/2 。 • 德拜弛豫型, 峰温随ω增加移向高温;阻尼 共振型, 峰温随ω增加有可能移向低温。 几种常见的内耗类型 阻尼共振型内耗的共振吸收峰 • 点阵中原子有序排列引起内耗:溶解在 固溶体中弧立的间隙原子、替代原子。 这些原子在固溶体中的无规律分布称为 无序状态。如果外加应力时,这些原子 所处位置的能量即出现差异,因而原子 要发生重新分布,即产生有序排列。这 种由于应力引起的原子偏离无规则状态 分布叫应力感生有序。 内耗产生机理 • -Fe:体心立方结构,碳原子通常处在晶胞的棱边上或面 心处,即(1/2, 0, 0)、(0, 1/2, 0)或(0, 0, 1/2)和(1/2, 1/2,0)位 置。如果沿Z方向加一拉伸应力,则弹性应力将引起晶胞 的畸变。这时晶胞不再是理想立方体,沿Z方向原子间距 拉长,而沿X、Y方向原子间距缩小。间隙原子将由(1/2, 0, 0)位置跳跃到(0, 0, 1/2)位置上,因为间隙原子跳到这一位 置将降低晶体的弹性变形能。使得原子沿拉力方向分布