
4.4夫琅禾费圆孔衍射 夫琅禾费圆孔衍射 望远镜的分辨本领:瑞利判据
4.4 夫琅禾费圆孔衍射 夫琅禾费圆孔衍射 望远镜的分辨本领:瑞利判据
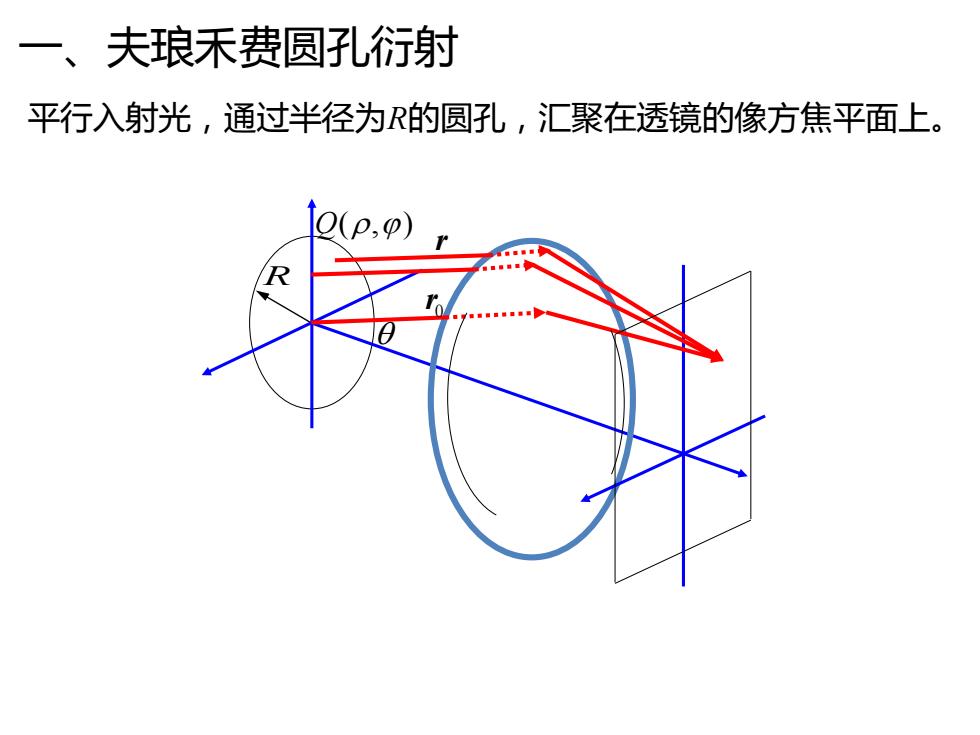
一、夫琅禾费圆孔衍射 平行入射光,通过半径为的圆孔,汇聚在透镜的像方焦平面上。 O(p,) R
一、夫琅禾费圆孔衍射 平行入射光,通过半径为R的圆孔,汇聚在透镜的像方焦平面上。 r 0 r Q(,) R
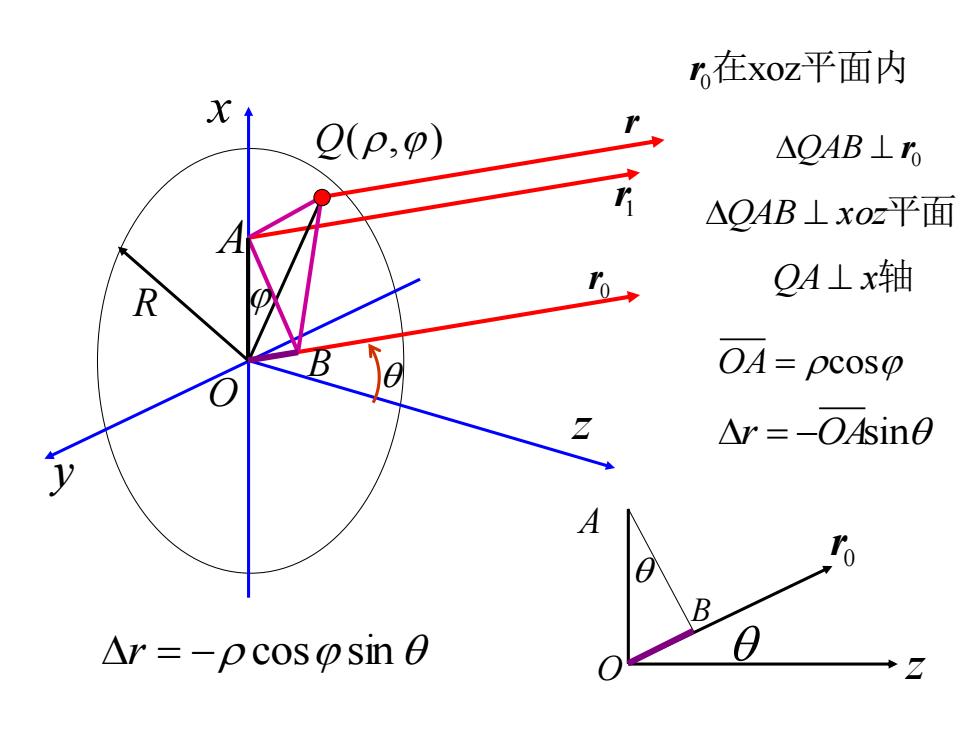
6在xoz平面内 Q(p,p) △QAB⊥ △OAB⊥xOz平面 QA⊥x轴 R 04=pcosp 2 Λr=-Osin0 A B △r=-o cososin 0 0 ◆ Z
r 0 r Q(,) r = − cos sin z R O A B x y 1 r ⊥ QAB 0 r 0 r 在xoz平面内 QA x ⊥ 轴 OA = cos = − r OAsin z 0 r O A B QAB ⊥ xoz平面

圆孔衍射的积分计算 Q(p,0)r )-K.00 d∑ 中o侧s Yo 令m=2πRsin0/=kRsin0 (P.cos(m 0)=K.2/(m) J,(m):一阶贝塞尔函数 ro m m
圆孔衍射的积分计算 y r 0 r Q(,) z R O x 0 cos sin 0 0 e ( ) ( , ) ( , ) d ikr ik U P K U F r − = 0 cos sin 0 0 e (0,0) e d d ikr ik KU r − = 0 2 0 0 0 0 e 2 (0,0) d cos( cos sin )d ikr R KU r = 令m R kR = = 2 sin / sin 0 2 0 0 0 0 e ( ) (0,0) d cos( cos )d ikr R U P KU m r R = 0 2 1 0 0 e 2 ( ) ( ) (0,0) ikr J m U KU R r m = J1(m):一阶贝塞尔函数 = + − = 0 2 ! 1 ) 2 ( ( 1)! ! 2 ( ) ( 1) k k k m m k k J m ] } 3! ) 2 ( [ 4 1 ] 2! ) 2 ( [ 3 1 ) 2 ( 2 1 {1 2 2 4 2 3 = − 2 + − + m m m m
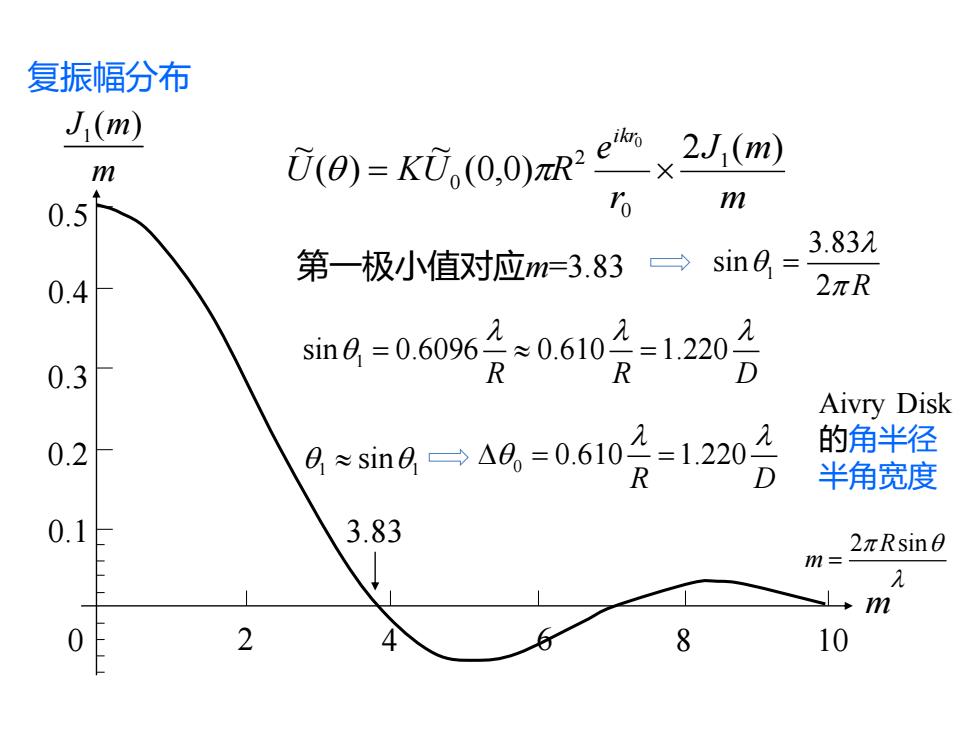
复振幅分布 J1(m) 2J1(m) m (0)=KU,(0.0 0.5 m 3.832 第一极小值对应m=3.83→sin8= 0.4 2πR sm8=-0606合s0610是120分 R R Aivry Disk 2 且*sin848,=0.610月=1220 的角半径 R 半角宽度 3.83 2πRsin0 m= 2 4 8 10
复振幅分布 m J m r e U KU R ikr 2 ( ) (0,0) ~ ( ) ~ 1 0 2 0 0 = 0 2 4 6 8 10 1 J m( ) m m 0.1 0.2 0.3 0.4 0.5 2 sin R m = 3.83 1 3.83 sin 2 R = 1 sin 0.6096 0.610 1.220 R R D = = 0 0.610 1.220 R D = = Aivry Disk 的角半径 半角宽度 第一极小值对应m=3.83 1 1 sin
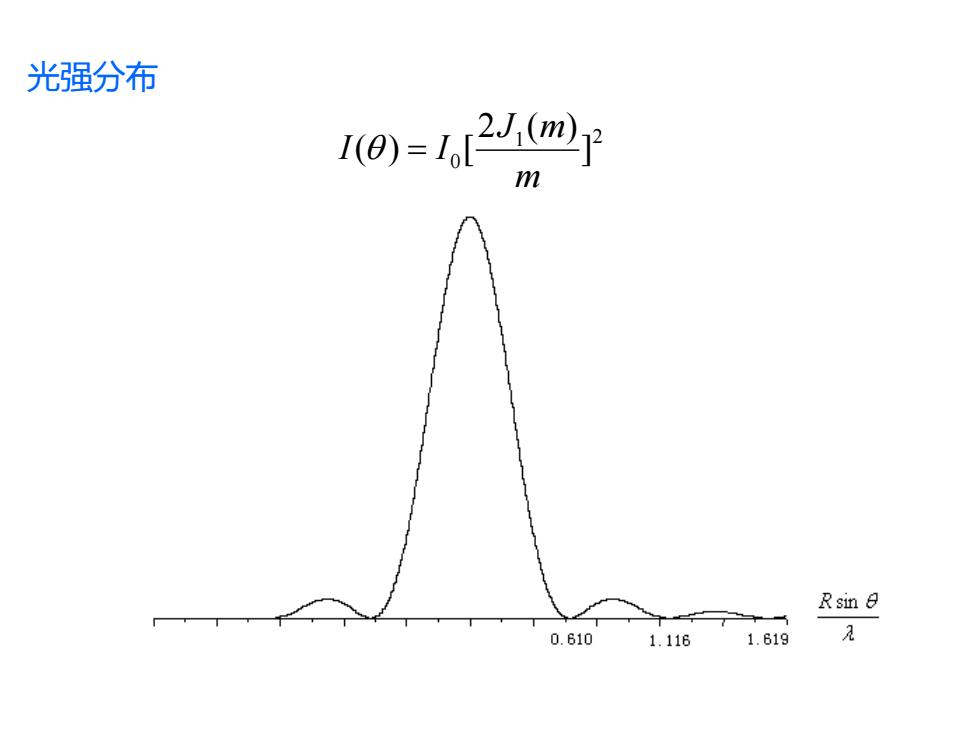
光强分布 1(0=1,20m Rsin 0.610 1.116 1.619 2
光强分布 1 2 0 ] 2 ( ) ( ) [ m J m I = I
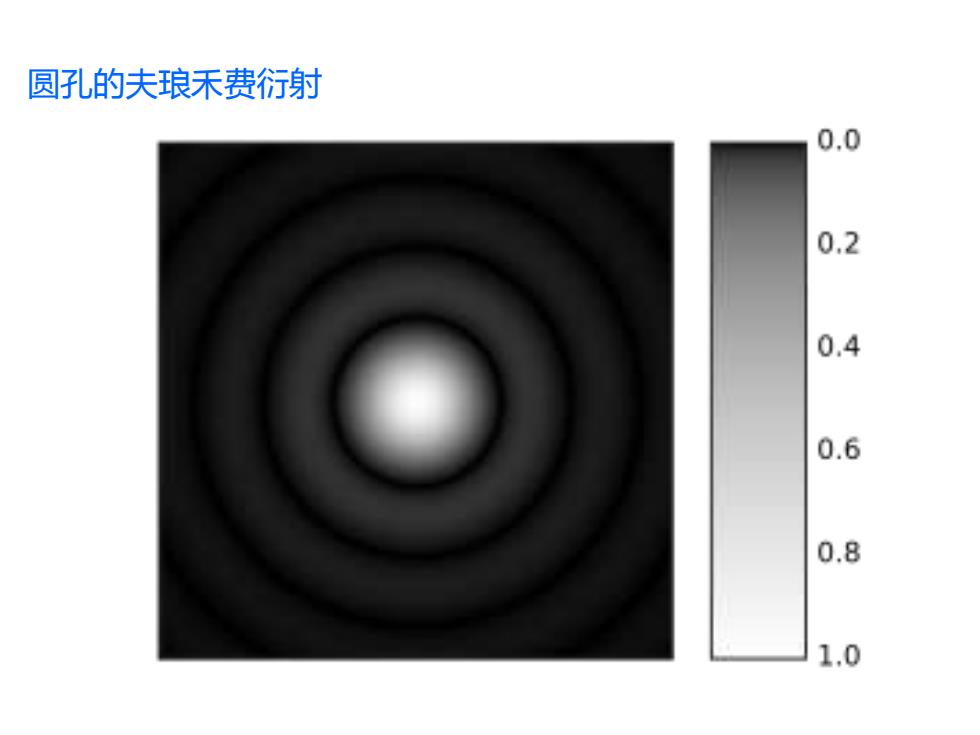
圆孔的夫琅禾费衍射 0.0 0.2 0.4 0.6 0.8 1.0
圆孔的夫琅禾费衍射

圆孔的夫琅禾费衍射 单色光 白光
圆孔的夫琅禾费衍射 单色光 白光

圆孔的夫琅禾费衍射 衍射强度分布
圆孔的夫琅禾费衍射 衍射强度分布

圆孔夫琅禾费衍射图样的特点 ·同心圆环,明暗交错,不等距。 。 中央主极大(零级斑):Aivy斑,占总强度的84%,半 角宽度△0o 48,=061月-12月 R ·圆孔直径为D,透镜焦距f,则Aivy斑半径△1 w-18-128
圆孔夫琅禾费衍射图样的特点 • 同心圆环,明暗交错,不等距。 • 中央主极大(零级斑):Aivry斑,占总强度的84%,半 角宽度 Δθ0 • 圆孔直径为D,透镜焦距f,则Aivry斑半径Δl R D 0 = 0.61 =1.22 0 1.22 f l f D = =