第九讲14种布拉菲格子 旋转对称性 晶系、参考轴 满足点阵条件+晶系不变 初基P单胞(6) 有心化 P点阵中高对称位置加心(体心N, 全面心F,单面心A,B或C双面心) 六方格子特殊心→菱形(三方)单胞 新的点阵 14种布拉菲点阵 (有心8种) 旋转对称性
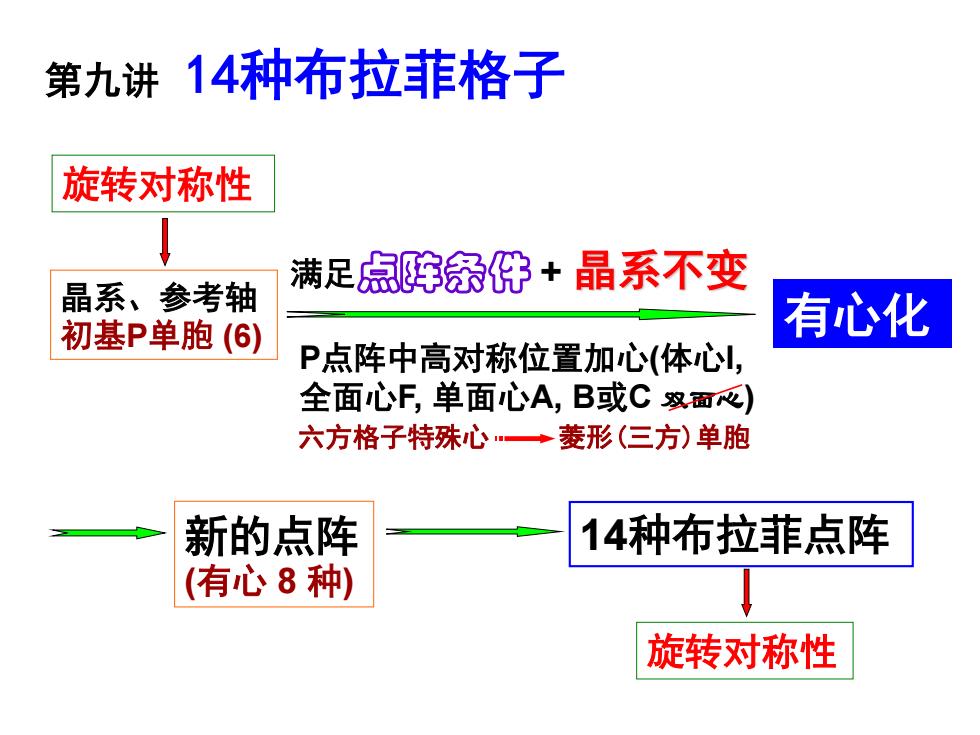
第九讲 14种布拉菲格子 旋转对称性 晶系、参考轴 初基P单胞 (6) 有心化 新的点阵 (有心 8 种) 满足点阵条件 + 晶系不变 14种布拉菲点阵 旋转对称性 P点阵中高对称位置加心(体心I, 全面心F, 单面心A, B或C 双面心) 六方格子特殊心 菱形(三方)单胞
这14种型式最早(1866年) 由Bravias(布拉菲)推得 布拉菲群和和布拉菲点阵 ,又称为布拉维点阵或布拉 加“心” 维点阵型式。 各阵点周围环境相同 x 简单:P 底心:C 侧心:A、B 体心:I 面心:F 不存在两心同时的可能
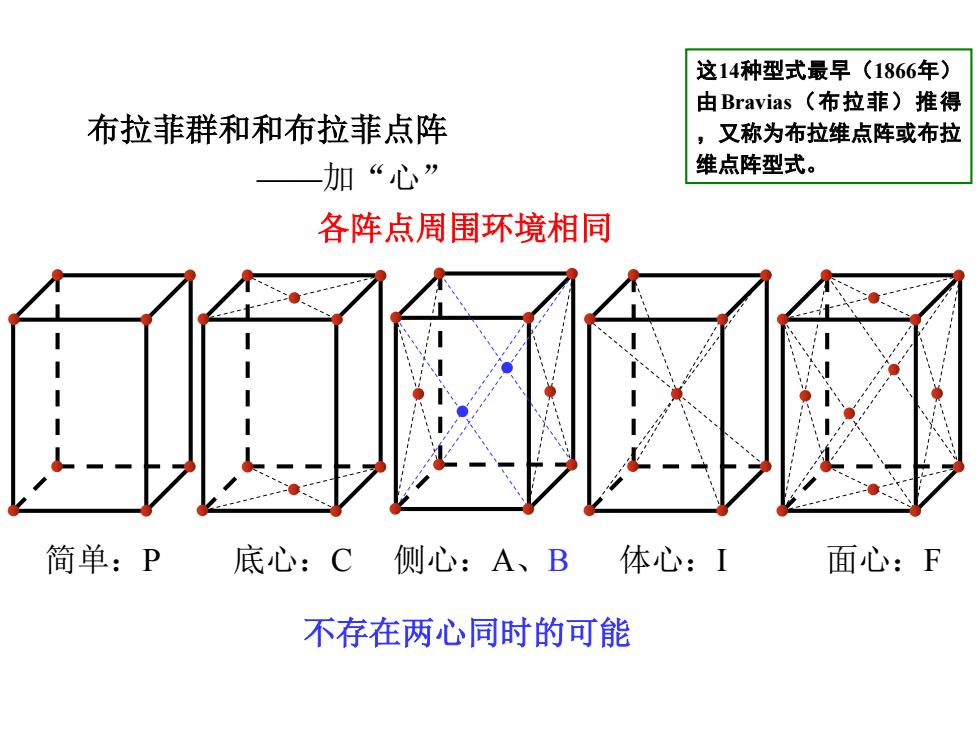
布拉菲群和和布拉菲点阵 ——加“心” 简单:P 底心:C 侧心:A、B 体心:I 面心:F 不存在两心同时的可能 各阵点周围环境相同 这14种型式最早(1866年) 由Bravias(布拉菲)推得 ,又称为布拉维点阵或布拉 维点阵型式

P点阵中高对称位置加心(体心,全面心F, 单面心A,B或C双画心) 双面心不满足点阵条件!
A B X X X X 双面心不满足点阵条件! P点阵中高对称位置加心(体心I, 全面心F, 单面心A, B或C 双面心)

三斜晶系 三斜P 单斜C=P 单斜晶系 ⊕ 单斜B=I=F=A 单斜P 单斜B
三斜晶系单斜晶系 三斜 P 单斜 P 单斜 B 单斜 C = P 单斜 B = I = F = A

正交晶系 正交C=A=B 丰P 正交P 正交0 正交 1 正交F
正交 P 正交 C 正交 I 正交 F 正 交 晶 系 正交 C = A = B ≠ P
四方C=P丰A卡B 四方晶系 四方F=I 非京阵 无A,B 四方P 四方 立方晶系 立方P 立方I,bcc 立方F,fcc 单面心破坏4个3次对称性!非点阵
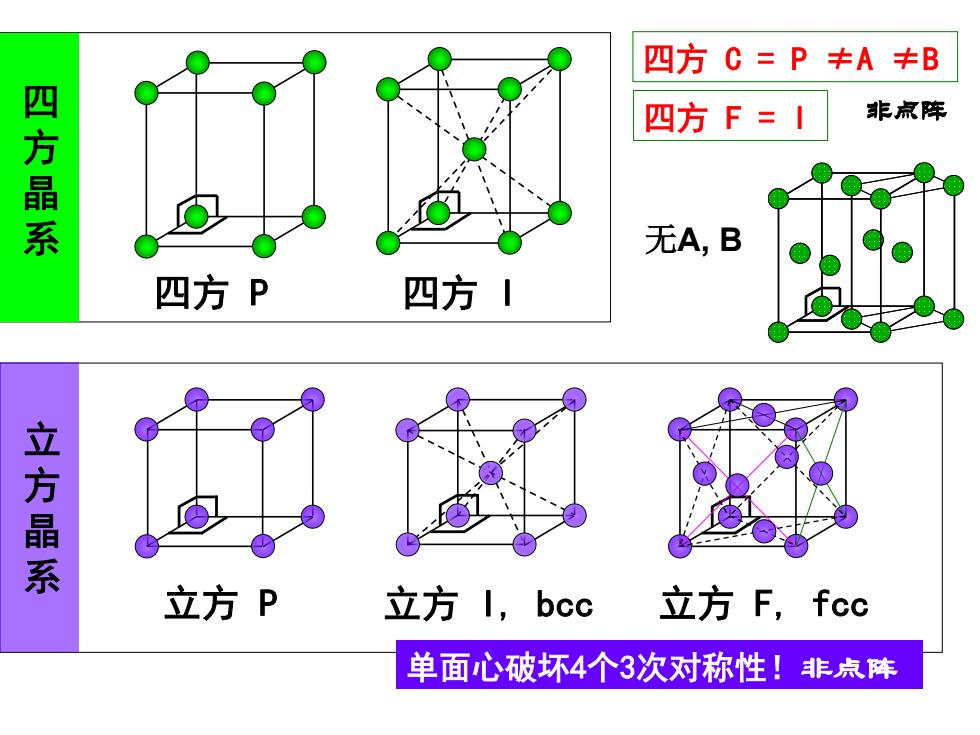
立方 P 立方 I, bcc 立方 F, fcc 四方 P 四方 I 四 方 晶 系 立 方 晶 系 四方 C = P ≠A ≠B 四方 F = I 单面心破坏4个3次对称性!非点阵 非点阵 无A, B
四方 A/mmm a=b≠c,0=B=y=90 A、B 不满足对称性 C→P F→I
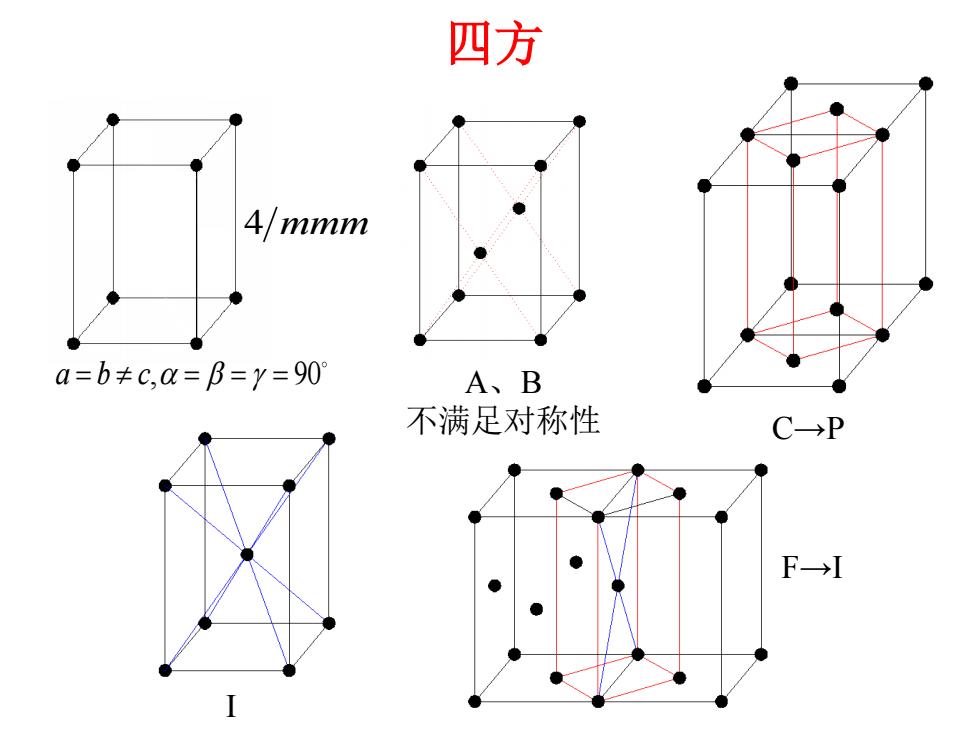
四方 a b c , 90 4 mmm A、B 不满足对称性 C→P I F→I
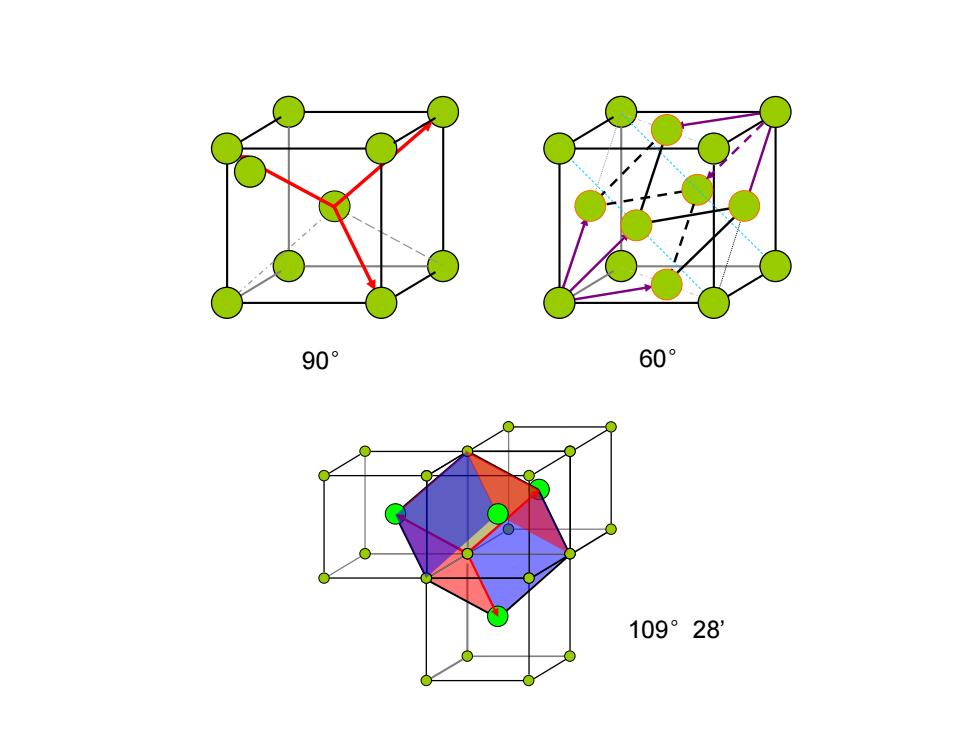
90° 60° 109°28
60° 109°28’ 90°

有心化 +c/2 六方晶系 ● 康面心:正交 侧面心:非点阵 六方P Q ●+c/2 体心:非六方点阵 (113,2/3,0):P 三方菱形晶系 +c/3 0+2c/3 ±(2/3,113,1/3):R 三方R ±(113,213,113):R
六 方 晶 系 三 方 菱 形 晶 系 六方 P 三方 R 底面心:正交 侧面心:非点阵 +c/2 体心:非六方点阵 +c/2 (1/3, 2/3, 0):P +2c/3 +c/3 ±(2/3, 1/3, 1/3):R 有心化 ±(1/3, 2/3, 1/3):R
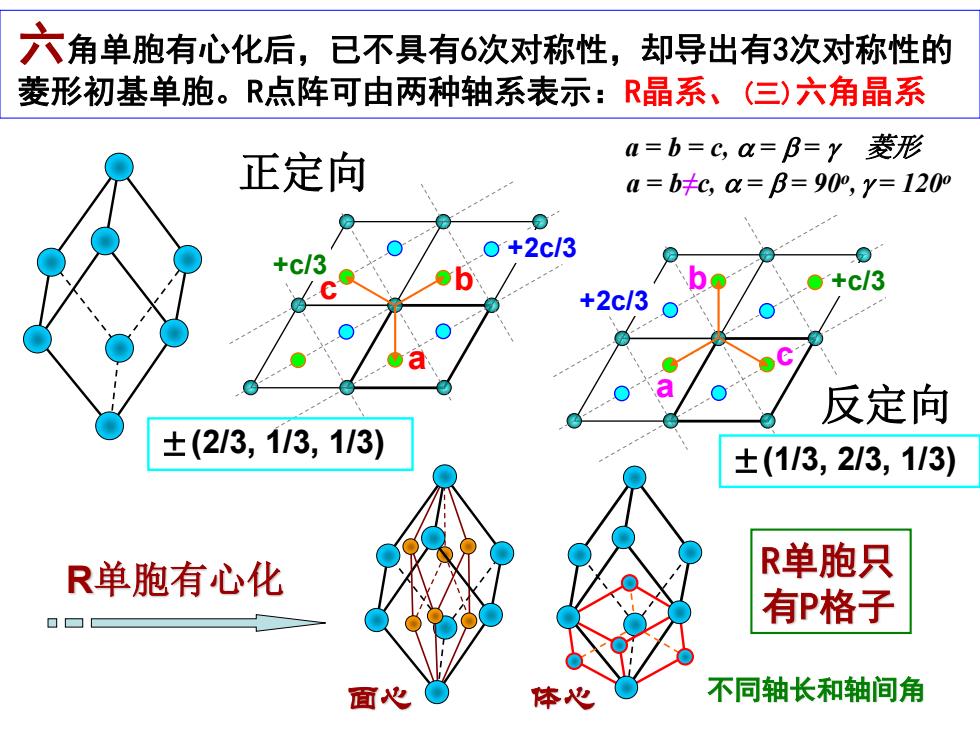
六角单胞有心化后, 已不具有6次对称性,却导出有3次对称性的 菱形初基单胞。R点阵可由两种轴系表示:R晶系、(三)六角晶系 a=b=c,a=B=y菱形 正定向 a=b+c,a=B=90,y=1200 0 O+2c/3 +c/3 b +c/3 +2c/3 a 反定向 ±(2/3,113,113) ±(113,2/3,113) R单胞有心化 R单胞只 有P格子 面 体必 不同轴长和轴间角
+2c/3 +c/3 a c b 正定向 +c/3 +2c/3 a b c 反定向 六角单胞有心化后,已不具有6次对称性,却导出有3次对称性的 菱形初基单胞。R点阵可由两种轴系表示:R晶系、(三)六角晶系 a = b≠c, = = 90o , = 120o a = b = c, = = 菱形 R单胞有心化 面心 体心 R单胞只 有P格子 不同轴长和轴间角 ±(2/3, 1/3, 1/3) ±(1/3, 2/3, 1/3)