
第四章光的衍射
第四章 光的衍射

4.1光的衍射现象和惠更斯-费涅耳原理 光的衍射现象 惠更斯-费涅耳原理,基尔霍夫边界条件 巴俾涅原理 衍射的分类
4.1 光的衍射现象和惠更斯-费涅耳原理 光的衍射现象 惠更斯-费涅耳原理,基尔霍夫边界条件 巴俾涅原理 衍射的分类

一、光的衍射现象 衍射(Diffraction):当波动遇到障碍时,能够绕过障碍物 并在其后的几何阴影区内造成一定的强度分布,这种偏离直 线传播的现象称为衍射。(不能用反射和折射解释的绕射现 象) 水波的衍射 思考:光波既然是波,为什么在实际生活中比较难观察到?
一、 光的衍射现象 衍射(Diffraction):当波动遇到障碍时,能够绕过障碍物, 并在其后的几何阴影区内造成一定的强度分布,这种偏离直 线传播的现象称为衍射。(不能用反射和折射解释的绕射现 象) 水波的衍射 思考:光波既然是波,为什么在实际生活中比较难观察到?

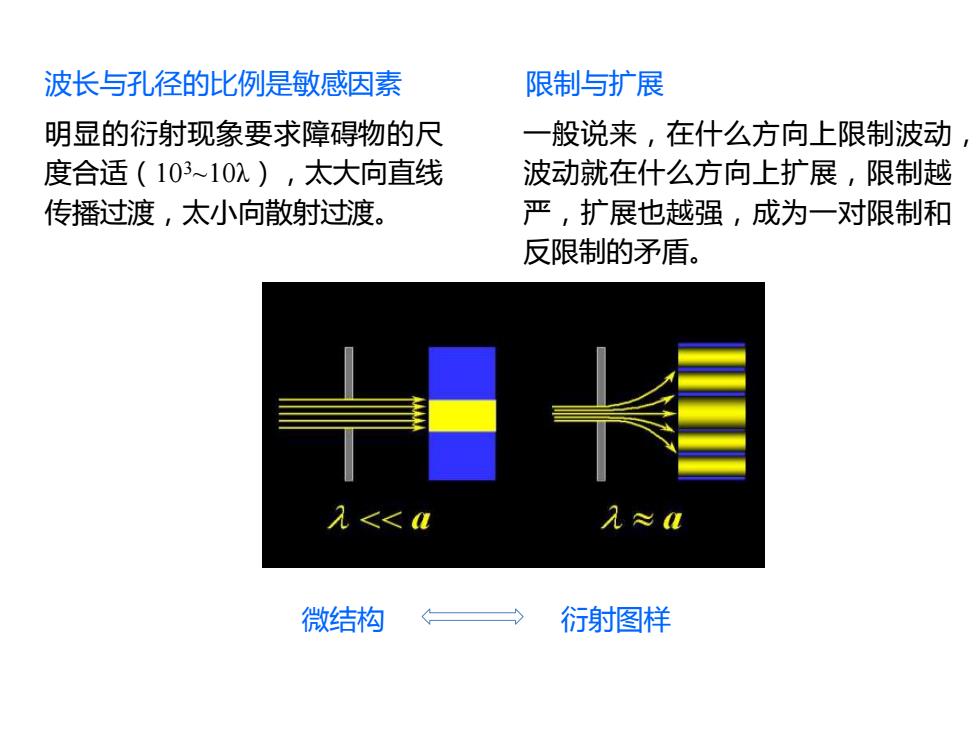
波长与孔径的比例是敏感因素 限制与扩展 明显的衍射现象要求障碍物的尺 一般说来,在什么方向上限制波动 度合适(10310,),太大向直线 波动就在什么方向上扩展,限制越 传播过渡,太小向散射过渡。 严,扩展也越强,成为一对限制和 反限制的矛盾。 2<< 见≈ 微结构 衍射图样
明显的衍射现象要求障碍物的尺 度合适(103~10λ),太大向直线 传播过渡,太小向散射过渡。 一般说来,在什么方向上限制波动, 波动就在什么方向上扩展,限制越 严,扩展也越强,成为一对限制和 反限制的矛盾。 波长与孔径的比例是敏感因素 限制与扩展 微结构 衍射图样
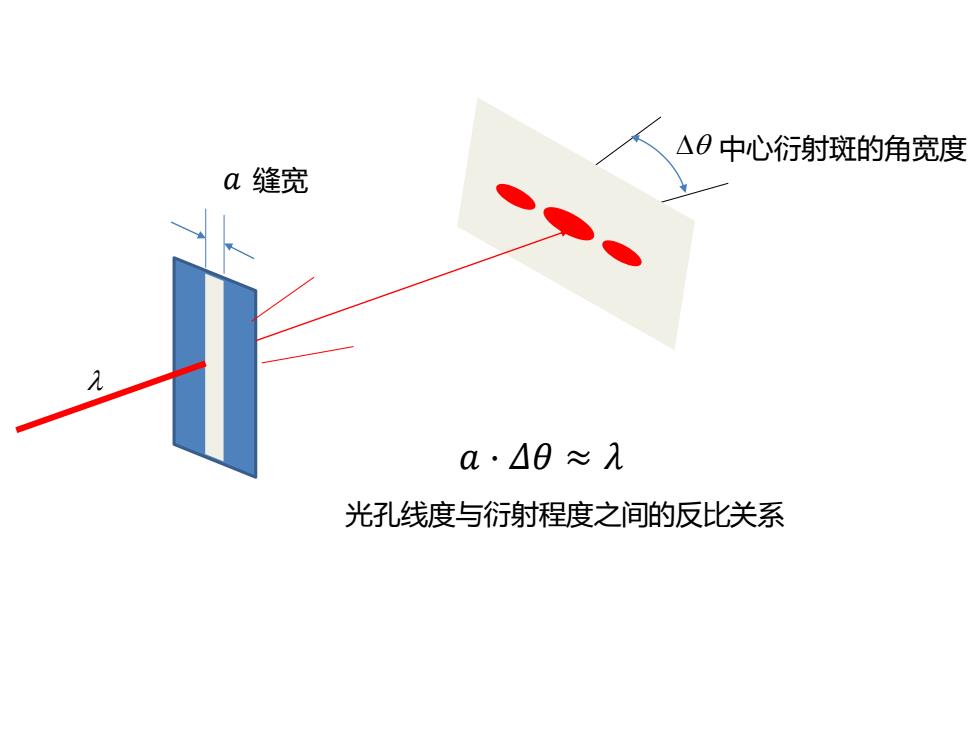
△B中心衍射斑的角宽度 a缝宽 a·△0≈λ 光孔线度与衍射程度之间的反比关系
缝宽 中心衍射斑的角宽度 光孔线度与衍射程度之间的反比关系 𝑎 · 𝛥𝜃 ≈ 𝜆 𝑎
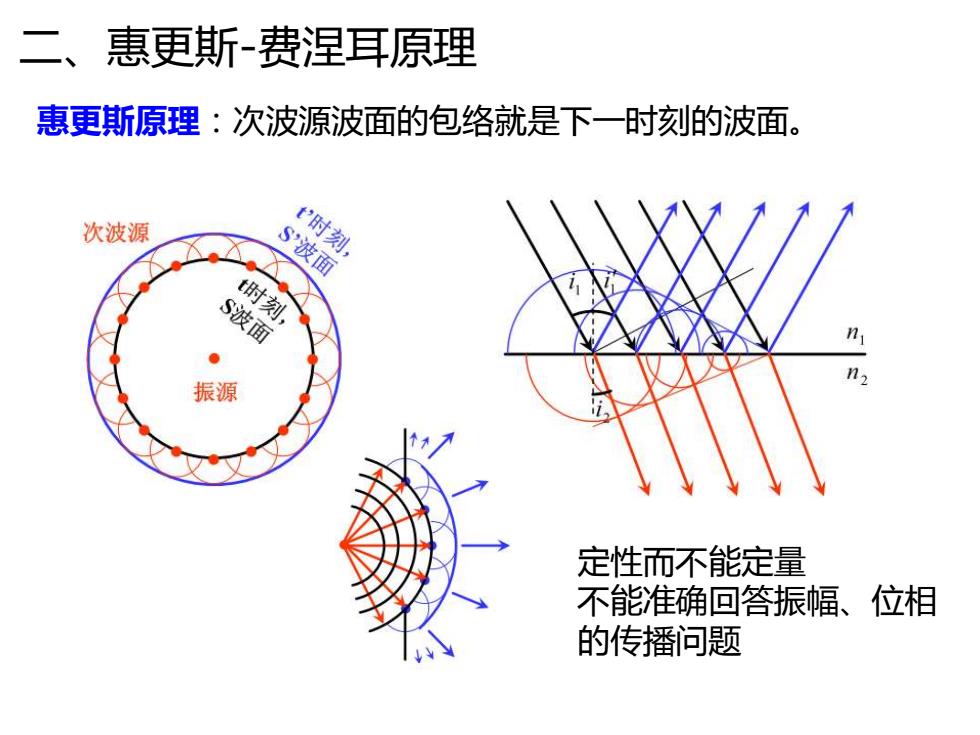
二、惠更斯-费涅耳原理 惠更斯原理:次波源波面的包络就是下一时刻的波面。 次波源 t时刻, S波面 t时刻, S波面 n2 振源 定性而不能定量 不能准确回答振幅、位相 的传播问题
二、惠更斯-费涅耳原理 惠更斯原理:次波源波面的包络就是下一时刻的波面。 定性而不能定量 不能准确回答振幅、位相 的传播问题
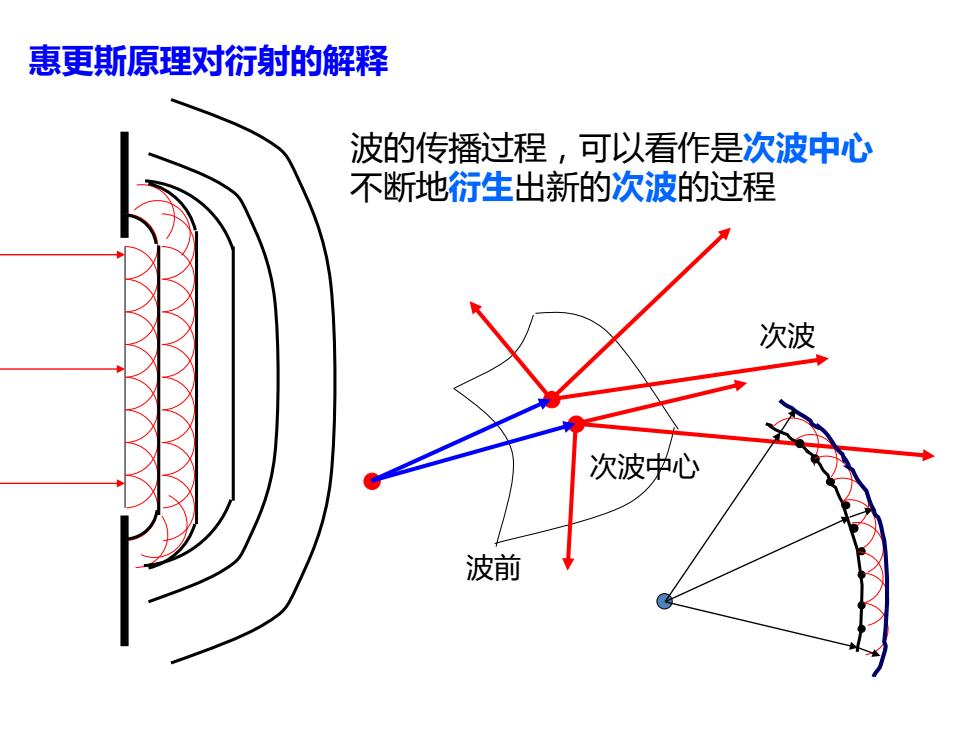
惠更斯原理对衍射的解释 波的传播过程,可以看作是次波中心 不断地衍生出新的次波的过程 次波 次波中心 波前
惠更斯原理对衍射的解释 波前 次波中心 次波 波的传播过程,可以看作是次波中心 不断地衍生出新的次波的过程
惠更斯的次波概念 继承 补充和发展 次波相干叠加 提出 吸取 菲涅耳 惠更斯一菲涅耳原理 (1788-1827) 光波干涉概念 衍射理论框架
惠更斯的次波概念 光波干涉概念 继承 吸取 补充和发展 提出 次波相干叠加 惠更斯—菲涅耳原理 衍射理论框架 菲涅耳 (1788-1827)
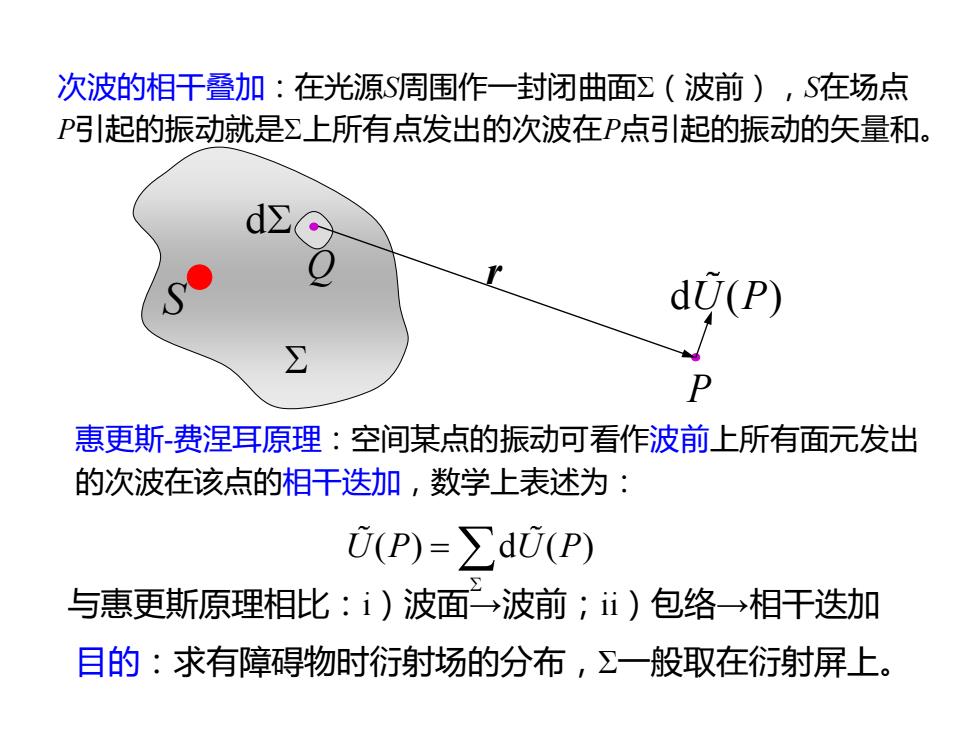
次波的相干叠加:在光源S周围作一封闭曲面Σ(波前),S在场点 P引起的振动就是Σ上所有点发出的次波在P点引起的振动的矢量和。 d(P) 惠更斯费涅耳原理:空间某点的振动可看作波前上所有面元发出 的次波在该点的相干迭加,数学上表述为: U(P)=∑dU(P) 与惠更斯原理相比:i)波面→波前;i)包络→相干迭加 目的:求有障碍物时衍射场的分布,Σ一般取在衍射屏上
惠更斯-费涅耳原理:空间某点的振动可看作波前上所有面元发出 的次波在该点的相干迭加,数学上表述为: 次波的相干叠加:在光源S周围作一封闭曲面Σ(波前),S在场点 P引起的振动就是Σ上所有点发出的次波在P点引起的振动的矢量和。 P Q d r S d ( ) U P U P U P ( ) d ( ) = 与惠更斯原理相比:i)波面→波前;ii)包络→相干迭加 目的:求有障碍物时衍射场的分布,Σ一般取在衍射屏上