
2.2光波的叠加 光的叠加方法 光的叠加强度 波包
光的叠加方法 光的叠加强度 波包 2.2 光波的叠加

两列波在空间相遇
两列波在空间相遇

相遇后,仍然独自传播 若是粒子相遇,则将发生碰撞,各自的状 态都将改变 woW
相遇后,仍然独自传播 • 若是粒子相遇,则将发生碰撞,各自的状 态都将改变
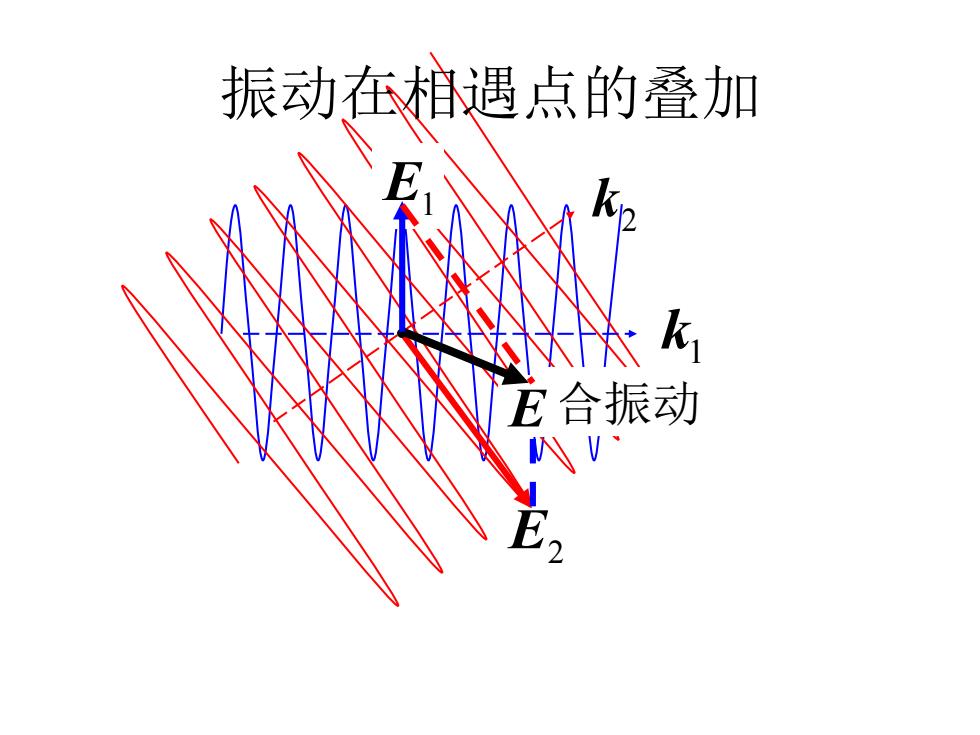
振动在相遇点的叠加 E合振动
振动在相遇点的叠加 k1 2 E1 k E2 E 合振动

光的叠加原理 。1.波的独立传播定律·2.波的叠加原理 。 不同的波列波在空·几列波在相遇点所 间相遇时,如扰动 引起的扰动是各列 不十分强,各列波 波独自在该点所引 将保持各自的特性 起的扰动的叠加 不变,继续传播, (矢量的线性叠加, 相互之间没有影响。矢量和)
一、 光的叠加原理 • 1.波的独立传播定律 • 不同的波列波在空 间相遇时,如扰动 不十分强,各列波 将保持各自的特性 不变,继续传播, 相互之间没有影响。 • 2.波的叠加原理 • 几列波在相遇点所 引起的扰动是各列 波独自在该点所引 起的扰动的叠加 (矢量的线性叠加, 矢量和)

成立的条件 ·传播介质为线性介质。 。 振动不十分强。在振动很强烈时,线性介 质会变为非线性的。 注意要点:不是强度的叠加,也不是振幅 的简单相加,而是振动矢量(瞬时值)的 叠加。 对于电磁波,就是电场强度(电场分量, 光矢量)、磁场强度的叠加
成立的条件 • 传播介质为线性介质。 • 振动不十分强。在振动很强烈时,线性介 质会变为非线性的。 • 注意要点:不是强度的叠加,也不是振幅 的简单相加,而是振动矢量(瞬时值)的 叠加。 • 对于电磁波,就是电场强度(电场分量, 光矢量)、磁场强度的叠加

二、定态光波叠加的方法 ·对于同频率、同振动方向的单色光 ·1.代数法:瞬时值叠加 Wi(P)=A cos[(P)-@t]w2(P)=A(P)cos[(P)-ot] 合振动W=必1+必2=A(P)cos[p(P)-o] 振幅 A(P)=+A+2A4c0s(02-0) 相位anoP)= A(P)sin(P)+A2(P)sin2 (P) 4(P)cos(P)+A(P)cos2(P) 叠加之后,仍然是原频率的定态光波
二、定态光波叠加的方法 • 对于同频率、同振动方向的单色光 • 1.代数法:瞬时值叠加 1 1 1 ( ) cos[ ( ) ] P A P t = − 2 2 2 ( ) ( )cos[ ( ) ] P A P P t = − =1 + 2 2 2 2 1 2 1 2 2 1 A P A A A A ( ) 2 cos( ) = + + − 1 1 2 2 1 1 2 2 ( )sin ( ) ( )sin ( ) tan ( ) ( )cos ( ) ( )cos ( ) A P P A P P P A P P A P P + = + 合振动 = A P P t ( )cos[ ( ) ] − 振幅 相位 叠加之后,仍然是原频率的定态光波
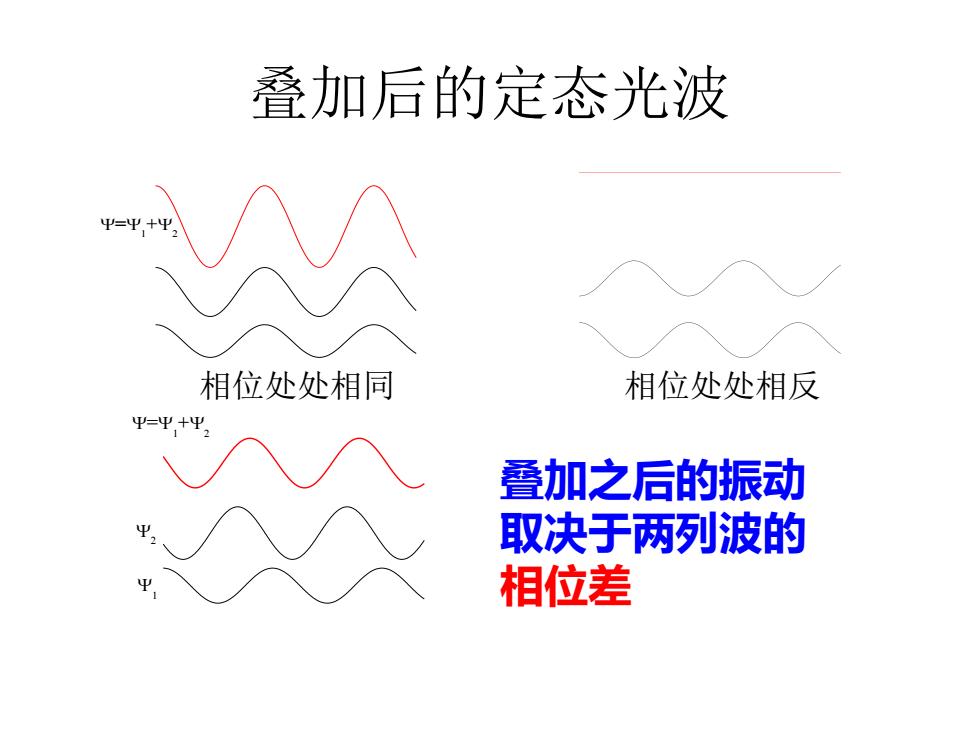
叠加后的定态光波 相位处处相同 相位处处相反 =Ψ,+ 叠加之后的振动 取决于两列波的 相位差
=+ 相位处处相同 相位处处相反 叠加后的定态光波 =+ 叠加之后的振动 取决于两列波的 相位差

由瞬时值所引出的矢量方法 w(P)=A(P)cos[(P)-@t]w(P)=A(P)cos[(P)-ot] 业=以1+2=A(P)cos[p(P)-ot] A2(P)=A2+4+244 cos(2-) ·合振动的振幅与两列波的振幅之间满足余 孩公式 P2一1
2 1 − 由瞬时值所引出的矢量方法 • 合振动的振幅与两列波的振幅之间满足余 弦公式 2 2 2 1 2 1 2 2 1 A (P) = + + − A A A 2 co A s( ) 1 1 1 ( ) ( )cos[ ( ) ] P A P P t = − 2 2 2 ( ) ( )cos[ ( ) ] P A P P t = − = + 1 2 = A P P t ( )cos[ ( ) ] − A A1 A2

·2.复数法:复振幅相加 VAe(=Aee ior=Ue-ior 2=A)=Acc-or=U,e-tor U=detm U2 =4el 0=听1+2=U,eor+02eo=(0,+j2)eio =U+0,=Ae+4e:=Aeto 振幅和相位的表达式与代数方法相同
• 2.复数法 :复振幅相加 1 1 1e i U A = 2 2 2e i U A = 1 2 1 2 e e i i A A = + 振幅和相位的表达式与代数方法相同 1 2 ~ ~ ~ U =U +U e i A = 2 2 ( ) 2 2 2 2 e e e e i t i i t i t A A U − − − = = = 1 1 ( ) 1 1 1 1 e e e e i t i i t i t A A U − − − = = = 1 2 1 2 1 2 e e ( )e i t i t i t U U U U − − − = + = + = +