
5.3偏振光的获得与检验 偏振光回顾 椭圆偏振光的获得 椭圆偏振光的检验
5.3 偏振光的获得与检验 偏振光回顾 椭圆偏振光的获得 椭圆偏振光的检验

一、 偏振光回顾 正交振动平面偏振光(线偏振光)的合成 假设:两同向传播的线偏振光波,频率为。,相位差为δ,振动方 向分别沿x和y方向,振幅分别为A和A,瞬时光矢量分别为 E,=A,cosot,E=A,cos(@t+8) (E.=cos@t 其归一化形式为 A os)=cosco-sinrsin A 两式相减得到 EE cos=-sin@tsin A.A. 消除o,得到合成光矢量末 E+-25,Ec0s=sin2 端轨迹方程
一、偏振光回顾 正交振动平面偏振光(线偏振光)的合成 假设:两同向传播的线偏振光波,频率为w,相位差为d,振动方 向分别沿x和y方向,振幅分别为Ax和Ay ,瞬时光矢量分别为 cos , cos( ) E A t E A t x x y y = = + w w d ( ) cos cos cos cos sin sin x x y y E t A E t t t A w w d w d w d = = + = − 其归一化形式为 cos sin sin y x y x E E t A A 两式相减得到 − = − d w d 2 2 2 2 2 2 cos sin x y x y x y x y E E E E A A A A + − = d d 消除wt,得到合成光矢量末 端轨迹方程

正交振动平面偏振光的合成 意义:合光矢量末端的轨迹为一个椭圆,该椭圆与以Ex=士Ax 和E,=士A,为界的矩形框内切,其旋转方向及长短轴的方位与 两叠加光波的相位差6有关。 E2EEE -cos&sin28 @t 椭圆偏振光产生于两同频率、相位差 恒定且振动方向正交的线偏振光的叠 加,线偏振光和圆偏振光都可看做椭 圆偏振光的特例。 正交振动的合成
正交振动平面偏振光的合成 意义:合光矢量末端的轨迹为一个椭圆,该椭圆与以Ex =±Ax 和Ey =±Ay为界的矩形框内切,其旋转方向及长短轴的方位与 两叠加光波的相位差d 有关。 正交振动的合成 x Ey Ex y wt Ay Ax 2 2 2 2 2 2 cos sin x y x y x y x y E E E E A A A A + − = d d 椭圆偏振光产生于两同频率、相位差 恒定且振动方向正交的线偏振光的叠 加,线偏振光和圆偏振光都可看做椭 圆偏振光的特例
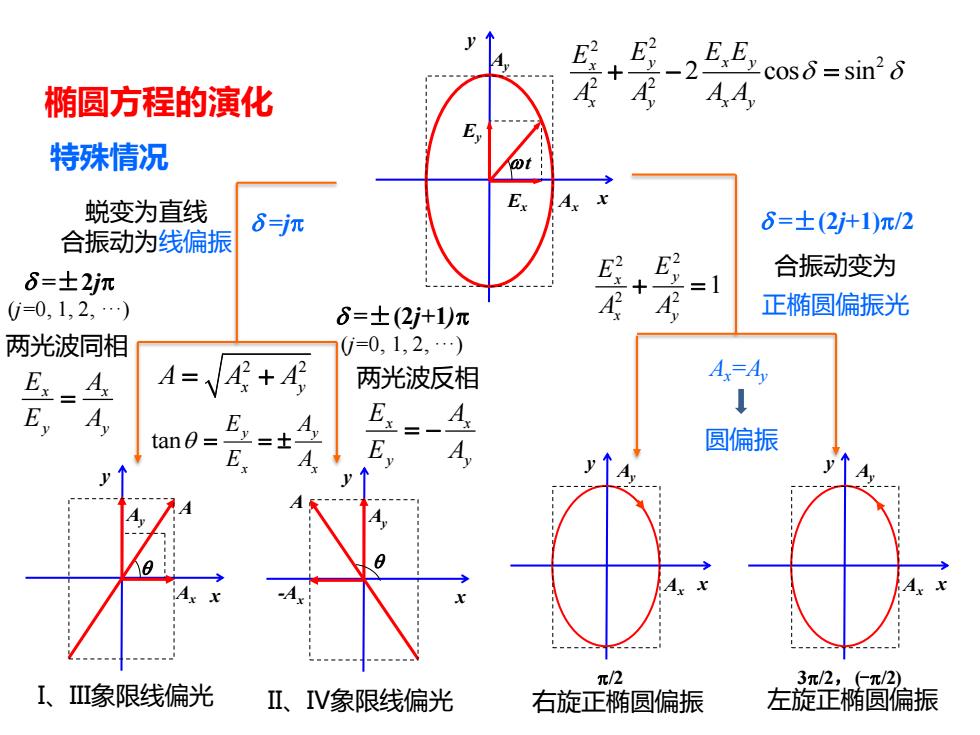
椭圆方程的演化 特殊情况 蜕变为直线 6=j沉 6=土(2j+1)π/2 合振动为线偏振 6=士2jπ + 合振动变为 0=0,1,2,.) 8=土(2j+1)π A + 正椭圆偏振光 两光波同相 0=0,1,2,.) E=4 4=4+ Ax=Ay 1 两光波反相 tan= =土 Ay E=-4 圆偏振 E π/2 3π/2,(-π/2) I、I象限线偏光 Ⅱ、IV象限线偏光 右旋正椭圆偏振 左旋正椭圆偏振
椭圆方程的演化 x Ey Ex y wt Ay Ax x A y q Ay Ax x A y q Ay -Ax 2 2 2 2 2 2 cos sin x y x y x y x y E E E E A A A A + − = d d p/2 x y Ay Ax 3p/2,(-p/2) x y Ay Ax d =±2jp (j=0, 1, 2, ···) 两光波同相 x x y y E A E A = d =±(2j+1)p (j=0, 1, 2, ···) 两光波反相 x x y y E A E A = − d =±(2j+1)p/2 合振动变为 正椭圆偏振光 2 2 2 2 1 x y x y E E A A + = 特殊情况 右旋正椭圆偏振 左旋正椭圆偏振 蜕变为直线 合振动为线偏振 2 2 A A A = +x y tan y y x x E A E A q = = Ax=Ay 圆偏振 d =jp I、III象限线偏光 II、IV象限线偏光
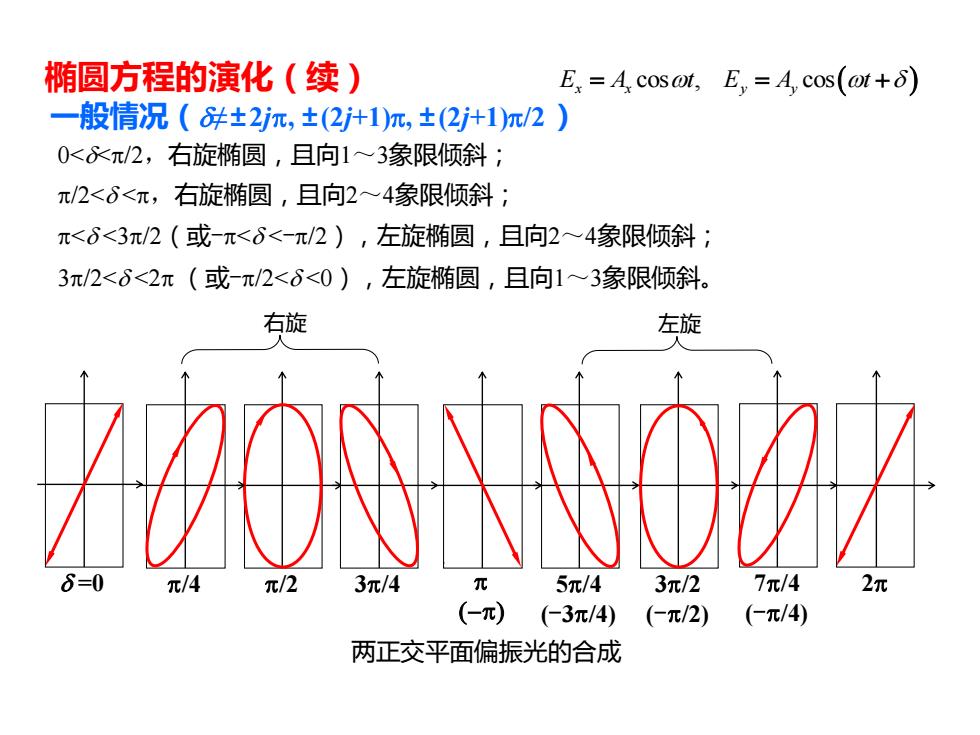
椭圆方程的演化(续) E=A cos@t,E=A,cos(@t+) 一般情况(#±2j元,±(2j+1)m,±(2j+1)元/2) 0<元/2,右旋椭圆,且向1~3象限倾斜: π/2<6<π,右旋椭圆,且向2~4象限倾斜; π<6<3π/2(或-π<6<-元/2),左旋椭圆,且向2~4象限倾斜; 3π/2<6<2π(或-π/2<6<0),左旋椭圆,且向1~3象限倾斜。 右旋 左旋 6=0 元/4 π/2 3π/4 元 5π/43π/27π/4 2元π (-)(-3π/4) (-π/2) (-元/4) 两正交平面偏振光的合成
椭圆方程的演化(续) 一般情况(d≠±2jp, ±(2j+1)p, ±(2j+1)p/2 ) 右旋 左旋 p/2 3p/2 (-p/2) p/4 7p/4 (-p/4) 3p/4 5p/4 (-3p/4) d =0 p 2p (−p) 两正交平面偏振光的合成 0<d<p/2,右旋椭圆,且向1~3象限倾斜; p/2<d <p,右旋椭圆,且向2~4象限倾斜; p<d <3p/2(或-p<d <-p/2),左旋椭圆,且向2~4象限倾斜; 3p/2<d <2p (或-p/2<d <0),左旋椭圆,且向1~3象限倾斜。 cos , cos( ) E A t E A t x x y y = = + w w d
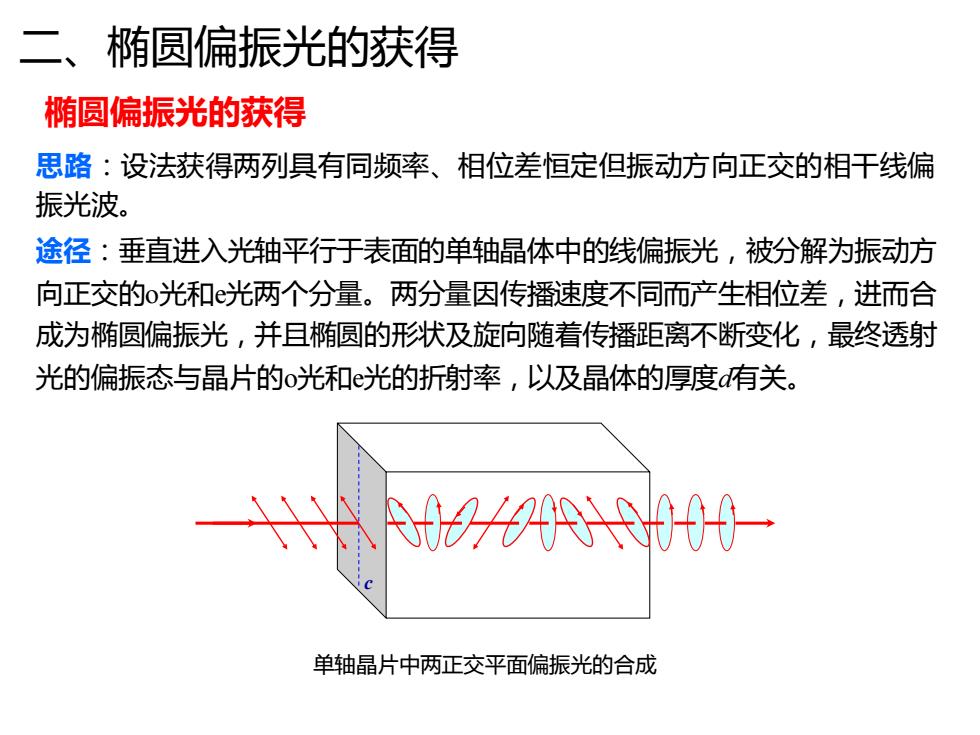
二、椭圆偏振光的获得 椭圆偏振光的获得 思路:设法获得两列具有同频率、相位差恒定但振动方向正交的相干线偏 振光波。 途径:垂直进入光轴平行于表面的单轴晶体中的线偏振光,被分解为振动方 向正交的o光和光两个分量。两分量因传播速度不同而产生相位差,进而合 成为椭圆偏振光,并且椭圆的形状及旋向随着传播距离不断变化,最终透射 光的偏振态与晶片的o光和光的折射率,以及晶体的厚度d有关。 00 单轴晶片中两正交平面偏振光的合成
二、椭圆偏振光的获得 椭圆偏振光的获得 思路:设法获得两列具有同频率、相位差恒定但振动方向正交的相干线偏 振光波。 途径:垂直进入光轴平行于表面的单轴晶体中的线偏振光,被分解为振动方 向正交的o光和e光两个分量。两分量因传播速度不同而产生相位差,进而合 成为椭圆偏振光,并且椭圆的形状及旋向随着传播距离不断变化,最终透射 光的偏振态与晶片的o光和e光的折射率,以及晶体的厚度d有关。 c 单轴晶片中两正交平面偏振光的合成

(1)自然光经过波片 (a)自然光可以正交分解。 (b)每一个分量都含有相位随机的多列平面波。 (c)每列平面波在晶体中分为相互正交的o光、e光。 (d)经过波片后,每一个分量仍然是相位随机的多列波。 (e)所以,正交分量合成后,仍是自然光。 ()如果不考虑波片的吸收,可以认为光强不变
(1)自然光经过波片 (a)自然光可以正交分解。 (b)每一个分量都含有相位随机的多列平面波。 (c)每列平面波在晶体中分为相互正交的o光、e光。 (d)经过波片后,每一个分量仍然是相位随机的多列波。 (e)所以,正交分量合成后,仍是自然光。 (f)如果不考虑波片的吸收,可以认为光强不变
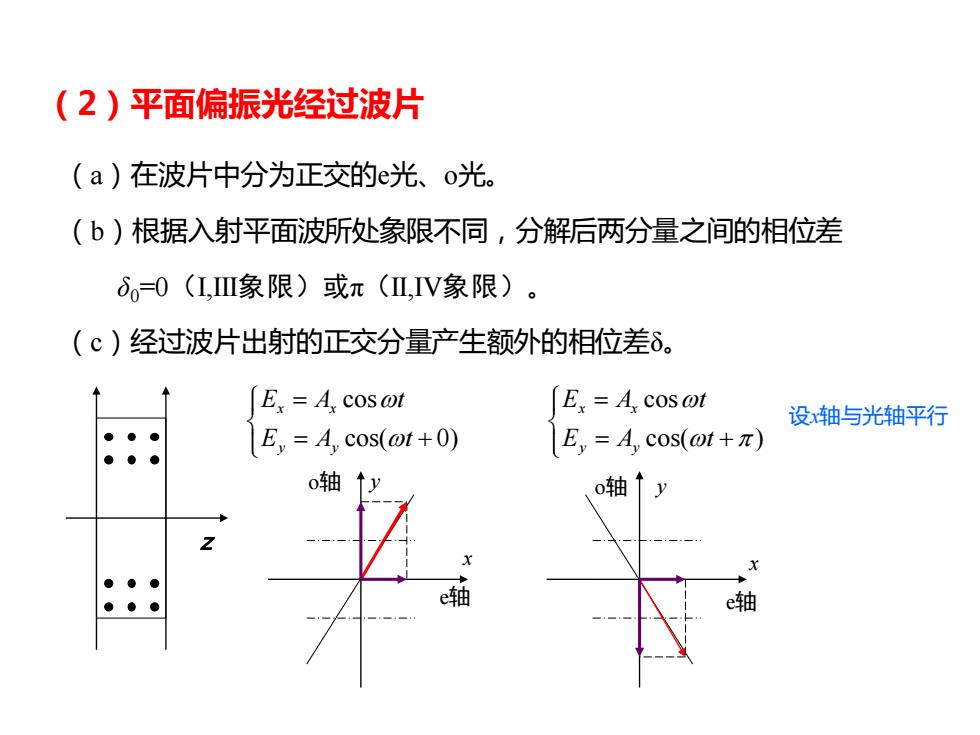
(2)平面偏振光经过波片 (a)在波片中分为正交的e光、o光。 (b)根据入射平面波所处象限不同,分解后两分量之间的相位差 6=0(I,Ⅲ象限)或π(L,IV象限)。 (c)经过波片出射的正交分量产生额外的相位差δ。 E =A,cosot E,=A.cosot 设轴与光轴平行 ●●● E=A cos(@t+0) E,=A,cos(ot+π) ●●● o轴↑y 0轴↑ ●●● ●● e轴 轴
(2)平面偏振光经过波片 (a)在波片中分为正交的e光、o光。 (b)根据入射平面波所处象限不同,分解后两分量之间的相位差 δ0=0(I,III象限)或π(II,IV象限)。 (c)经过波片出射的正交分量产生额外的相位差δ。 cos cos( 0) x x y y E A t E A t w w = = + cos cos( ) x x y y E A t E A t w w p = = + y e轴 o轴 x e轴 o轴 x y z 设x轴与光轴平行

(2)平面偏振光经过波片(续) ①d=0:6=0,合成光波仍为偏振面与入射光重合的线偏振光。 ②d=入(最小厚度的4片):士/2(n。>n取正号,n。<n取负 4no-nel 号),合成光波为正椭圆偏振光。其旋转方向不仅与n,与n之间的关系有关, 还与输入偏振光的初始状态有关。 例:同样在)轴是快轴的情况下,初始相位差为0和π情况下的出射光场偏振状态。 E=A,cosot E,=A cosot 右旋椭圆 E=A,cos(@t+0) E=4,cos(ot+ 偏振光 E =A,cosot E.=A,cosot 左旋椭圆 E,=A,cos(ot+π) E,=,coo- 偏振光
① d=0:d=0,合成光波仍为偏振面与入射光重合的线偏振光。 ② 𝑑 = 𝜆 4 𝑛𝑜−𝑛𝑒 (最小厚度的l/4片):d=±p/2(no>ne取正号,no<ne取负 号) ,合成光波为正椭圆偏振光。其旋转方向不仅与no与ne之间的关系有关, 还与输入偏振光的初始状态有关。 cos cos( 0) x x y y E A t E A t w w = = + cos cos( ) 2 x x y y E A t E A t w p w = = + 右旋椭圆 偏振光 cos cos( ) x x y y E A t E A t w w p = = + cos cos( ) 2 x x y y E A t E A t w p w = = − 左旋椭圆 偏振光 (2)平面偏振光经过波片(续) 例:同样在y轴是快轴的情况下,初始相位差为0和p情况下的出射光场偏振状态
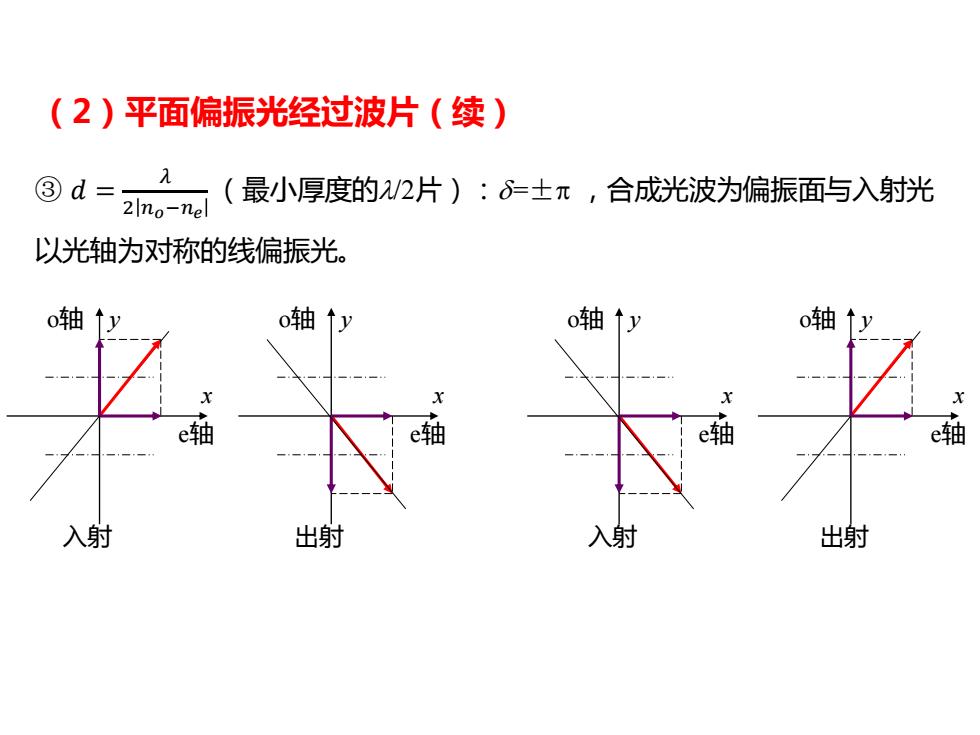
(2)平面偏振光经过波片(续) ③d= (最小厚度的/2片):6-士π,合成光波为偏振面与入射光 2 no-nel 以光轴为对称的线偏振光。 o轴↑y o轴↑y o轴1y o轴 X e轴 e轴 e轴 e轴 入射 出射 入射 出射
③ 𝑑 = 𝜆 2 𝑛𝑜−𝑛𝑒 (最小厚度的l/2片):d=±p ,合成光波为偏振面与入射光 以光轴为对称的线偏振光。 e轴 o轴 x y e轴 o轴 x y e轴 o轴 x y e轴 o轴 x y 入射 出射 入射 出射 (2)平面偏振光经过波片(续)