
4.3夫琅禾费单缝衍射 实验装置 单缝衍射的强度公式和衍射图案 单缝衍射因子的特点
4.3夫琅禾费单缝衍射 实验装置 单缝衍射的强度公式和衍射图案 单缝衍射因子的特点

一、 实验装置 夫琅和费 (Joseph von Fraunhofer 1787-1826) 德国物理学家 ·发现并研究了太阳光谱中的暗线 ·设计和制造了消色差透镜 ·首创用牛顿环方法检查光学表面加工精度及透镜形状 ·首先定量地研究了衍射光栅,并用其测量光的波长 ·给出了光栅方程
一、实验装置 夫琅和费 (Joseph von Fraunhofer 1787—1826) 德国物理学家 • 发现并研究了太阳光谱中的暗线 • 设计和制造了消色差透镜 • 首创用牛顿环方法检查光学表面加工精度及透镜形状 • 首先定量地研究了衍射光栅,并用其测量光的波长 • 给出了光栅方程
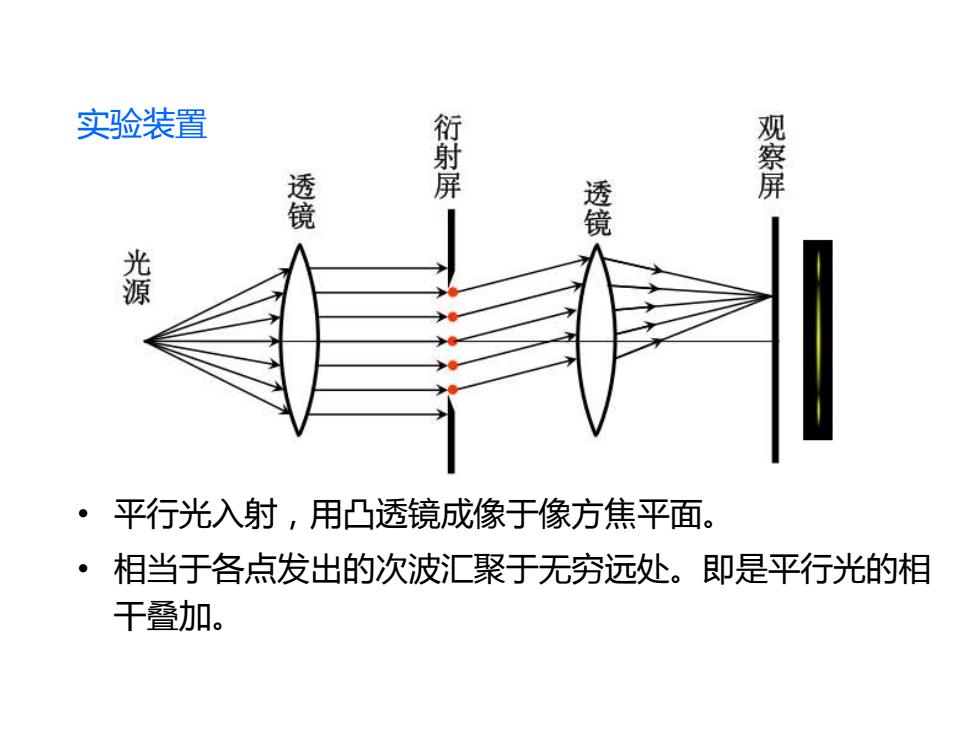
实验装置 衍射屏 观察屏 镜 ·平行光入射,用凸透镜成像于像方焦平面。 ·相当于各点发出的次波汇聚于无穷远处。即是平行光的相 干叠加
• 平行光入射,用凸透镜成像于像方焦平面。 • 相当于各点发出的次波汇聚于无穷远处。即是平行光的相 干叠加。 实验装置
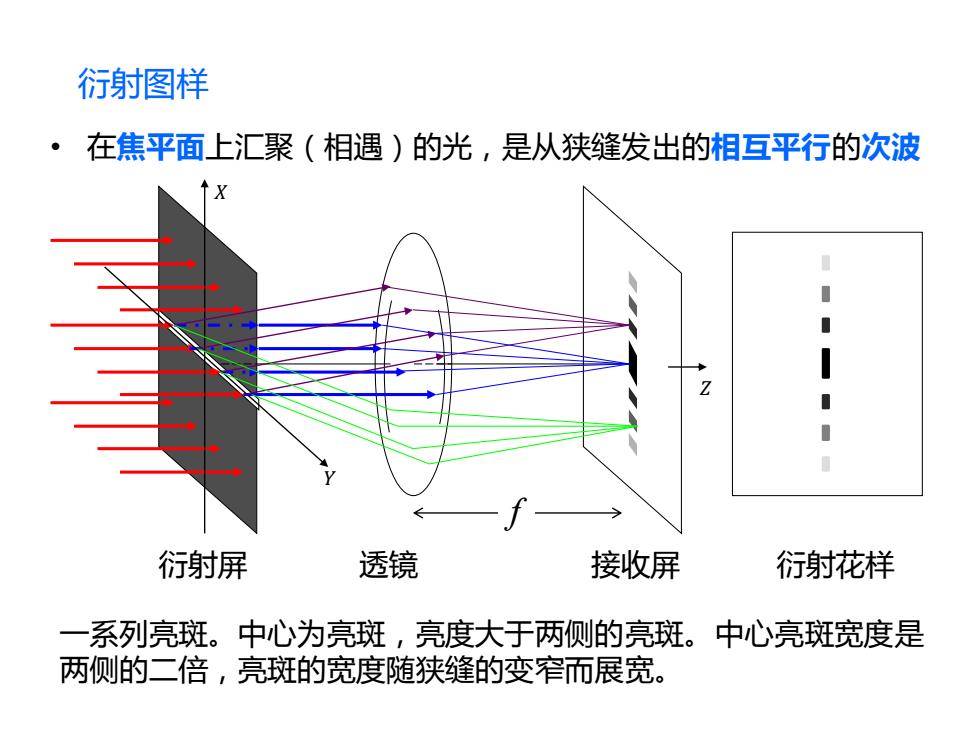
衍射图样 在焦平面上汇聚(相遇)的光,是从狭缝发出的相互平行的次波 衍射屏 透镜 接收屏 衍射花样 一系列亮斑。中心为亮斑,亮度大于两侧的亮斑。中心亮斑宽度是 两侧的二倍,亮斑的宽度随狭缝的变窄而展宽
衍射图样 • 在焦平面上汇聚(相遇)的光,是从狭缝发出的相互平行的次波 𝑋 𝑌 𝑍 衍射屏 透镜 接收屏 衍射花样 f 一系列亮斑。中心为亮斑,亮度大于两侧的亮斑。中心亮斑宽度是 两侧的二倍,亮斑的宽度随狭缝的变窄而展宽
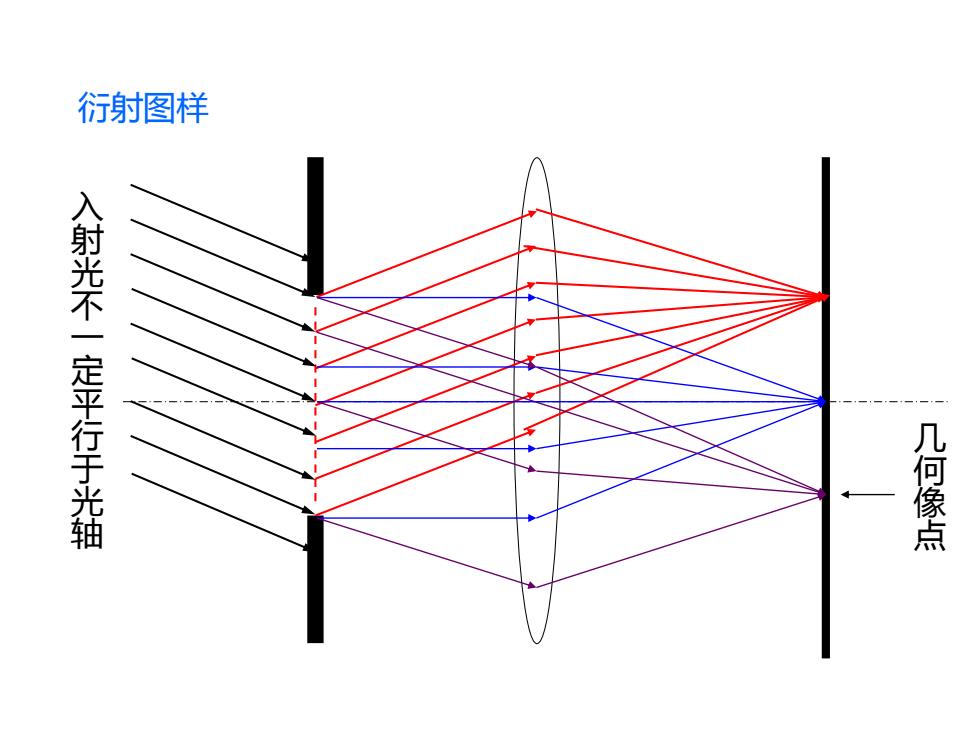
衍射图样 入射光不一定平行于光轴 几何像点
衍射图样 入射光不一定平行于光轴 几何像点
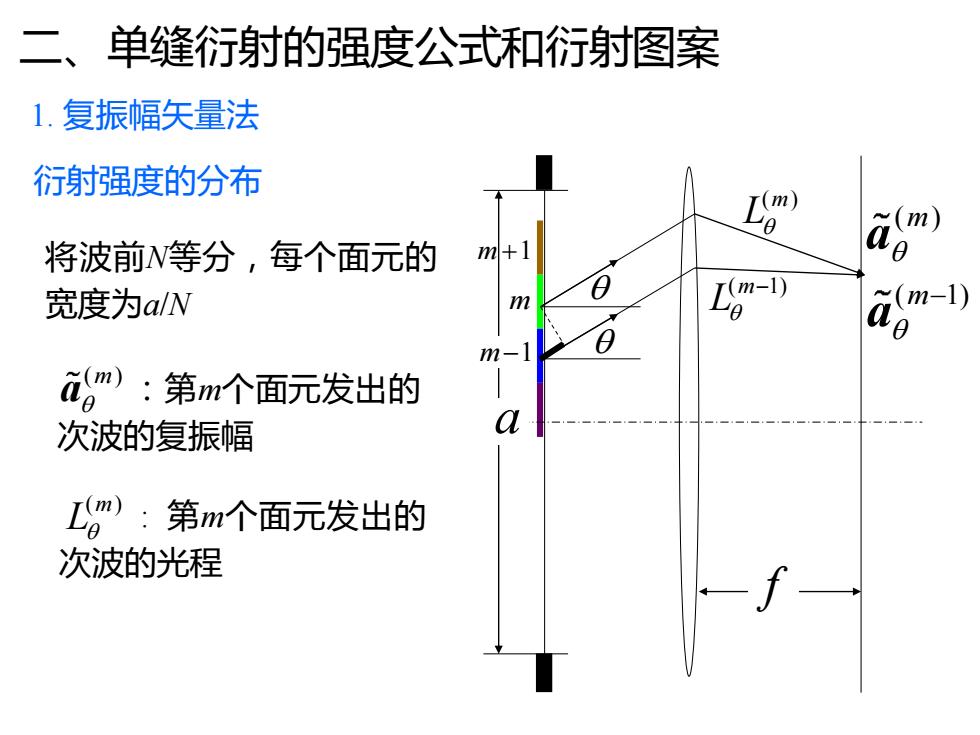
二、 单缝衍射的强度公式和衍射图案 1.复振幅矢量法 衍射强度的分布 (m 将波前W等分,每个面元的 m+1 宽度为alW m Lgm-可 (m-1) m- 论m):第m个面元发出的 次波的复振幅 a Lgm):第m个面元发出的 次波的光程
二、单缝衍射的强度公式和衍射图案 1. 复振幅矢量法 ( ) m a ( ) m L ( 1) m − a ( 1) m L − a f m m−1 衍射强度的分布 将波前N等分,每个面元的 宽度为a/N :第m个面元发出的 次波的复振幅 ( ) m a : 第m个面元发出的 次波的光程 ( ) m L m +1
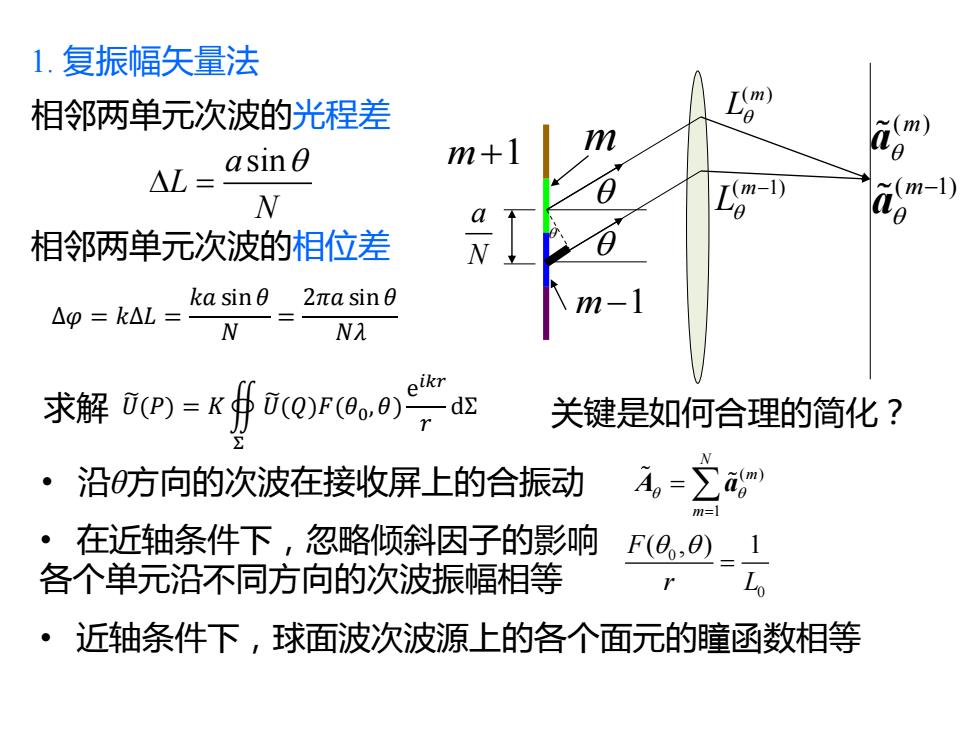
1.复振幅矢量法 相邻两单元次波的光程差 L6 m AL= asinO m+1 (m-1) N (m-1) 0 相邻两单元次波的相位差 ka sin02πasin9 △p=k△L= m-1 N Nλ 求解0=K eikr U(Q)F(0o.)d 关键是如何合理的简化? ·沿方向的次波在接收屏上的合振动 A,=2g ·在近轴条件下,忽略倾斜因子的影响 F(0,)1 各个单元沿不同方向的次波振幅相等 Lo ·近轴条件下,球面波次波源上的各个面元的瞳函数相等
1. 复振幅矢量法 m+1 ( ) m a ( ) m L m ( 1) m − a ( 1) m L − m−1 Δ𝜑 = 𝑘Δ𝐿 = 𝑘𝑎 sin 𝜃 𝑁 = 2𝜋𝑎 sin 𝜃 𝑁𝜆 相邻两单元次波的光程差 a sin L N = 相邻两单元次波的相位差 • 沿θ方向的次波在接收屏上的合振动 ( ) 1 N m m = A a = • 在近轴条件下,忽略倾斜因子的影响 各个单元沿不同方向的次波振幅相等 𝑈෩(𝑃) = 𝐾 Σ 𝑈෩(𝑄)𝐹(𝜃0,𝜃) e 𝑖𝑘𝑟 𝑟 dΣ 0 0 F( , ) 1 r L = a N • 近轴条件下,球面波次波源上的各个面元的瞳函数相等 求解 关键是如何合理的简化?
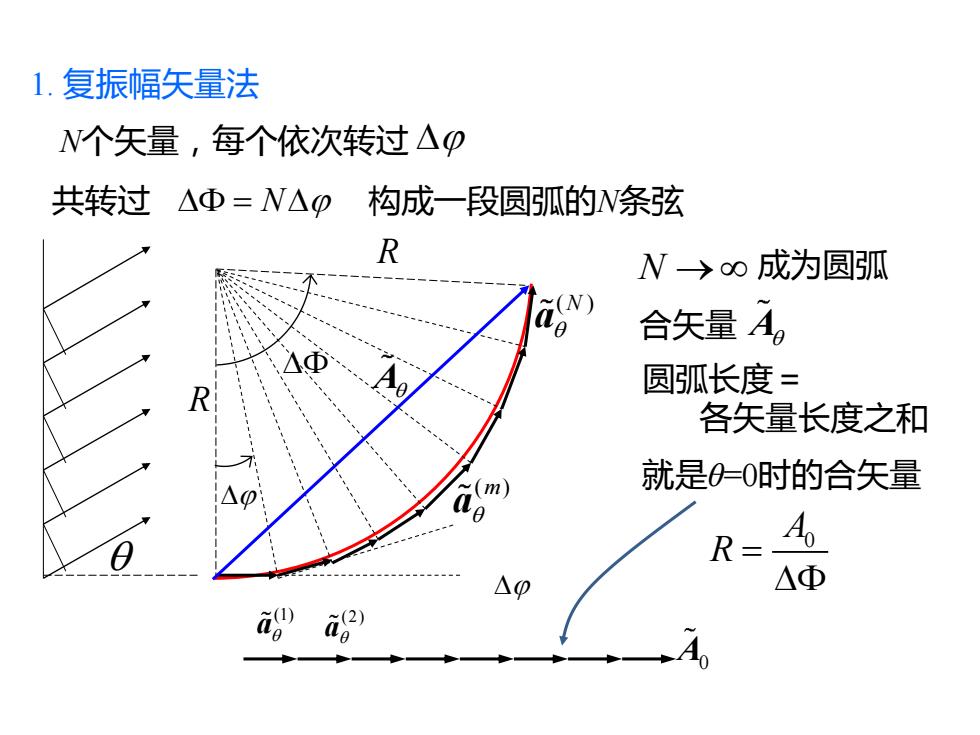
1.复振幅矢量法 N个矢量,每个依次转过△0 共转过△Φ=N△0 构成一段圆弧的条弦 R N→0成为圆弧 (N 合矢量A, 圆弧长度= 各矢量长度之和 m) 就是0=0时的合矢量 △0 R=4 △p △Φ A
1. 复振幅矢量法 ( ) N a (2) a 圆弧长度= 各矢量长度之和 (1) a ( ) m a R R N个矢量,每个依次转过 共转过 = N 构成一段圆弧的N条弦 N → 成为圆弧 合矢量 A 就是θ=0时的合矢量 A0 A0 R = A
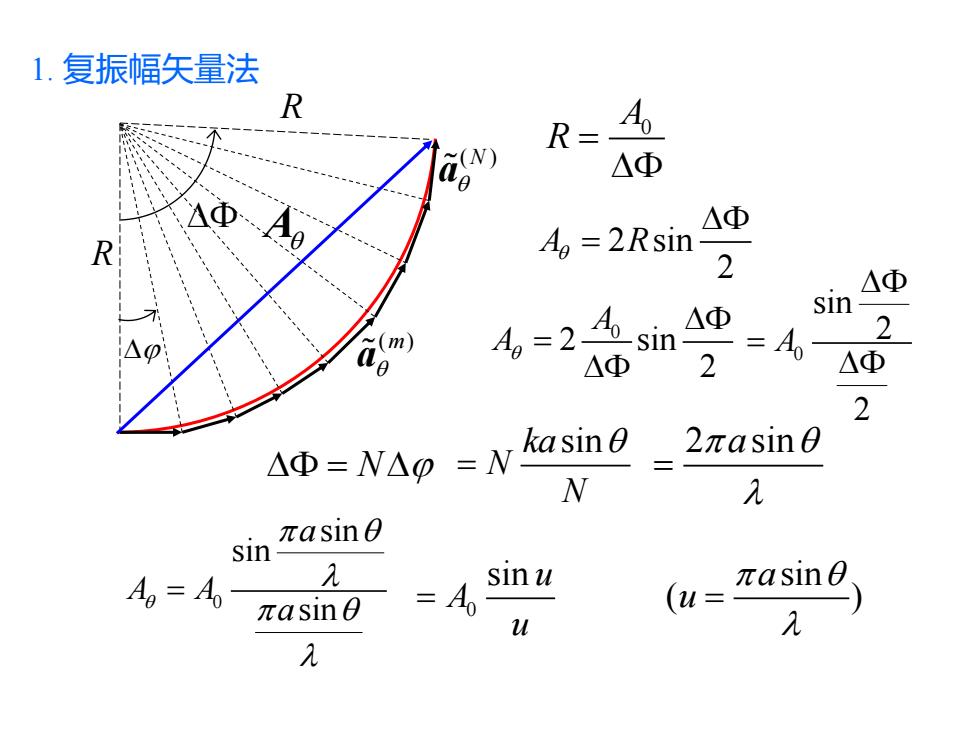
1.复振幅矢量法 R R= A △Φ △Φ A0=2Rsin 2 △Φ 4,=2n Φ sin =A 2 △Φ 2 △Φ 2 kasin02πasin0 △Φ=NAp=N N sin πasin O Ao=Ao- sin u πasinθ πasin0 =A0 (u= u 几
1. 复振幅矢量法 ( ) N a ( ) m a R R A A0 R = 2 sin 2 A R = 0 2 sin 2 A A = 0 sin 2 2 A = = N ka sin N N = 2 sin a = 0 sin sin sin a A A a = 0 sin u A u = sin ( ) a u =
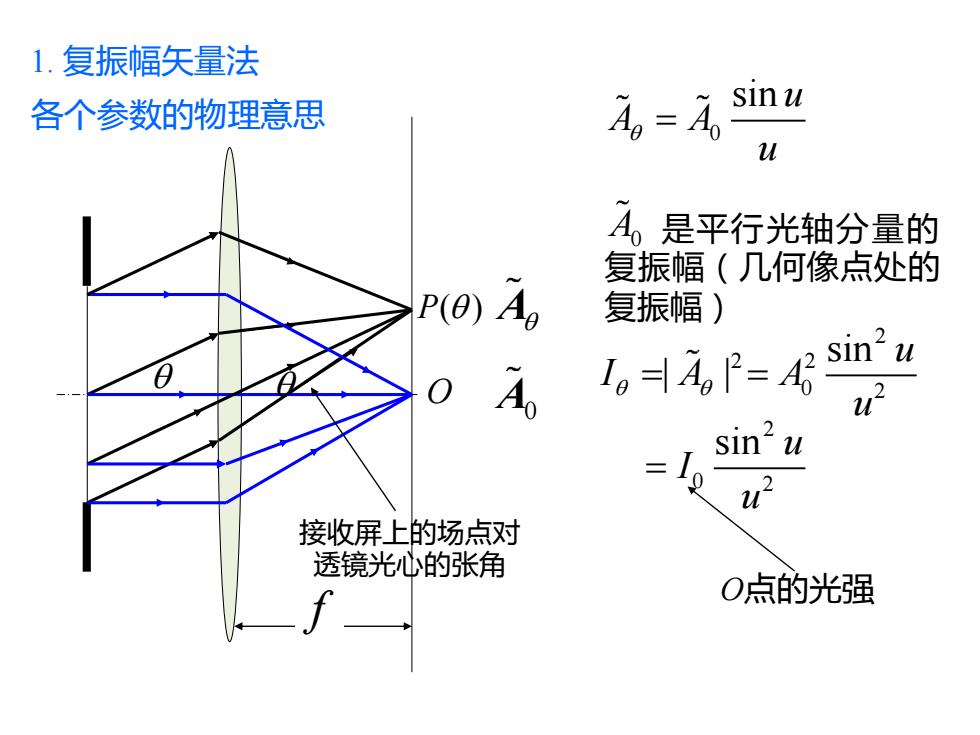
1.复振幅矢量法 各个参数的物理意思 4=A sin u Ao 是平行光轴分量的 复振幅(几何像点处的 P(0)Ao 复振幅) A 1,P=4gs1n4 sin'u 接收屏上的场点对 透镜光心的张角 O点的光强
1. 复振幅矢量法 各个参数的物理意思 P( ) O A A0 0 sin u A A u = 2 2 2 0 2 sin | | u I A A u = = 2 0 2 sin u I u = O点的光强 接收屏上的场点对 透镜光心的张角 f A0 是平行光轴分量的 复振幅(几何像点处的 复振幅)