
第4章 光的衍射 什么是衍射现象 惠更斯-菲涅耳原理 菲涅耳圆孔衍射 夫琅禾费单缝衍射与圆孔衍射 光栅
第4章 光的衍射 什么是衍射现象 惠更斯-菲涅耳原理 菲涅耳圆孔衍射 夫琅禾费单缝衍射与圆孔衍射 光栅
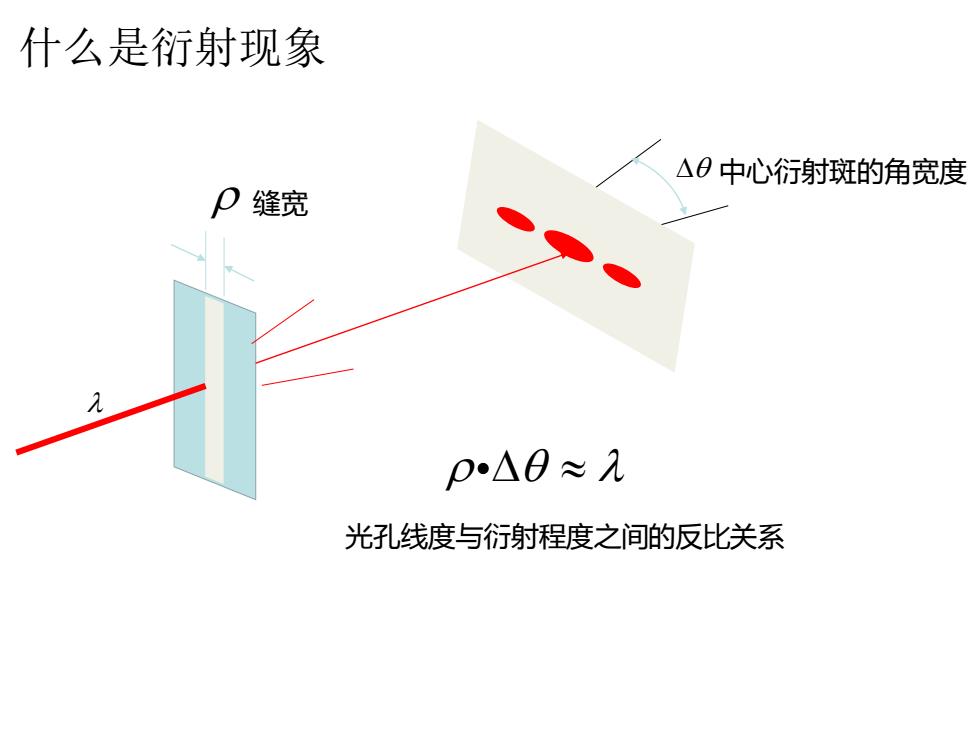
什么是衍射现象 △0中心衍射斑的角宽度 缝宽 p△0≈λ 光孔线度与衍射程度之间的反比关系
缝宽 中心衍射斑的角宽度 光孔线度与衍射程度之间的反比关系 什么是衍射现象
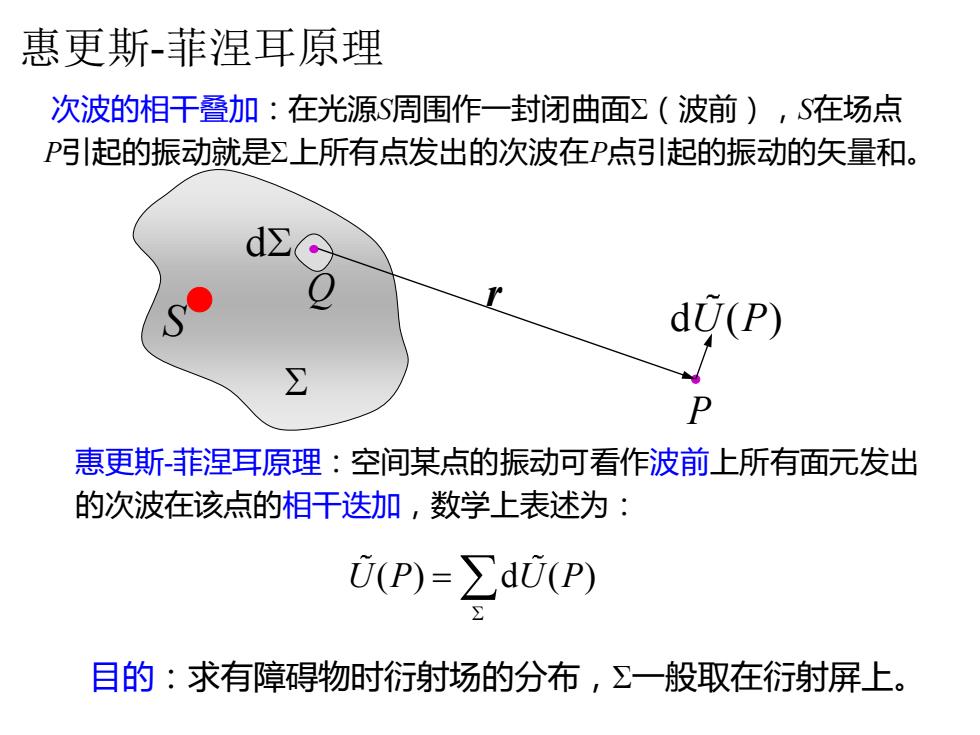
惠更斯-菲涅耳原理 次波的相干叠加:在光源S周围作一封闭曲面Σ(波前),S在场点 P引起的振动就是Σ上所有点发出的次波在P点引起的振动的矢量和。 dU(P) P 惠更斯菲涅耳原理:空间某点的振动可看作波前上所有面元发出 的次波在该点的相干迭加,数学上表述为: 0(P)=∑d0(P 目的:求有障碍物时衍射场的分布,∑一般取在衍射屏上
惠更斯-菲涅耳原理:空间某点的振动可看作波前上所有面元发出 的次波在该点的相干迭加,数学上表述为: 次波的相干叠加:在光源S周围作一封闭曲面Σ(波前),S在场点 P引起的振动就是Σ上所有点发出的次波在P点引起的振动的矢量和。 P Q d r S d ( ) U P U P U P ( ) d ( ) = 目的:求有障碍物时衍射场的分布,Σ一般取在衍射屏上。 惠更斯-菲涅耳原理
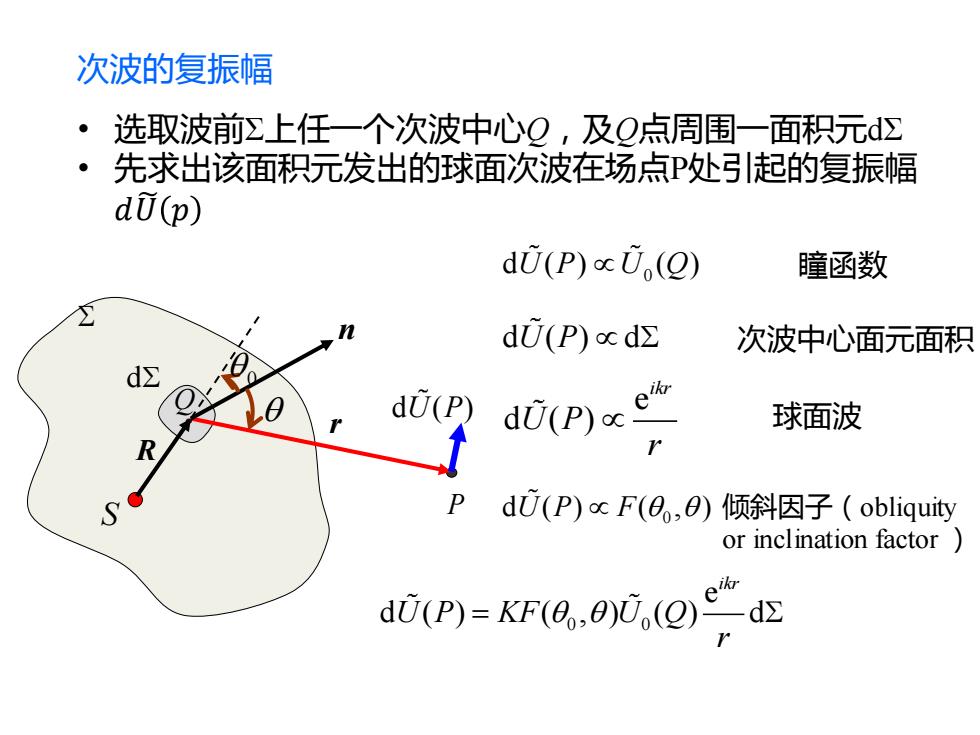
次波的复振幅 选取波前Σ上任一个次波中心Q,及Q点周围一面积元d∑ 先求出该面积元发出的球面次波在场点P处引起的复振幅 dU(p) dU(P)U(2) 瞳函数 dU(P)cd∑ 次波中心面元面积 du(P 00ag 球面波 P dU(P)cF(0,0)倾斜因子(obliquity or inclination factor e d0(P)=KF(0,0)0(Q)d∑
次波的复振幅 • 选取波前Σ上任一个次波中心Q,及Q点周围一面积元dΣ • 先求出该面积元发出的球面次波在场点P处引起的复振幅 𝑑𝑈෩ 𝑝 0 n P Q d r R d ( ) U P S 0 d ( ) ( ) U P U Q 瞳函数 d ( ) d U P 次波中心面元面积 e d ( ) ikr U P r 球面波 0 d ( ) ( , ) U P F 倾斜因子(obliquity or inclination factor ) 0 0 e d ( ) ( , ) ( ) d ikr U P KF U Q r =

惠更斯-菲涅耳衍射积分公式 ·将波前上所有次波中心发出的次波在P点的振动相干叠加,即可 得到P点的振动; ·由于次波中心在波前上连续分布,因而叠加(求和)的过程就 变为求积分的过程,得到惠更斯-菲涅耳衍射积分公式。 f.d0P)-∯KT(ao0,Qdy 其中:(Q)为波前上面元的复振幅
惠更斯-菲涅耳衍射积分公式 • 将波前上所有次波中心发出的次波在P点的振动相干叠加,即可 得到P点的振动; • 由于次波中心在波前上连续分布,因而叠加(求和)的过程就 变为求积分的过程,得到惠更斯-菲涅耳衍射积分公式。 0 0 e d ( ) ( , ) ( ) d ikr U P KF U Q r = 其中: 𝑈෪0 𝑄 为波前上面元的复振幅
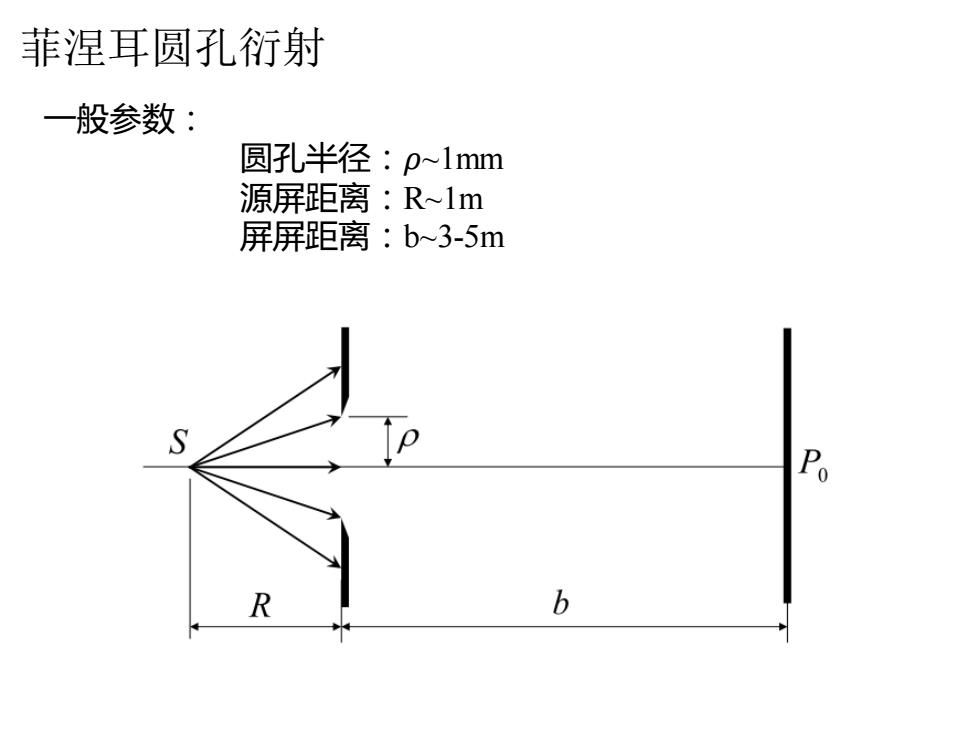
菲涅耳圆孔衍射 一般参数: 圆孔半径:p~lmm 源屏距离:R~lm 屏屏距离:b~3-5m P。 R b
菲涅耳圆孔衍射 一般参数: 圆孔半径:𝜌~1mm 源屏距离:R~1m 屏屏距离:b~3-5m
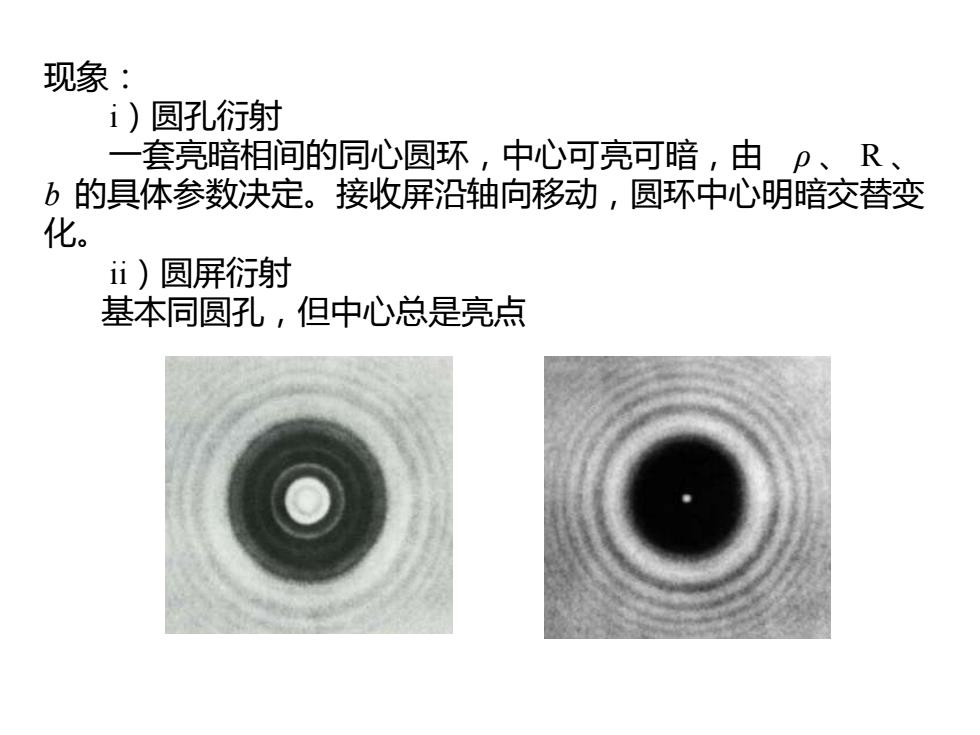
现象: ⅰ)圆孔衍射 一 套亮暗相间的同心圆环,中心可亮可暗,由p、R、 b的具体参数决定。接收屏沿轴向移动,圆环中心明暗交替变 化。 iⅱ)圆屏衍射 基本同圆孔,但中心总是亮点
现象: i)圆孔衍射 一套亮暗相间的同心圆环,中心可亮可暗,由 ρ 、 R 、 b 的具体参数决定。接收屏沿轴向移动,圆环中心明暗交替变 化。 ii)圆屏衍射 基本同圆孔,但中心总是亮点

重点!!!夫琅禾费单缝衍射 实验装置 衍射屏 观察屏 镜 镜 ·平行光入射,用凸透镜成像于像方焦平面。 ·相当于各点发出的次波汇聚于无穷远处。即是平行光的相 干叠加
• 平行光入射,用凸透镜成像于像方焦平面。 • 相当于各点发出的次波汇聚于无穷远处。即是平行光的相 干叠加。 实验装置 重点!!!夫琅禾费单缝衍射
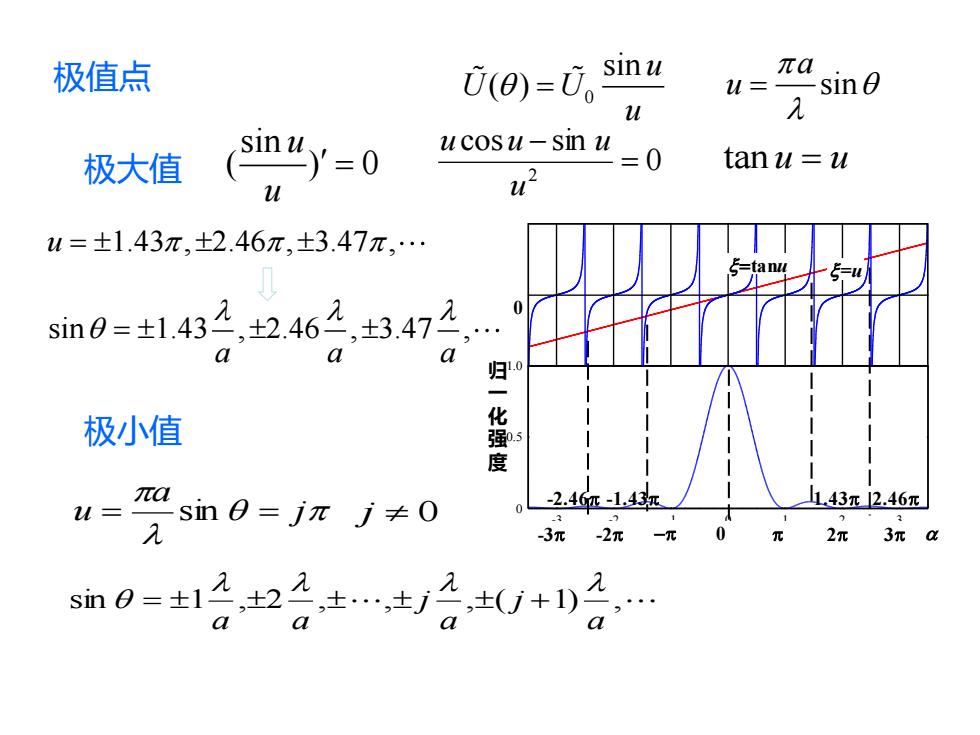
极值点 0(0)=0, sinu πa u=-sin0 u λ (sinu=0 ucosu-sin u 极大值 .0 tan uu u=±1.43m,±2.46π,±3.47π,. 5tan叫 sim0=±1.432,±2462,士3472 0 a 归0 极小值 度 sm0=jnJ≠0 u= πa -2.46匹-1.43红 143元2.46元 -3元-2π -元0元 2元3元a a
极值点 0 cos sin 2 = − u u u u tan u u = sin 1.43 , 2.46 , 3.47 , a a a = 极大值 sin ( ) 0 u u = 0 0.5 1.0 -3 -2 -1 0 1 2 3 -2.46p -1.43p 1.43p 2.46p -3p -2p −p 0 p 2p 3p x=tanu x=u 0 归 一 化 强 度 a sin a u p = 极小值 0 sin ( ) u U U u = p p j a u = sin = j 0 sin 1 , 2 , , , ( 1) , a j a j a a = + u = 1.43 , 2.46 , 3.47 , p p p
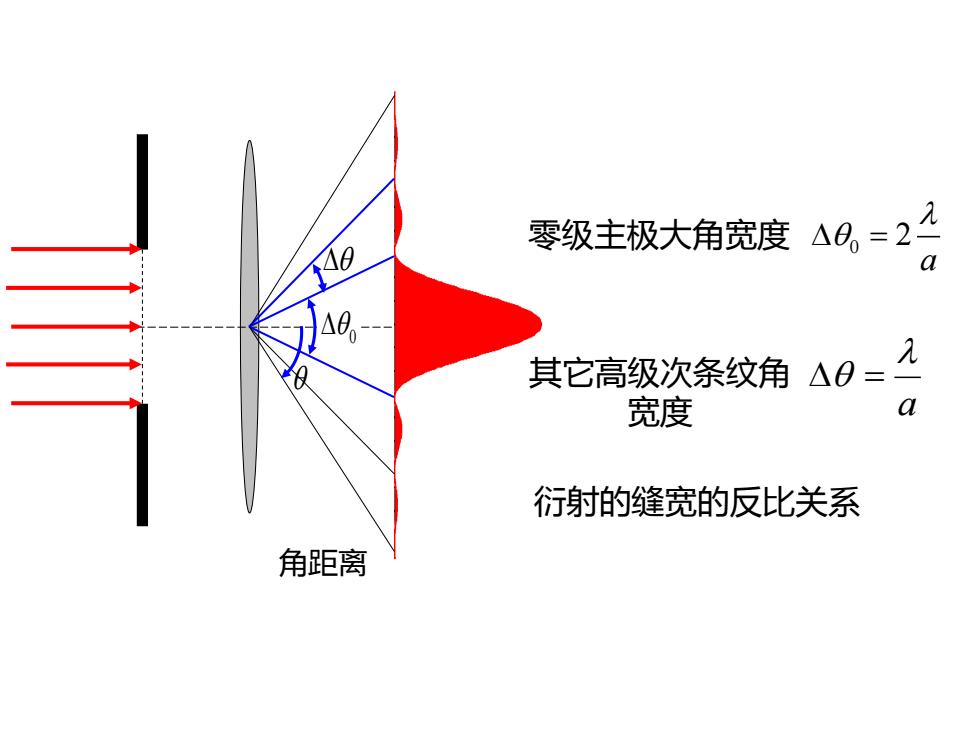
零级主极大角宽度48,=2 a 其它高级次条纹角△0= 宽度 a 衍射的缝宽的反比关系 角距离
0 0 2 a 零级主极大角宽度 = 其它高级次条纹角 宽度 a = 衍射的缝宽的反比关系 角距离