2.电子导电:金属 这样的模型实际上类似量子 力学中的“一维无限深方势 阱” 2 nπx p(x)= n2π2h2 En=2mL2 =1 但是由此引出一个问题: 这样一来,波函数是以材料表面为边界的“驻波”,而“行波”才能 更好的研究电子传输行为 "God made the bulk,the surface was invented by the devil." Wolfgang Pauli
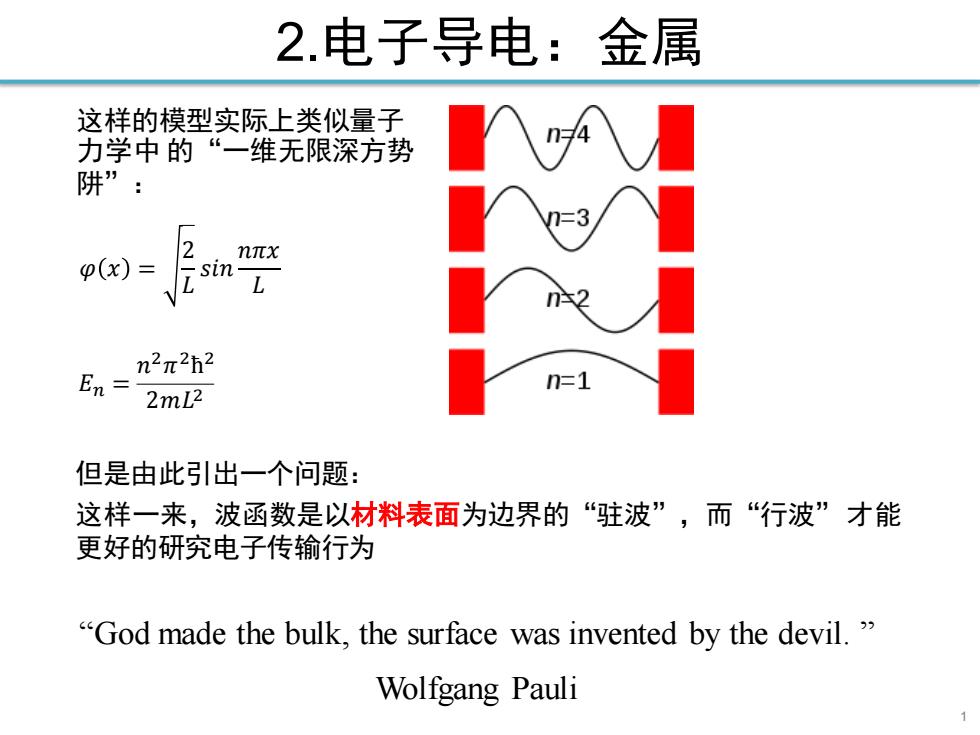
1 2.电子导电:金属 这样的模型实际上类似量子 力学中 的“一维无限深方势 阱”: 𝜑 𝑥 = 2 𝐿 𝑠𝑖𝑛 𝑛𝜋𝑥 𝐿 𝐸𝑛 = 𝑛 2𝜋 2ħ 2 2𝑚𝐿 2 但是由此引出一个问题: 这样一来,波函数是以材料表面为边界的“驻波”,而“行波”才能 更好的研究电子传输行为 “God made the bulk, the surface was invented by the devil. ” Wolfgang Pauli

2.电子导电:金属 Sommerfield模型中回避表面问题的方式:“起点即终点” 0(化,乃+L)=p化,)
2 2.电子导电:金属 Sommerfield模型中回避表面问题的方式:“起点即终点” 对于一维空间,相当于让直线闭合成圆环: 表面 材料内部 表面 L 周长L 表面重合 边界条件: x [0, L]时(x) = 0 (x+L) = (x) 将这一边界条件拓展到三维空间,就是所谓的Born-von Karman条件 (x+L, y, z) = (x, y, z) (x, y+L, z) = (x, y, z) (x, y, z+L) = (x, y, z)

2.电子导电:金属 h2 72φ()=Ep() 2m 通过代入法可以验证,薛定谔方程的解(无论是否考虑边界条件) 和对应的能量E具备以下形式: pk()= 4= 2m 其中是一个量子化的矢量,可以被理解为代表电子的物质波的波矢 因此,根据动量、能量、波长间的关系,容易得出k和波长入以及动量 有以下关系 市=hk 2π
3 2.电子导电:金属 − ħ 2 2𝑚 𝛻 2 𝑟 Ԧ = 𝐸 𝑟 Ԧ 通过代入法可以验证,薛定谔方程的解(无论是否考虑边界条件) 和对应的能量E具备以下形式: 𝜑𝑘 𝑟 Ԧ = 1 𝑉 𝑒 𝑖𝑘∙𝑟Ԧ 𝐸𝑘 = ħ 2 𝑘 2 2𝑚 其中𝑘是一个量子化的矢量,可以被理解为代表电子的物质波的波矢 因此,根据动量、能量、波长间的关系,容易得出𝑘和波长 以及动量p 有以下关系 = 2𝜋 𝑘 𝑝 Ԧ = ħ𝑘

2.电子导电:金属 由于薛定谔方程的解pk()需要服从Born-von Karman条件: p(x+L,y.z=p(x,y.2) 0(x,y+L,2)=p(x,y2) o(x,y,z+L=(x,y2 将p()=eif代入以上三个边界条件后,很容易得到 eikxl =eikyl eikzl =1 (kk,k为k在x,y方向上的分量) nx,n,n可以取任意整数
4 2.电子导电:金属 由于薛定谔方程的解𝜑𝑘 𝑟 Ԧ 需要服从Born-von Karman条件: (x+L, y, z) = (x, y, z) (x, y+L, z) = (x, y, z) (x, y, z+L) = (x, y, z) 将𝜑𝑘 𝑟 Ԧ = 1 𝑉 𝑒 𝑖𝑘∙𝑟Ԧ代入以上三个边界条件后,很容易得到 𝑒 𝑖𝑘𝑥𝐿 = 𝑒 𝑖𝑘𝑦𝐿 = 𝑒 𝑖𝑘𝑧𝐿 = 1 (kx , ky , kz为𝑘在x, y, z方向上的分量) 𝑘𝑥 = 2𝜋𝑛𝑥 𝐿 , 𝑘𝑦 = 2𝜋𝑛𝑦 𝐿 , 𝑘𝑧 = 2𝜋𝑛𝑧 𝐿 nx , ny , nz可以取任意整数

2.电子导电:金属 波矢分布密度(描述k空间中单位体积包含的状态数) 在波矢量飞,飞,飞,构成的空间(k空间,动量空间)中每一个点 表示一个(n,n,n),代表一个状态。每个状态占据的体积为(2πL)3。 k空间单位体积所含点数: (2πL)3=18元=p 由于每个波矢可以容纳自旋相反的两个电子,在体积元d之中可容 纳的电子状态数为 dZ 2p(k)dk dk ky 二维: 三维: 每个点对应一个电子 k空间中电子 k波失,每个波失占据 态所对应的等 k空间(2π/L)2的面积, 能面为球形。 以原点为圆心的圆形 上每一点能量相同
5 2.电子导电:金属 波矢分布密度(描述k空间中单位体积包含的状态数) 二维: 每个点对应一个电子 波失,每个波失占据 k 空间(2π/L)2的面积, 以原点为圆心的圆形 上每一点能量相同。 三维: k空间中电子 态所对应的等 能面为球形。 状态数为

2.电子导电:金属 电子的能级密度(描述单位能量范围内容纳的电子数) 如果以NE)表示能量低于或等于E的电子态的数量 那么Z(E)=dWdE-能级E的态密度(Density of States,DOS) 波矢k的电子能量为E(k)= k2 2m 2m 在能量为E的球体中,波矢k的取值总数为 N=2p(k)3ks p=/8π3 k=√2mE/方 态密度Z(E)为 PDOS gl/2 Z(E)=dN/dE C√E C= V(2m 3/2 PDOS 2m2方2 E=const. 不同维度DOS与E关系 3D:E12 2D:常数 DOS 1D:~E1/2 x6-1/2 E
𝑁 = 2𝜌(𝒌) 4 3 𝜋𝒌 3 6 2.电子导电:金属 电子的能级密度(描述单位能量范围内容纳的电子数) 如果以N(E) 表示能量低于或等于E的电子态的数量 那么Z(E) = dN/dE = 能级E的态密度(Density of States, DOS)

2.电子导电:金属 根据Pui不相容原理,每个量子态(即每个)只能被两个自旋相反的电 子占据。 因此,在基态(T=0K),电子结构可以这样确定:将电子逐个填入未被 占据的能量最低的电子态中,直到N个电子都“各得其所”。 如果N足够大,那么被占据的轨道在k空间中看来将接近一个球形。它的球 面称为费米面,其半径称为费米波矢kF,能量称为费米能量E,Ek称为 费米温度T 关于费米能量E更严格的定义: 费米面 0K时金属基态系统电子所占有的能 级最高的能量
7 2.电子导电:金属 根据Pauli不相容原理,每个量子态(即每个𝑘)只能被两个自旋相反的电 子占据。 因此,在基态(T = 0 K),电子结构可以这样确定:将电子逐个填入未被 占据的能量最低的电子态中,直到N个电子都“各得其所”。 如果N足够大,那么被占据的轨道在k空间中看来将接近一个球形。它的球 面称为费米面,其半径称为费米波矢𝑘𝐹,能量称为费米能量EF,EF /kB称为 费米温度TF。 关于费米能量EF更严格的定义: 0K时金属基态系统电子所占有的能 级最高的能量 费米面
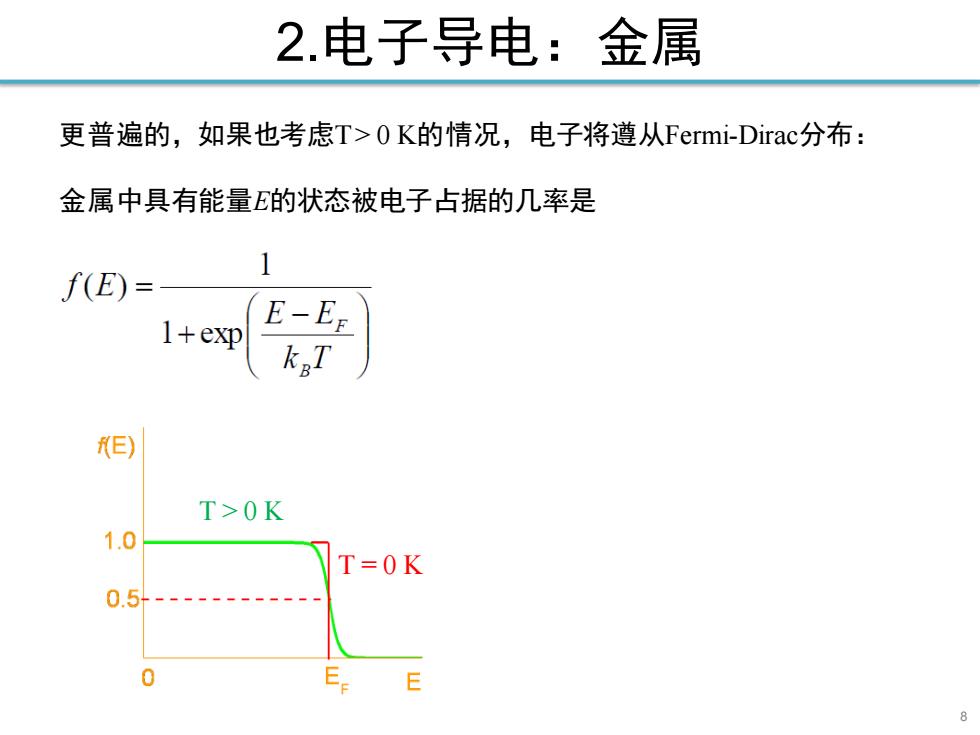
2.电子导电:金属 更普遍的,如果也考虑T>OK的情况,电子将遵从Fermi-Dirac分布: 金属中具有能量E的状态被电子占据的几率是 f(E)= 1+exp E-Er E) T>OK 1.0 T=0K 0.5- 0 E E
8 2.电子导电:金属 更普遍的,如果也考虑T > 0 K的情况,电子将遵从Fermi-Dirac分布: 金属中具有能量E的状态被电子占据的几率是 T > 0 K T = 0 K

2.电子导电:金属 Sommerfield模型的成功之处 因为不考虑电子间相互作用,金属内能即为所有电子能量之和 U=2EfE) 6 cal/mol."C 根据比热容的定义G,=(别), 可以算出Cv=k()xT 比Drude模型更好的解释了电子 室 对比热容的贡献 Sommerfield模型的缺陷 假设过于简单,并未考虑原子核的周期性排列所形成的周期性势能
9 2.电子导电:金属 因为不考虑电子间相互作用,金属内能即为所有电子能量之和 𝑈 = 2 𝑘 𝐸𝑘𝑓(𝐸𝑘) 根据比热容的定义𝐶𝑉 = 1 𝑉 𝜕𝑈 𝜕𝑇 𝑉 可以算出𝐶𝑉 = 𝜋 2 2 𝑁 𝑉 𝑘𝐵 𝑇 𝑇𝐹 𝑇 比Drude模型更好的解释了电子 对比热容的贡献 Sommerfield模型的成功之处 Sommerfield模型的缺陷 假设过于简单,并未考虑原子核的周期性排列所形成的周期性势能

2.电子导电:金属 金属导电 经典自由电子论 理论研究 的发展: 1900年德鲁特 量子力学基础 量子自由电子论 能带论 1927年索末菲 1928年Bloch 保持自由电子观点, 1931年Wilson 用量子行为约束。 简单直观, 使用方便。 彻底改变观念,放弃自由假定, 建立了固体理论新模式。 理论复杂数十年发展方才完善
10 2.电子导电:金属