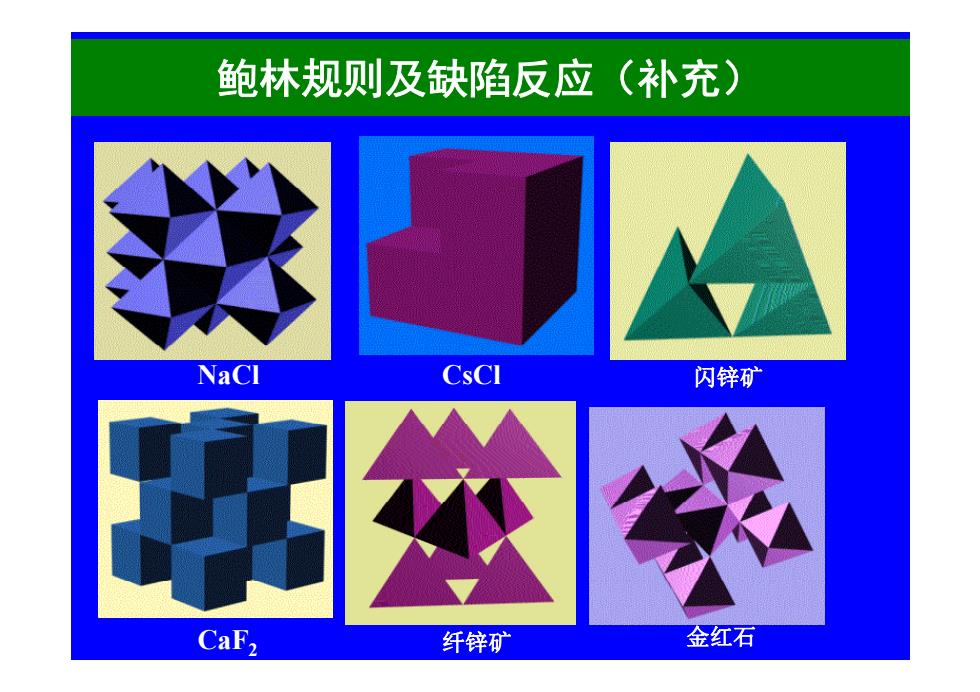
鲍林规则及缺陷反应(补充) NaCl 闪锌矿 CaF, 纤锌矿 金红石
鲍林规则及缺陷反应(补充) NaCl CsCl 闪锌矿 CaF 2 纤锌矿 金红石

Electrostatic Bond Valence Principle Pauling第二规则(电价规则):设Z为正离 子带的电荷数,u为其配位数,从正离子到每一个 配位负离子间的静电键强度$定义为: Bond valence;bond strength 或者,在一个稳定的离子型结构中,负离子的 电价等于或近乎等于从邻近的正离子至该负离子各 静电键强度之总和:即 实际上,该规则对正离子的电价也成立: Z=∑S,=∑
Electrostatic Bond Valence Principle Pauling 第二规则(电价规则):设Z +为正离 子带的电荷数,u为其配位数 从正离子到每 个 为其配位数 ,从正离子到每 一 个 配位负离子间的静电键强度 S定义为: Z S 配位负离子间的静电键强度 S定义为: u S 或者,在 一个稳定的离子型结构中,负离子的 Bond valence; bond strength 或者,在 个稳定的离子型结构中,负离子的 电价等于或近乎等于从邻近的正离子至该负离子各 静电键强度之总和:即 i i i i i u Z Z S i i ui 实际上,该规则对正离子的电价也成立: Z i i i i i u Z Z S

Z为负离子电荷数(电价),S指某一负离子 至每一个以负离子为顶点的多面体中央的正离子的 静电键强度(electrostatic bond strength,.ebs),这就是 电价规则。 Example1:NaC1,其静电键强度为 6 则C1的电价 乙a=∑s,=6×61 上下、前后、左右共6个八面体共用一个C1 顶点
Z -为负离子电荷数(电价),Si指某一负离子 至每 个以负离子为顶点的多面体中央的正离子的 至每一个以负离子为顶点的多面体中央的正离子的 静电键强度(electrostatic bond strength, (electrostatic bond strength, ebs),这就是 电价规则。 Example 1 NaCl 其静电键强度为 1 Example 1:NaCl,其静电键强度为 S 则Cl-的电价 6 S i 1 1 则Cl 的电价 Z S i 6 上下、前后、左右共6个八面体共用一个Cl- 顶点 1 6 6 i Z Cl S i 顶点
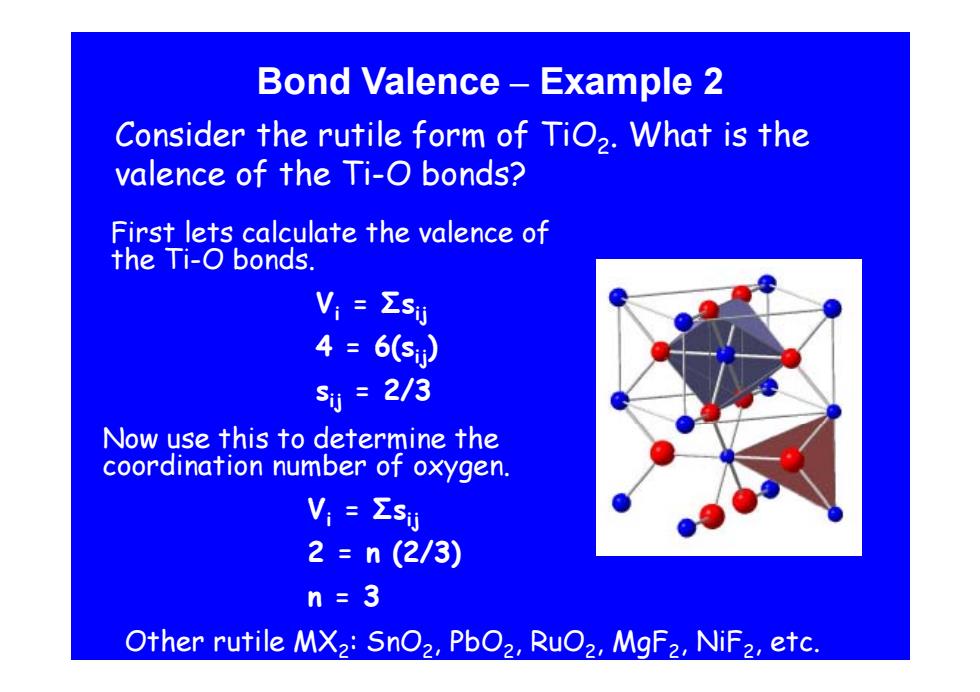
Bond Valence -Example 2 Consider the rutile form of TiO2.What is the valence of the Ti-O bonds? First lets calculate the valence of the Ti-O bonds. V,=Σsy 4=6(5) s1=2/3 Now use this to determine the coordination number of oxygen. Vi Esij 2=n(2/3) n=3 Other rutile MX2:SnO2,PbO2,RuO2,MgF2,NiF2,etc
Bond Valence – Example 2 Consider the rutile form of TiO2. What is the valence of the Ti-O bonds? First lets calculate the valence of the Ti-O bonds. O bonds. Vi = Σsij 4 = 6(s 4 = 6(s )ij sij = 2/3 Now use this to determine the coordination number of oxygen. Vi = Σsij 2 = n (2/3) n = 3 Other rutile MX2: SnO2, PbO2, RuO2, MgF2, NiF2, etc

Bond Valence-Example 3 What is the oxygen coordination in the mineral zircon(锆石,锆英石),Zrsio4,where Si"4is tetrahedrally coordinated and Zr+4 is eight coordinated? First lets calculate the valence of the Si-O bonds. V,=Σsj 4=455i-o) S5i-0=1
Bond Valence Bond Valence – Example 3 Example 3 What is the oxygen coordination in the mineral zircon(锆石,锆英石) ZrSiO4 where Si+4 zircon(锆石,锆英石), ZrSiO is 4, where Si is tetrahedrally coordinated and Zr+4 is eight coordinated? First lets calculate the valence of the Si valence of the Si-O bonds. O bonds. Vi = Σsij 4 = 4(sSi-O) sSi-O = 1

Now lets calculate the valence of the Zr-O bonds. V,=ΣsU 4=8(szr-o) Szr-0=1/2 Now lets calculate the coordination number of oxygen. Vi n1 Ssi-o n2 Szr-0 2=n1(1)+n2(1/2) n1=1n2=2 立方体 十二面体 Figure 9.4 Distortion of a cubic arrangement of ligands togive the dodecahedral structure
Now lets calculate the valence of th Ze Zr-O b nds O b onds. Vi = Σ sij 4 = 8 (sZr-O ) sZr-O = 1/2 N l ll h Now lets calculate t he coordination number of oxygen. Vi = n 1 sSi-O + n 2 sZr-O 2 = n (1) (1/2) 1 + n 2 (1/2) n 1 =1 n 2 = 2 立方体 十二面体

A new Li-ionic conductor:LiOCl OCIoLi 求锂离子周围的阴离子 配位? VLi n1 SLi-o n2 SLi-a (b) 1=n1(1/3)+n2(1/12) (a) (c) 12=4n1+n2 Fig.1 (a)The crystal structures of LigOCl with LiO octahedron,(b)LiCl cuboctahedron,and (c) coordination environments.The cube enclosed by solid black lines denotes a unitcell The small purple balls denote Li ions,while the medium sized red and big sized green balls are Oions and Clions,respectively.All Li,and Clatoms are represented with the spheres of the same color and size in the following of this paper. Hence,nj=2 n2=4 An antiperovskite structure:LiO,LiCl,LiO2Cla J.Mater.Chem.A,2018,6,1150
A new Li-ionic conductor: Li 3OCl 求锂离子周围的阴离子 配位? VLi = n 1 sLi-O + n 2 sLi-Cl 1 = n 1 (1/3) + n 2 (1/12) 12 = 4 n 1 + n 2 A i ki i O i Cl iO Cl Hence, n 1=2 n 2=4 An ant iperovskite structure: L i 6 O, L i12Cl, LiO 2Cl 4 J. Mater. Chem. A, 2018,6, 1150

§Pauling第二规则的发展和应用 -定量键价方法(Quantitative Bond Valence Method) West,p.231 Bond valence 20 75 39 Na,O (反萤石结构) Bond length (A) 氧与第二周期原子Na,Mg,AL,Si,P,S之间的键价-键长关系(I.D Brown,.1978)[O-M键长:1.43(S0),1.60,1.62(SiO22.65Na2O] Sy=(Ro/R)N P,Os ·式中R是键长,R,、N为常数(R,是单位键价的键长值) ◆对上图代表的元素,R=1.622,N=4.290
§ Pauling Pauling第二规则的发展和应用 第二规则的发展和应用 -定量键价方法 (Quantitative Bond Valence Method) West, p.231 价 Q N O 氧与第二周期原子Na, Mg, Al, Si, P, S之间的键价-键长关系(I.D. Na2O (反萤石结构) N (R / R) Brown, 1978)[O-M键长:1.43(SO2); 1.60,1.62(SiO2); 2.65(Na2O)] N sij (R / R) 0 式中R是键长 R N为常数(R 是单位键价的键长值) P2O5 式中R是键长,R0、N为常数(R0是单位键价的键长值); 对上图代表的元素,R0=1.622, N=4.290

A powerful advance on Pauling's bond valence method is to guantitatively link the bond valence to the bond distance (rather than the oxidation state).While a number of scientists have helped in this endeavor the principle driving force has largely been I.D.Brown from McMaster University.1.2 The bond valence is calculated using the following relationship: si exp [(Rij dj)/b] R、dinA) Where d is the distance between atoms i and j,Ri is the empirically determined distance for a given cation-anion pair,and b is also an empirical value generally set equal to 0.37.Values of Rj that give bond valence sums near the oxidation state have been tabulated.3,4.5 1. I.D.Brown,Chem.Soc.Reviews 7,359-376(1978). 2.I.D.Brown,"The chemical bond in inorganic chemistry:the bond valence model"Oxford Univ.Press,New york(2002). 3 Brown Altermatt,Acta Cryst.B41,244-247 (1985). 4. Brese O'Keeffe,Acta Cryst.B47,192-197(1991). 5. O'Keeffe.Acta Cryst.A 46.138-142(1990)
A powerful advance on Pauling’s bond valence method is to quantitatively link the bond valence to the bond distance quantitatively link the bond valence to the bond distance (rather than the oxidation state). While a number of scientists have helped in this endeavor the principle driving force has largely been I.D. Brown from McMaster University. 1,2 The bond valence is calculated using the following relationship: following relationship: sij = exp [(Rij - dij)/b] (Rij 、 dij in Å) Where dij is the distance between atoms i and j, Rij is the empirically determined distance for a given cation-anion pair, and b is als an empirical value enerally set equal t b is also an empirical value generally set equal to 0 37 . . Values f Values o f Rij that give bond valence sums near the oxidation state have been tabulated.3,4,5
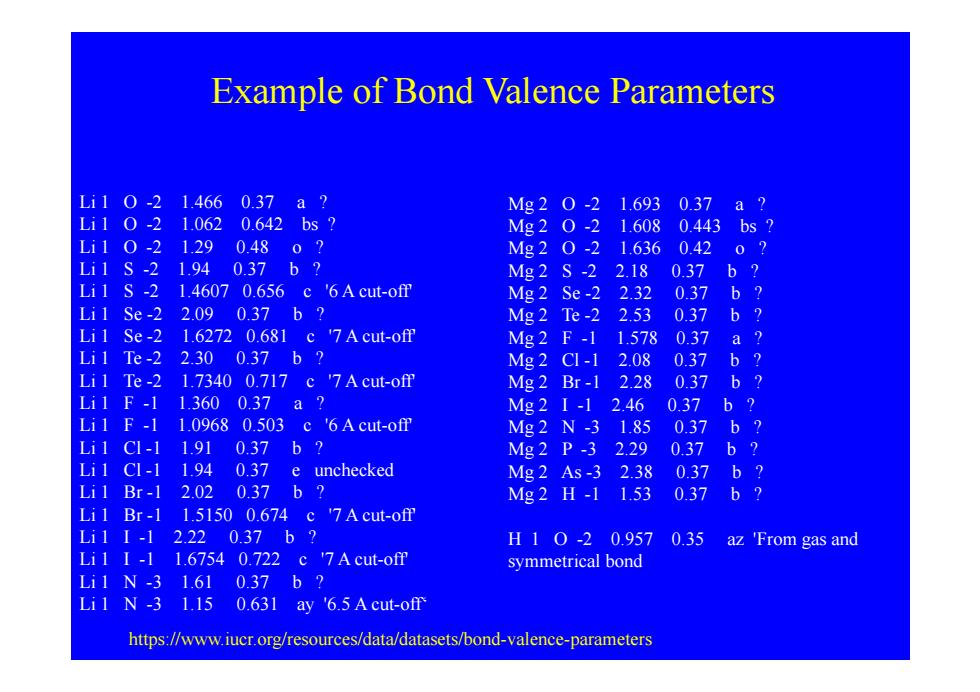
Example of Bond Valence Parameters Li10-21.4660.37a? Mg20-21.6930.37a? Li10-21.0620.642bs? Mg20-21.6080.443bs2 Li10-21.290.480? Mg20-21.6360.420? Li1S-21.940.37b? Mg2S-22.180.37b? Li1 S-2 1.4607 0.656 c '6A cut-off Mg2Se-22.320.37b? Li1Se-22.090.37b? Mg2Te-22.530.37b? Li1 Se-2 1.6272 0.681 c '7A cut-off Mg2F-11.5780.37a? Li1Te-22.300.37b? Mg2CI-12.08 0.37b? Li1 Te-2 1.7340 0.717 c '7A cut-off Mg2Br-12.280.37b? Li1F-11.3600.37a? Mg21-12.460.37b? Li1 F-1 1.0968 0.503 c '6A cut-off Mg2N-31.850.37b? Li1C1-11.91037b? Mg2P-32.29 0.37b? Li1 CI-1 1.94 0.37 e unchecked Mg2As-32.38 0.37b? Li1Br-12.020.37b? Mg2H-11.53 0.37 b? Li1 Br-1 1.5150 0.674 c '7A cut-off Lil I-1 2.220.37b? H10-20.957 0.35 az 'From gas and Li11-11.67540.722c7Acut-ofm symmetrical bond Li1N-31.610.37b? Li1 N-3 1.15 0.631 ay '6.5 Acut-off https://www.iucr.org/resources/data/datasets/bond-valence-parameters
Example of Bond Valence Parameters Li 1 O -2 1.466 0.37 a ? Li 1 O -2 1.062 0.642 bs ? Li 1 O -2 1.29 0.48 o ? Li 1 S 2 1 94 0 37 b ? Mg 2 O -2 1.693 0.37 a ? Mg 2 O -2 1.608 0.443 bs ? Mg 2 O -2 1.636 0.42 o ? Li 1 S -2 1.94 0.37 b ? M2S 2 2 18 0 37 b ? Li 1 S -2 1.4607 0.656 c '6 A cut-off' Li 1 Se -2 2.09 0.37 b ? Li 1 Se -2 1.6272 0.681 c '7 A cut-off' Mg 2 S -2 2.18 0.37 b ? Mg 2 Se -2 2.32 0.37 b ? Mg 2 Te -2 2.53 0.37 b ? Mg 2 F -1 1.578 0.37 a ? Li 1 Te -2 2.30 0.37 b ? Li 1 Te -2 1.7340 0.717 c '7 A cut-off' Li 1 F -1 1.360 0.37 a ? Li 1 F 1 1 0968 0 503 c '6 A cut off' g Mg 2 Cl -1 2.08 0.37 b ? Mg 2 Br -1 2.28 0.37 b ? Mg 2 I -1 2.46 0.37 b ? Li 1 F -1 1.0968 0.503 c 6 A cut-off M2N 3 1 85 0 37 b ? Li 1 Cl -1 1.91 0.37 b ? Li 1 Cl -1 1.94 0.37 e unchecked Li 1 Br -1 2.02 0.37 b ? Mg 2 N -3 1.85 0.37 b ? Mg 2 P -3 2.29 0.37 b ? Mg 2 As -3 2.38 0.37 b ? Mg 2 H -1 1.53 0.37 b ? Li 1 Br -1 1.5150 0.674 c '7 A cut-off' Li 1 I -1 2.22 0.37 b ? Li 1 I -1 1.6754 0.722 c '7 A cut-off' Li 1 N 3 1 61 0 37 b ? g H 1 O -2 0.957 0.35 az 'From gas and symmetrical bond Li 1 N -3 1.61 0.37 b ? Li 1 N -3 1.15 0.631 ay '6.5 A cut-off‘ https://www.iucr.org/resources/data/datasets/bond-valence-parameters