
三元相图 1
!"#$ 1

三元体系 f=C-Φ+2 共存的相数最多5相, C=3 最大自由度=4 Φmax=5-f=5 相数Φ 1 2 3 4 5 自由度 4 3 2 1 0 体系类型 四变度 三 双 单 无变度 1.完全决定一个三元体系的状态需四个参变数(T,P,C1, C2)。 2.当固定某个参变量(常为压力)f=4一Φ,四相平衡共存, 最大自由度fmax3。 2
2 !" #$%&'()*+,-./01(2345678978:!78 :";?&@(23A5BCDE;FGHIF!"#$%&'! ()*+,-#$%./0 !"%& 5 5 3 2 F max = - = = = - F + f c f c &'1#2(34#! ()*+,-.5 #2 F 1 2 3 4 5 *+, 4 3 2 1 0 6789 ":, ; :

恒压条件下三元体系状态图 恒压条件下的三元状态图是一个三维空间图 相区几何形态 立体 曲面 曲线 点 自由度 f=3 f=2 f=1 f=0 共存相 单相 双相 三相 四相点 三元体系任何状态图都不是完全的, 而是等温、等压、等组成图. 3
3 ?@ABC1;DEFGHIJ;KLMG #NOPQF R6 ST SU V *+, -./WWWWW-.XWWWWW-.YWWWWW-.Z &'# =# <# ;# "#V ;D67[PEFG\]H^_1! `Habca@cadeGff !"#$%&'()*+
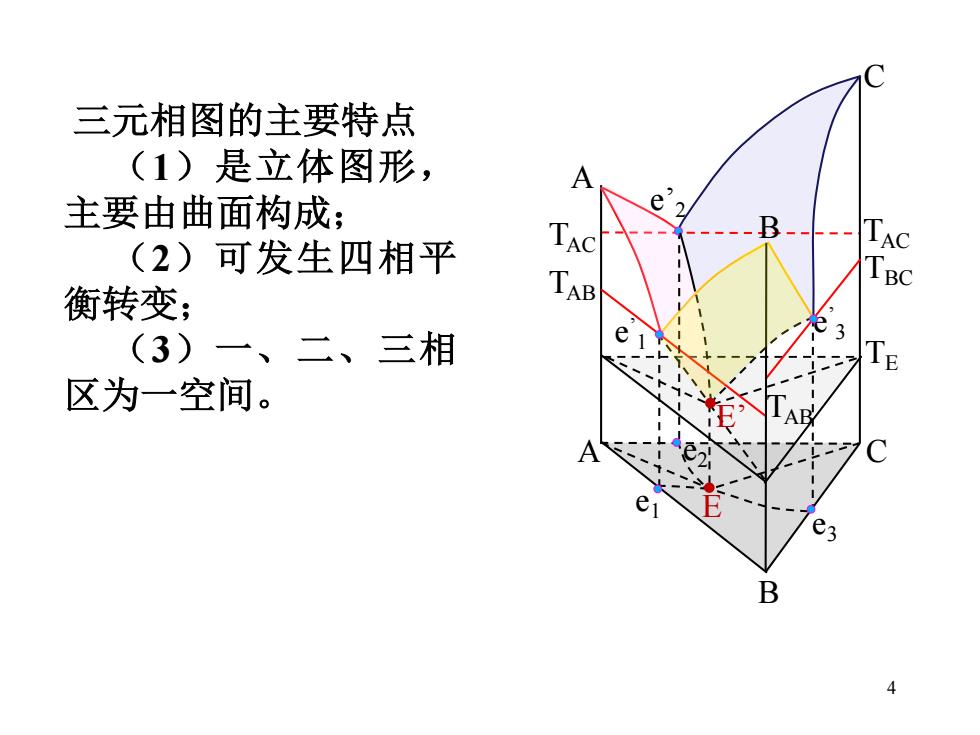
三元相图的主要特点 (1)是立体图形, 主要由曲面构成; (2)可发生四相平 TAC 衡转变; TAB (3) 一、二、三相 区为一空间。 2 B 4
4 三元相图的主要特点 (1)是立体图形, 主要由曲面构成; (2)可发生四相平 衡转变; (3)一 、二、三相 区为一空间。 A C B A C B e3 e1 e’ 3 e’2 e2 E TAC TAB TAC TAB TBC E’ e’ 1 TE

要点: 1.浓度三角形的规则; 2.重心、交叉、共轭位置的判定及关系式; 3.三元相图第一结晶区,第二结晶区,固相面、液 相面的立体构型等 4、投影图和等温截面图 5、冷却析晶过程及书写 6、罗策布规则、切线规则等及生成物类型的判定等 7、复杂三元相图的析晶过程 5
5 !"# $%&'()*+,-./ 0%&1234536789,:;?/ @% )ABCDEFGHIDJFGHIKBL3M BL,NOPQR S3TUCVRWXLC Y3Z[\G]^<_` a3bcd-.3ef-.R<ghijQ,:;R k3lm)ABC,\G]^
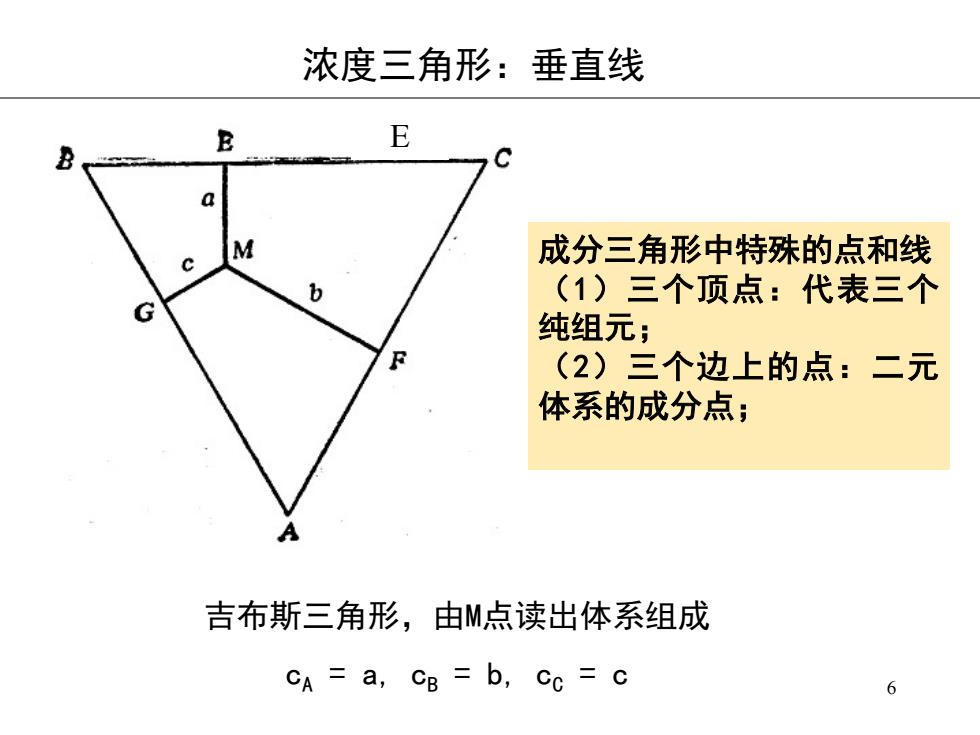
浓度三角形:垂直线 E E B Q M 成分三角形中特殊的点和线 b (1)三个顶点:代表三个 G 纯组元; F (2)三个边上的点:二元 体系的成分点; 吉布斯三角形,由M点读出体系组成 CA=a,CB=b,Cc=c 6
6 '()*+#nof ghi;jQ!+kVlm67de n& .WopWn' .WqpWn( .Wn E er;jQstu1VvU wYx;JyVz{|;J }dD~ wXx;JÄ1VzÅD 671erV~
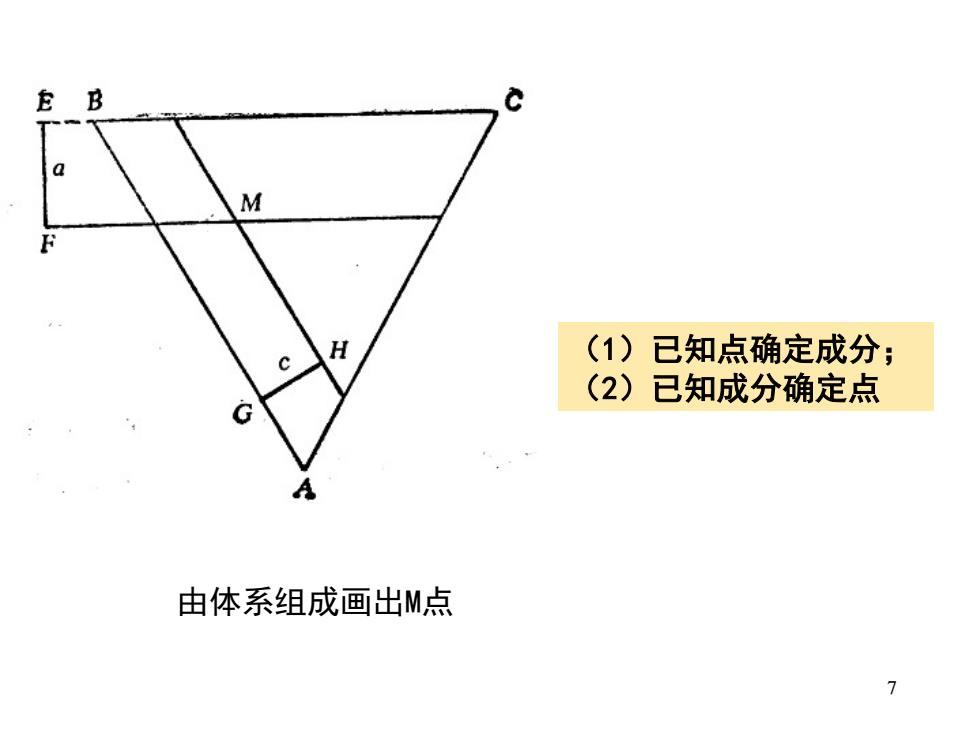
E B a M H c (1)已知点确定成分; (2)已知成分确定点 G 由体系组成画出M点 7
7 +67deÇmkV wYxÉÑVÖÜer~ wXxÉÑerÖÜV
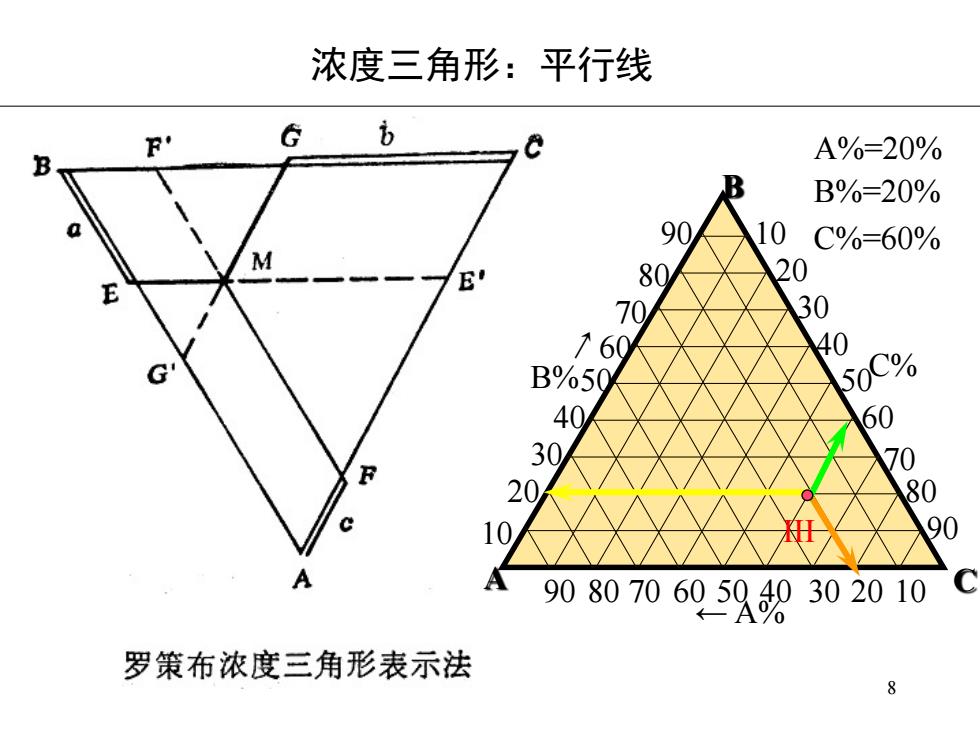
浓度三角形:平行线 R. G A%=20% B B B%=20% 10 C%=60% 0 20 E 0 30 60 40 G B 50C% 40 60 7 80 10 0 90807060598302010 罗策布浓度三角形表示法 8
8 '()*+#pqf A B 90 80 70 60 50 40 30 20 10 C 10 20 30 40 50 60 70 80 90 10 20 30 40 50 60 70 80 90 ← A% B% ↗ C% III A%=20% B%=20% C%=60%
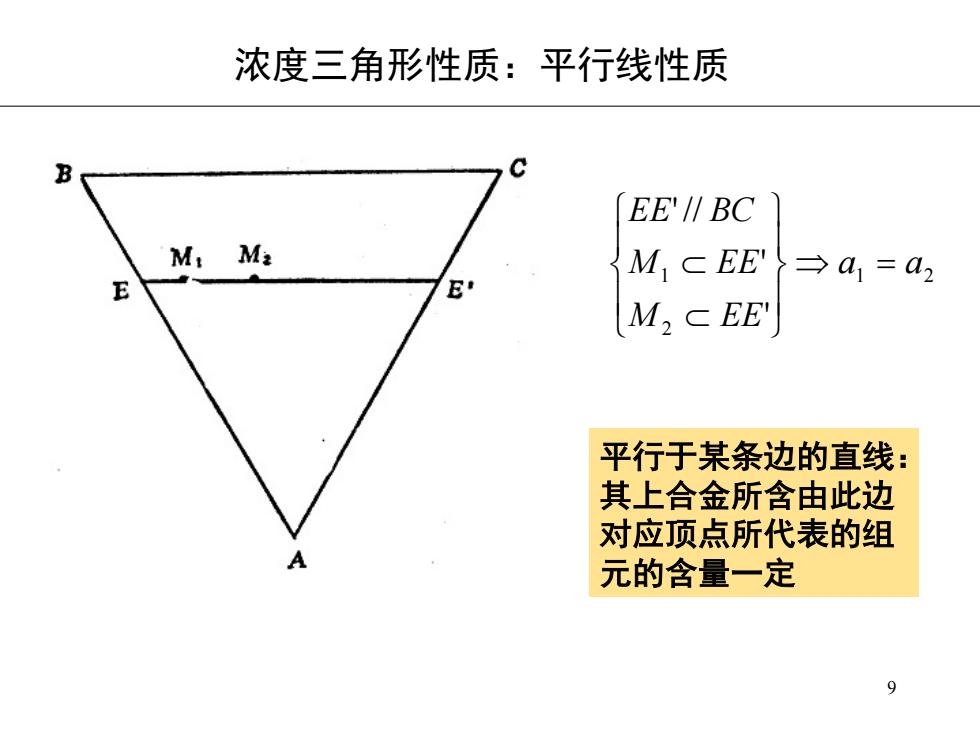
浓度三角形性质:平行线性质 B EEI∥BC M:Ma MCEE →a1=a2 E E M,CEE 平行于某条边的直线: 其上合金所含由此边 对应顶点所代表的组 元的含量一定 9
9 '()*+rs#pqfrs 1 2 2 1 ' ' '// a a M EE M EE EE BC Þ = ï þ ï ý ü ï î ï í ì Ì Ì $áàâA1äUz ãÄåçéè+ê ëíyVé{|1d D1èìIÜ
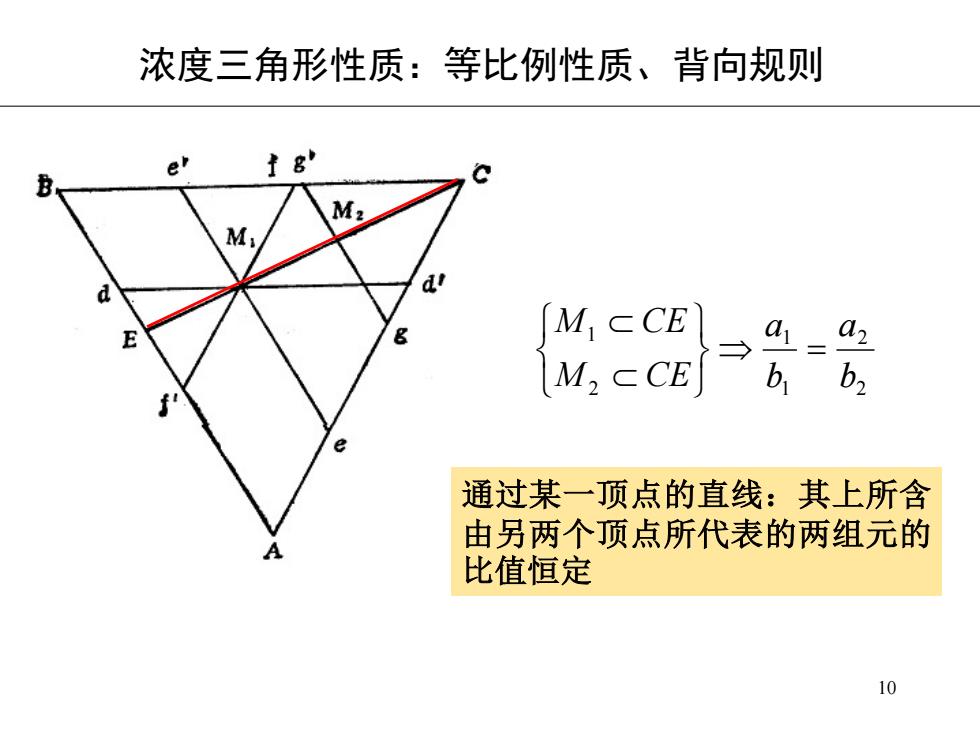
浓度三角形性质:等比例性质、背向规则 er f&' B M2 M, d d E MCCE 1= a2 M,CCE b2 e 通过某一顶点的直线:其上所含 由另两个顶点所代表的两组元的 比值恒定 10
10 '()*+rs#Rturs3vw-. 2 2 1 1 2 1 b a b a M CE M CE Þ = þ ý ü î í ì Ì Ì 通过某一顶点的直线:其上所含 由另两个顶点所代表的两组元的 比值恒定