
7.6.3扩散动力学范围 特点:VR>VD 7.6.3.1扩散控制的平板模式接触反应 AB 设经dt通过AB层单位截面的A摩尔数为dm B 由Fick第一定律得 dim=D.(dC) dc x dx dt dx Cx-Co0 设反应产物AB密度为p,分子量为M→dm= pdx M 再假设A在产物层中浓度呈线性分布: (-G d dx DCM → →X2 2DCM t=Kt dt pX Q 抛物线方程 K= 2DCoM
7.6.3 扩散动力学范围 特点:V R >> V D 7.6.3.1 扩散控制的平板模式接触反应 AB A B 设经dt通过AB层单位截面的 A摩尔数为dm 由Fick 第 一定律得 d C D dm ( )| x dx C =C 0 由Fick第 定律得 x dx D dt .( )| 设反应产物AB密度为 ,分子量为 M dx dm C A=C 0 0 设反应产物AB密度为 ,分子量为 M M dm x C ( )| = 0 x dx d C 再假设 A在产物层中浓度呈线性分布: dx x t Kt ρ 2DC M x 2 0 ρx DC M dt dx 0 ρ _ 抛物线方程 dt ρx 2DC M ρ K 0
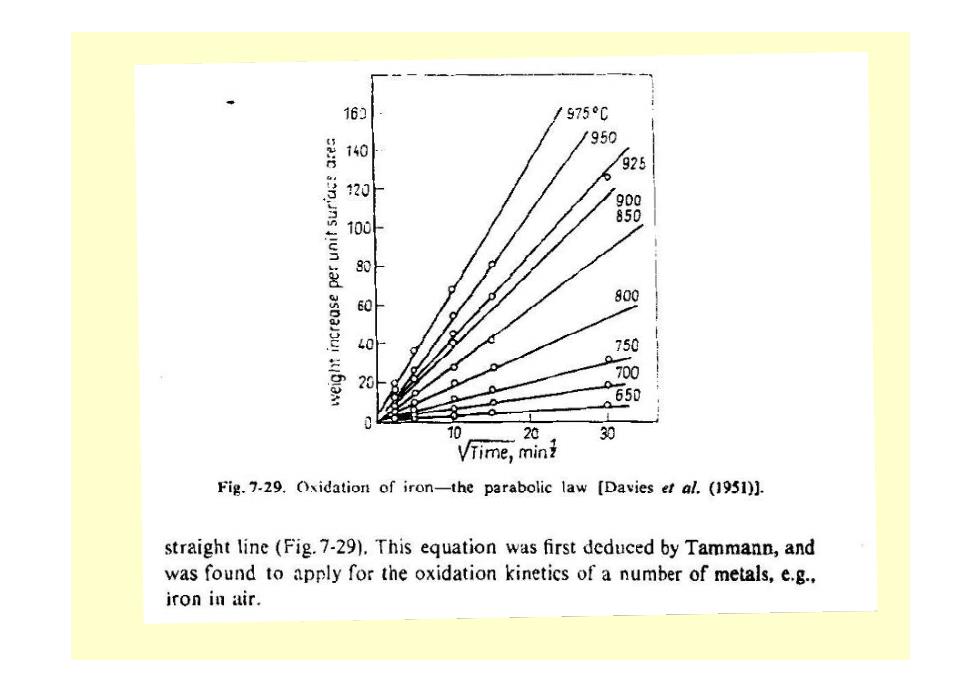
163 975℃ /950 925 sai snns jiun jad aspaour6aM 120 88 100 80 800 40 750 700 a650 20 30 VTime,min Fig.7-29.Oxidation of iron-the parabolic law [Davies et al.(1951)]. straight line (Fig.7-29).This equation was first deduced by Tammann,and was found to apply for the oxidation kinetics of a number of metals,e.g. iron in air
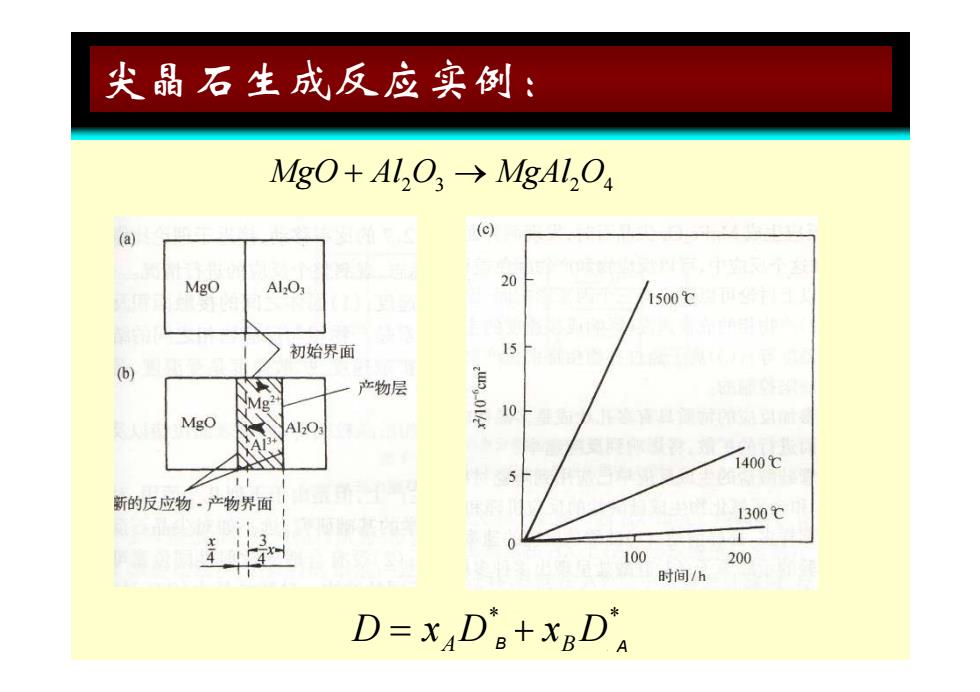
尖晶石生成反应实例: MgO+Al,O3→MgAl,O4 (a) (c) MgO Al2O 20 1500℃ 初始界面 (b) 产物层 10 MgO A120 1400 新的反应物·产物界面 1300℃ X I 100 200 时间/h D=xDe+xgD
尖晶石生成反应实例: MgO Al O M 23 24 g g 23 24 gAl O * * A A B D B D x D B x A

7.6.3.2粉末反应 扩散动力学范围 特点VR>VD 单晶固-固反应只是用于理论研究,便于初始和 边界条件的简化和确定,易于了解反应的基本 机理和反应影响因素(结构和取向),而实际 中的样品都是固体粉末。假设A颗粒于B基体中。 粉末反应的前期,符合 (平板模型)的抛物线 增长定律,但反应的中、 后期,与抛物线增长定 律有较大的偏差,且偏 差随反应生成物层厚度 的增加而增大
7.6.3.2 粉末反应 单晶固-固反应只是用于理论研究,便于初始和 扩散动力学范围 特点:VR >> VD 单晶固 固反应只是用于理论研究,便于初始和 边界条件的简化和确定,易于了解反应的基本 机理和反应影响因素(结构和取向) 而实际 机理和反应影响因素(结构和取向),而实际 中的样品都是固体粉末。假设A颗粒于B基体中。 粉末反应的前期,符合 (平板模型 的抛物线 ) 增长定律,但反应的中、 后期,与抛物线增长定 律有较大的偏差,且偏 差随反应 成物层厚度 生 的增加而增大
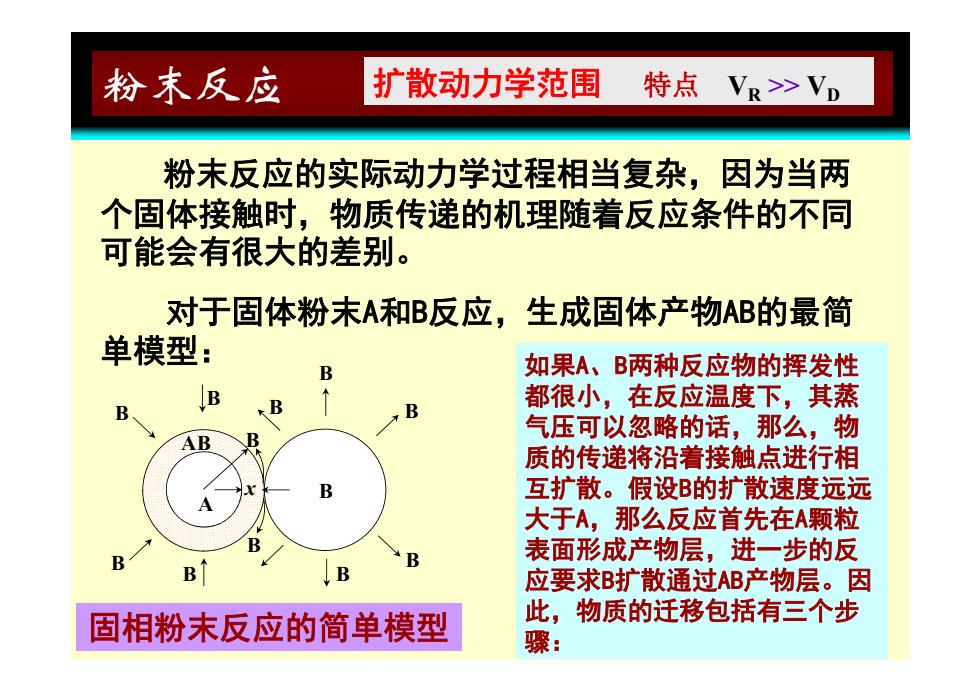
粉末反应 扩散动力学范围 特点VR>VD 粉末反应的实际动力学过程相当复杂,因为当两 个固体接触时,物质传递的机理随着反应条件的不同 可能会有很大的差别。 对于固体粉末A和B反应,生成固体产物AB的最简 单模型: B 如果A、B两种反应物的挥发性 B B 都很小,在反应温度下,其蒸 B 气压可以忽略的话,那么,物 AB 质的传递将沿着接触点进行相 互扩散。假设B的扩散速度远远 大于A,那么反应首先在A颗粒 B 表面形成产物层,进一步的反 B B 应要求B扩散通过AB产物层。因 固相粉末反应的简单模型 此,物质的迁移包括有三个步 骤:
粉末反应 扩散动力学范围 特点:VR >> VD 粉末反应的实际动力学过程相当复杂,因为当两 个固体接触时,物质传递的机理随着反应条件的不同 可能会有很大的差别。 对于固体粉末A和B反应,生成固体产物AB的最简 单模型: 如果A、B两种反应物的挥发性 都很小,在反应温度下,其蒸 气压可以忽略的话 那么 物 B B B B B 气压可以忽略的话,那么,物 质的传递将沿着接触点进行相 B 互扩散。假设B的扩散速度远远 A AB B x 大于A,那么反应首先在A颗粒 表面形成产物层,进一步的反 B 应要求B扩散通过AB产物层 因 B A B B B 应要求B扩散通过AB产物层。因 此,物质的迁移包括有三个步 骤: B 固相粉末反应的简单模型

粉末反应 ()物质B通过接触点以表面扩散的途径布满另一反应物 A的表面,或者B以蒸发的方式通过气相传递到A的表 面进行反应。 (2)在A表面形成一层致密的产物层AB,进一步的反应 通过B扩散穿过产物层AB发生。 (3)在A-AB界面上进行反应。 通常第一步是能够很快完成的,而 B 对于大多数固相反应而言,第二步往 B 往是最慢的。 AB B 注:如果形成的产物层是疏松的,或者 一旦形成就很快地从A表面脱离,那么B B 可以很快地到达A-AB界面,则在A-AB界 面上的化学反应速率将决定整个固相反应 B 的速率。(即前述。K。情形) B
粉末反应 ( )1 物质B通过接触点以表面扩散的途径布满另 通过接触点以表面扩散的途径布满另 反应物 一 A的表面,或者B以蒸发的方式通过气相传递到A的表 面进行反应。 (2) 在A表面形成一层致密的产物层AB,进一步的反应 通过B扩散穿过产物层AB发生。 (3) 在A-AB界面上进行反应。 通常第一步是能够很快完成的 而 B B B B B B 通常第 步是能够很快完成的,而 对于大多数固相反应而言,第二步往 往是最慢的。 B A AB B x 注:如果形成的产物层是疏松的,或者 一旦形成就很快地从A表面脱离,那么B 可以很快地到达A-AB界面,则在A-AB界 B B B B B , 面上的化学反应速率将决定整个固相反应 的速率。(即前述 VR << VD 情形)

粉末反应是非均相固相反应系统 反应基本条件:反应物间的机械接触,即在界面上进行反应 与接触面积F有关。 转化率(G):参与反应的反应物,在反应过程中被反应了的 体积分数(或质量分数)。 (①)设反应物颗粒呈球状,半径R,(A颗粒分散于B基体中) 则时间t后,颗粒外层有x厚度已被反应 G=R,-B,今R,-x=R(I-G R,3 Ro 则当前述反应控制时,固相反应动力学一 般方程为: G=KF1-G)° F:反应面积 d
粉末反应是非均相固相反应系统 反应基本条件:反应物间的机械接触,即在界面上进行反应 与接触面积F有关。 转化率(G): 参与反应的反应物,在反应过程中被反应了的 体积分数(或质量分数)。 (1) 设反应物颗粒呈 设反应物颗粒呈球状,半径R0 (A颗粒分散于B基体中) 则时间t 后,颗粒外层有x厚度已被反应 x 3 1 3 R -(R -x) R x 3 3 0 0 0 0 0 (1 G) R R (R x) G= R x R - R0 则当前述反应控制时,固相反应动力学一 般方程为: n =KF(1-G) dt dG F: 反应面积

A)粉末反应的杨德尔(Jander)模型 Jander模型把粉体颗粒视为规则的球形,设初 始半径为r,t时的产物层厚度为x。 6aw 4 4 r=%-'=r-r-x] 令转化率: f月 y x=r[1-(1-] 对比: R-x=R,1-G)3
A)粉末反应的杨德尔( Jander )模型 Jander 模型把粉体颗粒视为规则的球形,设初 始半径为 r ,t 时的产物层厚度为 x。 4 4 x 3 0 3 V r 4 3 ' () 3 V rx 4 3 3 r x 0 ' [ ( )] 3 VV V r rx r 令转化率: 3 3 3 3 ( ) 1 1 V r rx x y 3 0 y Vr r 1/3 x r y 1 1 31 0 0 对比: R x R (1-G)

粉末反应的Jander(杨德尔)模型 由于杨德尔模型的基本思路与平板 模型相同(即反应物B在产物层中 的浓度呈线性变化),因此,这里 的x与抛物线增长定律中的x相一 致。故有 x2 =2kt →(1-3-)=21r2x=1-1-] 实验证明,杨德尔模型适用于BaCO3、CaCO3 等碳酸盐与SiO2、Ti02、Mo03等氧化物的反应, 尤其是反应的初期。 2DCoM k= p
粉末反应的Jander(杨德尔)模型 由于杨德尔模型的基本思路与平板 x 模型相同(即反应物B在产物层中 的浓度呈线性变化),因此,这里 r 的 x 与抛物线增长定律中的 x 相一 致。故有 r 1/3 xr y 1 1 3 2 2 2 x k 2 t 1 1 y kt r 2 / 实验证明,杨德尔模型适用于BaCO3、CaCO3 等碳酸盐与SiO2、TiO2、MoO3等氧化物的反应 等氧化物的反应, 尤其是反应的初期

Jander equation BaCO3+SiO2>BaSiO3 CO2 0.03 Linear relationship is visible 890 0.02 870 0.01 00-0-0 840° 00 09 080。 000 000 r2[1-(1-Xa)32=2kt 0 020 4060 80100120 Time (min)
Jander equation BaCO + SiO BaSiO + CO 32 3 2 Linear relationship is visible 1 ~ 2 2 3 [1 (1 ) ] 2 B r X kt 10