
实验1-1氢原子光谱与里德伯常数的测定 光谱线系与原子结构之间存在内在的联系,光谱分析是研究原子结构的重要方法。 氢原子结构最为简单,它发出的光谱有明显的规律,很早就被人们所注意。100余年来, 人们对氢原子光谱结构的研究,不论是在实验方而还是在理论方面都取得了丰预成果 1885年瑞士物理学家巴耳未通过总结前人对氢原子光谱的测量结果发现了氢原子光谱 的规律,提出了著名的巴耳末公式。氢原子光谱规律的发现为玻尔理论的建立提供了坚 实的基础。1913年玻尔通过引入量子化条件,提出了用来解释氧原子光谱的玻尔模型。 这是原子物理学上的重大突破。1922年玻尔被授予诺贝尔物理学奖,以表彰他在研究原 子结构,特别是研究从原子发出的辐射方面所做的贡献。但玻尔理论并不能解释所观测 到的原子光谱的各种特征,而且对 于氢原子光诺的进一步解释也遇到了闲难,如巴耳未系 中最强线为何由两条谱线组成。玻尔理论遇到的困难促进了原子物理学和量子力学的发 展。20世纪初建立起来的量子力学圆满地解释了氢原子光谱线的分裂(电子不仅具有轨 道角动量,而且具有自旋角动量,二者相互作用的结果使光谱线分裂)以及其他复杂原子 光谱。1932年尤里(H.C.Urey)对重氨线系进行摄谱分析,发现了的同位素 通过巴耳末公式求得的里德伯常数是物理学中少数几个精确的常数之 ,已成为检 验原子理论可靠性的标准和测量其他基本物理常数的依据。因此,氢原子光谱的研究在 原子物理学和量子力学发展中起着重要作用。 【实验目的】 (1)测量可见光区氢原子光谱的波长,分析巴耳末系光谱线的规律性。 (2)测定氢原子的里德伯常数,了解近代物理学中的相关物理常数。 (3)掌握光光谱仪的分光原理和使用方法 (4)学习测量物质发射光谱的实验方法与技术。 【预习要求】 (1)氢原子有哪五个相互独立的光谱线系?各满足什么规律?哪个线系位于可见 -2-
౽ સ⧐౼Ⴑ౼ ድڅંԖ≠̷╜ϺఆᏒ وٴ䅞㏬㈨̻࣌ၽ㐀Ჱ䬡ႅౕڲ⮱ౕ㖁㈨ಎوٴ䅞ܳᲽ᭜ⵁ⾣࣌ၽ㐀Ჱ⮱䛺㺮∂ ⅏࣌ၽ㐀ᲱᰭͧキࢂಎႰܧࣾ⮱وٴ䅞ᰶᬻ᭫⮱㻱ᒸಎᒵᬖᅞ㷘ϧЙ∕ᘼಔಓಓ҆ᎡᲒಎ ϧЙᄦ⅏࣌ၽوٴ䅞㐀Ჱ⮱ⵁ⾣ಎ̺䃧᭜ౕ侹䲏䔅᭜ౕ⤳䃧䲏䘪ःᓄγ͝ⶂ ಔಛಛಘᎡ⦋ธ➖⤳႓უጡ㕠᱘䕇䓴ᕨ㐀ݺϧᄦ⅏࣌ၽوٴ䅞⮱≸䛼㐀ࣾ⣝γ⅏࣌ၽوٴ䅞 ⮱㻱ᒸಎܧγ㦄ऺ⮱ጡ㕠᱘ڙᐼ⅏࣌ၽوٴ䅞㻱ᒸ⮱ࣾ⣝ͧ⣨ᅁ⤳䃧⮱ᐧ⿸ӈγಇ ⮱ധಔಝಔಖᎡ⣨ᅁ䕇䓴ᑂڒ䛼ၽࡃУಎܧγ⩕Გ㼐䛷⅏࣌ၽوٴ䅞⮱⣨ᅁಸಎ 䔆᭜࣌ၽ➖⤳႓̷⮱䛺๔⾮ⵡಔಝಕಕᎡ⣨ᅁ㷘ᢵε䄧䉊ᅁ➖⤳႓ಎВ㶕ᒝЃౕⵁ⾣࣌ ၽ㐀Ჱಎ➦ݘ᭜ⵁ⾣ϻ࣌ၽܧࣾ⮱䒽ᄱ䲏և⮱䉎⡛ѳ⣨ᅁ⤳䃧Ꭳ̺㘪㼐䛷㻯≸ ݝ⮱࣌ၽوٴ䅞⮱ऱ➦ᒮಎ㔹́ᄦλ⅏࣌ၽوٴ䅞⮱䔈̭ₒ㼐䛷Ό䕴ݝγఝ䯫ಎຯጡ㕠᱘㈨ ͚ᰭᑧ㏬ͧ҂⩞͑䅞㏬㏱⣨ᅁ⤳䃧䕴ݝ⮱ఝ䯫Ӱ䔈γ࣌ၽ➖⤳႓হ䛼ၽ߈႓⮱ࣾ ᆂಕಓ̓㏗݊ᐧ⿸䊤Გ⮱䛼ၽ߈႓ళ␎ౝ㼐䛷γ⅏࣌ၽوٴ䅞㏬⮱ܳ㷯ಉ⩢ၽ̺ϲڤᰶ䒕 䖀㻿ߕ䛼ಎ㔹́ڤᰶ㜗㻿ߕ䛼ಎι㔲Ⱕο҉⩕⮱㐀Ҭوٴ䅞㏬ܳ㷯ಊВڣࣷЃฺᱯ࣌ၽ وٴ䅞ಔಝಖಕᎡᅑ䛹ಉਭਧਫ਼ಊᄦ䛺⅏䊃ᰩ㏬㈨䔈㵹ᥱ䅞ܳᲽಎࣾ⣝γ⅏⮱हѺ㉍ ⅅ䕇䓴ጡ㕠᱘ڙᐼⅯᓄ⮱䛹ᓤќ፥᭜➖⤳႓͚ᄾ܍⮱͗፥̭ಎጟͧᷭ 侹࣌ၽ⤳䃧ज䲍ᕔ⮱ᴴ۳হ≸䛼ڣЃധ᱙➖⤳፥⮱ӊᢛₑಎ⅏࣌ၽوٴ䅞⮱ⵁ⾣ౕ ࣌ၽ➖⤳႓হ䛼ၽ߈႓ࣾᆂ͚䊤Ɑ䛺㺮҉⩕ 侹Ⱋ⮱ ಉಔಊ≸䛼ज㻮ࡧوٴ⅏࣌ၽوٴ䅞⮱∏䪬ಎܳᲽጡ㕠᱘㈨وٴ䅞㏬⮱㻱ᒸᕔ ಉಕಊ≸Ⴧ⅏࣌ၽ⮱䛹ᓤќ፥ಎγ㼐䓾А➖⤳႓͚⮱Ⱕڠ⤳➖፥ ಉಖಊᢹᤎوٴᴲوٴ䅞З⮱ܳ࣌وٴ⤳হҬ⩕∂ ಉಗಊ႓≸䛼➖䉕ࣾᄱوٴ䅞⮱侹∂̻ឭᱜ 䶱㺮Ⅿ ಉಔಊ⅏࣌ၽᰶਗρ͗Ⱕο⠙⿸⮱وٴ䅞㏬㈨ಥ ऱ␎䋠ϭ͵㻱ᒸಥ ਗ͗㏬㈨Ѻλज㻮

光学测量技术实验第1章 光区 2)氢原子的巴耳末系谱线有何特点?如何分开各谱线 (3)如何利用氢原子光谱线计算相应的里德伯常数 (4)光彻分光的原理是什么?如何测量光栅光谱? 【实验原理】 氢原子光谱(hydrogen spectral series)可由氢气放电管发光的光谱中获得,也可由某 些星体发光的光谱中获得。人们最早对氢原子光谱的测量是在可见光区,1885年瑞士物 理学家巴耳末对已观察到的14条氢原子光谱线进行了研究,发现它们的波长入具有一定 的规律,并经验性地将可见光区的氢原子光谱线的波长归纳为下列关系: n=3.4.5. (1-1-1) 式中,B=364.56nm。式(1-1-1)一般称为巴耳末公式(Balmer formula),相应的这些谱线 称为巴耳末线系。 了更清楚地表明谱线的分布规律,1889年瑞典物理学家里德伯.R.Rydberg)把 式(1-1-1)改写为: n=3.4.5.(1-1-2) 式中,RH=4/B称为里德伯常数(Rydberg constant)。式(1-l-2)一般称为里德伯公式 (Rydberg formula) 在这些从实验得到的经验公式基础上,丹麦物理学家玻尔就原子模型提出两条基本 假设:①一个原子系统内当电子在特定轨道上绕核做圆周运动时,不向外辐射能量,这些 轨道就是电子保持能量不变的定态轨道:②电子从一个定态轨道跃迁到另一个定态轨道 时,会发生电磁辐射,其颜率完全由这两个定态轨道间的能量差来决定。根据玻尔的假设 并考虑原子核的影响,氢原子的定态轨道能量E,为: 2xue E.-一(4Ea产h'n - 式中,为约化质量:为电子电荷:h为普朗克常数:。为真空介电常数:m为电子质量: M:为氢原子核的质量 根据玻尔的假设,光谱线对应于氢原子中的电子从一个能级跃迁到另一个能级释放 出的能量。巴耳末线系是氢原子从n>2的状态跃迁到终态为2的状态时发出的光谱线 系,根据玻尔氢原子理论公式可推导出巴耳末线系满足的规律为 2π2e‘m (1-1-3) 式中,c为光速。 将式(1-13)和式(1-1-2)比较,可得里德伯常数为: 3
౾ ಥࡧوٴ ಉಕಊ⅏࣌ၽ⮱ጡ㕠᱘㈨䅞㏬ᰶ҂➦◦ಥ ຯ҂ܳᐭऱ䅞㏬ಥ ಉಖಊຯ҂ݖ⩕⅏࣌ၽوٴ䅞㏬䃎ツⰥᏁ⮱䛹ᓤќ፥ಥ ಉಗಊوٴᴲܳوٴ⮱࣌⤳᭜ϭ͵ಥ ຯ҂≸䛼وٴᴲوٴ䅞ಥ ⤳࣌侹 ⅏࣌ၽوٴ䅞ಉ੍ਫ਼ਗ਼ੑਖ਼ਜ਼ੋਫ਼ਫ਼ಊज⩞⅏⅁ᩫ⩢ノوٴࣾ⮱وٴ䅞͚㣤ᓄಎΌज⩞ ψᭌҀوٴࣾ⮱وٴ䅞͚㣤ᓄϧЙᰭᬖᄦ⅏࣌ၽوٴ䅞⮱≸䛼᭜ౕज㻮ࡧوٴಎಔಛಛಘᎡ⦋ธ➖ ⤳႓უጡ㕠᱘ᄦጟ㻯ᄌݝ⮱ಔಗ⅏࣌ၽوٴ䅞㏬䔈㵹γⵁ⾣ಎࣾ⣝ႰЙ⮱∏䪬ຊ ڤჇ̭ᰶ ⮱㻱ᒸಎᎣ㏼侹ᕔౝᄳज㻮ࡧوٴ⮱⅏࣌ၽوٴ䅞㏬⮱∏䪬ᑿ㏠̸݄ͧڠ㈨ಞ ຊಉ ಕ ಕ ౷ಗಉಖಎಗಎಘಎૡ ಉಔႱಔႱಔಊ ᐼ͚ಎಡಖಙಗಘಙਖ਼ᐼಉಔႱಔႱಔಊ̭㝙⼝ͧጡ㕠᱘ڙᐼಉਦਫ਼ਗ਼ਫ਼ಊಎⰥᏁ⮱䔆ψ䅞㏬ ⼝ͧጡ㕠᱘㏬㈨ ͧγᰡ⌲ẇౝ㶕ᬻ䅞㏬⮱ܳጰ㻱ᒸಎಔಛಛಝᎡ⦋ڥ⤳➖႓უ䛹ᓤќಉਯਸਸ੍ਫ਼ੑಊិ ᐼಉಔႱಔႱಔಊᩦۆuಞ ಔ ຊ ಉಔ ಕ ౷ಗ ಕ ಉಗ ಔ ಗ ౷ ಔ ಕ ಉਣਭ ಔ ಕಕ ౷ ಔ ಕ ಉಖಎಗಎಘಎૡ ಉಔႱಔႱಕಊ ᐼ͚ಎਣਭ ಉಗಒ ⼝ͧ䛹ᓤќ፥ಉਸ੍ਫ਼ੑੋਗ਼ਖ਼ਖ਼ಊᐼಉಔႱಔႱಕಊ̭㝙⼝ͧ䛹ᓤќڙᐼ ಉਸ੍ਫ਼ੑਗ਼ਫ਼ಊ ౕ䔆ψϻ侹ᓄݝ⮱㏼侹ڙᐼധ̷ಎͦ叓➖⤳႓უ⣨ᅁᅞ࣌ၽಸܧ͑ധ᱙ մ䃫ಞ௳ ̭͗࣌ၽ㈨㐌ڲᒀ⩢ၽౕ➦Ⴧ䒕䖀̷㐂ᵥևళক䓽ߕᬣಎ̺ाใ䒽ᄱ㘪䛼ಎ䔆ψ 䒕䖀ᅞ᭜⩢ၽԊᠮ㘪䛼̺अ⮱Ⴧᔮ䒕䖀ಟ௴ ⩢ၽϻ̭͗Ⴧᔮ䒕䖀䋰䓮ݝओ̭͗Ⴧᔮ䒕䖀 ᬣಎчࣾⷮ⩢⩌䒽ᄱಎڣ䶾⢴Ⴙڕ⩞䔆͑͗Ⴧᔮ䒕䖀䬡⮱㘪䛼ጛᲒ۠Ⴧᵦᢛ⣨ᅁ⮱մ䃫 Ꭳ㔰㭾࣌ၽᵥ⮱ᒞ৺ಎ⅏࣌ၽ⮱Ⴧᔮ䒕䖀㘪䛼ਔ ͧಞ ਔ ಉ౷ ಕວಕ ਹಗ ಉಗວຄಓಊಕ ಕ ಕ ಉ ਝਭ ਝਭ ᐼ͚ಎ ͧ㏓ࡃ䉕䛼ಟਹͧ⩢ၽ⩢㢤ಟ ͧᮛ᱄يٴ፥ಟຄಓ ͧⱌ⾧ϸ⩢፥ಟ ͧ⩢ၽ䉕䛼ಟ ਝਭ ͧ⅏࣌ၽᵥ⮱䉕䛼 ᵦᢛ⣨ᅁ⮱մ䃫ಎوٴ䅞㏬ᄦᏁλ⅏࣌ၽ͚⮱⩢ၽϻ̭͗㘪㏔䋰䓮ݝओ̭͗㘪㏔䛷ᩫ ܧ⮱㘪䛼ጡ㕠᱘㏬㈨᭜⅏࣌ၽϻಢಕ⮱⟣ᔮ䋰䓮ݝ㏵ᔮͧಕ⮱⟣ᔮᬣܧࣾ⮱وٴ䅞㏬ ㈨ಎᵦᢛ⣨ᅁ⅏࣌ၽ⤳䃧ڙᐼजᣕᄩܧጡ㕠᱘㏬㈨␎䋠⮱㻱ᒸͧಞ ಔ ຊ ಉ ಕວಕ ਹಗ ಉಗວຄಓಊಕ ਸ਼ಖ ಔ ਝਭ ಔ ಕಕ ౷ ಔ ಕ ಉಔႱಔႱಖಊ ᐼ͚ಎਸ਼ͧوٴ䕌 ᄳᐼಉಔႱಔႱಖಊহᐼಉಔႱಔႱಕಊ℁䒰ಎजᓄ䛹ᓤќ፥ͧಞ

物理实验教程—近代物理实险 0 2x2e‘m RH= (1-1-4) 4,h+2) 巴耳未开创了探索原子光谱线系规律性的研究,后来人们发现氢原子光谱在红外区 和紫外区也有很多条光谱线,构成很有规律的光谱线系。氢原子的各光谱线系分别以发 现者的名字来标记,其名称及表示公式分别为: 赖曼系(Lyman series))(紫外区) 是=R(信-) n=2.3,4. (1914年) 巴耳未系(Balmer series)(可见光区) 是-R(会-) =3,4,5, (1885年) 帕邢系(Paschen series)(近红外区) 是-R(你-) n=4,5,6, (1908年) 布喇开系(Brackett series)(红外区) 是-R(你-) n=5,6,7,. (1922年) 冯德系(Pfund series)(远红外区) 是=R(信-) n=6,7,8,. (1924年) 汉弗莱斯系(Humphreys srie)(远红外区)是=Rn(原一月) n=7,8,9, (1953年) 综合氢原子光谱谱系的理论公式,可用下面的普遍表达式来表示: =R(-) <n 对原子光谱的进一步研究发现,其他原子的光谱也具有氢原子光谱的这种特点。任 意原子A的里德伯常数可表示为: RA= 2xem (1-1-5) (4e)h'(1+ 由式(1-1-5)可知,随着原子核质量M的不同,原子的里德伯常数也不同。当M一 四时,有是=0,这时里德伯常数为 R。-2re (1-1-6) 由式(1-1-4),式(1-1-5)、式(1-1-6)可得R。与任意原子(如氢原子)的里德伯常数有下列 关系: R-Ra(1+元)-R(1+ (1-1-7) 4
౿ ਣਭ ಉ ಕວಕ ਹಗ ಉಗວຄಓಊಕ ਸ਼ಖ ಔ ਝਭ ಉಔႱಔႱಗಊ ጡ㕠᱘ᐭ݈γᣏ㉏࣌ၽوٴ䅞㏬㈨㻱ᒸᕔ⮱ⵁ⾣ಎऻᲒϧЙࣾ⣝⅏࣌ၽوٴ䅞ౕ㏏ใࡧ হ㉘ใࡧΌᰶᒵ็وٴ䅞㏬ಎᲱᒵᰶ㻱ᒸ⮱وٴ䅞㏬㈨⅏࣌ၽ⮱ऱوٴ䅞㏬㈨ܳݘВࣾ ⣝㔲⮱ऺႄᲒᴴ䃝ಎڣ口ऺࣷ㶕ڙᐼܳݘuಞ 䊃ᰩ㈨ಉਖ਼ਫ਼ಊಉ㉘ใࡧಊಔ ຊ ಉਣਭ ಔ ಔಕ ౷ ಔ ಕ ಡಕಎಖಎಗಎૡ ಉಔಝಔಗᎡಊ ጡ㕠᱘㈨ಉਦਫ਼ਫ਼ಊಉज㻮ࡧوٴಊ ಔ ຊ ಉਣਭ ಔ ಕಕ ౷ ಔ ಕ ಡಖಎಗಎಘಎૡ ಉಔಛಛಘᎡಊ ፂ䗏㈨ಉਵੋਖ਼ਫ਼ಊಉ䓾㏏ใࡧಊ ಔ ຊ ಉਣਭ ಔ ಖಕ ౷ ಔ ಕ ಡಗಎಘಎಙಎૡ ಉಔಝಓಛᎡಊ ጰᐭ㈨ಉਦਫ਼ੋਫ਼ಊಉ㏏ใࡧಊ ಔ ຊ ಉਣਭ ಔ ಗಕ ౷ ಔ ಕ ಡಘಎಙಎಚಎૡ ಉಔಝಕಕᎡಊ ۜᓤ㈨ಉਵਖ਼੍ਫ਼ಊಉ䔉㏏ใࡧಊ ಔ ຊ ಉਣਭ ಔ ಘಕ ౷ ಔ ಕ ಡಙಎಚಎಛಎૡ ಉಔಝಕಗᎡಊ ⅶᑄ㣞㈨ಉਭਜ਼ਫ਼ਫ਼ಊಉ䔉㏏ใࡧಊ ಔ ຊ ಉਣਭ ಔ ಙಕ ౷ ಔ ಕ ಡಚಎಛಎಝಎૡ ಉಔಝಘಖᎡಊ 㐩व⅏࣌ၽوٴ䅞䅞㈨⮱⤳䃧ڙᐼಎज⩕̸䲏⮱ᮛ䕺㶕䓫ᐼᲒ㶕ಞ ಔ ຊ ಉਣਭ ಔ ଂಕ ౷ ಔ ಕ ଂ ಠ ᄦ࣌ၽوٴ䅞⮱䔈̭ₒⵁ⾣ࣾ⣝ಎڣЃ࣌ၽ⮱وٴ䅞Όڤᰶ⅏࣌ၽوٴ䅞⮱䔆➦◦Ш ᘼ࣌ၽ ਥ ⮱䛹ᓤќ፥ज㶕ͧಞ ਣਥ ಉ ಕວಕ ਹಗ ಉಗວຄಓಊಕ ਸ਼ಖ ಔ ਝਥ ಉಔႱಔႱಘಊ ⩞ᐼಉಔႱಔႱಘಊजⴒಎ䮼Ɑ࣌ၽᵥ䉕䛼 ਝਥ⮱̺हಎ࣌ၽ⮱䛹ᓤќ፥Ό̺हᒀ ਝਥ ଲ ᬣಎᰶ ਝ ಡಓಎ䔆ᬣ䛹ᓤќ፥ͧಞ ਣ ಉ ಕວಕ ຄಗ ಉಗວຄಓಊಕ ਸ਼ಖ ಉಔႱಔႱಙಊ ⩞ᐼಉಔႱಔႱಗಊᐼಉಔႱಔႱಘಊᐼಉಔႱಔႱಙಊजᓄ ਣ ̻Шᘼ࣌ၽಉຯ⅏࣌ၽಊ⮱䛹ᓤќ፥ᰶ̸݄ ㈨ಞڠ ਣ ಉਣਥ ಔ ਝਥ ಉਣਭ ಔ ਝਭ ಉಔႱಔႱಚಊ
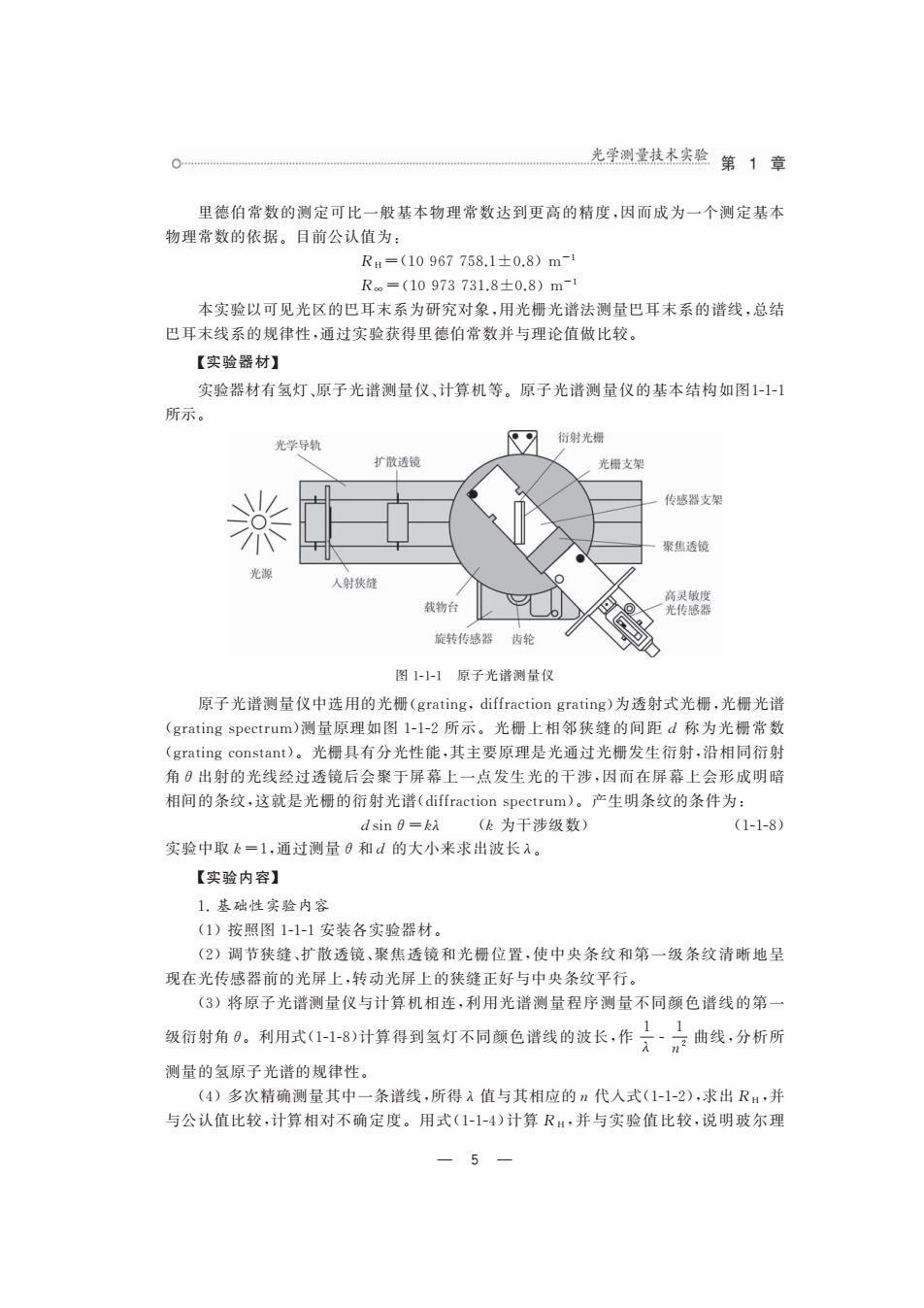
光学测量技术实验第1章 里德伯常数的测定可比一般基本物理常数达到更高的精度,因而成为一个测定基本 物理常数的依据。目前公认值 =(10967758.1±0.8)m R-(10973731.8±0.8m 本实验以可见光区的巴耳末系为研究对象,用光栅光谱法测量巴耳末系的谱线,总结 巴耳末线系的规律性,通过实验获得里德伯常数并与理论值做比较。 【实验器材】 实验器材有氢灯、原子光谱测量仪、计算机等。原子光谱测量仪的基本结构如图1-1-1 所示。 光学导 乙行射光标 光支架 传器支架 聚焦透链 射 载物台 免牧 图1-1原子光谱测量仪 原子光谱测量仪中选用的光摄(grating,.diffraction grating))为透射式光橱,光栅光 (grating spectrum)测量原理如图1-l-2所示。光栅上相邻狭缝的间距d称为光常贵 (grating constant》。光册具有分光性能,其主要原理是光通过光栅发生衍射,沿相同衍 角?出射的光线经过透镜后会聚于屏幕上一点发生光的干涉,因而在屏幕上会形成明暗 相间的条纹,这就是光栅的衍射光谱(d击iffraction spectrum)。产生明条纹的条件为: dsin0=k(k为干涉级数) (1-1-8) 实验中取k=1,通过测量0和d的大小来求出波长。 【实验内容】 1.基础性实验内容 (1)按照图1-1安装各实验器材。 (2)调节狭缝、扩散透镜、聚焦透镜和光橱位置,使中央条纹和第一级条纹清晰地呈 现在光传感器前的光屏上,转动光屏上的狭缝正好与中央条纹平行。 (3)将原子光谱测量仪与计算机相连,利用光谱测量程序测量不同颜色谱线的第 级衍射角。利用式(11-8)计算得到氢灯不同颜色谱线的被长,作·曲线,分析所 测量的氢原子光谱的规律性。 (4)多次精确测量中一条谱线,所得λ值与其相应的代入式(1-1-2),求出RH,并 与公认值比较,计算相对不确定度。用式(1-1-4)计算R,并与实验值比较,说明玻尔理 5
ಀ 䛹ᓤќ፥⮱≸Ⴧज℁̭㝙ധ᱙➖⤳፥䓫ݝᰡ倅⮱Ꮣಎ㔹̭ͧ͗≸Ⴧധ᱙ ➖⤳፥⮱ӊᢛⰛڙݺ䃑թͧಞ ਣਭ ಡಉಔಓಝಙಚಚಘಛಔಓಛಊಏಔ ਣ ಡಉಔಓಝಚಖಚಖಔಛಓಛಊಏಔ ᱙侹Вज㻮ࡧوٴ⮱ጡ㕠᱘㈨ͧⵁ⾣ᄦ䆎ಎ⩕وٴᴲوٴ䅞∂≸䛼ጡ㕠᱘㈨⮱䅞㏬ಎᕨ㐀 ጡ㕠᱘㏬㈨⮱㻱ᒸᕔಎ䕇䓴侹㣤ᓄ䛹ᓤќ፥Ꭳ̻⤳䃧թև℁䒰 侹கᱽ 侹கᱽᰶ⅏▜࣌ၽوٴ䅞≸䛼З䃎ツᱧぶ࣌ၽوٴ䅞≸䛼З⮱ധ᱙㐀ᲱຯఫಔႱಔႱಔ ఫಔႱಔႱಔ࣌ၽوٴ䅞≸䛼З ࣌ၽوٴ䅞≸䛼З͚䔶⩕⮱وٴᴲಉੑਫ਼ਖ਼ੑಎ੍ਫ਼ੋਗ਼ਖ਼ੑਫ਼ਖ਼ੑಊͧ䔼ᄱᐼوٴᴲಎوٴᴲوٴ䅞 ಉੑਫ਼ਖ਼ੑਜ਼ੋਫ਼ಊ≸䛼࣌⤳ຯఫಔႱಔႱಕوٴᴲ̷Ⱕ䗨⠚㑊⮱䬡䌊ਸ ⼝ͧوٴᴲ፥ ಉੑਫ਼ਖ਼ੑੋਗ਼ਖ਼ਖ਼ಊوٴᴲڤܳᰶوٴᕔ㘪ಎڣc㺮࣌⤳᭜وٴ䕇䓴وٴᴲࣾ⩌㵺ᄱಎ⇬Ⱕह㵺ᄱ 㻿ງܧᄱ⮱وٴ㏬㏼䓴䔼䪉ऻч㖇λᅼᎂ̷̭◦ࣾ⩌وٴ⊷⮱ಎ㔹ౕᅼᎂ̷чᒏᬻᯄ Ⱕ䬡⮱㏦ಎ䔆ᅞ᭜وٴᴲ⮱㵺ᄱوٴ䅞ಉ੍ਫ਼ੋਗ਼ਖ਼ਜ਼ੋਫ਼ಊϔ⩌ᬻ㏦⮱Уͧಞ ਸਖ਼ງಉੀຊ ಉੀ ͧ⊶㏔ಊ ಉಔႱಔႱಛಊ 侹͚ःੀಡಔಎ䕇䓴≸䛼ງহਸ ⮱๔ᄼᲒⅯܧ∏䪬ຊ 侹ڲღ ಔധᕔ侹ڲღ ಉಔಊᠶ⚔ఫಔႱಔႱಔႶ㷲ऱ侹கᱽ ಉಕಊ䄰㞯⠚㑊ព᪐䔼䪉㖇♓䔼䪉হوٴᴲѺ㒛ಎҬ͚๛㏦হす̭㏔㏦⌲ᮝౝॵ ⣝ౕوٴэᙌகݺ⮱وٴᅼ̷ಎ䒙وٴߕᅼ̷⮱⠚㑊ₐສ̻͚๛㏦Ꭰ㵹 ಉಖಊᄳ࣌ၽوٴ䅞≸䛼З̻䃎ツᱧⰥ䔋ಎݖ⩕وٴ䅞≸䛼⼸Ꮌ≸䛼̺ह䷉㞟䅞㏬⮱す̭ ㏔㵺ᄱ㻿ງݖ⩕ᐼಉಔႱಔႱಛಊ䃎ツᓄݝ⅏▜̺ह䷉㞟䅞㏬⮱∏䪬ಎ҉ ಔ ຊ႗ಔ ಕ ᰟ㏬ಎܳᲽ ≸䛼⮱⅏࣌ၽوٴ䅞⮱㻱ᒸᕔ ಉಗಊ็⁎≸䛼ڣ̭͚䅞㏬ಎᓄຊ թ̻ڣⰥᏁ⮱ АڒᐼಉಔႱಔႱಕಊಎⅯܧਣਭ ಎᎣ ̻ڙ䃑թ℁䒰ಎ䃎ツⰥᄦ̺ჇᏓ⩕ᐼಉಔႱಔႱಗಊ䃎ツ ਣਭ ಎᎣ̻侹թ℁䒰ಎ䄡ᬻ⣨ᅁ⤳
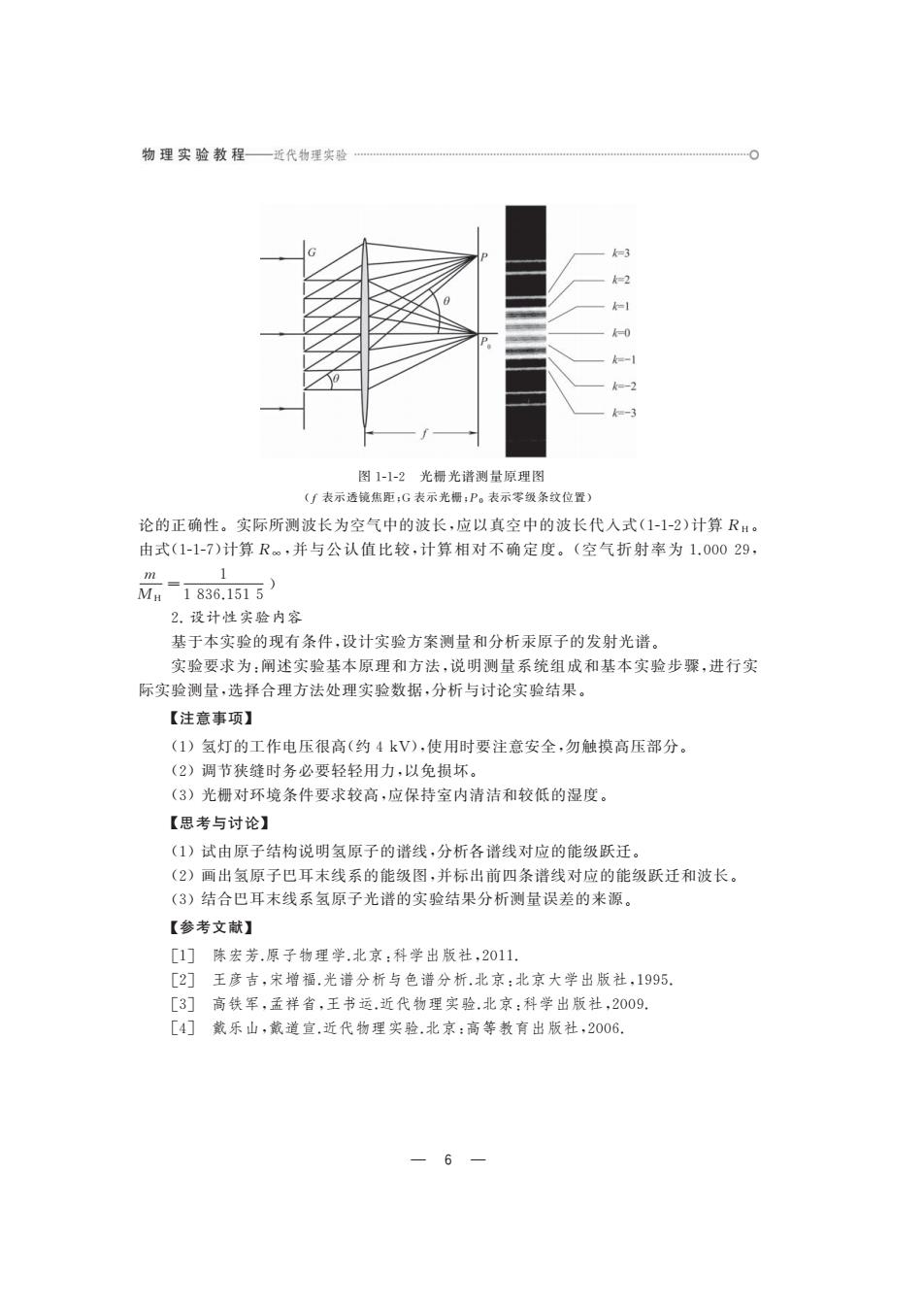
物理实验教程一近代物理实验. .0 图1-1-2光栅光谱测量原理图 (∫表示透镜焦距:G表示光栅,P。表示零级条纹位置) 论的正确性。实际所测波长为空气中的波长,应以真空中的波长代入式(1-1-2)计算RH。 由式(1-1-7)计算R。,并与公认值比较,计算相对不确定度。(空气折射率为1.00029, 1 M-1836.1515) 2.设计性实验内容 基于本实验的现有条件,设计实验方案测量和分析汞原子的发射光谱。 实验要求为:阐述实验基本原理和方法,说明测量系统组成和基本实验步骤,进行实 际实验测量,选择合理方法处理实验数据,分析与讨论实验结果。 【注意事项】 (1)氢灯的工作电压很高(约4kV),使用时要注意安全,勿触摸高压部分。 (2)调节狭缝时务必要轻轻用力,以免损坏。 (3)光栅对环境条件要求较高,应保持室内清洁和较低的湿度。 【思考与讨论】 (1)试由原子结构说明氢原子的谱线,分析各谱线对应的能级跃迁。 (2)画出氢原子巴耳末线系的能级图,并标出前四条谱线对应的能级跃迁和波长。 (3)结合巴耳末线系氢原子光谱的实验结果分析测量误差的来源。 【参考文献】 [1]陈宏芳.原子物理学.北京:科学出版社,2011. [2]王彦吉,宋增福.光谱分析与色谱分析北京:北京大学出版社,1995 [3]高铁军,孟祥省,王书运.近代物理实验.北京:科学出版社,2009. [4]戴乐山,戴道宣.近代物理实验.北京:高等教有出版社,2006
ಁ ఫಔႱಔႱಕوٴᴲوٴ䅞≸䛼࣌⤳ఫ ಉ 㶕䔼䪉♓䌊ಟਬ 㶕وٴᴲಟਠಓ 㶕䰣㏔㏦Ѻ㒛ಊ 䃧⮱ₐᕔ䭲≸∏䪬ͧ⾧⅁͚⮱∏䪬ಎᏁВⱌ⾧͚⮱∏䪬АڒᐼಉಔႱಔႱಕಊ䃎ツਣਭ ⩞ᐼಉಔႱಔႱಚಊ䃎ツਣ ಎᎣ̻ڙ䃑թ℁䒰ಎ䃎ツⰥᄦ̺ჇᏓಉ⾧⅁ៅᄱ⢴ͧಔಓಓಓಕಝಎ ਝਭ ಉ ಔ ಔಛಖಙ౹ಔಘಔಘಊ ಕ䃫䃎ᕔ侹ڲღ ധλ᱙侹⮱⣝ᰶУಎ䃫䃎侹ᵵ≸䛼হܳᲽ↋࣌ၽ⮱ࣾᄱوٴ䅞 侹㺮Ⅿͧಞ䬽䔝侹ധ᱙࣌⤳হ∂ಎ䄡ᬻ≸䛼㈨㐌㏱হധ᱙侹ₒ俑ಎ䔈㵹 䭲侹≸䛼ಎ䔶᠖व⤳∂ั⤳侹ᢛಎܳᲽ̻䃕䃧侹㐀 ∕ᘼθ䶦 ಉಔಊ⅏▜⮱ጒ҉⩢ࢸᒵ倅ಉ㏓ಗ਼ಊಎҬ⩕ᬣ㺮∕ᘼႶڕಎࠬ㼓ᦥ倅ࢸ䘕ܳ ಉಕಊ䄰㞯⠚㑊ᬣߎᓲ㺮䒨䒨⩕߈ಎВٺᢌ౼ ಉಖಊوٴᴲᄦ⣜ධУ㺮Ⅿ䒰倅ಎᏁԊᠮბڲ∮⌲হ䒰ѻ⮱⎬Ꮣ ᕊ㔰̻䃕䃧 ಉಔಊ䄂⩞࣌ၽ㐀Ჱ䄡ᬻ⅏࣌ၽ⮱䅞㏬ಎܳᲽऱ䅞㏬ᄦᏁ⮱㘪㏔䋰䓮 ಉಕಊ⩨ܧ⅏࣌ၽጡ㕠᱘㏬㈨⮱㘪㏔ఫಎᎣᴴݺܧఈ䅞㏬ᄦᏁ⮱㘪㏔䋰䓮হ∏䪬 ಉಖಊ㐀वጡ㕠᱘㏬㈨⅏࣌ၽوٴ䅞⮱侹㐀ܳᲽ≸䛼䄜ጛ⮱Გ⎽ ࣯㔰᪴⡛ ೂಔೄ 䭵Ⴜ㟠࣌ၽ➖⤳႓ࡄϙಞ႓ܧ❴ಎಕಓಔಔ ೂಕೄ ⢸ᒓशಎႸ⺼وٴ䅞ܳᲽ̻㞟䅞ܳᲽࡄϙಞࡄϙ๔႓ܧ❴ಎಔಝಝಘ ೂಖೄ 倅䧮ۈಎႌ⺒Ⱞಎ⢸Γ䓽䓾А➖⤳侹ࡄϙಞ႓ܧ❴ಎಕಓಓಝ ೂಗೄ ᝡͽᆞಎᝡ䖀ა䓾А➖⤳侹ࡄϙಞ倅ぶ᪆㗟ܧ❴ಎಕಓಓಙ