
实验3-3电子自旋共振 电子自旋共振(Electron Spin Resonance,ESR)是指电子自旋磁矩在磁场中因吸收电磁辐射而 发生的共振跃迁现象。这种共振跃迁只能发生在原子的固有磁矩不为零的顺磁物质中,因此被称为 电子顺破共振(electron paramagnetic resonance,EPR):因为分子和固体中的磁矩主要是电子自旋磁 矩的贡献,所以又被称为电子自旋共振。1924年美籍奥地利物理学家泡利(Wolfgang Erst Pauli) 首先提出了电子自旋的概念 1945年获得诺贝尔物理 奖。1944年前苏联的扎 Yevge Zavo1sky)首次观察到了电子顺磁共振现象。1954年开始电子自旋共振逐渐发展成为一项新的波谱 学技术,被用于科学研究和生产应用。 波谱学是研究电磁辐射与物质共振相互作用的规律,用以测定分子、原子和核的能级结构。电 子自旋共振也称电子质磁共振是磁共振波善学的一个分支,电子自旋共振研究的对象是具有不成对 电子的原子、分子或固体,例如自由基、三重态分子、过渡金属离子、稀土离子及固体中某些局部 品格缺陷等。 ESR技术可以检测浓度极低的不成对电子,精确地分析这些不成对电子所处的位置及 其能态等信息。因此,ESR技术是探素物质微观结构和运动状态的重要手段。 电子自旋共振技术在物理、化学、生物、医药等各个领域获得了广泛的应用。在物理学中,通 过ESR技术可鉴别出品格的位置和顺磁物质的对称性,获得原子的有效质量、核自旋、核磁矩和核 四极矩等信息。在化学分析和结构分析方面,通过ESR技术研究谱线的精细结构和朗德因子的不对 称性。 可鉴别出未知的过液金属 格的缺 判别同一离子的几种 在生物等 自旋标记技术可用ESR来探索生物体系的结构和生物反应的机制。为了探索更多的与物质结构有关 的,还经常在不同的温度、额率或微波功率等环境下进行ESR测量。在实际应用方面,ESR技术可 用来测量磁场强度、检测杂质和研究辐射损伤等。 与核磁共振相出,申子自旋共振在基本概今和基本原理上有很多相似之处,但在技术上更容易 实现,在射须波段和微波波段均可实现。因此,在本实验的具体内容中设计了2个系列实验项目 分别为实验33-1射缬电子自旋共振和实验332微波电子自旋共振。通过这两个实验项目,学 习电子自旋共振基本原理,系统地掌握射频法和微波法电子自旋共振的实验方法和实验技术。 【实验原理】 一.原子的自旋磁矩 原子中的电子在沿轨道运动的同时具有自旋,其自旋角动量为 Ps=√SS+dh (3-31) 式中S是电子自旋量子数,S=1/2。电子的自旋角动量P、与自旋磁矩μ、间的关系为 4=-82mP (3-3-2) Hs =gHaS(S+1) 式中m,为电子质量:”g= eh ,称为玻尔磁子:g为电子的朗德因子,具体表示为 2m。 g=1+W+)-(L+)+SS+) (3-3-3) 2.J(J+1)
实验 3-3 电子自旋共振 电子自旋共振(Electron Spin Resonance,ESR)是指电子自旋磁矩在磁场中因吸收电磁辐射而 发生的共振跃迁现象。这种共振跃迁只能发生在原子的固有磁矩不为零的顺磁物质中,因此被称为 电子顺磁共振(electron paramagnetic resonance,EPR);因为分子和固体中的磁矩主要是电子自旋磁 矩的贡献,所以又被称为电子自旋共振。1924 年美籍奥地利物理学家泡利(Wolfgang Ernst Pauli) 首先提出了电子自旋的概念,1945 年获得诺贝尔物理学奖。1944 年前苏联的扎沃伊斯基(Yevgeny Zavoisky)首次观察到了电子顺磁共振现象。1954 年开始电子自旋共振逐渐发展成为一项新的波谱 学技术,被用于科学研究和生产应用。 波谱学是研究电磁辐射与物质共振相互作用的规律,用以测定分子、原子和核的能级结构。电 子自旋共振也称电子顺磁共振是磁共振波谱学的一个分支,电子自旋共振研究的对象是具有不成对 电子的原子、分子或固体,例如自由基、三重态分子、过渡金属离子、稀土离子及固体中某些局部 晶格缺陷等。ESR 技术可以检测浓度极低的不成对电子,精确地分析这些不成对电子所处的位置及 其能态等信息。因此,ESR 技术是探索物质微观结构和运动状态的重要手段。 电子自旋共振技术在物理、化学、生物、医药等各个领域获得了广泛的应用。在物理学中,通 过 ESR 技术可鉴别出晶格的位置和顺磁物质的对称性,获得原子的有效质量、核自旋、核磁矩和核 四极矩等信息。在化学分析和结构分析方面,通过 ESR 技术研究谱线的精细结构和朗德因子的不对 称性,可鉴别出未知的过渡金属离子或晶格的缺陷,判别同一离子的几种价态。在生物学中,通过 自旋标记技术可用 ESR 来探索生物体系的结构和生物反应的机制。为了探索更多的与物质结构有关 的,还经常在不同的温度、频率或微波功率等环境下进行 ESR 测量。在实际应用方面,ESR 技术可 用来测量磁场强度、检测杂质和研究辐射损伤等。 与核磁共振相比,电子自旋共振在基本概念和基本原理上有很多相似之处,但在技术上更容易 实现,在射频波段和微波波段均可实现。因此,在本实验的具体内容中设计了 2 个系列实验项目, 分别为实验 3-3-1 射频电子自旋共振和实验 3-3-2 微波电子自旋共振。通过这两个实验项目,学 习电子自旋共振基本原理,系统地掌握射频法和微波法电子自旋共振的实验方法和实验技术。 【实验原理】 一.原子的自旋磁矩 原子中的电子在沿轨道运动的同时具有自旋,其自旋角动量为 pS = S(S +1) (3-3-1) 式中 S 是电子自旋量子数, S =1/ 2 。电子的自旋角动量 pS 与自旋磁矩 μS 间的关系为 ( ) 2 1 e S B e g m g S S = − = + μS S p (3-3-2) 式中 me 为电子质量; e B m e 2 = ,称为玻尔磁子;g 为电子的朗德因子,具体表示为 2 ( 1) ( 1) ( 1) ( 1) 1 + + − + + + = + J J J J L L S S g (3-3-3)

J和L为原子的总角动量量子数和轨道角动量量子数,J=L±S。对于单电子原子,原子的角动量 和磁矩由单个电子决定:对于多电子原子,原子的角动量和磁矩由价电子决定。含有单电子或未偶 电子的原子处于基态时,L0,L+SS12,此时原子的角动量和磁矩等价于单个电子的自旋角到 量和自旋磁矩 二。电子自旋共振 在唯象理论中,申子自你好像一个高速自转的“萨螺”,其磁矩在外加相定做场的作用下会发中 拉莫尔进动,这种 受到材料内部阻尼作用的 幅度会逐渐减 层后磁拓 亭留在外磁场 的方向上。如果在加外磁场的同时,在垂直于外场的方向加一个高顿电感场 当电场的频率 磁矩进动的频率一致的时候,电磁场能量将被强烈吸收,这就是共振现象。被吸收的能量为磁矩提 供克服阻尼的动力,使进动能够维持下去。从量子力学的观点看,共振是指在某一特定外磁场作用 下,电陵场与磁矩间相互作用而发生塞曼能级间的感应跃迁。 当存在外磁场时,电子的磁矩与外磁场B的相互作用能为 E=HsB,=B (3-3-4) 式中为磁矩在外磁场方向上的分量,即 He-82m Mh-gM.o (3-3-5) 式中M,=±行分裂的能级为 E,=84R (3-3-6 E,=-784,8 能级间的能量差为 △E=g4B, (3-3-7) 根据磁共振原理,如果在垂直于B。平面内施加一个角频率等于(频率为v)的交变磁场B1, 当满足条件 @h=h=△E=g4B (3-3-8) 时,电子就会吸收此交变磁场的能量,实现能级间的跃迁,这就是电子自旋共振现象。电子的旋磁 比为y= 2m8,则式(3-38)可以写为一个等效的式子 0=YB (3-3-9) 为了满足式(3-3-8)或式(3-3-9),实验中的交变磁场B1可以由射频线圈产生,也可以由微波 谐振腔产生,由此对应两种实验方法,即射频法电子自旋共振和微波法电子自旋共振。 三.朗德g因子 正如以上所描述的,g因子不仅反映了原子或者离子晶体中电子自旋一轨道相互作用的大小, 也反映了塞曼能级分裂的宽度,在本质上显示局部磁场的特征。 g因子的理论计算是一个复杂的问圈,实际上只能对某些比较简单的情况进行计算。在过渡族
J 和 L 为原子的总角动量量子数和轨道角动量量子数, J = L S 。对于单电子原子,原子的角动量 和磁矩由单个电子决定;对于多电子原子,原子的角动量和磁矩由价电子决定。含有单电子或未偶 电子的原子处于基态时,L=0,J=L+S=S=1/2,此时原子的角动量和磁矩等价于单个电子的自旋角动 量和自旋磁矩。 二.电子自旋共振 在唯象理论中,电子自旋好像一个高速自转的“陀螺”,其磁矩在外加恒定磁场的作用下会发生 拉莫尔进动,这种运动受到材料内部阻尼作用的影响,幅度会逐渐减小,最后磁矩将停留在外磁场 的方向上。如果在加外磁场的同时,在垂直于外磁场的方向加一个高频电磁场,当电磁场的频率与 磁矩进动的频率一致的时候,电磁场能量将被强烈吸收,这就是共振现象。被吸收的能量为磁矩提 供克服阻尼的动力,使进动能够维持下去。从量子力学的观点看,共振是指在某一特定外磁场作用 下,电磁场与磁矩间相互作用而发生塞曼能级间的感应跃迁。 当存在外磁场时,电子的磁矩与外磁场 B0 的相互作用能为 E B = = μS 0 B Sz 0 (3-3-4) 式中 Sz 为磁矩在外磁场方向上的分量,即 2 Sz z z B e e g M gM m = = (3-3-5) 式中 1 2 M z = 。分裂的能级为 0 0 1 2 1 2 a B b B E g B E g B = = − (3-3-6) 能级间的能量差为 = E g B B 0 (3-3-7) 根据磁共振原理,如果在垂直于 B0 平面内施加一个角频率等于 ω0(频率为 )的交变磁场 B1, 当满足条件 0 0 B = = = h E g B (3-3-8) 时,电子就会吸收此交变磁场的能量,实现能级间的跃迁,这就是电子自旋共振现象。电子的旋磁 比为 g m e e 2 = ,则式(3-3-8)可以写为一个等效的式子 0 0 = B (3-3-9) 为了满足式(3-3-8)或式(3-3-9),实验中的交变磁场 B1 可以由射频线圈产生,也可以由微波 谐振腔产生,由此对应两种实验方法,即射频法电子自旋共振和微波法电子自旋共振。 三.朗德 g 因子 正如以上所描述的,g 因子不仅反映了原子或者离子晶体中电子自旋—轨道相互作用的大小, 也反映了塞曼能级分裂的宽度,在本质上显示局部磁场的特征。 g 因子的理论计算是一个复杂的问题,实际上只能对某些比较简单的情况进行计算。在过渡族

或稀土金属品体中,由于原子排列的空间周期性,会产生一个周期性的带电粒子静电相互作用场(品 场)。晶场的作用倾向于“猝灭”轨道角动量,自旋一轨道耦合作用又倾向于再生轨道角动量,因此 8的数值反映了这两种相互作用竞争的结果。在晶体中,还存在电子自旋与核磁矩之间的作用,使 得g的数值在一个比较大的范围内变化,并使电子自旋共振波谱出现复杂的精细结构。晶体中8因 子不一定是各向同性的,只有对某些晶体类型,如立方体、四方体和八面体等g因子是各向同性的。 一般情况下g因子出现各向异性的特征,因而共振场的数值与外加磁场的方向相对于晶轴的取向有 关,这种情况下g因子的计算相当复杂,甚至不可能。因此g因子的数值往往是从实验上确定的 四.线宽和弛豫 选用的实验样品为密封于一段玻璃管中的有机自由基DPH(二苯基-苦基肼基),其分子式为 (C,H)2N-NCH,NO,),结构式如图331所示。在中间的N原子少一个共价键,有一个未配对的 自由电子,这个自由电子就是实验研究的对象。实验表明,自由基的g值(DPPH的公认g值为 2.0038 十分接近自由电子的g值(2.0023) 实际上样品是一个含有大量不成对的电子自旋所组成的系统,在 磁场中只分裂为二个塞曼能级。在热平衡时,分布于各塞曼能级上的 粒子数服从波耳兹曼分布,即低能级上的粒子数总比高能级的多 些,因此,即使粒子数因感应辐射由高能级跃迁到低能级的概率和因 感应吸收由低能级跃迁到高能级的 相等,但由于低能级的粒子数 比高能级的多,也是感应吸收占优势,从而为观测样品的磁共振吸收 图33-1DPPH的结构 信号提供可能性。随者高低能级上粒子数差的减小,以致趋于零,则观测不到共振现象,即所谓饱 和。但实际上共振现象仍可继续发生,这是弛豫过程在起作用,弛豫过程使整个系统有恢复到玻耳 兹曼分布的趋势,两种作用的综合效应,使自旋系统达到动态平衡,电子自旋共振现象就能维持下 电子自旋共振有两种弛豫过程:自旋一品格弛豫和自旋一自旋弛豫。电子自旋与品格交换能量, 使得处在高能级的粒子把一部分能量传给晶格,从而返回低能级,这种作用称为自旋一晶格驰豫, 由自旋一晶格弛豫时间T表征。自旋粒子相互之间交换能量,使它们的旋进相位趋于随机分布,这 种作用称自旋一自旋 由自旋一自旋弛像时间用工,表征。弛豫过程越快,谱线就越宽。通过测 量谱线半高宽4仙可估算自旋一自旋弛豫时间2,二者关系为 42 (3-3-10) T 本实验中分别用射频法和微波法实现电子自旋共振,两种方法中交变磁场B:的频率不同,因而 实验装置有很大差异。射频法电子自旋共振实验中交变磁场B1是由射频线圈产生的,频率较低,接 收信号的装置与核磁共振实验类似,采用射频线圈结合振荡电路:微波法电子自旋共振实验中交变 磁场是由微波提供的,频率更高,采微波系统提供交变磁场并接收电子自旋共振信号。 实验3-3-1射频电子自旋共振 【实验目的】 自旋共振信号的实验技术。 3.测定DPPH自由基的g因子、共振线宽和弛豫时间T
或稀土金属晶体中,由于原子排列的空间周期性,会产生一个周期性的带电粒子静电相互作用场(晶 场)。晶场的作用倾向于“猝灭”轨道角动量,自旋—轨道耦合作用又倾向于再生轨道角动量,因此 g 的数值反映了这两种相互作用竞争的结果。在晶体中,还存在电子自旋与核磁矩之间的作用,使 得 g 的数值在一个比较大的范围内变化,并使电子自旋共振波谱出现复杂的精细结构。晶体中 g 因 子不一定是各向同性的,只有对某些晶体类型,如立方体、四方体和八面体等 g 因子是各向同性的。 一般情况下 g 因子出现各向异性的特征,因而共振场的数值与外加磁场的方向相对于晶轴的取向有 关,这种情况下 g 因子的计算相当复杂,甚至不可能。因此 g 因子的数值往往是从实验上确定的。 四.线宽和弛豫 选用的实验样品为密封于一段玻璃管中的有机自由基 DPPH(二苯基-苦基肼基),其分子式为 6 5 2 6 2 2 3 (C H ) N- N C H (NO ) ,结构式如图 3-3-1 所示。在中间的 N 原子少一个共价键,有一个未配对的 自由电子,这个自由电子就是实验研究的对象。实验表明,自由基的 g 值(DPPH 的公认 g 值为 2.0038)十分接近自由电子的 g 值(2.0023)。 实际上样品是一个含有大量不成对的电子自旋所组成的系统,在 磁场中只分裂为二个塞曼能级。在热平衡时,分布于各塞曼能级上的 粒子数服从波耳兹曼分布,即低能级上的粒子数总比高能级的多一 些,因此,即使粒子数因感应辐射由高能级跃迁到低能级的概率和因 感应吸收由低能级跃迁到高能级的概率相等,但由于低能级的粒子数 比高能级的多,也是感应吸收占优势,从而为观测样品的磁共振吸收 信号提供可能性。随着高低能级上粒子数差的减小,以致趋于零,则观测不到共振现象,即所谓饱 和。但实际上共振现象仍可继续发生,这是弛豫过程在起作用,弛豫过程使整个系统有恢复到玻耳 兹曼分布的趋势,两种作用的综合效应,使自旋系统达到动态平衡,电子自旋共振现象就能维持下 去。 电子自旋共振有两种弛豫过程:自旋—晶格弛豫和自旋—自旋弛豫。电子自旋与晶格交换能量, 使得处在高能级的粒子把一部分能量传给晶格,从而返回低能级,这种作用称为自旋—晶格弛豫, 由自旋—晶格弛豫时间 T1 表征。自旋粒子相互之间交换能量,使它们的旋进相位趋于随机分布,这 种作用称自旋—自旋弛豫,由自旋—自旋弛豫时间用 T2 表征。弛豫过程越快,谱线就越宽。通过测 量谱线半高宽 Δω 可估算自旋—自旋弛豫时间 T2,二者关系为 2 2 T (3-3-10) 本实验中分别用射频法和微波法实现电子自旋共振,两种方法中交变磁场 B1 的频率不同,因而 实验装置有很大差异。射频法电子自旋共振实验中交变磁场 B1 是由射频线圈产生的,频率较低,接 收信号的装置与核磁共振实验类似,采用射频线圈结合振荡电路;微波法电子自旋共振实验中交变 磁场是由微波提供的,频率更高,采微波系统提供交变磁场并接收电子自旋共振信号。 实验 3-3-1 射频电子自旋共振 【实验目的】 1. 理解电子自旋共振的基本原理,掌握射频电子自旋共振的实验方法。 2. 掌握观测射频电子自旋共振信号的实验技术。 3. 测定 DPPH 自由基的 g 因子、共振线宽和弛豫时间 T2。 图 3-3-1 DPPH 的结构
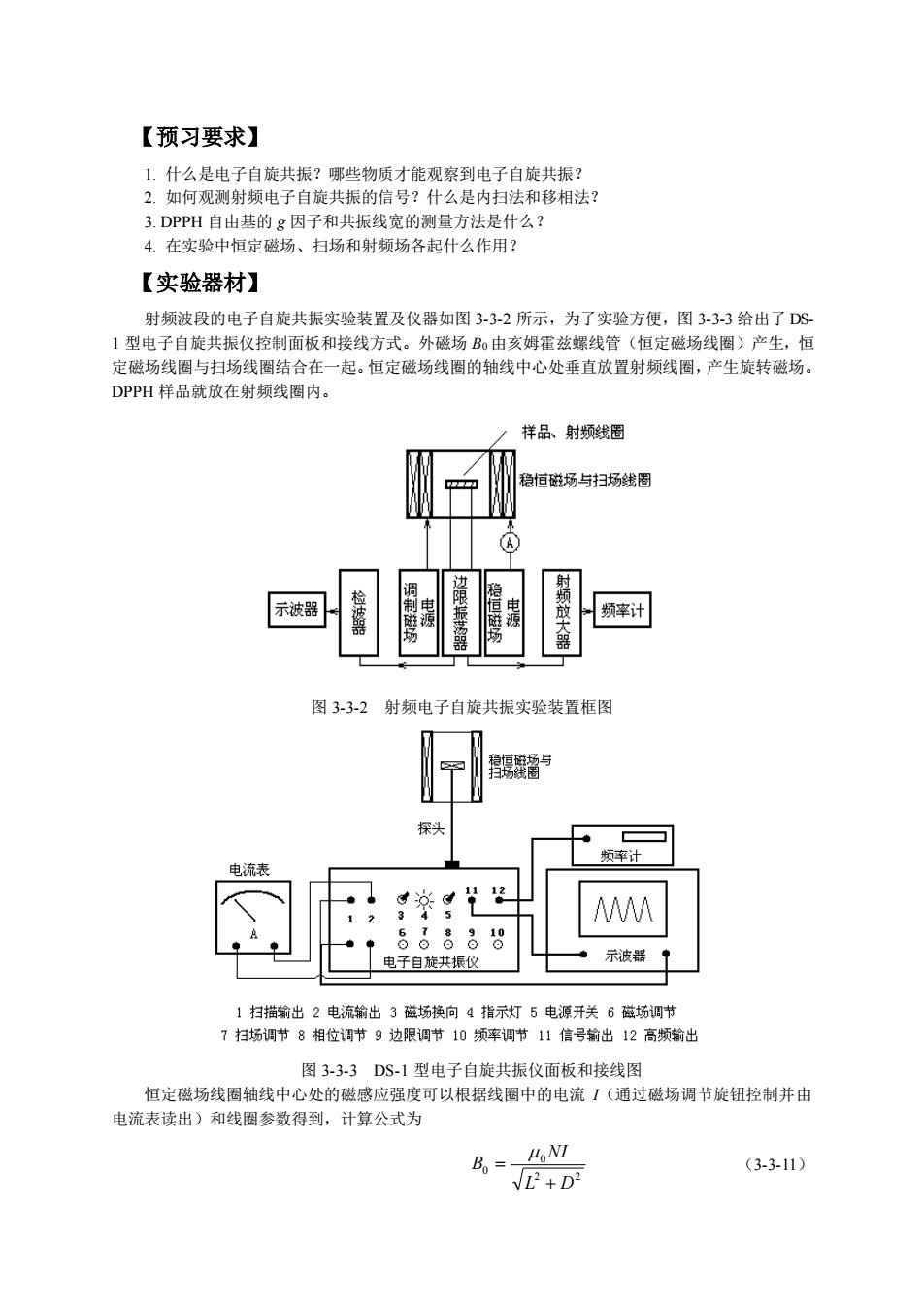
【预习要求】 ,如何观测射频电子自旋共振的信号?什么是内扫法和移相法 3.DPPH自由基的g因子和共振线宽的测量方法是什么? 4.在实验中恒定磁场、扫场和射频场各起什么作用? 【实验器材】 射频波段的电子自旋共振实验装置及仪器如图3-3-2所示, 为了实验方便,图3-3-3给出了DS 1型电子自旋共振仪控制面板和接线方式。外磁场B由亥姆霍兹螺线管(恒定磁场线圆)产生,恒 定磁场线圈与扫场线圈结合在一起。恒定磁场线圈的轴线中心处垂直放置射频线圈,产生旋转磁场。 DPPH样品就放在射频线圈内。 样品、射频线圈 恒磁场与扫场线圈 频率计 图33-2射频电子自旋共振实验装置框图 频车计 电子自旋共振仪 ·示波器中 1扫描输出2电流输出3猫场换向4指示灯5电源开关6磁场调节 7扫场调节8相位调节9边限调节10须率调节11信号输出12高频输出 图3.33DS.1型由子白旋共振仪面板和接线图 恒定磁场线圈轴线中心处的磁感应强度可以根据线圈中的电流(通过磁场调节旋钮控制并由 电流表读出)和线圈参数得到,计算公式为 B。=- (3-3-11 +D
【预习要求】 1. 什么是电子自旋共振?哪些物质才能观察到电子自旋共振? 2. 如何观测射频电子自旋共振的信号?什么是内扫法和移相法? 3. DPPH 自由基的 g 因子和共振线宽的测量方法是什么? 4. 在实验中恒定磁场、扫场和射频场各起什么作用? 【实验器材】 射频波段的电子自旋共振实验装置及仪器如图 3-3-2 所示,为了实验方便,图 3-3-3 给出了 DS- 1 型电子自旋共振仪控制面板和接线方式。外磁场 B0 由亥姆霍兹螺线管(恒定磁场线圈)产生,恒 定磁场线圈与扫场线圈结合在一起。恒定磁场线圈的轴线中心处垂直放置射频线圈,产生旋转磁场。 DPPH 样品就放在射频线圈内。 图 3-3-2 射频电子自旋共振实验装置框图 图 3-3-3 DS-1 型电子自旋共振仪面板和接线图 恒定磁场线圈轴线中心处的磁感应强度可以根据线圈中的电流 I(通过磁场调节旋钮控制并由 电流表读出)和线圈参数得到,计算公式为 2 2 0 0 L D NI B + = (3-3-11)
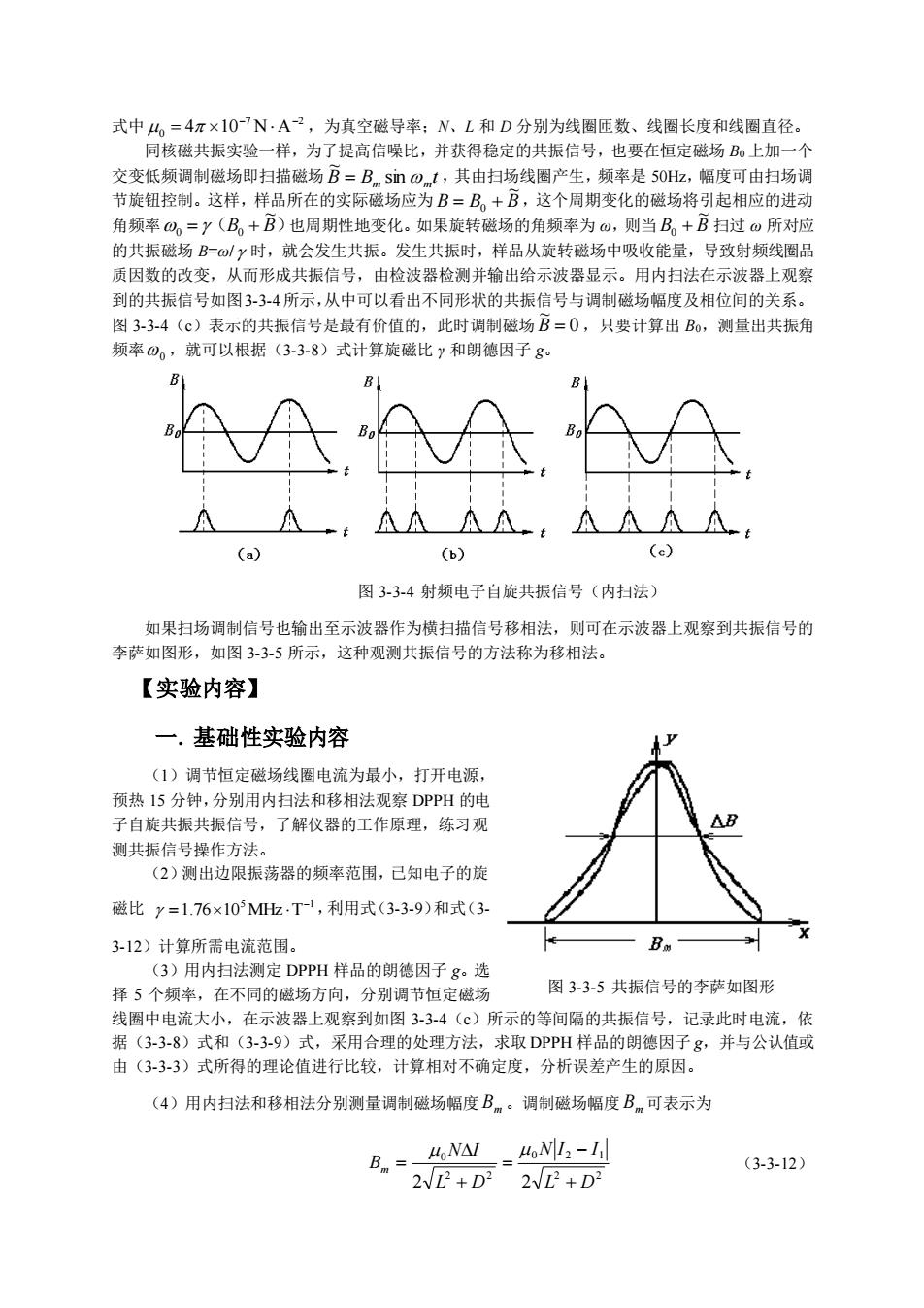
交变低频调制磁场即扫描磁场B=Bsn)1,其由扫场线圈产生,频率是50H,幅度可由扫场调 节旋钮控制。这样,样品所在的实际磁场应为B=B。+B,这个周期变化的磁场将引起相应的进动 角频整)。三y(B。+B)也周期性地变化。加果旋转磁场的角烦整为m,则当B。+B扫过仙所对应 的共银磁场B=时,就会发生共振。发生共振时,样品从旋转磁场中吸收能量,导致射频线圈品 质因数的改变,从而形成共振信号,由检波器检测并输出给示波器显示。用内扫法在示波器上观察 到的共振信号如图3-34所示,从中可以看出不同形状的共振信号与调制磁场幅度及相位间的关系。 图334(©)表示的共振信号是最有价值的,此时调制磁场B=0,只要计算出Ba,测量出共振角 。,就可以根据(3-3-8)式计算旋磁比和朗德因子g。 (a) (b) (c) 图3-34射频电子自旋共振信号(内扫法) 如果扫场调制信号也输出至示波器作为横扫描信号移相法,则可在示波器上观察到共振信号的 李萨如图形,如图33-5所示,这种观测共振信号的方法称为移相法。 【实验内容】 一.基础性实验内容 (1)调节恒定磁场线圈电流为最小,打开电源, 预热15分钟,分别用内扫法和移相法观察DPPH的电 子自旋共振共振信号,了解仪器的工作原理,练习观 测共振信号操作方法 (2)测出边限振荡器的频率范围,已知电子的旋 磁比y=1.76×10M.T-,利用式(3-3-9)和式(3 3-12)计算所需电流范围。 (3)用内扫法测定DPPH样品的朗德因子 图3-3-5共振信号的李萨如图形 线圈中电流大小,在示波器上观察到如图334(c)所示的等间隔的共振信号,记录此时电流,依 据(33-8)式和(33-9)式,采用合理的处理方法,求取DPPH样品的朗德因子g,并与公认值或 由(33-3)式所得的理论值进行比较,计算相对不确定度,分析误差产生的原因。 (4)用内扫法和移相法分别测量调制磁场幅度B。调制磁场幅度B可表示为 B.= (3-3-12) +D
式中 7 2 0 4 10 N A − − = ,为真空磁导率;N、L 和 D 分别为线圈匝数、线圈长度和线圈直径。 同核磁共振实验一样,为了提高信噪比,并获得稳定的共振信号,也要在恒定磁场 B0 上加一个 交变低频调制磁场即扫描磁场 B B t m m sin ~ = ,其由扫场线圈产生,频率是 50Hz,幅度可由扫场调 节旋钮控制。这样,样品所在的实际磁场应为 B B B ~ = 0 + ,这个周期变化的磁场将引起相应的进动 角频率 (B B) ~ 0 = 0 + 也周期性地变化。如果旋转磁场的角频率为 ω,则当 B B ~ 0 + 扫过 ω 所对应 的共振磁场 B=ω/ 时,就会发生共振。发生共振时,样品从旋转磁场中吸收能量,导致射频线圈品 质因数的改变,从而形成共振信号,由检波器检测并输出给示波器显示。用内扫法在示波器上观察 到的共振信号如图3-3-4所示,从中可以看出不同形状的共振信号与调制磁场幅度及相位间的关系。 图 3-3-4(c)表示的共振信号是最有价值的,此时调制磁场 0 ~ B = ,只要计算出 B0,测量出共振角 频率 0 ,就可以根据(3-3-8)式计算旋磁比 γ 和朗德因子 g。 图 3-3-4 射频电子自旋共振信号(内扫法) 如果扫场调制信号也输出至示波器作为横扫描信号移相法,则可在示波器上观察到共振信号的 李萨如图形,如图 3-3-5 所示,这种观测共振信号的方法称为移相法。 【实验内容】 一. 基础性实验内容 (1)调节恒定磁场线圈电流为最小,打开电源, 预热 15 分钟,分别用内扫法和移相法观察 DPPH 的电 子自旋共振共振信号,了解仪器的工作原理,练习观 测共振信号操作方法。 (2)测出边限振荡器的频率范围,已知电子的旋 磁比 5 1 1.76 10 MHz T − = ,利用式(3-3-9)和式(3- 3-12)计算所需电流范围。 (3)用内扫法测定 DPPH 样品的朗德因子 g。选 择 5 个频率,在不同的磁场方向,分别调节恒定磁场 线圈中电流大小,在示波器上观察到如图 3-3-4(c)所示的等间隔的共振信号,记录此时电流,依 据(3-3-8)式和(3-3-9)式,采用合理的处理方法,求取 DPPH 样品的朗德因子 g,并与公认值或 由(3-3-3)式所得的理论值进行比较,计算相对不确定度,分析误差产生的原因。 (4)用内扫法和移相法分别测量调制磁场幅度 Bm 。调制磁场幅度 Bm 可表示为 2 2 0 2 1 2 2 0 2 2 L D N I I L D N I Bm + − = + = (3-3-12) 图 3-3-5 共振信号的李萨如图形

在内扫法中,1对应共振信号刚出现时的恒定磁场线圈电流,即图3-3-4()中各峰刚开始分裂时 对应的恒定磁场线圈电流,而2则对应相邻共振信号合二为一刚消失时的恒定磁场线圈电流。在移 相法中,和h则分别对应于共振信号居于示波器扫描线左端和右端的恒定磁场线圈电流。 (5)用内扫法和移相法分别测量共振谱线宽度△B与横向弛豫时间T,。在内扫法中,共振谱线 宽度△B可表示为 △B=Bnom△t=2πynBn△t (3-3-13) 式中Om、Vm分别为调制磁场的角频率和频率,△1为示波器上用时间表示的共振信号半高宽度。在 移相法中,共振谱线宽度△B可从图3-3-5所示的共振信号中,根据B,按比例直接得到。有了共振 谱线宽度△B,即可得横向弛豫时间T,为 五品 (3-3-14) 二.设计性实验内容 基于本实验的现有条件,设计实验方案,测量地磁场的垂直分量和水平分量。实验要求:阐述 实验基本原理和方法,说明测量系统组成和基本实验步骤,进行实际实验测量,选择合理方法处理 实验数据,分析与讨论实验结果。 【思考与讨论】 1.试阐述电子自旋共振与核磁共振的异同点。 2.简述射频段电子自旋共振的实现方法。 3.为什么在电子自旋共振实验中需要考虑地磁场的影响而核磁共振实验中则不需要考虑? 4.在电子自旋共振实验中如何用移相法测量朗德因子g?
在内扫法中,I1 对应共振信号刚出现时的恒定磁场线圈电流,即图 3-3-4(a)中各峰刚开始分裂时 对应的恒定磁场线圈电流,而 I2 则对应相邻共振信号合二为一刚消失时的恒定磁场线圈电流。在移 相法中,I1 和 I2 则分别对应于共振信号居于示波器扫描线左端和右端的恒定磁场线圈电流。 (5)用内扫法和移相法分别测量共振谱线宽度 B 与横向弛豫时间 T2 。在内扫法中,共振谱线 宽度 B 可表示为 B B t B t = m m = 2 m m (3-3-13) 式中 m、 m 分别为调制磁场的角频率和频率, t 为示波器上用时间表示的共振信号半高宽度。在 移相法中,共振谱线宽度 B 可从图 3-3-5 所示的共振信号中,根据 Bm 按比例直接得到。有了共振 谱线宽度 B ,即可得横向弛豫时间 T2 为 B T = = 2 2 2 (3-3-14) 二. 设计性实验内容 基于本实验的现有条件,设计实验方案,测量地磁场的垂直分量和水平分量。实验要求:阐述 实验基本原理和方法,说明测量系统组成和基本实验步骤,进行实际实验测量,选择合理方法处理 实验数据,分析与讨论实验结果。 【思考与讨论】 1. 试阐述电子自旋共振与核磁共振的异同点。 2. 简述射频段电子自旋共振的实现方法。 3. 为什么在电子自旋共振实验中需要考虑地磁场的影响而核磁共振实验中则不需要考虑? 4. 在电子自旋共振实验中如何用移相法测量朗德因子 g?