
中国石油大学(华东) 近代物理实验 实验5-6康普顿散射实验 刘超卓 理学院物理与光电工程系
刘超卓 理学院 物理与光电工程系 中国石油大学(华东)——近代物理实验 实验5-6 康普顿散射实验

实验背景 1922-1923年间,美国物理学家康普顿研究了X射线被较轻 物质(石墨、石蜡等)散射后光的成分,发现散射谱线中除了 有波长与原波长相同的成分外,还有些波长较长的成分。这种 现象无法用经典电磁理论解释,被称为康普顿散射。 康普顿因发现康普顿散射现象于1927年获诺贝尔物理学奖。 中国赴美留学的吴有训(Y.H.Woo)对康普顿效应的进一步 研究和检验也有很大贡献,有的称这一散射现象为“康普顿 吴有训效应
1922-1923年间,美国物理学家康普顿研究了X射线被较轻 物质(石墨、石蜡等)散射后光的成分,发现散射谱线中除了 有波长与原波长相同的成分外,还有些波长较长的成分。这种 现象无法用经典电磁理论解释,被称为康普顿散射。 康普顿因发现康普顿散射现象于1927年获诺贝尔物理学奖。 中国赴美留学的吴有训(Y. H. Woo)对康普顿效应的进一步 研究和检验也有很大贡献,有的称这一散射现象为“康普顿- 吴有训效应”。 实验背景

实验目的 1.掌握康普顿散射的物理模型,学会康普顿 散射效应的测量技术。 2.通过实验来验证康普顿散射的Y光子能量 及微分散射截面与散射角的关系。 3.了解康普顿散射微分散射截面这一重要概 念,学习测量微分散射截面的实验技术
实验目的 1. 掌握康普顿散射的物理模型,学会康普顿 散射效应的测量技术。 2.通过实验来验证康普顿散射的γ光子能量 及微分散射截面与散射角的关系。 3.了解康普顿散射微分散射截面这一重要概 念,学习测量微分散射截面的实验技术
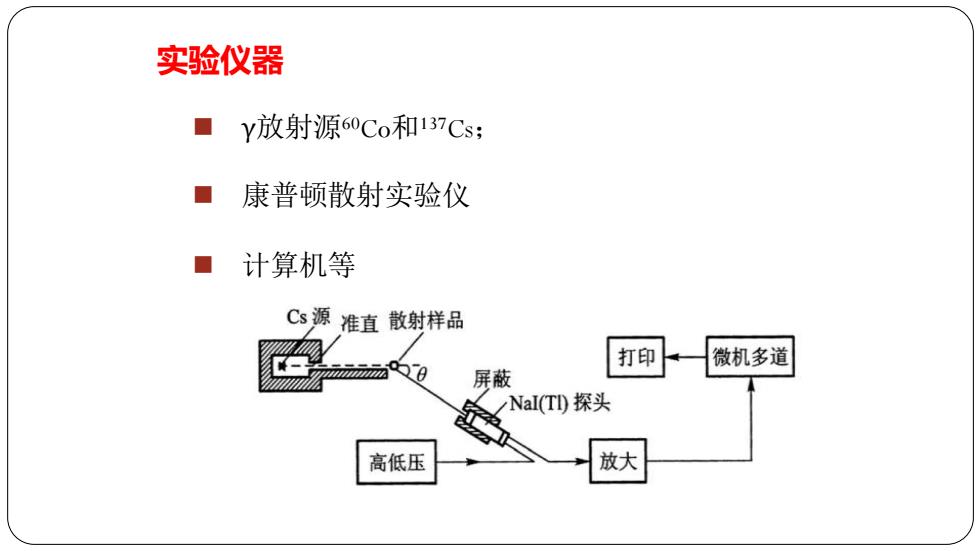
实验仪器 Y放射源60Co和137Cs; 康普顿散射实验仪 计算机等 Cs源准直散射样品 打印 微机多道 屏蔽 NaI(TD探头 高低压 放大
实验仪器 ◼ γ放射源60Co和137Cs; ◼ 康普顿散射实验仪 ◼ 计算机等
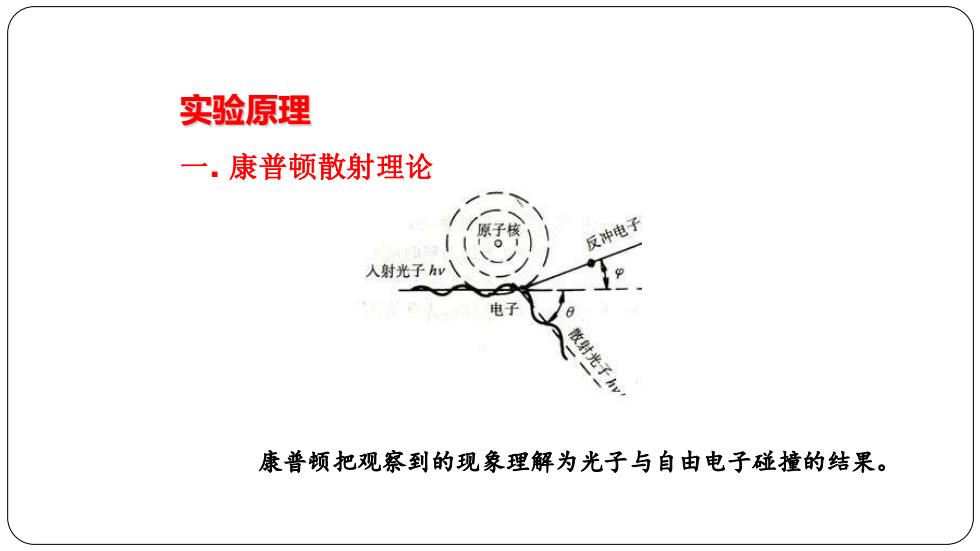
实验原理 一.康普顿散射理论 子 反冲电子 人射光子hv 电子 子hv 康普顿把观察到的现象理解为光子与自由电子碰撞的结果
实验原理 一. 康普顿散射理论 康普顿把观察到的现象理解为光子与自由电子碰撞的结果

体系的能量和动量守恒 hv+Eo=hv'+E p+p-2paPa COs0=p 康普顿散射公式 -元=A2=h1-cos) mc hv 散射光子的能量hw'= 1+y(1-cos8)
2 2 2 0 p p 2p p cos p h E h E + − = + = + (1 cos ) 0 − = = − m c h 体系的能量和动量守恒 散射光子的能量 康普顿散射公式 1 1 cos ( ) h h = + −
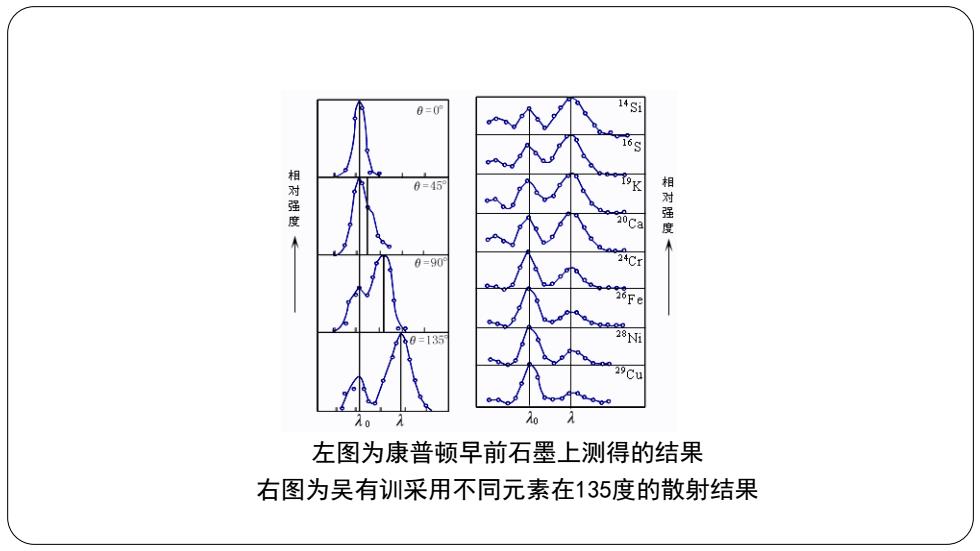
0=0 69 0=45 对强度 相对强度 ,3 Ni Cu 左图为康普顿早前石墨上测得的结果 右图为吴有训采用不同元素在135度的散射结果
左图为康普顿早前石墨上测得的结果 右图为吴有训采用不同元素在135度的散射结果

二,康普顿散射的微分截面 所谓微分散射截面,表示一定能量的入射光子与电子作用 后散射到一定立体角内的几率。 克莱国-科公式贤-如邻+邻n0】 康普顿散射微分截面 d22'c wt-awwoa
二. 康普顿散射的微分截面 所谓微分散射截面,表示一定能量的入射光子与电子作用 后散射到一定立体角内的几率。 克莱因-仁科公式 − + = 2 2 2 sin 2 1 d d h h h h h h rc c ( ) ( ) ( ) 2 2 2 1 1 1 1 cos cos 2 1 1 cos 1 1 cos c c d r d = − + + + − + − d d c 康普顿散射微分截面

9 8 /P/(0)p 0 20 406080100120140160180 137Cs的Y光子散射截面与散射角8之间的关系
137Cs的γ光子散射截面与散射角θ之间的关系

三.微分截面的实验测定 do.(0)1d2 N.(8) N,(e) do.()Id2 R(0)n(0) R(@.)n(@.) 距点源30cmΦ40×40 mmNaI>对点源总探测效率与能量关系 E(MeV) 0.10.150.2 0.30.4 0.5 0.6 0.8 1.0 H0)(10-4)10.910.710.49.178.117.376.87 6.175.69 Φ40×40 mm Nal距点源10cm的峰总比与能量关系 E(MeV) 0.2 0.30.40.5 0.6 0.6620.8 1.0 R(Oθ) 0.88410.72360.58750.49120.42660.39140.33730.2977
三.微分截面的实验测定 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) c p p 0 c 0 0 0 d / d / d / d N N R R = E(MeV) 0.1 0.15 0.2 0.3 0.4 0.5 0.6 0.8 1.0 Η(θ)(10-4)10.9 10.7 10.4 9.17 8.11 7.37 6.87 6.17 5.69 距点源30cm Φ40×40mmNaI对点源总探测效率与能量关系 E(MeV) 0.2 0.3 0.4 0.5 0.6 0.662 0.8 1.0 R(θ) 0.8841 0.7236 0.5875 0.4912 0.4266 0.3914 0.3373 0.2977 Φ40×40mm NaI距点源10cm的峰总比与能量关系