
物理实验教程一近代物理实径nan4 型?为什么? (3)分子动力学模拟计算润湿性接触角的液滴形态法和等密度线拟合法各有什么特 点?试结合模拟结果对比分析哪一种方法计算接触角的误差更小,并说明原因。 (4)在静电场作用下水在SO,表面的润湿性会发生变化吗?试结合模拟计算结果分 析原因。 (5)试结合模拟计算结果分析水和油在SiO2表面的润湿性有何差异,并说明原因。 【参考文献】 [1]刘金远.计算物理学[M们.2版.北京:科学出版社,2022 [2]形辉.计算物理学[M门.北京:科学出版社,2022. [3]安敏荣.分子动力学方法在力学问题中的应用[M们.北京:中国石化出版 社,2020. [4]冯华杰,孙振范.流体分子动力学模拟[们.海口:海南出版社,2015. [5]严六明,朱素华.分子动力学模拟的理论与实践[M门.北京:科学出版社,2013。 [6]SHAFAT MUBIN.JICHIN LI.Extending and Modifying LAMMPS[M].Bir- mingham:Packt Publishing.2021. [7]SUMIT SHARMA.Molecular Dynamics Simulation of Nanocomposites Using BIOVIA Materials Studio,Lammps and Gromacs[M].Amsterdam:Elsevier lnc,2019. [8]MICHAEL P A,DOMINIC J TILDESLEY.Computer Simulation of Liquids [M].Second Edition.Oxford:Oxford University Press,2017 [9]MARK E TUCKERMAN.Statistical Mechanics:Theory and Molecular Sim- ulation[M].Oxford:Oxford University Press.2010. [10]赵明伟,宋旭光,李阳,等,纳米流体改变界而润湿性的综合实验设计[].实验 室研究与探索,2021.40(3):164-166. [11]白清顺,窦昱吴,沈荣琦,等,石墨烯功能表面润湿特性的研究与发展[门,功能 材料.2021.52(10),10029-10038. [12]ALDER BJ.WAINWRIGHT T E.Molecular Dynamies by Electronic Com puters[J].International Symposium on Transport Processes in Statistical Mechanics.1957:97-131. 实验6-5流体流动的格子玻耳兹曼模拟 ● 格子玻耳兹曼方法(LBM)突破了传统计算方法的理论框架,反映出科学研究的一个 基本道理:守恒是物质世界最根本的规律,指导着物质世界的运动和发展:表面对立的双 方存在着一定的内部联系,可通过某种方式达到辩证的统一。与传统计算方法相比,格子 326
— 326 — 型? 为什么? (3)分子动力学模拟计算润湿性接触角的液滴形态法和等密度线拟合法各有什么特 点? 试结合模拟结果对比分析哪一种方法计算接触角的误差更小,并说明原因. (4)在静电场作用下水在SiO2表面的润湿性会发生变化吗? 试结合模拟计算结果分 析原因. (5)试结合模拟计算结果分析水和油在SiO2表面的润湿性有何差异,并说明原因. 【参考文献】 [1] 刘金远.计算物理学[M].2版.北京:科学出版社,2022. [2] 邢辉.计算物理学[M].北京:科学出版社,2022. [3] 安 敏 荣.分 子 动 力 学 方 法 在 力 学 问 题 中 的 应 用 [M].北 京:中 国 石 化 出 版 社,2020. [4] 冯华杰,孙振范.流体分子动力学模拟[M].海口:海南出版社,2015. [5] 严六明,朱素华.分子动力学模拟的理论与实践[M].北京:科学出版社,2013. [6] SHAFAT MUBIN,JICHINLI.ExtendingandModifyingLAMMPS[M].BirG mingham:PacktPublishing,2021. [7] SUMITSHARMA.MolecularDynamicsSimulationofNanocompositesUsing BIOVIA MaterialsStudio,LammpsandGromacs[M].Amsterdam:Elsevier Inc,2019. [8] MICHAELPA,DOMINICJTILDESLEY.ComputerSimulationofLiquids [M].SecondEdition.Oxford:OxfordUniversityPress,2017. [9] MARKETUCKERMAN.StatisticalMechanics:TheoryandMolecularSimG ulation[M].Oxford:OxfordUniversityPress,2010. [10] 赵明伟,宋旭光,李阳,等.纳米流体改变界面润湿性的综合实验设计[J].实验 室研究与探索,2021,40(3):164G166. [11] 白清顺,窦昱昊,沈荣琦,等.石墨烯功能表面润湿特性的研究与发展[J].功能 材料,2021,52(10):10029G10038. [12] ALDERBJ,WAINWRIGHTTE.MolecularDynamicsbyElectronicComG puters[J].InternationalSymposium on TransportProcessesinStatistical Mechanics,1957:97G131. 实验6G5 流体流动的格子玻耳兹曼模拟 格子玻耳兹曼方法(LBM)突破了传统计算方法的理论框架,反映出科学研究的一个 基本道理:守恒是物质世界最根本的规律,指导着物质世界的运动和发展;表面对立的双 方存在着一定的内部联系,可通过某种方式达到辩证的统一.与传统计算方法相比,格子

计算机模拟实验第6章 玻耳兹曼方法的优点主要有:算法简单,即简单的线性运算加上一个松弛 1w 过程就能模拟各种复杂的非线性宏观现象:能够处理复杂的边界条件,可 直接计算有复杂几何边界的问题,无须做计算网格的转换:压力可由状态 方程直接求解:编程容易,计算的前后处理也非常简单:具有很高的并 性。正是由于具有上述优势,格子玻耳兹曼方法自诞生之日起就受到包括 视频41 计 物理学家,数学家、计算机专家和其他领域科学家的广泛关注。在格子玻 方法简 耳兹曼方法的发展过程中,多位中国科学家做出了卓越的贡款。西安交通大学的何雅玲 院士在传热的多尺度数值模拟方面构建了微观-介观-宏观统一计算框架,发展了跨接微 观与宏观的格子玻耳兹曼方法。南方科技大学的单肖文教授提出的Shan-Chen模型被, 泛应用于从燃料电池到宇宙暗能量的多相流动格子破耳薇曼模拟中。上海大学的钱跃站 教授提出了格子玻耳兹曼方法中著名的格子BGK模型DQb,受到国际学术界广泛的关 注,在计算流体力学的基础理论和工业应用上为世界各国科学家所认可并加以推广。 【实验目的】 (1)理解格子玻耳兹曼方法的基本思想,了解中国科学家做出的卓越贡献。 (2)学会格子玻耳兹曼方法的几种常用格子划分和边界条件处理方法。 (3)掌握格子玻耳兹曼方法模拟简单边界条件流体流动的方法 (4)掌握格子玻耳兹曼方法模拟结果的可视化方法。 【预习要求】 (1)什么是格子玻耳兹曼方法? (2)格子玻耳兹曼方法的基本原理是什么? (3)一个完整的格子玻耳兹曼方法由哪三部分组成 (4)速度分布函数f的物理意义是什么? 【实验原理】 一、格子玻耳兹曼方法基本原理 当研究对象的尺度比粒子结构尺度大得多时,连续介质假设就成立, 如飞机在空气中的运动、轮船在水中的运动、血液在动脉中的流动、恒星在 银河系中的运动等,其中空气、水、血液和星系可以看作是连续介质。当粒 子平均自由程和物体特征长度尺度相当时,连续介质假设不能成立,如高 音 真空中的气体分子运动,血液在微血管中的运动等。对于连续介质,使用 视频48 格 Navier-Stokes方程组措述液体的运动是比较方便的,但在某些情况下求 耳兹 万法基本原理 解过程是非常困难或者根本不可能。而对于连续介质假设不能适用或宏 观方程难以描述的系统,采用微观的分子动力学或者介观的气体动理论(gas kinetic theo- y)进行描述更为恰当和可行。但同样面临一些困难,如分子动力学计算量非常大,对于 原子数量多的系统难以完成:气体动理论的基本方程是一个比Navier-Stokes方程组更复 杂的微分方程,求解同样不现实 流体的宏观运动是流体分子微观热运动的统计平均结果,宏观行为对每个具体分子 的运动细节是不敏感的。Navier-Stokes方程组所描述的守恒定律与微观粒子的运动规 327
— 327 — 玻耳兹曼方法的优点主要有:算法简单,即简单的线性运算加上一个松弛 过程就能模拟各种复杂的非线性宏观现象;能够处理复杂的边界条件,可 直接计算有复杂几何边界的问题,无须做计算网格的转换;压力可由状态 方程直接求解;编程容易,计算的前后处理也非常简单;具有很高的并行 性.正是由于具有上述优势,格子玻耳兹曼方法自诞生之日起就受到包括 物理学家、数学家、计算机专家和其他领域科学家的广泛关注.在格子玻 耳兹曼方法的发展过程中,多位中国科学家做出了卓越的贡献.西安交通大学的何雅玲 院士在传热的多尺度数值模拟方面构建了微观G介观G宏观统一计算框架,发展了跨接微 观与宏观的格子玻耳兹曼方法.南方科技大学的单肖文教授提出的ShanGChen模型被广 泛应用于从燃料电池到宇宙暗能量的多相流动格子玻耳兹曼模拟中.上海大学的钱跃竑 教授提出了格子玻耳兹曼方法中著名的格子 BGK 模型 DnQb,受到国际学术界广泛的关 注,在计算流体力学的基础理论和工业应用上为世界各国科学家所认可并加以推广. 【实验目的】 (1)理解格子玻耳兹曼方法的基本思想,了解中国科学家做出的卓越贡献. (2)学会格子玻耳兹曼方法的几种常用格子划分和边界条件处理方法. (3)掌握格子玻耳兹曼方法模拟简单边界条件流体流动的方法. (4)掌握格子玻耳兹曼方法模拟结果的可视化方法. 【预习要求】 (1)什么是格子玻耳兹曼方法? (2)格子玻耳兹曼方法的基本原理是什么? (3)一个完整的格子玻耳兹曼方法由哪三部分组成? (4)速度分布函数f 的物理意义是什么? 【实验原理】 一、格子玻耳兹曼方法基本原理 当研究对象的尺度比粒子结构尺度大得多时,连续介质假设就成立, 如飞机在空气中的运动、轮船在水中的运动、血液在动脉中的流动、恒星在 银河系中的运动等,其中空气、水、血液和星系可以看作是连续介质.当粒 子平均自由程和物体特征长度尺度相当时,连续介质假设不能成立,如高 真空中的气体分子运动、血液在微血管中的运动等.对于连续介质,使用 NavierGStokes方程组描述液体的运动是比较方便的,但在某些情况下求 解过程是非常困难或者根本不可能.而对于连续介质假设不能适用或宏 观方程难以描述的系统,采用微观的分子动力学或者介观的气体动理论(gaskinetictheoG ry)进行描述更为恰当和可行.但同样面临一些困难,如分子动力学计算量非常大,对于 原子数量多的系统难以完成;气体动理论的基本方程是一个比 NavierGStokes方程组更复 杂的微分方程,求解同样不现实. 流体的宏观运动是流体分子微观热运动的统计平均结果,宏观行为对每个具体分子 的运动细节是不敏感的.NavierGStokes方程组所描述的守恒定律与微观粒子的运动规

物理实险教程一近代物理实径S 律是一致的,流体分子内部相互作用的差别反映在Navier-Stokes方程组的输运系数上。 因此,人们可以构造微观或介观模型,使之在遵循基本守恒定律的前提下尽可能地简洁。 格子玻耳兹曼方法就是在此原则上发展起来的。格子玻耳兹曼方法的基本思路是:把系 统划分为网格,相应的时间也划分为离散的步,每个节点包括大量分子(如10°个以上): 每个节点内部的分子发生碰撞,碰撞之后发生迁移,根据之前划分的网格,规定迁移只朝 着特定的儿个方向进行,如二维的只周围八个方向迁移,加上自身不迁移的,共计九个 方向,同时周围八个方向相邻节点上的分子也向该节点迁移。为此,定义速度分布函数 f为: f■f(r.E.t) (6-5-1) 式中,r(xy,x)为空间位置:(,)为分子速度;t为时间。f(r,t)drd表示t时 刻在r到r十dr间的体积元中速度在到十d间的分子数。根据∫的定义有: n(r)=f(r,t)d (6-5-2) 式中,(r)为1时刻r处单位体积内的分子数,也称数密度 格子玻耳兹曼方法基于三个重要假设: (1)分子互相碰撞时只考虑二体碰撞,即认为三个分子或者三个以上分子同时碰撞 在一起的概率很小: (2)分子混沌假设,即认为各个分子的速度分布是独立的,不依赖于另外的分子,也 就是粒子在碰撞之前速度不相关: (3)外力不影响局部碰撞的动力学行为。 根据分子守恒定律可以得到速度分布函数∫的控制方程,也称玻耳兹曼方程 +影+= (6-5-3) 式中为作用于每个分子上的外力项:等号右侧为碰撞项,其表达式极为复杂。因此。 要获得玻耳兹曼方程的解析解一般是不可能的,但单组分单原子气体在不受外力作用的 条件下可以得到玻耳兹曼方程的一个解,即单组分单原子气体的平衡态分布 一麦克斯 韦分布。 为了解决碰撞项的难题,玻耳兹曼提出了H定理,即H函数不会随时间变化而增 长,当时间变化而速度分布函数发生变化时H总是减少的,当H减少到它的极小值而不 再改变时系统就达到了平衡态。H函数的表达式为: H(t)=Inf= (6-5-4) fdg 式中,上标“一”表示统计平均 以上玻耳兹曼方程仍是形式上的,要想实际计算必须用更加简单的形式代替极为复 杂的碰撞项,在这一背景下产生了BGK近似。1954年,巴特纳格尔(P.L.Bhatnagar)、格 罗斯(E,卫.Gross))和克鲁克(M.Krook)提出了BGK近似,用一个简单的算子,代替玻 耳兹曼方程中的碰撞项,经过一系列推导,玻耳兹曼方程可简化为: 328
— 328 — 律是一致的,流体分子内部相互作用的差别反映在 NavierGStokes方程组的输运系数上. 因此,人们可以构造微观或介观模型,使之在遵循基本守恒定律的前提下尽可能地简洁. 格子玻耳兹曼方法就是在此原则上发展起来的.格子玻耳兹曼方法的基本思路是:把系 统划分为网格,相应的时间也划分为离散的步,每个节点包括大量分子(如1010个以上); 每个节点内部的分子发生碰撞,碰撞之后发生迁移,根据之前划分的网格,规定迁移只朝 着特定的几个方向进行,如二维的只朝周围八个方向迁移,加上自身不迁移的,共计九个 方向,同时周围八个方向相邻节点上的分子也向该节点迁移.为此,定义速度分布函数 f 为: f=f(r,ξ,t) (6G5G1) 式中,r(x,y,z)为空间位置;ξ(ξx,ξy,ξz)为分子速度;t为时间.f(r,ξ,t)drdξ表示t时 刻在r 到r+dr 间的体积元中速度在ξ到ξ+dξ间的分子数.根据f 的定义有: n(r)=∫f(r,ξ,t)dξ (6G5G2) 式中,n(r)为t时刻r 处单位体积内的分子数,也称数密度. 格子玻耳兹曼方法基于三个重要假设: (1)分子互相碰撞时只考虑二体碰撞,即认为三个分子或者三个以上分子同时碰撞 在一起的概率很小; (2)分子混沌假设,即认为各个分子的速度分布是独立的,不依赖于另外的分子,也 就是粒子在碰撞之前速度不相关; (3)外力不影响局部碰撞的动力学行为. 根据分子守恒定律可以得到速度分布函数f 的控制方程,也称玻耳兹曼方程: ∂f ∂t +ξ ∂f ∂r +a ∂f ∂ξ = ∂f ∂t æ è ç ö ø ÷ collide (6G5G3) 式中,a ∂f ∂ξ 为作用于每个分子上的外力项;等号右侧为碰撞项,其表达式极为复杂.因此, 要获得玻耳兹曼方程的解析解一般是不可能的,但单组分单原子气体在不受外力作用的 条件下可以得到玻耳兹曼方程的一个解,即单组分单原子气体的平衡态分布———麦克斯 韦分布. 为了解决碰撞项的难题,玻耳兹曼提出了 H 定理,即 H 函数不会随时间变化而增 长,当时间变化而速度分布函数发生变化时 H 总是减少的,当 H 减少到它的极小值而不 再改变时系统就达到了平衡态.H 函数的表达式为: H(t)=lnf=∫flnfdξ ∫fdξ = 1 n∫flnfdξ (6G5G4) 式中,上标“—”表示统计平均. 以上玻耳兹曼方程仍是形式上的,要想实际计算必须用更加简单的形式代替极为复 杂的碰撞项,在这一背景下产生了BGK 近似.1954年,巴特纳格尔(P.L.Bhatnagar)、格 罗斯(E.P.Gross)和克鲁克(M.Krook)提出了BGK 近似,用一个简单的算子Ωf 代替玻 耳兹曼方程中的碰撞项,经过一系列推导,玻耳兹曼方程可简化为:

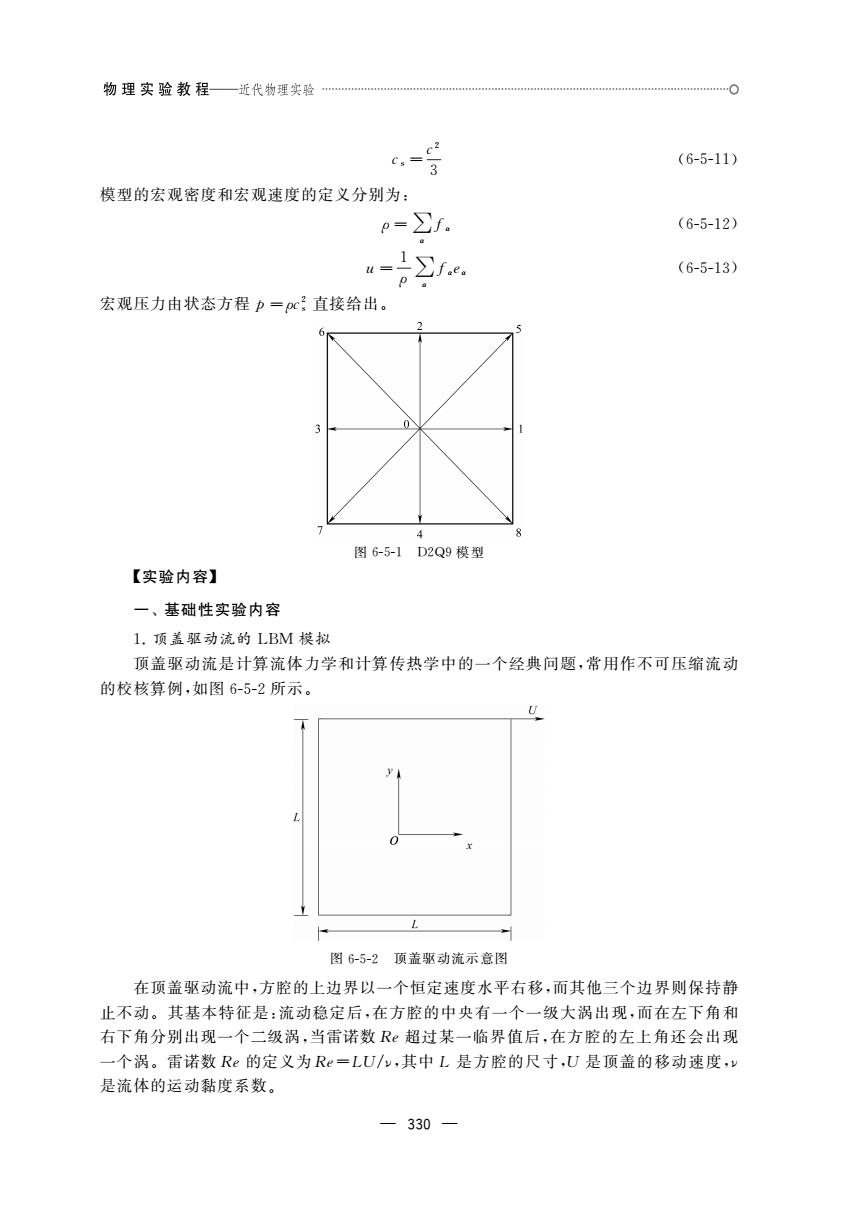
0 计算机模拟实验第6章 影+影+a=m- (6-5-5) 式中,f为平衡态分布函数,可以由麦克斯韦分布导出出为比例系数,其物理意义是在单 位时间内r处一个速度为:的分子与别的分子的碰撞总数,也称碰撞颜率。 格子玻耳兹曼方法是方程(6-5-5)的一种特殊的离散形式,包括速度离散、时间离散 和空间离散。首先要在速度空间对玻耳兹曼方程进行离散。微观粒子无时无刻不在做着 无规则的热运动,因此微观粒子的速度是连续的,其速度在相空间是无穷维的。然而,粒 子的运动细节并不显著决定流体的宏观运动,因此在相空间将粒子的速度:简化为有限 维的速度空间{。,e,.,e、},其中N表示速度的种类数。同时,连续的速度分布函数f 也相应地被离散为{f。,f1,.,f,其中f.=.(r,et),a=0,1,2,.,V。最终得到 离散的玻耳兹曼方程为: f.(r+edt+6,)-f.(r,1)=-[f.(r,t)-f0(r,t)]+6,F.(r,1)(6-5-6) 式中,r为位置,。为速度空间的基,为时间,:为离散的单位时间步,x为弛豫时间,f 为平衡态分布函数,F。为外力。 一个完整的格子玻耳兹曼模型通常由三个部分组成:格子(离散速度模型)、平衡态分 布函数,速度分布函数的演化方程。构造格子玻耳兹曼模型的关键是选择合适的平衡态 分布函数,而平衡态分布函数的具体形式又与离散速度模型的构造有关。离散速度模型 的构造至关重要。如果离散速度的个数太少,则可能导致某些应当守恒的物理量不满足 守恒定律:如果个数太多,则可能造成计算上的浪费。 二、离散速度模型 常用的离散速度模型有二维的D2Q9模型,D2Q7模型,三维的D3Q15模型,D3Q19 模型。 典型的二维速度离散模型一D2Q9模型如图6-5-1所示,不含外力时的玻耳兹曼方 程为 f.+e,04+a)-f.r0=-[.r)-f】 (6-5-7) 速度空间的基为: (0,0), a=0 e。= k(ofa-1v引mfa-v) g=1.2,3,4 (6-5-8) (os[2a-D]sim[2a-D]),e=56,7.8 式中,c=d,/6,6,和8,分别为网格步长和时间步长,且通常有x和y方向的网格步长相 同,即6,=,。平衡态分布函数为: =m+尝+2-周 (6-5-9)】 式中,p为宏观密度,u为宏观速度,c,为格子声速,。为权系数 w=号1=:=a=:=写y=s=@1=,=6 (6-5-10) -329
— 329 — ∂f ∂t +ξ ∂f ∂r +a ∂f ∂ξ =ν(f eq -f) (6G5G5) 式中,f eq为平衡态分布函数,可以由麦克斯韦分布导出;ν为比例系数,其物理意义是在单 位时间内r 处一个速度为ξ的分子与别的分子的碰撞总数,也称碰撞频率. 格子玻耳兹曼方法是方程(6G5G5)的一种特殊的离散形式,包括速度离散、时间离散 和空间离散.首先要在速度空间对玻耳兹曼方程进行离散.微观粒子无时无刻不在做着 无规则的热运动,因此微观粒子的速度是连续的,其速度在相空间是无穷维的.然而,粒 子的运动细节并不显著决定流体的宏观运动,因此在相空间将粒子的速度ξ简化为有限 维的速度空间{e0,e1,,eN },其中 N 表示速度的种类数.同时,连续的速度分布函数f 也相应地被离散为{f0,f1,,fN },其中fα =fα(r,eα,t),α=0,1,2,,N.最终得到 离散的玻耳兹曼方程为: fα(r+eαδt,t+δt)-fα(r,t)=- 1 τ [fα(r,t)-f eq α (r,t)]+δtFα(r,t) (6G5G6) 式中,r 为位置,eα 为速度空间的基,t为时间,δt 为离散的单位时间步,τ 为弛豫时间,f eq α 为平衡态分布函数,Fα 为外力. 一个完整的格子玻耳兹曼模型通常由三个部分组成:格子(离散速度模型)、平衡态分 布函数、速度分布函数的演化方程.构造格子玻耳兹曼模型的关键是选择合适的平衡态 分布函数,而平衡态分布函数的具体形式又与离散速度模型的构造有关.离散速度模型 的构造至关重要.如果离散速度的个数太少,则可能导致某些应当守恒的物理量不满足 守恒定律;如果个数太多,则可能造成计算上的浪费. 二、离散速度模型 常用的离散速度模型有二维的 D2Q9模型、D2Q7模型,三维的 D3Q15模型、D3Q19 模型. 典型的二维速度离散模型———D2Q9模型如图6G5G1所示,不含外力时的玻耳兹曼方 程为: fα(r+eαδt,t+δt)-fα(r,t)=- 1 τ [fα(r,t)-f eq α (r,t)] (6G5G7) 速度空间的基为: eα = (0,0), α=0 ccos (α-1) π 2 é ë ê ê ù û ú ú ,sin (α-1) π 2 é ë ê ê ù û ú ú æ è ç ö ø ÷ , α=1,2,3,4 2ccos (2α-1) π 4 é ë ê ê ù û ú ú ,sin (2α-1) π 4 é ë ê ê ù û ú ú æ è ç ö ø ÷ , α=5,6,7,8 ì î í ï ï ï ï (6G5G8) 式中,c=δx/δt,δx 和δt 分别为网格步长和时间步长,且通常有x 和y 方向的网格步长相 同,即δx =δy.平衡态分布函数为: f eq α =ρωα 1+ eαu c2 s + (eαu)2 2c4 s - u2 2c2 s é ë ê ê ù û ú ú (6G5G9) 式中,ρ为宏观密度,u 为宏观速度,cs 为格子声速,ωα 为权系数. ω0 = 4 9 , ω1 =ω2 =ω3 =ω4 = 1 9 , ω5 =ω6 =ω7 =ω8 = 1 36 (6G5G10)
物理实验教程—近代物理实检O 6-月 (6-5-110 模型的宏观密度和宏观速度的定义分别为: p=∑f (6-5-12) -e. (6-5-13) 宏观压力由状态方程p=Pc:直接给出。 图6-5-1D2Q9模型 【实验内容】 一、基础性实验内容 1.顶盖驱动流的LBM模拟 顶盖驱动流是计算流体力学和计算传热学中的一个经典问题,常用作不可压缩流动 的校核算例,如图6-5-2所示。 图6-5-2顶羞邪动流示意图 在顶盖驱动流中,方腔的上边界以一个恒定速度水平右移,而其他三个边界则保持静 止不动。其基本特征是:流动稳定后,在方腔的中央有一个一级大涡出现,而在左下角和 右下角分别出现一个二级祸,当雷诺数R:超过某一临界值后,在方腔的左上角还会出现 一个涡。雷诺数Re的定义为Re=LU/,其中L是方腔的尺寸,U是顶盖的移动速度,w 是流体的运动黏度系数。 —330
— 330 — cs = c2 3 (6G5G11) 模型的宏观密度和宏观速度的定义分别为: ρ=∑α fα (6G5G12) u= 1 ρ∑α fαeα (6G5G13) 宏观压力由状态方程p=ρc2 s 直接给出. 图6G5G1 D2Q9模型 【实验内容】 一、基础性实验内容 1.顶盖驱动流的 LBM 模拟 顶盖驱动流是计算流体力学和计算传热学中的一个经典问题,常用作不可压缩流动 的校核算例,如图6G5G2所示. 图6G5G2 顶盖驱动流示意图 在顶盖驱动流中,方腔的上边界以一个恒定速度水平右移,而其他三个边界则保持静 止不动.其基本特征是:流动稳定后,在方腔的中央有一个一级大涡出现,而在左下角和 右下角分别出现一个二级涡,当雷诺数Re超过某一临界值后,在方腔的左上角还会出现 一个涡.雷诺数Re的定义为Re=LU/ν,其中L 是方腔的尺寸,U 是顶盖的移动速度,ν 是流体的运动黏度系数

计算机模拟实验第6章 (1)雷诺数分别取400,1000,2000,5000进行模拟计算,分析其对流体运动的影响。 (2)通过改变网格的大小进行多次模拟,分析网格大小对计算结果和计算时间的 影响 2.二维直管内流体流动的LBM模拟 (1)利用LBM模拟二维直管内流体的运动,要求入口处速度恒定,管的长度为宽度 的五倍以上 (2)通过改变二维直管内流体的雷诺数进行多次模拟,分析雷诺数对流体运动的 影响。 (3)分析流体在管内的流动特征。 二、设计性实验内容 (1)在二维直管内设置一个方形或圆形固体障碍物,采用LBM模拟流体的运动过程 并分析流体的运动形态及原因。 (2)假设二维直管内充满原油,从入口处以恒定速度或压力充入水,采用LBM模拟 水驱油过程,观察并分析两种流体的运动形态。 【注意事项】 (1)可自行选择适合自己的程序语言,推荐使用C+十程序。 (2)误差计算应根据雷诺数的不同随时调整收敛判据值。 【思考与讨论】 (1)雷诺数表征的是流体运动的什么性质? (2)网格与计算速度、收敛速度的关系是什么? (3)节点初始化对计算结果有没有影响?为什么? (4)直管流模拟中,如果在出口处设置恒速,对计算结果有没有影响? (5)程序中使用的物理量均为格子单位,应如何转化为实际的物理单位? 【参考文献】 [1]何雅玲,王勇,李庆.格子Boltzmann方法的理论及应用[M们.北京:科学出版 社.2009 [2]郭照立,郑楚光.格子Boltzmann方法的原理及应用[M们.北京:科学出版 社,2009. [3]黄俊涛.格子Boltzmann方法的边界和界面格式[M们.北京:清华大学出版 社,2021. [4]安德里亚·蒙特梭利,贾科莫·法尔库奇。复杂流的格子玻尔兹曼难模的工程 应用[M们.哈尔滨:哈尔滨工业大学出版社,2021. [5]焦魁.多物理场传热传质基础与建模实例[M们.天津:天津大学出版社,2022. -331-
— 331 — (1)雷诺数分别取400,1000,2000,5000进行模拟计算,分析其对流体运动的影响. (2)通过改变网格的大小进行多次模拟,分析网格大小对计算结果和计算时间的 影响. 2.二维直管内流体流动的 LBM 模拟 (1)利用 LBM 模拟二维直管内流体的运动,要求入口处速度恒定,管的长度为宽度 的五倍以上. (2)通过改变二维直管内流体的雷诺数进行多次模拟,分析雷诺数对流体运动的 影响. (3)分析流体在管内的流动特征. 二、设计性实验内容 (1)在二维直管内设置一个方形或圆形固体障碍物,采用 LBM 模拟流体的运动过程 并分析流体的运动形态及原因. (2)假设二维直管内充满原油,从入口处以恒定速度或压力充入水,采用 LBM 模拟 水驱油过程,观察并分析两种流体的运动形态. 【注意事项】 (1)可自行选择适合自己的程序语言,推荐使用 C++程序. (2)误差计算应根据雷诺数的不同随时调整收敛判据值. 【思考与讨论】 (1)雷诺数表征的是流体运动的什么性质? (2)网格与计算速度、收敛速度的关系是什么? (3)节点初始化对计算结果有没有影响? 为什么? (4)直管流模拟中,如果在出口处设置恒速,对计算结果有没有影响? (5)程序中使用的物理量均为格子单位,应如何转化为实际的物理单位? 【参考文献】 [1] 何雅玲,王勇,李庆.格子 Boltzmann方法的理论及应用[M].北京:科学出版 社,2009. [2] 郭照 立,郑 楚 光.格 子 Boltzmann 方 法 的 原 理 及 应 用 [M].北 京:科 学 出 版 社,2009. [3] 黄俊涛.格子 Boltzmann 方法的边界和界面格式[M].北京:清华大学出版 社,2021. [4] 安德里亚蒙特梭利,贾科莫法尔库奇.复杂流的格子玻尔兹曼建模的工程 应用[M].哈尔滨:哈尔滨工业大学出版社,2021. [5] 焦魁.多物理场传热传质基础与建模实例[M].天津:天津大学出版社,2022.