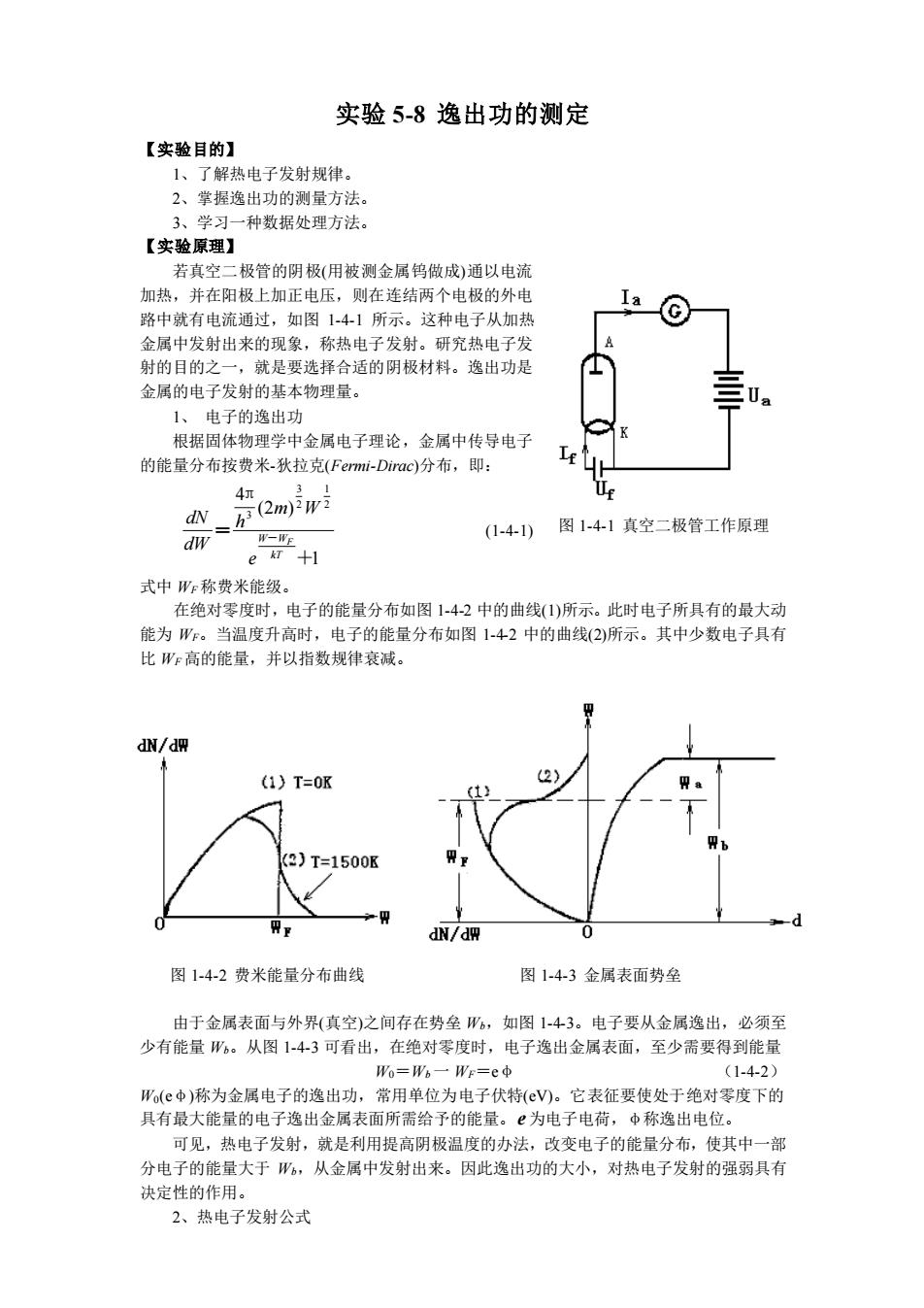
实验5-8逸出功的测定 【实验目的】 1、了解热电子发射规律。 2、掌握逸出功的测量方法。 3、学习一种数据处理方法。 【实验原理】 若真空二极管的阴极(用被测金属钨做成)通以电流 加热,并在阳极上加正电压,则在连结两个电极的外电 路中就有电流通过,如图1-4-1所示。这种电子从加热 金属中发射出来的现象,称热电子发射。研究热电子发 射的目的之一,就是要选择合适的阴极材料。逸出功是 金属的电子发射的基本物理量 1、电子的逸出功 根据固体物理学中金属电子理论,金属中传导电子 的能量分布按费米-狄拉克(Femi-Dirac)分布,即: m 31 (1-4-1) 图1-41真空二极管工作原理 dw W一WF e知+1 式中We称费米能级。 在绝对零度时,电子的能量分布如图14-2中的曲线(1)所示。此时电子所具有的最大动 能为W。当温度升高时,电子的能量分布如图1-42中的曲线(2)所示。其中少数电子具有 比WF高的能量,并以指数规律衰减。 dN/dW (1)T=0K 2) 1) (3)T=1500K 。-d RF dN/dW 图1-4-2费米能量分布曲线 图1-4-3金属表面势垒 由于金属表面与外界(真空)之间存在势垒W6,如图1-43。电子要从金属逸出,必须至 少有能量W6。从图1-43可看出,在绝对零度时,电子逸出金属表面,至少需要得到能量 Wo=W6一Wr=e中 (1-4-2) Wa(e中)称为金属电子的逸出功,常用单位为电子伏特(V)。它表征要使处于绝对零度下的 具有最大能量的电子逸出金属表面所需给予的能量。为电子电荷,中称逸出电位。 可见,热电子发射,就是利用提高阴极温度的办法,改变电子的能量分布,使其中一部 分电子的能量大于W6,从金属中发射出来。因此逸出功的大小,对热电子发射的强弱具有 决定性的作用。 2、热电子发射公式
实验 5-8 逸出功的测定 【实验目的】 1、了解热电子发射规律。 2、掌握逸出功的测量方法。 3、学习一种数据处理方法。 【实验原理】 若真空二极管的阴极(用被测金属钨做成)通以电流 加热,并在阳极上加正电压,则在连结两个电极的外电 路中就有电流通过,如图 1-4-1 所示。这种电子从加热 金属中发射出来的现象,称热电子发射。研究热电子发 射的目的之一,就是要选择合适的阴极材料。逸出功是 金属的电子发射的基本物理量。 1、 电子的逸出功 根据固体物理学中金属电子理论,金属中传导电子 的能量分布按费米-狄拉克(Fermi-Dirac)分布,即: 1 (2 ) 4 2 1 2 3 3 + π = - kT W WF e m W h dW dN (1-4-1) 式中 WF 称费米能级。 在绝对零度时,电子的能量分布如图 1-4-2 中的曲线(1)所示。此时电子所具有的最大动 能为 WF。当温度升高时,电子的能量分布如图 1-4-2 中的曲线(2)所示。其中少数电子具有 比 WF 高的能量,并以指数规律衰减。 由于金属表面与外界(真空)之间存在势垒 Wb,如图 1-4-3。电子要从金属逸出,必须至 少有能量 Wb。从图 1-4-3 可看出,在绝对零度时,电子逸出金属表面,至少需要得到能量 W0=Wb 一 WF=eφ (1-4-2) W0(eφ)称为金属电子的逸出功,常用单位为电子伏特(eV)。它表征要使处于绝对零度下的 具有最大能量的电子逸出金属表面所需给予的能量。 e 为电子电荷,φ称逸出电位。 可见,热电子发射,就是利用提高阴极温度的办法,改变电子的能量分布,使其中一部 分电子的能量大于 Wb,从金属中发射出来。因此逸出功的大小,对热电子发射的强弱具有 决定性的作用。 2、热电子发射公式 图 1-4-1 真空二极管工作原理 图 1-4-2 费米能量分布曲线 图 1-4-3 金属表面势垒

根据费米-狄拉克能量分布公式(141),可以推导出热电子发射公式,称里查逊杜什曼 (Richardson-Dushman)公式。 lo=AST'e i (1-4-3) 式中:热电子发射的电流强度(A) S-阴极金属的有效发射面积(cm2) k玻尔兹曼常数 T绝对温度 中金属的逸出功 A与阴极化学纯度有关的系数 原则上,只要测出6,4,S,了,便可(143)式计算出逸出功©中,但困难的是4和S 是难以直接测量的,所以,在实际测量中,常用下述的里查逊直线法确定©中,以设法避开 A和S的测量。 3、里查逊直线法 将(14-3)式两边除以户,再取对数,得到 g宁=g45-207=6-50x10号 eΦ (1-44) 从14)试可以看出,是与成线性关系。如果以是为飘坐标轴,为横坐标 轴作图。从得到的直线斜率即可求出电子的逸出功c中值:A和S的影响只是使g片一月 直线平移 4、发射电流6的测量 (1-43)式中的。是不存在外电场时的阴极热发射电流。无外场时,电子不断地从阴极发 射出来,在飞向阳极的途中,必然形成空间电荷,空间电荷在阴极附近形成的电场,正好阻 止热电子的发射,这就严重地影响发射电流的测量。为了消除空间电荷的影响,在阳极加 正电压,于是阳极和阴极之间形成一加速电场E,使电子加速飞向阳极。然而由于E的存 在,使阴极发射电子得到助力,发射电流 无电场时大。这一现象称肖特基(Scho内)效应。 根据二极管理论,可以证明,在加速电场E的作用下,阴极发射的电流为 4.39√E I.=Ioexp (1-45) 式中1和6分别是加速电场为E。和零时的阴极发射电流。对(145)式取对数,则 e=十器同 (1-4-6) 考虑到阴极和阳极共轴,且是园柱形,并忽略接触电势差和其它影响,则加速电场可表 示为 E。= U. (1-47) 血3 式中n和n分别为阴极和阳极的半径:U,为阳极电压。将147)式代入(14-6)式,得到
根据费米-狄拉克能量分布公式(1-4-1),可以推导出热电子发射公式,称里查逊-杜什曼 (Richardson-Dushman)公式。 kT e I AST e Φ - = 2 0 (1-4-3) 式中:I0-热电子发射的电流强度(A) S-阴极金属的有效发射面积(cm2 ) k-玻尔兹曼常数 T-绝对温度 eφ-金属的逸出功 A-与阴极化学纯度有关的系数 原则上,只要测出 I0,A,S,T,便可由(1-4-3)式计算出逸出功 eφ,但困难的是 A 和 S 是难以直接测量的,所以,在实际测量中,常用下述的里查逊直线法确定 eφ,以设法避开 A 和 S 的测量。 3、里查逊直线法 将(1-4-3)式两边除以 T 2,再取对数,得到 T lg AS 5.04 10 2.30kT e lg AS T I lg 3 2 0 Φ = - Φ = - (1-4-4) 从(1-4-4)式可以看出, 2 0 lg T I 与 T 1 成线性关系。如果以 2 0 lg T I 为纵坐标轴, T 1 为横坐标 轴作图,从得到的直线斜率即可求出电子的逸出功 eφ值。A 和 S 的影响只是使 2 0 lg T I ― T 1 直线平移。 4、发射电流 I0 的测量 (1-4-3)式中的 I0 是不存在外电场时的阴极热发射电流。无外场时,电子不断地从阴极发 射出来,在飞向阳极的途中,必然形成空间电荷,空间电荷在阴极附近形成的电场,正好阻 止热电子的发射,这就严重地影响发射电流的测量。为了消除空间电荷的影响,在阳极加一 正电压,于是阳极和阴极之间形成一加速电场 Ea,使电子加速飞向阳极。然而由于 Ea 的存 在,使阴极发射电子得到助力,发射电流较无电场时大。这一现象称肖特基(Schottky)效应。 根据二极管理论,可以证明,在加速电场 Ea 的作用下,阴极发射的电流为 T E I I a a 4.39 = 0 exp (1-4-5) 式中 Ia 和 I0 分别是加速电场为 Ea 和零时的阴极发射电流。对(1-4-5)式取对数,则 a Ea T I I 2.30 4.39 lg =lg 0+ (1-4-6) 考虑到阴极和阳极共轴,且是园柱形,并忽略接触电势差和其它影响,则加速电场可表 示为 1 2 1 ln r r r U E a a= (1-4-7) 式中 r1 和 r2 分别为阴极和阳极的半径;Ua 为阳极电压。将(1-4-7)式代入(1-4-6)式,得到

g。=g,+439回 (1-48) 2.307 由(148)式可见,温度T一定时,1g6与√。 成线性关系,如图1-4-4所示。此直线的截距为1go。 lgIad 由此便得到温度为工,电场为零时的发射电流 T 5、温度T的测量 T2 由(1-43)式可知,阴极发射电流与T有关,指 数项中含有工,对发射电流的影响很大。温度测量 1gIo T3 误差对结果影响很大。测量阴极温度的方法虽然不 5 少,但精度都不高。 本实验是以测量加热电流的方 10a 法来确定温度。给阴极通以电流小在产生 量的 图1441gl。一√。关系曲线 同时,阴极还辐射热量。在发热功率和辐射功率达 到平衡时,阴极达到一定的温度。电流与温度T有一定函数关系。有人己对纯钨丝的比加 热电流作过精确的测量。比加热电流为I=√P/R,其中P为长为lcm,直径为1lcm的 阴极(称单位阴极)在一定温度下辐射的功率:R为单位阴极的电阻:表示把单位阴极加 热到一定温度所需的电流,单位为AWcm。对于直径为D的阴极,在一定温度下,加热电流 为1,=D。对于我们所用的真空二极管,其加热电流与温度的关系已测定,见表1一4-1。 表1-4-1标准二极管的加热电流与温度的关系 050Q0 TK1720180018801960204021202200 综上所述,要测定某金属材料的逸出功,应首先将其做成二极管阴极,然后测定加热电 流,查得对应的温度T,再测得阳极电压,和发射电流6的关系,通过数据处理,得到 。,最后用里查逊直线法求得逸出功。 【实验装置】 实验装置(W下一1型)如图1-4-5所示,包括标准二极管,灯丝加热电源,电流表, 高压电源,检流计(微安表)和分流器等 1、标准二极管 ◆4 本实验所用的是一个特殊设计的直热式 A 真空二极管,阴极用纯钨做成,阳极是与阴极 共轴的同筒。为消除阴极的冷瑞效应和电场不 均匀的边缘效应,在阳极两端各装一个保护 环。工作时,保护环与阳极等电势,但其电流 不被测量。 2、灯丝电源是连续可调的低压稳定电源, 供给二极管阴极加热电流小,高压稳压电源, 经分压器分压,提供阳极电压U。 0 灯丝电压 3、微安表(G)用来测量阴极发射电流。 图145实验装置连接图 4、分流器:由于测量中的变化范围较 大,在微安表上并联一个分流器,用来扩大量程。分流器的刻度为1,0.5,0.1,0.05
1 2 1 0 2.30 ln 4.39 lg lg r r T r U I I a a= + (1-4-8) 由(1-4-8)式可见,温度 T 一定时,1g Ia 与 Ua 成线性关系。如图 1-4-4 所示。此直线的截距为 1gI0。 由此便得到温度为 T,电场为零时的发射电流 I0。 5、温度 T 的测量 由(1-4-3)式可知,阴极发射电流与 T 有关,指 数项中含有 T,对发射电流的影响很大。温度测量 误差对结果影响很大。测量阴极温度的方法虽然不 少,但精度都不高。本实验是以测量加热电流的方 法来确定温度。给阴极通以电流 If,在产生热量的 同时,阴极还辐射热量。在发热功率和辐射功率达 到平衡时,阴极达到一定的温度。电流 If 与温度 T 有一定函数关系。有人已对纯钨丝的比加 热电流作过精确的测量。比加热电流为 / / / / f Pf Rf I = ,其中 / Pf 为长为 1cm,直径为 1cm 的 阴极(称单位阴极)在一定温度下辐射的功率; / Rf 为单位阴极的电阻; / f I 表示把单位阴极加 热到一定温度所需的电流,单位为 A/cm。对于直径为 D 的阴极,在一定温度下,加热电流 为 2 3 / I f =I f D 。对于我们所用的真空二极管,其加热电流与温度的关系已测定,见表 1-4-1。 表 1-4-1 标准二极管的加热电流与温度的关系 If/A 0.50 0.55 0.60 0.65 0.70 0.75 0.80 T/K 1720 1800 1880 1960 2040 2120 2200 综上所述,要测定某金属材料的逸出功,应首先将其做成二极管阴极,然后测定加热电 流 If,查得对应的温度 T,再测得阳极电压 Ua 和发射电流 I0 的关系,通过数据处理,得到 I0,最后用里查逊直线法求得逸出功。 【实验装置】 实验装置(WF—1 型)如图 1-4-5 所示,包括标准二极管,灯丝加热电源,电流表, 高压电源,检流计(微安表)和分流器等。 1、标准二极管 本实验所用的是一个特殊设计的直热式 真空二极管,阴极用纯钨做成,阳极是与阴极 共轴的园筒。为消除阴极的冷端效应和电场不 均匀的边缘效应,在阳极两端各装一个保护 环。工作时,保护环与阳极等电势,但其电流 不被测量。 2、灯丝电源是连续可调的低压稳定电源, 供给二极管阴极加热电流 If,高压稳压电源, 经分压器分压,提供阳极电压 Ua。 3、微安表(G)用来测量阴极发射电流 Ia。 4、分流器:由于测量中 Ia 的变化范围较 大,在微安表上并联一个分流器,用来扩大量程。分流器的刻度为 1,0.5,0.1,0.05,. 图 1-4-4 1g Ia— Ua 关系曲线 图 1-4-5 实验装置连接图

等,表示流过微安表的电流为总电流的若干分之一,而被测的总电流为微安表示值的1/0.5, 1/0.1,.倍。 【实验内容】 1、按图1-4-5接好线路,经检查无误后,接通电源予热10分钟。 2、取不同的灯丝电流(即对应于不同的温度TD,从0.50A开始,每隔0.05A测一次。 对每一电流1,测阳极电压为20,30,40,.,120伏时的电流1a。 注意,1不能超过0.80A,以延长二极管寿命。每改变一次电流值,要恒温5发钟,使 阴极达到热平衡。 3、用单对数坐标纸作gl。-√可。直线,求出截距1g6,即求出不同电流下的o,查 出对应的温度T。 4作g。一1 为一子直线。求直线的斜率△(g异y△(宁人计第坞的逸出功e◆。 5、与公认值时e=4.54eV比较,作误差分析。 【思考题】 1、逸出电位与激发电位、电离电位和光电效应实验中的遏止电位有什么区别? 2、为了提高测量精度,实验中应注意什么? 3、里查逊直线法有什么优点?在你以前作过的实验中,有无类似的数据处理方法? 4、为保护二极管不致损坏,应注意什么? 【参考资料】 1、方俊鑫陆栋,固体物理学,上海:上海科学技术出版社,1981 2、刘学懿,阴极电子学,北京:科学出版社,1980 3、B.M.查廖夫,电子管的计算与设计,北京:高等教育出版社,1957
等,表示流过微安表的电流为总电流的若干分之一,而被测的总电流为微安表示值的 1/0.5, 1/0.1,.倍。 【实验内容】 1、按图 1-4-5 接好线路,经检查无误后,接通电源予热 10 分钟。 2、取不同的灯丝电流 If (即对应于不同的温度 T),从 0.50A 开始,每隔 0.05A 测一次。 对每一电流 If,测阳极电压为 20,30,40,.,120 伏时的电流 Ia。 注意,If 不能超过 0.80A,以延长二极管寿命。每改变一次电流值,要恒温 5 发钟,使 阴极达到热平衡。 3、用单对数坐标纸作 lgIa- Ua 直线,求出截距 1g I0,即求出不同电流 If 下的 I0,查 出对应的温度 T。 4、作 2 0 lg T I - T 1 直线。求直线的斜率Δ( 2 0 lg T I )/Δ( T 1 )。计算钨的逸出功 eφ。 5、与公认值时 e=4.54eV 比较,作误差分析。 【思考题】 1、逸出电位与激发电位、电离电位和光电效应实验中的遏止电位有什么区别? 2、为了提高测量精度,实验中应注意什么? 3、里查逊直线法有什么优点?在你以前作过的实验中,有无类似的数据处理方法? 4、为保护二极管不致损坏,应注意什么? 【参考资料】 1、方俊鑫 陆栋,固体物理学,上海:上海科学技术出版社,1981 2、刘学懿,阴极电子学,北京:科学出版社,1980 3、B.M.查廖夫,电子管的计算与设计,北京:高等教育出版社,1957