
材料制备与检测技术实验第4章 [3]康伟芳.自旋阀与多层膜巨磁电阻的特性测量及比较.大学物理,2009,28(7): 45-48】 [4]王晓飞,韩凝,李凯,基于改进巨磁电阻芯片的三维地磁传感器设计.磁性材料及 婴件.2014.45(4),28-31 [5]邹红玉.用巨磁电阻式位置传感器测量材料的杨氏模量.传感器与微系统,2009 28(4):105-107. 实验43压电陶瓷的压电常数测量 1880年法国居里兄弟(P.Curie和」.Curie)发现了电气石的压电效应(piezoelectric effect),从此一种新型的功能材料诞生,至今已有130多年的历史。1947年美国罗伯茨 (S.Roberts)首次制成了压电陶瓷(piezoelectric ceramics)材料钛酸钡(BaTiO,),l955年 美国贾菲(B.Jaf)合成了迄今为止压电性能最好的锆钛酸铅(PZT),其压电常数高达 500pC/N以上,而且性能稳定,从此之后压电陶瓷开始井喷式发展。因为含铅压电陶瓷 有巨大毒性,人们不断探索提高无铅压电陶瓷的性能,直到2004年日本斋藤(Y.Sato)使 用特殊方法制成了铌酸钠钾(KNN)无铅压电陶瓷,才将压电常数提高到416pC/N,由此 开启了无铅压电陶瓷研究的热潮。 具有压电效应的材料称为压电材料,可实现机械能和电能的相互转换。大多数品体 都具有压电效应,但多数晶体的压电效应都十分微弱。随着人们对压电材料研究的深入, 逐渐发现了一些性能优良的压电材料,包括石英品体、压电陶瓷、压电薄膜、压电高分子材 料等。常用的压电材料主要有压电品体和压电陶瓷两大类。压电晶体性能优越,但造价 高昂,一般只应用于军工和航空、航天等高科技领城。压电陶瓷制造工艺简单、成本低,而 且具有较高的力学性能和稳定的压电性能。由压电陶瓷制成的各种压电振子、压电电声 器件、压电超声换能器,压电点火器、压电马达、压电变压器、压电传感器等在信息、激光 导航和生物等高技术领城应用非常广泛。在石油资源探测方面,高端声波测井仪的关键 核心部件是压电换能器,由压电陶瓷制成的声波测井换能器已广泛应用于矿场油田勘探。 评价压电陶瓷质量的核心参数是压电常数,本实验重点学习测量压电常数的原理和 方法。 【实验目的】 ()学习压电材料的基本知识,理解压电效应,掌握测量压电常数的原理和方法 (2)学会迈克尔逊干涉法测量压电陶瓷的压电常数。 【预习要求】 (1)压电效应的原理是什么?什么结构的材料具有压电性? (2)压电品体与压电陶瓷的区别是什么? -161-
— 161 — [3] 康伟芳.自旋阀与多层膜巨磁电阻的特性测量及比较.大学物理,2009,28(7): 45G48. [4] 王晓飞,韩焱,李凯.基于改进巨磁电阻芯片的三维地磁传感器设计.磁性材料及 器件,2014,45(4):28G31. [5] 邹红玉.用巨磁电阻式位置传感器测量材料的杨氏模量.传感器与微系统,2009, 28(4):105G107. 实验4G3 压电陶瓷的压电常数测量 1880年法国居里兄弟(P.Curie和J.Curie)发现了电气石的压电效应(piezoelectric effect),从此一种新型的功能材料诞生,至今已有130多年的历史.1947年美国罗伯茨 (S.Roberts)首次制成了压电陶瓷(piezoelectricceramics)材料钛酸钡(BaTiO3),1955年 美国贾菲(B.Jaffe)合成了迄今为止压电性能最好的锆钛酸铅(PZT),其压电常数高达 500pC/N以上,而且性能稳定,从此之后压电陶瓷开始井喷式发展.因为含铅压电陶瓷 有巨大毒性,人们不断探索提高无铅压电陶瓷的性能,直到2004年日本斋藤(Y.Satio)使 用特殊方法制成了铌酸钠钾(KNN)无铅压电陶瓷,才将压电常数提高到416pC/N,由此 开启了无铅压电陶瓷研究的热潮. 具有压电效应的材料称为压电材料,可实现机械能和电能的相互转换.大多数晶体 都具有压电效应,但多数晶体的压电效应都十分微弱.随着人们对压电材料研究的深入, 逐渐发现了一些性能优良的压电材料,包括石英晶体、压电陶瓷、压电薄膜、压电高分子材 料等.常用的压电材料主要有压电晶体和压电陶瓷两大类.压电晶体性能优越,但造价 高昂,一般只应用于军工和航空、航天等高科技领域.压电陶瓷制造工艺简单、成本低,而 且具有较高的力学性能和稳定的压电性能.由压电陶瓷制成的各种压电振子、压电电声 器件、压电超声换能器、压电点火器、压电马达、压电变压器、压电传感器等在信息、激光、 导航和生物等高技术领域应用非常广泛.在石油资源探测方面,高端声波测井仪的关键 核心部件是压电换能器,由压电陶瓷制成的声波测井换能器已广泛应用于矿场油田勘探. 评价压电陶瓷质量的核心参数是压电常数,本实验重点学习测量压电常数的原理和 方法. 【实验目的】 (1)学习压电材料的基本知识,理解压电效应,掌握测量压电常数的原理和方法. (2)学会迈克尔逊干涉法测量压电陶瓷的压电常数. 【预习要求】 (1)压电效应的原理是什么? 什么结构的材料具有压电性? (2)压电晶体与压电陶瓷的区别是什么?

物理实验教程 一近代物理实稻 ( (3)压电常数的物理意义是什么? (4)压电陶瓷片在电场中的微小形变是如何测量的? 【实验原理】 一、压电陶瓷的极化与压电性 压电陶瓷是一种多晶体,具有类似铁磁性材料磁畴的电畴结构,如图4-3-1所示。在 极化处理之前,这种自发极化的各晶粒内的电畴按任意方向排列,自发极化的作用相互抵 消,压电陶瓷的宏观极化强度为零,因此原始的压电陶瓷呈现各向同性。若在一定温度下 对压电陶瓷做极化处理,则其会出现压电性。所谓极化处理是指在一定温度下以强直流 电场迫使电畴自发极化的方向转到与外加电场方向一致,作规则排列,此时压电陶瓷具有 一定的极化强度:然后使温度冷却,撤去电场,电畴方向基本保持不变,余下很强的剩余极 化电场,压电陶资片的两端出现束鲠电荷.一端为正,另一端为负,此时压电陶资早现压电 性。极化处理的压电陶瓷因束缚电荷的作用在压电陶瓷片的极化两端很快吸附一层来自 外界的白由电荷,这时束缚电荷与自由电荷数值相等、极性相反,故此压电陶瓷片对外不 呈现极性,如图4-3-2所示。因此,具有压电性的压电陶瓷是一种经过极化处理后的人工 多晶铁电体 白由电荷 束缚电荷 化处理 图4-31压电陶瓷的极化过程 4-3-2 压电陶瓷束缚电荷与白由电荷 二、压电陶瓷的正压电效应和逆压电效应 如图4-33所示,如果在压电陶瓷片上加一个与极化方向平行的外力,压电陶瓷片将 产生压缩变形,片内的束缚电荷之间距离变小,电畴发生偏转,极化强度变小,因此吸附在 其表面的白由电荷有一部分被释放而呈现放电现象。当撤去外力时,压电陶瓷片恢复原 状,极化强度增大,因此又吸附一部分自由电荷而呈现充电现象。这种因受力而产生的机 械效应转变为电效应、机械能转变为电能的现象称为压电陶瓷的正压电效应。 正压电效应产生的电荷与外力成正比例关系,即 Q-dnFi (4-3-1) 式中,Q。为电荷:dm为压电应力常量,一般为二阶张量:F,为作用力:下标m和j表示 方向。 图4-33正压电效应 162-
— 162 — (3)压电常数的物理意义是什么? (4)压电陶瓷片在电场中的微小形变是如何测量的? 【实验原理】 一、压电陶瓷的极化与压电性 压电陶瓷是一种多晶体,具有类似铁磁性材料磁畴的电畴结构,如图4G3G1所示.在 极化处理之前,这种自发极化的各晶粒内的电畴按任意方向排列,自发极化的作用相互抵 消,压电陶瓷的宏观极化强度为零,因此原始的压电陶瓷呈现各向同性.若在一定温度下 对压电陶瓷做极化处理,则其会出现压电性.所谓极化处理是指在一定温度下以强直流 电场迫使电畴自发极化的方向转到与外加电场方向一致,作规则排列,此时压电陶瓷具有 一定的极化强度;然后使温度冷却,撤去电场,电畴方向基本保持不变,余下很强的剩余极 化电场,压电陶瓷片的两端出现束缚电荷,一端为正,另一端为负,此时压电陶瓷呈现压电 性.极化处理的压电陶瓷因束缚电荷的作用在压电陶瓷片的极化两端很快吸附一层来自 外界的自由电荷,这时束缚电荷与自由电荷数值相等、极性相反,故此压电陶瓷片对外不 呈现极性,如图4G3G2所示.因此,具有压电性的压电陶瓷是一种经过极化处理后的人工 多晶铁电体. 图4G3G1 压电陶瓷的极化过程 图4G3G2 压电陶瓷束缚电荷与自由电荷 二、压电陶瓷的正压电效应和逆压电效应 如图4G3G3所示,如果在压电陶瓷片上加一个与极化方向平行的外力,压电陶瓷片将 产生压缩变形,片内的束缚电荷之间距离变小,电畴发生偏转,极化强度变小,因此吸附在 其表面的自由电荷有一部分被释放而呈现放电现象.当撤去外力时,压电陶瓷片恢复原 状,极化强度增大,因此又吸附一部分自由电荷而呈现充电现象.这种因受力而产生的机 械效应转变为电效应、机械能转变为电能的现象称为压电陶瓷的正压电效应. 正压电效应产生的电荷与外力成正比例关系,即 Qm =dmjFj (4G3G1) 式中,Qm 为电荷;dmj为压电应力常量,一般为二阶张量;Fj 为作用力;下标 m 和j 表示 方向. 图4G3G3 正压电效应

材料制备与检测技术实验第4章 反之,当对压电材料在极化方向上施加一定电场时,材料将产生压电形变。这是由于 压电材料受电场作用时在品体内部产生了应力(压电应力),通过应力作用产生了压电形 变,当外电场撤去时压电形变随之消失,这种现象称为逆压电效应。逆压电效应满足: Si-diE. (4-3-2) 式中,S,为压电形变:d为压电应变常量,一般为二阶张量:E。为外电场强度;下标i和 n表示方向。 压申效应的可逝性如图4-3-4所示,利用这一特性可 正压电效应 实现机械能与电能的能量相互转换。没有损耗时,该过 机械能 压电介质 电能 程将是完全可逆的,此时正压电效应的压电应力常量与 逆压电效应的压电应变常量互为转置矩阵,即[d] 道压电效应 [d]T。因此,两者通常统称为压电常数,并不加以区 图4-3-4压电效应的可逆性 分。实际上压电陶瓷是有损耗的,一般实验通过逆压电效应测出的压电常数(逆压电常 数)略大于通过正压电效应测出的压电常数(正电压常数)。 三、压电常数的测量原理 压电常数既可通过正压电效应测量,也可通过逆压电效应测量。本实验采用逆压电 效应来测量,即通过施加一个外电场来测量压电陶瓷的相应形变。 根据空间受力不同,压电常数为3×6的二阶张量,即 (4-3-3) du dy da du ds du 对于压电陶瓷,只有经极化处理后才具有压电性,而极化方向通常选:方向,因此18 个分量中只有d是非零的,则式(4-3-2)可以简化为: S:=daE3 (4-3-4) 式(4-3-4)表示在:方向上加一电场后,压电陶瓷片在之方向上产生线性应变,其比 例系数为压电常数d。若式(4-3-4)两边同时乘以压电陶瓷片的厚度t,则可得压电陶瓷 片的厚度变化量(形变量)△和压电陶瓷片两端施加的电压U的关系为: △1=St=dnEt=daU (4-3-5 由式(4-3-5)可知,只要测量出压电陶瓷片的厚度变化量△1就能求出压电常数d。 由于压电常数d:在数值上约为l0-oC/N数量级,因此常用的单位是pC/N或者pm/V。 为了测量如此微小的厚度变化,实验中采用迈克尔逊干涉法测量。图435是迈克尔 逊干涉法的光路原理图。由半导体激光器发出的光经分束镜后被分成两路,反射光射向 平面反射镜M(附压电陶瓷组件),透射光射向平面反射镜M:(固定),两路光分别经M, 和M2反射后,再经分束镜反射和透射后又重新会合,经扩束镜到达自屏,产生干涉圆环 如果压电陶瓷片厚度减小或者增大半个波长,光程差就会减小或者增大一个整波长 对应就会有一个干涉圆环“缩进”中心或者自中心“冒出”。如果压电陶瓷片厚度变化为N 个半波长,即 A-N (4-3-6】 163
— 163 — 反之,当对压电材料在极化方向上施加一定电场时,材料将产生压电形变.这是由于 压电材料受电场作用时在晶体内部产生了应力(压电应力),通过应力作用产生了压电形 变,当外电场撤去时压电形变随之消失,这种现象称为逆压电效应.逆压电效应满足: Si =dinEn (4G3G2) 式中,Si 为压电形变;din 为压电应变常量,一般为二阶张量;En 为外电场强度;下标i和 n 表示方向. 图4G3G4 压电效应的可逆性 压电效应的可逆性如图4G3G4所示,利用这一特性可 实现机械能与电能的能量相互转换.没有损耗时,该过 程将是完全可逆的,此时正压电效应的压电应力常量与 逆压电效应的压电应变常量互为转置矩阵,即[dmj]= [din]T. 因此,两者通常统称为压电常 数,并 不 加 以 区 分.实际上压电陶瓷是有损耗的,一般实验通过逆压电效应测出的压电常数(逆压电常 数)略大于通过正压电效应测出的压电常数(正电压常数). 三、压电常数的测量原理 压电常数既可通过正压电效应测量,也可通过逆压电效应测量.本实验采用逆压电 效应来测量,即通过施加一个外电场来测量压电陶瓷的相应形变. 根据空间受力不同,压电常数为3×6的二阶张量,即 [dmj]=[din]T = d11 d12 d13 d14 d15 d16 d21 d22 d23 d24 d25 d26 d31 d32 d33 d34 d35 d36 é ë ê ê ê ê ù û ú ú ú ú (4G3G3) 对于压电陶瓷,只有经极化处理后才具有压电性,而极化方向通常选z 方向,因此18 个分量中只有d33是非零的,则式(4G3G2)可以简化为: S3 =d33E3 (4G3G4) 式(4G3G4)表示在z 方向上加一电场后,压电陶瓷片在z 方向上产生线性应变,其比 例系数为压电常数d33.若式(4G3G4)两边同时乘以压电陶瓷片的厚度t,则可得压电陶瓷 片的厚度变化量(形变量)Δt和压电陶瓷片两端施加的电压U 的关系为: Δt=S3t=d33E3t=d33U (4G3G5) 由式(4G3G5)可知,只要测量出压电陶瓷片的厚度变化量 Δt就能求出压电常数d33. 由于压电常数d33在数值上约为10-10C/N 数量级,因此常用的单位是pC/N 或者pm/V. 为了测量如此微小的厚度变化,实验中采用迈克尔逊干涉法测量.图4G3G5是迈克尔 逊干涉法的光路原理图.由半导体激光器发出的光经分束镜后被分成两路,反射光射向 平面反射镜 M1(附压电陶瓷组件),透射光射向平面反射镜 M2(固定),两路光分别经 M1 和 M2 反射后,再经分束镜反射和透射后又重新会合,经扩束镜到达白屏,产生干涉圆环. 如果压电陶瓷片厚度减小或者增大半个波长,光程差就会减小或者增大一个整波长, 对应就会有一个干涉圆环“缩进”中心或者自中心“冒出”.如果压电陶瓷片厚度变化为N 个半波长,即 Δt=N λ 2 (4G3G6)
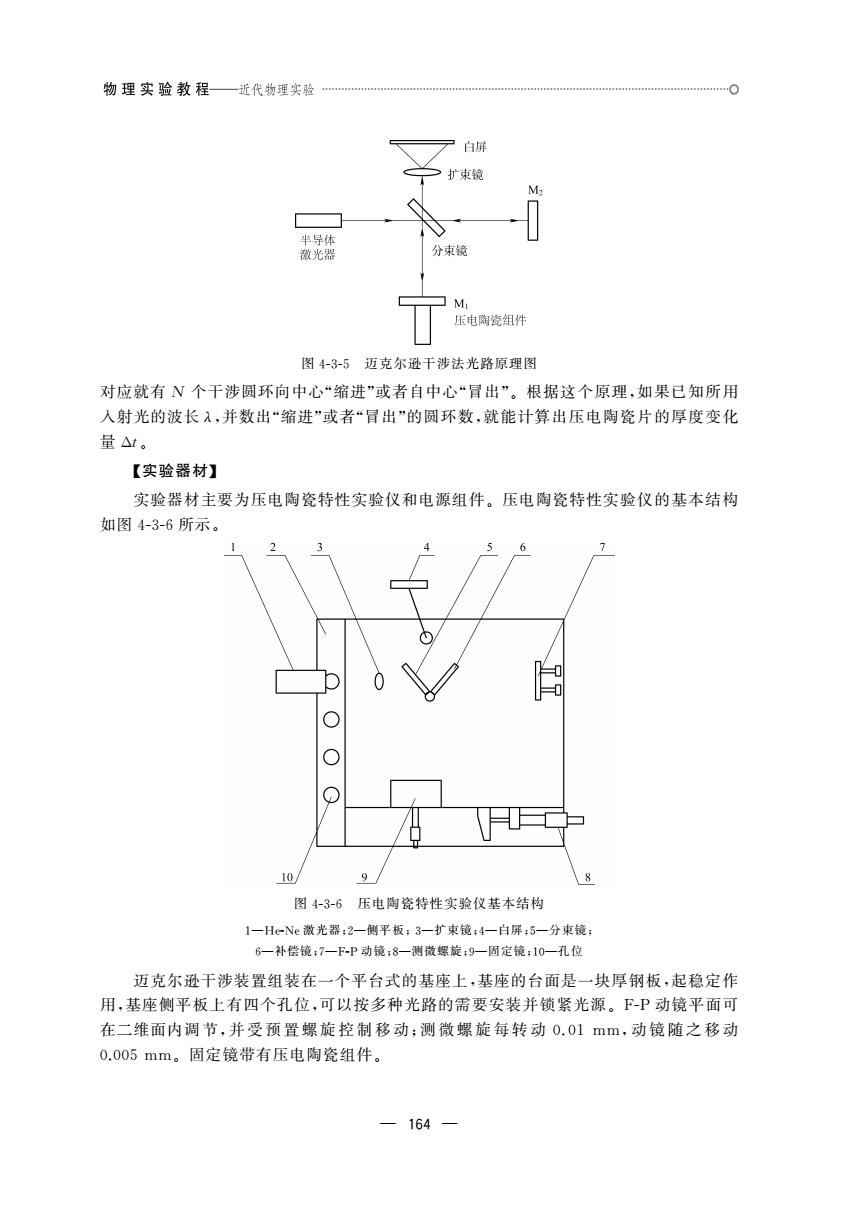
物理实验教程 一近代物理实验 白辩 「束 图4-3-5迈克尔逊干涉法光路原理图 对应就有N个干涉圆环向中心“缩进”或者自中心“冒出”。根据这个原理,如果已知所用 入射光的波长入,并数出“缩进”或者“冒出“的圆环数,就能计算出压电陶瓷片的厚度变化 量△t。 【实验器材】 实验器材主要为压电陶瓷特性实验仪和电源组件。压电陶瓷特性实验仪的基本结构 如图4-3-6所示。 ■ 10/ 图43-6压电陶瓷特性实验仪基本结构 1一HeNe藏光器:2一侧平板:3一扩束镜:4一白屏5一分束镜 6一补偿镜:7一F-P动镜:8一测微螺旋:9一固定镜:10一孔 迈克尔逊干涉装置组装在一个平台式的基座上,基座的台面是一块厚钢板,起稳定作 用,基座侧平板上有四个孔位,可以按多种光路的需要安装并锁紧光源。F-P动镜平面可 在二维面内调节,并受预置螺旋控制移动:测微螺旋每转动0.01mm,动镜随之移动 0.005mm。固定镜带有压电啊瓷组件。 164
— 164 — 图4G3G5 迈克尔逊干涉法光路原理图 对应就有 N 个干涉圆环向中心“缩进”或者自中心“冒出”.根据这个原理,如果已知所用 入射光的波长λ,并数出“缩进”或者“冒出”的圆环数,就能计算出压电陶瓷片的厚度变化 量 Δt. 【实验器材】 实验器材主要为压电陶瓷特性实验仪和电源组件.压电陶瓷特性实验仪的基本结构 如图4G3G6所示. 图4G3G6 压电陶瓷特性实验仪基本结构 1—HeGNe激光器;2—侧平板;3—扩束镜;4—白屏;5—分束镜; 6—补偿镜;7—FGP动镜;8—测微螺旋;9—固定镜;10—孔位 迈克尔逊干涉装置组装在一个平台式的基座上,基座的台面是一块厚钢板,起稳定作 用,基座侧平板上有四个孔位,可以按多种光路的需要安装并锁紧光源.FGP动镜平面可 在二维面内调 节,并 受 预 置 螺 旋 控 制 移 动;测 微 螺 旋 每 转 动 0.01 mm,动 镜 随 之 移 动 0.005mm.固定镜带有压电陶瓷组件

0 材料制各与检测技术实验第4章 【实验内容】 一、基础性实验内容 (1)搭建并调节迈克尔逊干涉仪,观察干涉条纹的形状,并分析干涉条纹的特点。 (2)在干涉条纹出现的条件下接通压电陶瓷电源,使加载在压电陶瓷上的电压U从 0V缓慢加载至150V左右,记录干涉条纹移动的相应数日N,再反方向降压测量,计算 压电常数。实验用的压电陶瓷实际上是压电陶瓷堆,由1O0片小压电陶瓷薄片堆积而成, 故压电常数计算公式为: 1Nλ da-1o02元(am/W (4-3-7】 式中,激光的波长a=632.8nm。 (3)选择电压U为0~150V,每隔15V测一次干涉条纹移动的数目N,绘制电压U 与移动数目V的关系曲线,并根据曲线拟合计算出压电常数d,然后与(2)中的测量结 果进行对比分析。 二、设计性实验内容 试结合现有实验条件通过查阅文献资料自主设计实验方案研究压电陶瓷驱动电压的 频率对压电常数的影响。 实验要求为:阐述实验基本原理和方法,说明测量系统组成和基本实验步骤,进行实 际实验测量,选择合理方法处理实验数据,分析与讨论实验结果。 【注意事项】 (I)HeNe激光器作光源时眼晴不可直视光束。接收并观测激光干涉条纹时必须使 用白玻璃屏,不可用肉眼直接观察,以免伤害视网膜。 (2)压电陶瓷加电后切勿用手去触摸反射镜M,以免发生触电危险 (3)反方向降压测量时要等干涉条纹稳定后再操作。 【思考与讨论】 (1)正压电常数和逆压电常数的物理含义分别是什么? (2)如何测量压电晶体的压电常数? (3)迈克尔逊干涉仪的原理是什么?其干涉图样有什么特点? (4)为什么用迈克尔逊干涉法测量压电陶瓷的压电常数? )用迈克尔逊干涉法测量时,若用黄光或白光代替HeNe激光,干涉图样会有什么 变化? 【参考文献】 [1]王矜奉,苏文斌,王春明,等.压电振动理论与应用.北京:科学出版社,2011 「2门王春雷,幸吉超.赵明磊,笔压由铁电物理北京,科学出版社,2009 [3]张沛林,钟维烈.压电材料与器件物理.济南:山东科学技术出版社,1997 [4]许小红,武海顺.压电薄膜的制备、结构与应用.北京:科学出版社,2002. [5]李书光,王生.物理实验教程 大学物理实验.东营:中国石油大学出版社,2006 165
— 165 — 【实验内容】 一、基础性实验内容 (1)搭建并调节迈克尔逊干涉仪,观察干涉条纹的形状,并分析干涉条纹的特点. (2)在干涉条纹出现的条件下接通压电陶瓷电源,使加载在压电陶瓷上的电压U 从 0V 缓慢加载至150V 左右,记录干涉条纹移动的相应数目 N,再反方向降压测量,计算 压电常数.实验用的压电陶瓷实际上是压电陶瓷堆,由100片小压电陶瓷薄片堆积而成, 故压电常数计算公式为: d33 = 1 100 Nλ 2U (nm/V) (4G3G7) 式中,激光的波长λ=632.8nm. (3)选择电压U 为0~150V,每隔15V 测一次干涉条纹移动的数目 N,绘制电压U 与移动数目N 的关系曲线,并根据曲线拟合计算出压电常数d33,然后与(2)中的测量结 果进行对比分析. 二、设计性实验内容 试结合现有实验条件通过查阅文献资料自主设计实验方案研究压电陶瓷驱动电压的 频率对压电常数的影响. 实验要求为:阐述实验基本原理和方法,说明测量系统组成和基本实验步骤,进行实 际实验测量,选择合理方法处理实验数据,分析与讨论实验结果. 【注意事项】 (1)HeGNe激光器作光源时眼睛不可直视光束.接收并观测激光干涉条纹时必须使 用白玻璃屏,不可用肉眼直接观察,以免伤害视网膜. (2)压电陶瓷加电后切勿用手去触摸反射镜 M1,以免发生触电危险. (3)反方向降压测量时要等干涉条纹稳定后再操作. 【思考与讨论】 (1)正压电常数和逆压电常数的物理含义分别是什么? (2)如何测量压电晶体的压电常数? (3)迈克尔逊干涉仪的原理是什么? 其干涉图样有什么特点? (4)为什么用迈克尔逊干涉法测量压电陶瓷的压电常数? (5)用迈克尔逊干涉法测量时,若用黄光或白光代替 HeGNe激光,干涉图样会有什么 变化? 【参考文献】 [1] 王矜奉,苏文斌,王春明,等.压电振动理论与应用.北京:科学出版社,2011. [2] 王春雷,李吉超,赵明磊,等.压电铁电物理.北京:科学出版社,2009. [3] 张沛林,钟维烈.压电材料与器件物理.济南:山东科学技术出版社,1997. [4] 许小红,武海顺.压电薄膜的制备、结构与应用.北京:科学出版社,2002. [5] 李书光,王殿生.物理实验教程———大学物理实验.东营:中国石油大学出版社,2006.