
光学测量技术实验第1章 2.设计性实验内容 根据现有实验条件,设计实验方案探索分析乙醇汽油溶液的浓度与吸光度的关系。 实验要求为:闸述实验基本原理和方法,说明测量系统组成和基本实验步骤,进行实 际实验测量,选择合理方法处理实验数据,分析与讨论实验结果。 【注意事项】 (1)光栅光谱仪属于贵重精密仪器,超出说明书使用操作时需在教师指导下进行。 (2)狭缝宽度的调节必须小心,且狭缝的宽度不得超过3mm,也不得完全闭合,以免 损坏刀口。实验完毕后,应将狭缝宽度调节到0.2mm左右。 (3)在测量吸收曲线或吸光度-介质厚度关系曲线时,要保证仪器各参数(如狭缝宽 度、光电倍增管工作电压等)不变。 (4)光电倍增管受强光照射时会引发“雪崩效应”,测量时入射光不能太强。 【思考与讨论】 (1)光枥光谱仪波长示值的校准为什么要用汞灯?吸收曲线的测量为什么要用溴 钨灯? (2)试讨论陕缝宽度对测量的影响 (3)吸收光谱和发射光谱的关系是什么? (4)如何测量吸光度? 【参考文献】 [1]邓勃,李玉珍,刘明钟.实用原子光谱分析.北京:化学工业出版社,2013. 「2门杨春昆,幸国华,徐秋心.原子光普分析北京:化学工业出版社,2010 [3]王秉超.大学物理实验(下册).北京:高等教育出版社,2003】 实验1-3超声光栅测量液体中的声速 1932年,美国德拜(P.J.W.Debye)和席尔斯(.W.Sears)以及法国卢卡斯(R.Lu cas)和比卡尔(P.Biquand)分别独立地观察到光在超声波传播的液体中的衍射现象,后来 人们在超声波传插的透明固体中也发现了光衍射现象,这种现象称为声光效应(acouste0 optic effect)。声光效应一般是指光通过受到超声波扰动的介质时发生衍射的现象。20 世纪60年代激光的问世促进了声光效应理论和应用研究的迅速发展,声光效应为控制激 光的频率、方向和强度提供了一种有效的手段,大大扩展了激光的应用领域。利用声光效 应制成的声光器件(acousto-optic devices)如声光调制器、声光可调谐滤器、声光偏转器 等,在激光技术、光信号处理和集成光通信技术等方面有着重要的应用。声光效应还有许 多其他重要应用,如声光频谱分析器和声光信号相关器早已在射电望远镜和微被雷达信 号处理中得到广泛应用,利用声光效应可以探测材料声学性质等。 11
— 11 — 2.设计性实验内容 根据现有实验条件,设计实验方案探索分析乙醇汽油溶液的浓度与吸光度的关系. 实验要求为:阐述实验基本原理和方法,说明测量系统组成和基本实验步骤,进行实 际实验测量,选择合理方法处理实验数据,分析与讨论实验结果. 【注意事项】 (1)光栅光谱仪属于贵重精密仪器,超出说明书使用操作时需在教师指导下进行. (2)狭缝宽度的调节必须小心,且狭缝的宽度不得超过3mm,也不得完全闭合,以免 损坏刀口.实验完毕后,应将狭缝宽度调节到0.2mm 左右. (3)在测量吸收曲线或吸光度G介质厚度关系曲线时,要保证仪器各参数(如狭缝宽 度、光电倍增管工作电压等)不变. (4)光电倍增管受强光照射时会引发“雪崩效应”,测量时入射光不能太强. 【思考与讨论】 (1)光栅光谱仪波长示值的校准为什么要用汞灯? 吸收曲线的测量为什么要用溴 钨灯? (2)试讨论狭缝宽度对测量的影响. (3)吸收光谱和发射光谱的关系是什么? (4)如何测量吸光度? 【参考文献】 [1] 邓勃,李玉珍,刘明钟.实用原子光谱分析.北京:化学工业出版社,2013. [2] 杨春晟,李国华,徐秋心.原子光谱分析.北京:化学工业出版社,2010. [3] 王秉超.大学物理实验(下册).北京:高等教育出版社,2003. 实验1G3 超声光栅测量液体中的声速 1932年,美国德拜(P.J.W.Debye)和席尔斯(F.W.Sears)以及法国卢卡斯(R.LuG cas)和比卡尔(P.Biquand)分别独立地观察到光在超声波传播的液体中的衍射现象,后来 人们在超声波传播的透明固体中也发现了光衍射现象,这种现象称为声光效应(acoustoG opticeffect).声光效应一般是指光通过受到超声波扰动的介质时发生衍射的现象.20 世纪60 年代激光的问世促进了声光效应理论和应用研究的迅速发展,声光效应为控制激 光的频率、方向和强度提供了一种有效的手段,大大扩展了激光的应用领域.利用声光效 应制成的声光器件(acoustoGopticdevices)如声光调制器、声光可调谐滤器、声光偏转器 等,在激光技术、光信号处理和集成光通信技术等方面有着重要的应用.声光效应还有许 多其他重要应用,如声光频谱分析器和声光信号相关器早已在射电望远镜和微波雷达信 号处理中得到广泛应用,利用声光效应可以探测材料声学性质等

物理实验教程一近代物理实检 本实验学习声光效应和超声光栅(ultrasonic grating)的基本原理,观察和分析钠黄光 通过超声光栅后的衍射现象,掌握用超声光栅测量透明液体中的声速(acoustic velocity) 的实验方法。 【实验目的】 (1)理解招声光棚的基本原理,学会观测液体中超声光挪的行射现象 (2)掌握超声光栅测量透明液体中声速的原理、方法和实验技术。 (3)了解产生超声波的方法。 【预习要求】 (1)什么是超声光栅? (2)如何调整分光计才能看到衍射条纹? (3)如何利用超声光栅测量液体中的声速 【实验原理】 一、超声光栅的形成原理 超声波是一种机械应力波。当超声波在液体中传插时,液体会周期性地被压缩或膨 胀,使液体的密度发生周期性的变化。压缩作用会使液体的局部密度变大,膨胀作用会使 液体的局部密度变小,液体局部密度的周期性变化会导致液体折射率的周期性变化。 当光波垂直于超声波传播方向通过液体时,不同位置的光波经历的光程不同。原米 是平面被的光波经过液体后,平面波变为弯曲的非平面波,与相位光栅对光的作用相类 似,如图1-3-1所示(图中4为超声波波长)。这种有超声波场的液体称为超声光橱(超声 相位光栅)。光波通过超声光栅时也会发生光栅衍射现象,称为声光衍射(acousto-optic diffraction)。声光衍射是光波与液体中超声波相互作用的结果。 超声波传播方向 质点稀疏区 平面光被之 质点密集区 图1-3-1超声光栅原理示意图 超声行波形成的超声相位光栅,其栅面在空间是随时间移动的。如果超声波在一个 矩形的玻璃液槽中传播,则从液槽的一个平面传播到另一个平面会被反射而沿反方向传 播,人射波和反射波在液体中叠加而形成驻波。在某一时刻,驻波的任一波节两边的质点 都涌向这个节点,使该节点附近形成质点密集区,而相邻的波节处为质点稀疏区:半个周 12
— 12 — 本实验学习声光效应和超声光栅(ultrasonicgrating)的基本原理,观察和分析钠黄光 通过超声光栅后的衍射现象,掌握用超声光栅测量透明液体中的声速(acousticvelocity) 的实验方法. 【实验目的】 (1)理解超声光栅的基本原理,学会观测液体中超声光栅的衍射现象. (2)掌握超声光栅测量透明液体中声速的原理、方法和实验技术. (3)了解产生超声波的方法. 【预习要求】 (1)什么是超声光栅? (2)如何调整分光计才能看到衍射条纹? (3)如何利用超声光栅测量液体中的声速? 【实验原理】 一、超声光栅的形成原理 超声波是一种机械应力波.当超声波在液体中传播时,液体会周期性地被压缩或膨 胀,使液体的密度发生周期性的变化.压缩作用会使液体的局部密度变大,膨胀作用会使 液体的局部密度变小,液体局部密度的周期性变化会导致液体折射率的周期性变化. 当光波垂直于超声波传播方向通过液体时,不同位置的光波经历的光程不同.原来 是平面波的光波经过液体后,平面波变为弯曲的非平面波,与相位光栅对光的作用相类 似,如图1G3G1所示(图中Λ 为超声波波长).这种有超声波场的液体称为超声光栅(超声 相位光栅).光波通过超声光栅时也会发生光栅衍射现象,称为声光衍射(acoustoGoptic diffraction).声光衍射是光波与液体中超声波相互作用的结果. 图1G3G1 超声光栅原理示意图 超声行波形成的超声相位光栅,其栅面在空间是随时间移动的.如果超声波在一个 矩形的玻璃液槽中传播,则从液槽的一个平面传播到另一个平面会被反射而沿反方向传 播,入射波和反射波在液体中叠加而形成驻波.在某一时刻,驻波的任一波节两边的质点 都涌向这个节点,使该节点附近形成质点密集区,而相邻的波节处为质点稀疏区;半个周
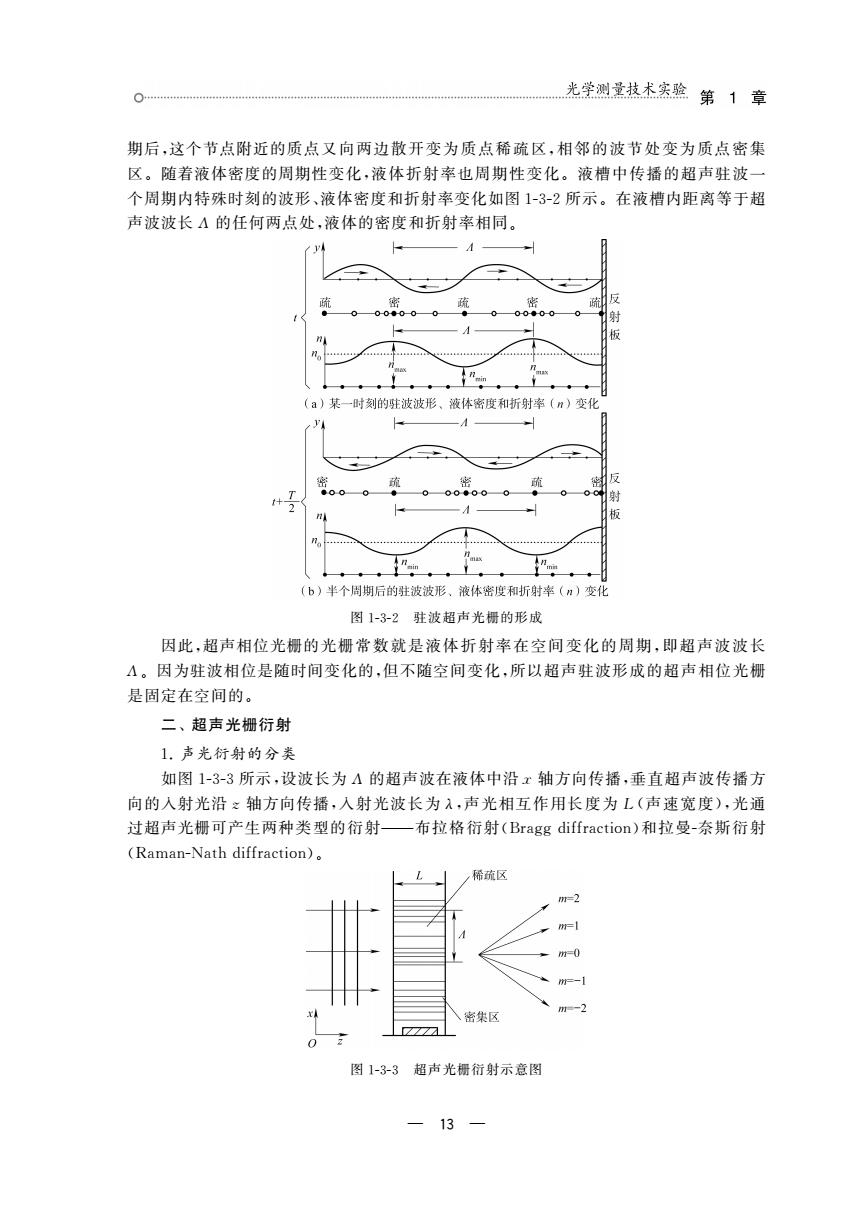
0 光学测量技术实验第1章 期后,这个节点附近的质点又向两边散开变为质点稀疏区,相邻的波节处变为质点密集 区。随着液体密度的周期性变化,液体折射率也周期性变化。液槽中传播的超声驻波一 个周期内特殊时刻的波形、液体密度和折射率变化如图1-32所示。在液槽内距离等于超 声波波长A的任何两点处,液体的密度和折射率相同。 /y4 A 。 (a)某一时刻的班波波形、液体密度和折射率(用)变化 。整。米。一。 ® (b 半个周期后的驻波波形。液体密度折射率()空化 图1-32驻波超声光栅的形成 因此,超声相位光栅的光栅常数就是液体折射率在空间变化的周期,即超声波波长 A。因为驻波相位是随时间变化的,但不随空间变化,所以超声驻波形成的超声相位光栅 是固定在空间的。 二、超声光栅衍射 L.声光衍射的分类 如图1-3-3所示,设波长为A的超声波在液体中沿x轴方向传播,垂直超声波传播方 向的入射光沿:轴方向传播,人射光波长为入,声光相互作用长度为L(声速宽度),光通 过超声光栅可产生两种类型的衍射 -布拉格衍射(Bragg diffraction)和拉曼-奈斯衍射 (Raman-Nath diffraction) 稀流区 图1-3-3超声光栅行射示意图 13
— 13 — 期后,这个节点附近的质点又向两边散开变为质点稀疏区,相邻的波节处变为质点密集 区.随着液体密度的周期性变化,液体折射率也周期性变化.液槽中传播的超声驻波一 个周期内特殊时刻的波形、液体密度和折射率变化如图1G3G2所示.在液槽内距离等于超 声波波长Λ 的任何两点处,液体的密度和折射率相同. 图1G3G2 驻波超声光栅的形成 因此,超声相位光栅的光栅常数就是液体折射率在空间变化的周期,即超声波波长 Λ.因为驻波相位是随时间变化的,但不随空间变化,所以超声驻波形成的超声相位光栅 是固定在空间的. 二、超声光栅衍射 1.声光衍射的分类 如图1G3G3所示,设波长为Λ 的超声波在液体中沿x 轴方向传播,垂直超声波传播方 向的入射光沿z 轴方向传播,入射光波长为λ,声光相互作用长度为L(声速宽度),光通 过超声光栅可产生两种类型的衍射———布拉格衍射(Braggdiffraction)和拉曼G奈斯衍射 (RamanGNathdiffraction). 图1G3G3 超声光栅衍射示意图

物理实验教程一近代物理失检O ①)当超声波颜率较高、声光相互作用长度较大,满足上→会时,产生布拉格行射。 声光介质相当于一个体光棚,衍射光一般只会产生满足布拉格公式的零级和一级衍射极 大值,且土1级衍射极大值不同时存在。 (②)当超声波颜率较低,声光相互作用长度较小,满足L《时,产生拉曼奈斯衍 射。声光介质相当于一个平面光栅,衍射光一般会产生对称于零级的多级衍射极大值,与 平面光栅的衍射类似。 2.拉曼-奈斯衍射 实验中产生的声光衍射类型为拉曼-奈斯衍射。如图1-3-3所示,设频常为f的超声 波引起液体折射率的周期性变化可表示为: nc,)=-ain2xf-) (1-3-1) 式中,。为液体原来的折射率:△为相对于。的折射率最大变化量。考虑到光在液体 中的传插速度(约10m/s)远大于声波的传播速度(约10m/s),可以认为在液体中由超 声波所形成的疏密周期性分布在光波通过液体的这段时间内是不随时间改变的,因此液 体的折射率仅随位置x而改变,则有: nax)-dsin(经) (1-3-2) 若在超声光栅的入射面上的平行光在时刻的波函数为 y-Aexp(2 (1-3-3) 则光通过厚度为L的液体到达超声光栅出射面时的波函数为: y=Aex即2对片-兴月 (1-3-4) 式中,A为振幅:j为虚数单位:T为周期。将式(1-3-2)代入式(1-3-4)可得: y=Aep2号-+兴ne]} (1-3-5) 若令A'=Aex知-2对”的)则式1-35)变为: y-A'expin] (1-3-6) 根据惠更斯-非涅耳原理,超声光栅出射面上的各点可看作一子光源,衍射角为0。的 衍射光到达屏幕上某点时的振幅A可表示为: A-e+nea (1-3-7) 式中,为沿x轴方向超声光橱的宽度:6为衍射光相对于x轴的方向余弦,即 a=cos(7-)=sin0 (1-3-8) 14
— 14 — (1)当超声波频率较高、声光相互作用长度较大,满足L ≫ Λ2 2πλ 时,产生布拉格衍射. 声光介质相当于一个体光栅,衍射光一般只会产生满足布拉格公式的零级和一级衍射极 大值,且±1级衍射极大值不同时存在. (2)当超声波频率较低、声光相互作用长度较小,满足L ≪ Λ2 2πλ 时,产生拉曼G奈斯衍 射.声光介质相当于一个平面光栅,衍射光一般会产生对称于零级的多级衍射极大值,与 平面光栅的衍射类似. 2.拉曼G奈斯衍射 实验中产生的声光衍射类型为拉曼G奈斯衍射.如图1G3G3所示,设频率为f 的超声 波引起液体折射率的周期性变化可表示为: n(x,t)=n0 -Δnsin(2πft- 2π Λ x) (1G3G1) 式中,n0 为液体原来的折射率;Δn 为相对于n0 的折射率最大变化量.考虑到光在液体 中的传播速度(约108 m/s)远大于声波的传播速度(约103 m/s),可以认为在液体中由超 声波所形成的疏密周期性分布在光波通过液体的这段时间内是不随时间改变的,因此液 体的折射率仅随位置x 而改变,则有: n(x)=n0 -Δnsin( 2π Λ x) (1G3G2) 若在超声光栅的入射面上的平行光在t时刻的波函数为: y=Aexp(2πj t T ) (1G3G3) 则光通过厚度为L 的液体到达超声光栅出射面时的波函数为: y=Aexp 2πj( t T - n λ L) é ë ê ê ù û ú ú (1G3G4) 式中,A 为振幅;j为虚数单位;T 为周期.将式(1G3G2)代入式(1G3G4)可得: y=Aexp{2πj t T - n0L λ + ΔnL λ sin(2π x Λ ) é ë ê ê ù û ú ú } (1G3G5) 若令A′=Aexp(-2πj n0L λ ) ,则式(1G3G5)变为: y=A′exp{2πj t T + ΔnL λ sin(2π x Λ ) é ë ê ê ù û ú ú } (1G3G6) 根据惠更斯G菲涅耳原理,超声光栅出射面上的各点可看作一子光源,衍射角为θk 的 衍射光到达屏幕上某点时的振幅AS 可表示为: AS =∫ a 2 - a 2 A′exp{2πj xδ λ + ΔnL λ sin(2π x Λ ) é ë ê ê ù û ú ú }dx (1G3G7) 式中,a 为沿x 轴方向超声光栅的宽度;δ 为衍射光相对于x 轴的方向余弦,即 δ=cos( π 2 -θk ) =sinθk (1G3G8)

光学测量技术实验第1章 再令 “=贸 (1-3-9 0-2x4L (1-3-10) 6- (1-3-11) 则式(1-3-7)可简化为: A.-A'expfj[ur+vsin(br)]dr (1-3-12) 根据欧拉公式,式(1-3-12)可转化为: As(+vsin(r+sinr+vsin(br)]d (1-3-13) 式(1-313)的积分包括实数部分和虚数部分。根据光学相关知识,光波的振幅仅需讨论 实数部分,其展开式为 A(cos(ur)co[wsin(r)]-sin(urd)sin[vsin(hr )])dr (1-3-14) 根据第一类贝塞尔函数的生成函数可有: cosLvsin(br]2Jco(2mbr) (1-3-15) sin[vsin(br)]-2>Jzmtsin[(2m+1)bx] (1-3-16) 将式(1-3-15)和式(1-3-16)代入式(1-3-14)并积分,则有: A-2-ms2+a20} (u6-2mb)a/2 (1-3-17) 2n6222+2222到 [u6-(2m+1)b]a/2 由四血二=1可知,式(13-17)中的每项只有当分母趋于0时才能得到极大值。用 是表示2m及2m+1,则有: u6士kb=0 (1-3-18) 由式(1-3-8)~式(1-3-11)和式(1-3-18)可得: Asin0=±ka k=0,1,2,. (1-3-19) 式(1-3-19)为超声光栅拉曼-奈斯衍射的光强极大条件,该式与光学平面光栅衍射的极大 条件在形式上完全相同。由此可见,当超声波在液体中传播时液体起到了与光学平面光 栅类似的作用,因而有超声波传播的液体被称为超声光栅。根据式(1-319)可知,超声光 栅所对应的光栅常数即为超声波波长A。 当衍射角0。很小时,式(1-3-19)可近似为: A0≈士k入 k=0,1,2. (1-3-20) -15
— 15 — 再令 u= 2π λ (1G3G9) v= 2πΔnL λ (1G3G10) b= 2π Λ (1G3G11) 则式(1G3G7)可简化为: AS =∫ a 2 - a 2 A′exp{j[uxδ+vsin(bx)]}dx (1G3G12) 根据欧拉公式,式(1G3G12)可转化为: AS =∫ a 2 - a 2 {cos[uxδ+vsin(bx)]+jsin[uxδ+vsin(bx)]}dx (1G3G13) 式(1G3G13)的积分包括实数部分和虚数部分.根据光学相关知识,光波的振幅仅需讨论 实数部分,其展开式为: ASR =∫ a 2 - a 2 {cos(uxδ)cos[vsin(bx)]-sin(uxδ)sin[vsin(bx)]}dx (1G3G14) 根据第一类贝塞尔函数J的生成函数可有: cos[vsin(bx)]=2∑ ∞ m=0 J2mcos(2mbx) (1G3G15) sin[vsin(bx)]=2∑ ∞ m=0 J2m+1sin[(2m +1)bx] (1G3G16) 将式(1G3G15)和式(1G3G16)代入式(1G3G14)并积分,则有: ASR =a∑ ¥ m=0 J2m sin[(uδ+2mb)a/2] (uδ+2mb)a/2 + sin[(uδ-2mb)a/2] { (uδ-2mb)a/2 } - a∑ ¥ m=0 J2m+1 sin{[uδ+ (2m +1)b]a/2} [uδ+ (2m +1)b]a/2 + sin{[uδ- (2m +1)b]a/2} { [uδ- (2m +1)b]a/2 } (1G3G17) 由limx→0 sinx x =1可知,式(1G3G17)中的每项只有当分母趋于0时才能得到极大值.用 k 表示2m 及2m+1,则有: uδ±kb=0 (1G3G18) 由式(1G3G8)~式(1G3G11)和式(1G3G18)可得: Λsinθk =±kλ k=0,1,2, (1G3G19) 式(1G3G19)为超声光栅拉曼G奈斯衍射的光强极大条件,该式与光学平面光栅衍射的极大 条件在形式上完全相同.由此可见,当超声波在液体中传播时液体起到了与光学平面光 栅类似的作用,因而有超声波传播的液体被称为超声光栅.根据式(1G3G19)可知,超声光 栅所对应的光栅常数即为超声波波长Λ. 当衍射角θk 很小时,式(1G3G19)可近似为: Λθk ≈±kλ k=0,1,2, (1G3G20)

物理实验教程一近代物理失检O 三、超声光栅测量液体中的声速 超声波在液体中传播的速度可表示为: ,=A (1-3-21) 根据超声光栅拉曼-奈斯衍射的光强极大条件式(1-3-19)可知,只要已知入射光波长 入,测出第k级衍射条纹对应的衍射角。,即可获得超声波波长A:再测出超声波频率f, 就可由式(1-3-21)计算出液体中的声速。因此,利用超声光栅可以测量液体中的声速。 超声光栅测声速是一种高精度测量液体中声速的方法。精确测量液体中的声速对研 究液体的物理和化学性质有重要意义。例如:对有机液体,可以通过测量声速来研究液体 的分子结构:对电解质溶液,可以通过测量声速得到液体密度变化和离子价之间的关系。 【实验器材】 实验器材包括WSG1型超声光栅声速仪和光路系统两部分(图1-3-4),其中光路系 统由光源、分光计(小Y-1型)、液体槽、测微目镜等组成。 接声速仅 12 (a)光路系统 0p99 10//1112 (b)WSG-1形相声光棚声速仪而板 图1-3-4超声光栅测量声速实验装置 1一光源:2一狭缝:3一平行光管:4一液体抽:5-载物台:6一镇紧螺钉 7一望远镜筒:8一测微日镜:9一领率显示0一电源开关11一颜率调节:12一信号输出 实验时,应首先对分光计进行调整。拆下液体槽,用阿贝日镜替换测微日镜,借助平 面反射镜用自准直法调节,使望远镜聚焦于无穷远,望远镜的光轴与分光计的转轴垂直, 平行光管与望远镜同轴并发射平行光,载物台面与分光计的转轴垂直。调节目镜使视野 中分划板刻线清晰,并以平行光管发射的平行光为准,调节望远镜物镜焦距使狭缝像清晰 且细锐明亮。 分光计调整好后,装上液体槽,槽内注入待测液体,扣上盖板,并用导线与超声光棚声 速仪连接。盖板上固定有结钛酸铅陶瓷片(或称PZT品体)。PZT品体在高颜电信号(由 超声光栅声速仪提供)激励下可产生超声波,超声波沿液体槽传播,在液体中形成超声光 栅,当有平行光入射时会发生衍射。打开光源和超声光栅声速仪,适当调节输出超声波频 率,通过望远镜可看到清晰的衍射条纹,此时将阿贝日镜换为测微日镜,就可测量衍射条 纹间距。 光源可使用钠灯或汞灯。钠灯发射的钠黄光波长为589.3nm。汞灯含有3条谱线, 16-
— 16 — 三、超声光栅测量液体中的声速 超声波在液体中传播的速度可表示为: v=Λf (1G3G21) 根据超声光栅拉曼G奈斯衍射的光强极大条件式(1G3G19)可知,只要已知入射光波长 λ,测出第k 级衍射条纹对应的衍射角θk,即可获得超声波波长Λ;再测出超声波频率f, 就可由式(1G3G21)计算出液体中的声速.因此,利用超声光栅可以测量液体中的声速. 超声光栅测声速是一种高精度测量液体中声速的方法.精确测量液体中的声速对研 究液体的物理和化学性质有重要意义.例如:对有机液体,可以通过测量声速来研究液体 的分子结构;对电解质溶液,可以通过测量声速得到液体密度变化和离子价之间的关系. 【实验器材】 实验器材包括 WSGG1型超声光栅声速仪和光路系统两部分(图1G3G4),其中光路系 统由光源、分光计(JJYG1型)、液体槽、测微目镜等组成. 图1G3G4 超声光栅测量声速实验装置 1—光源;2—狭缝;3—平行光管;4—液体槽;5—载物台;6—锁紧螺钉; 7—望远镜筒;8—测微目镜;9—频率显示;10—电源开关;11—频率调节;12—信号输出 实验时,应首先对分光计进行调整.拆下液体槽,用阿贝目镜替换测微目镜,借助平 面反射镜用自准直法调节,使望远镜聚焦于无穷远,望远镜的光轴与分光计的转轴垂直, 平行光管与望远镜同轴并发射平行光,载物台面与分光计的转轴垂直.调节目镜使视野 中分划板刻线清晰,并以平行光管发射的平行光为准,调节望远镜物镜焦距使狭缝像清晰 且细锐明亮. 分光计调整好后,装上液体槽,槽内注入待测液体,扣上盖板,并用导线与超声光栅声 速仪连接.盖板上固定有锆钛酸铅陶瓷片(或称 PZT 晶体).PZT 晶体在高频电信号(由 超声光栅声速仪提供)激励下可产生超声波,超声波沿液体槽传播,在液体中形成超声光 栅,当有平行光入射时会发生衍射.打开光源和超声光栅声速仪,适当调节输出超声波频 率,通过望远镜可看到清晰的衍射条纹,此时将阿贝目镜换为测微目镜,就可测量衍射条 纹间距. 光源可使用钠灯或汞灯.钠灯发射的钠黄光波长为589.3nm.汞灯含有3条谱线

0 光学测量技术实验第1章 分别为:汞蓝光,波长为435.8nm:汞绿光,波长为546.1nm;汞黄光,波长为578.0nm。 设入射光波长为1,士级衍射条纹间距为2d:,则第k级衍射条纹对应的衍射角 日。 (1-3-22) 式中,F为望远镜物镜焦距。对JJY-1型分光计,F=170mm。从超声光栅声速仪上读出 当前超声波频率f,则根据式(1-3-20)和式(1-3-21)可得透明液体中的声速为: k=0,1,2,. (1-3-23 如果实验中观察到的衍射条纹不理想,可轻微改变液体槽盖板的角度,以保证声源面 与液体槽端面严格平行。应随时检查液面高度,当液面较低时,要及时补充液体至正常液 面线处,防止因液体过度挥发导致液面低于PZT品体而影响观测效果。 【实验内容】 1,基础性实验内容 (1)测量几种透明液体中的声速。 测量要求为:①提供的液体包括蒸馏水,乙醇、甘油等,每种液体至少要测量三级衍 射条纹:②更换液体时,一定要将液体槽擦拭干净,以免影响测量准确度:③根据表1-3-1 中提供的数据,由式(1-324)计算当前温度t下不同液体中的声速,然后与测量值比 较,求取相对不确定度,并分析误差产生的原因。 =。+g(t一) (1-3-24) 式中,。是温度为1。时液体中的声速:a是温度系数。 表131几种不同透明液体中的声速 体名称 温度1o/ 声速/(m·g) 温度系数a/(m·1·K-) 装胺 20 1656 -4.6 丙附 20 1192 -5.5 20 1326 -5.2 煮馏水 25 1497 2.5 甘油 20 1923 -1.8 煤油 34 1295 甲酵 20 1123 -3.3 乙醇 20 1180 -3.6 (2)测量声速与液体浓度的关系。 配置几种不同浓度的蔗糖溶液,分别测量其中的声速,并分析声速与溶液浓度的关 系。配置溶液时应保证溶液的洁净度,若存在悬浮颗粒则会对测量效果影响很大。 2.设计性实验内客 根据现有实验条件,设计实验方案测量柴油的密度 实验要求为:阐述实验基本原理和方法,说明测量系统组成和基本实验步骤,进行实 -17
— 17 — 分别为:汞蓝光,波长为435.8nm;汞绿光,波长为546.1nm;汞黄光,波长为578.0nm. 设入射光波长为λ,±k 级衍射条纹间距为2dk,则第k 级衍射条纹对应的衍射角 θk 为: θk = dk F (1G3G22) 式中,F 为望远镜物镜焦距.对JJYG1型分光计,F=170mm.从超声光栅声速仪上读出 当前超声波频率f,则根据式(1G3G20)和式(1G3G21)可得透明液体中的声速为: v=kλF f dk k=0,1,2, (1G3G23) 如果实验中观察到的衍射条纹不理想,可轻微改变液体槽盖板的角度,以保证声源面 与液体槽端面严格平行.应随时检查液面高度,当液面较低时,要及时补充液体至正常液 面线处,防止因液体过度挥发导致液面低于 PZT 晶体而影响观测效果. 【实验内容】 1.基础性实验内容 (1)测量几种透明液体中的声速. 测量要求为:① 提供的液体包括蒸馏水、乙醇、甘油等,每种液体至少要测量三级衍 射条纹;② 更换液体时,一定要将液体槽擦拭干净,以免影响测量准确度;③ 根据表1G3G1 中提供的数据,由式(1G3G24)计算当前温度t 下不同液体中的声速vt,然后与测量值比 较,求取相对不确定度,并分析误差产生的原因. vt =v0 +α(t-t0) (1G3G24) 式中,v0 是温度为t0 时液体中的声速;α 是温度系数. 表1G3G1 几种不同透明液体中的声速 液体名称 温度t0/℃ 声速v0/(ms-1) 温度系数α/(ms-1K-1) 苯 胺 20 1656 -4.6 丙 酮 20 1192 -5.5 苯 20 1326 -5.2 蒸馏水 25 1497 2.5 甘 油 20 1923 -1.8 煤 油 34 1295 — 甲 醇 20 1123 -3.3 乙 醇 20 1180 -3.6 (2)测量声速与液体浓度的关系. 配置几种不同浓度的蔗糖溶液,分别测量其中的声速,并分析声速与溶液浓度的关 系.配置溶液时应保证溶液的洁净度,若存在悬浮颗粒则会对测量效果影响很大. 2.设计性实验内容 根据现有实验条件,设计实验方案测量柴油的密度. 实验要求为:阐述实验基本原理和方法,说明测量系统组成和基本实验步骤,进行实

物理实验教程一近代物理失检O 际实验测量,选择合理方法处理实验数据,分析与讨论实验结果。 【注意事项】 (1)拆装液体槽、补充或更换液体时,应关闭超声光栅声速仪,同时不要接触液体槽 通光面,以免污染而影响测量。 (2)实哈中要群免振动,因为振动会破坏超声光棚,浩成测量失败 (3)实验时间不宜过长,因为时间过长不仅会因液体温度升高降低测量准确度,而且 会使振荡线路过热,损坏仪器。 (④)实验结柬后必须将液体倒出,并将PZT晶体表面和液体槽擦干。 (5)本装置的PZT晶体直接插入液体中,因此不能测量电解质溶液。 【思考与讨论】 (1)实验时可以发现,调节频率可使衍射条纹很清楚,但过一会就模糊或消失,试分 析其原因。 (2)由驻波理论可知,相邻波腹间的距离和相邻波节间的距离都等于半波长,那么为 什么超声光栅的光栅常数等于超声波波长? (3)光学平面光栅和超声光栅有何异同? (4)实验中能否用逐差法处理数据?如果能,从测量角度看应该怎样做? 【参考文献】 [1]袁易全.近代超声学原理及应用.南京:南京大学出版杜,1996。 [2]杜功焕,来哲民,龚秀芬.声学基础.南京:南京大学出版社,2012. [3] 姚启钧.光学教程.北京:高等教育出版社,2008. [4]俞宽新,丁晓红,庞光广,声光原理与声光器件,北京:科学出版社,2011, [5]刘雪凌,唐志列,阮立锋.超声光的光栅常数理论研究.大学物理,2013,32(5) 24-26. [6]王锁明,侯彬,朱二旷,等.基于超声光栅衍射的液体密度测试.物理实验,2013 33(4):41-43. [?]丁冠阳,唐军杰,王爱军,超声光栅测声速实验方法的探索,大学物理实验,2014, 27(6):64-66. 实验1-4脉冲固体激光器基本特性参数测量 激光(laser,light amplification by stimulated emission of radiation)是20世纪60年 代的伟大发明。激光的诞生开启了近代光学的大门,使整个光学领域的面貌焕然一新。 激光作为一种新型光源,具有方向性强、单色性好以及亮度高等突出特点。这些特点使激 光的应用特别广泛,从物理、化学到天文、地理,从生物、医学到无线电、计算机,从农业到 18
— 18 — 际实验测量,选择合理方法处理实验数据,分析与讨论实验结果. 【注意事项】 (1)拆装液体槽、补充或更换液体时,应关闭超声光栅声速仪,同时不要接触液体槽 通光面,以免污染而影响测量. (2)实验中要避免振动,因为振动会破坏超声光栅,造成测量失败. (3)实验时间不宜过长,因为时间过长不仅会因液体温度升高降低测量准确度,而且 会使振荡线路过热,损坏仪器. (4)实验结束后必须将液体倒出,并将 PZT 晶体表面和液体槽擦干. (5)本装置的 PZT 晶体直接插入液体中,因此不能测量电解质溶液. 【思考与讨论】 (1)实验时可以发现,调节频率可使衍射条纹很清楚,但过一会就模糊或消失,试分 析其原因. (2)由驻波理论可知,相邻波腹间的距离和相邻波节间的距离都等于半波长,那么为 什么超声光栅的光栅常数等于超声波波长? (3)光学平面光栅和超声光栅有何异同? (4)实验中能否用逐差法处理数据? 如果能,从测量角度看应该怎样做? 【参考文献】 [1] 袁易全.近代超声学原理及应用.南京:南京大学出版社,1996. [2] 杜功焕,朱哲民,龚秀芬.声学基础.南京:南京大学出版社,2012. [3] 姚启钧.光学教程.北京:高等教育出版社,2008. [4] 俞宽新,丁晓红,庞兆广.声光原理与声光器件.北京:科学出版社,2011. [5] 刘雪凌,唐志列,阮立锋.超声光栅的光栅常数理论研究.大学物理,2013,32(5): 24G26. [6] 王锁明,侯彬,朱二旷,等.基于超声光栅衍射的液体密度测试.物理实验,2013, 33(4):41G43. [7] 丁冠阳,唐军杰,王爱军.超声光栅测声速实验方法的探索.大学物理实验,2014, 27(6):64G66. 实验1G4 脉冲固体激光器基本特性参数测量 激光(laser,lightamplificationbystimulatedemissionofradiation)是20世纪60年 代的伟大发明.激光的诞生开启了近代光学的大门,使整个光学领域的面貌焕然一新. 激光作为一种新型光源,具有方向性强、单色性好以及亮度高等突出特点.这些特点使激 光的应用特别广泛,从物理、化学到天文、地理,从生物、医学到无线电、计算机,从农业到