
卡持动力学方程的讨论 方程可重写为: 2MRDCot= -[1+(z-1)y]2/3 apro 2 z-1 -(1-y)2/3 固体颗粒完全反应时,=1,令所需时间为T,则: 2MRDCo 2-z2/3 apro 2 = z-1 a)对平板状颗粒, 29:=-r 2029= b)对圆柱形颗粒, 2 MRDCo:=名=(1-21-pn+1-201-p】 zln(z) apro 2 2(2-1) 2MRDCeTY apro 2 2(z-1) ???
卡特动力学方程的讨论 方程可重写为: 固体颗粒完全反应时, y=1, 令所需时间为 Tf,则: a) 对平板状颗粒, b) 对圆柱形颗粒, ???

1.52商 1.50 148 748e 0.6 柔 1.46 0.7 3+ 1.44 0.8 1.42 1.40 0.9 138 母 1.34 Carter 1.32 1.0 1 20 25 Time,hours mooringue →NiO ae 0.35 o.6 74%8gs 0.7 0.s0 0.8 0.55 Ginstling C.75 0.70 20 25 Fig.7-32.Plotting the kinetics of the reaction Ni+Oz-NiO,ac- cording to Crank-Ginstling and Brounshtein [Carter (1963)]
Carter Ginstling

Summary.A summary of the equations applicable to reactions controlled by diffusion through a nonporous solid product layer is given in Table 7-7. To facilitate evaluation of kinetic data for any value of the fraction reacted, R,the plots of the functions. y-1-(I-R)13 y=[1-(1-R)3]2 y=1-子R-(1-R)23 5-0 are given in Fig.7-35. 03 3 0102304a500780910 Frottion reacted,R Fig.7-35.Plots of different kineties equations

Table 7-7.Kinetic equations applicable to reactions controlled by diffusion through non- porous solid product.Reacting solid has the geometry of a sphere. 1)Jander's equation [l -(1-R)=kr Approximate 2)Crank-Ginstling Applicable to most and Brounshtcin's 1一子R一1-)23=k1 cases although not equation very exact 3)Valensi's equation [1 +(z-1)R]2.3+(z-1)(1-R)2/3 =kt Exact equation. LITERATURE Historical W.J.Mellor,Chemical Starics and Dynamics,London,Longmans,1904. C.F.Wenzel,Lehre ron Verwandrschaf,Dresden,1777.(First studies on rates of chemical reactions;rate of dissolution of metals in acids and the effect of acid concentration.) Introduction S.Glasstone,Textbook of Physical Chemistry,Princeton,Van Nostrand,1946. S.Glasstone and D.Lewis.Elements of Physical Chemistry (2nd ed.).Princeton,Van No- strand,1960. J.C.Jungers,et al.,Cinetique Chimique Appitqude,Paris,Technip,1958. K.J.Laidler,Chemical Kinerics (2nded.),New York,McGraw-Hill,1965. E.A.Moelwyn-Hughs,The Kinetics of Reactions in Solution,Oxford,Clarendon,1947. G.Pannetier and P.Souchay,Chemfcal Kinetics(trans.from French).New York,Elsevier, 1967

Kinetics of solid state reactions Phenomenological description of growth rate:W=kt W n Rate-determining process W=kt 1 chemical (interface)reaction W=k-ti2 112 diffusion through relative thin reactant/product layer W=k-til3 1/13 nucleation n=1:A porous or non-closed product layer is formed when e.g.: Gases are evolved during the reaction Volume differences exist between reactants and products n=1/2:Dense,closed layer is formed:diffusion is rate limiting step Parabolic rate law
Kinetics of solid state reactions Phenomenolo gical description of growth rate: W kt n g g W n Rate-determining process W = k1t 1 chemical (interface) reaction W = k2t1/2 1/2 diffusion through relative thin reactant/product layer W = k3t1/3 1/3 nucleation n = 1: A porous or non-closed product layer is formed when e.g.: – Gases are evolved during the reaction – Volume differences exist between reactants and products Volume differences exist between reactants and products n = 1/2: Dense, closed layer is formed: diffusion is rate limiting step – Parabolic rate law
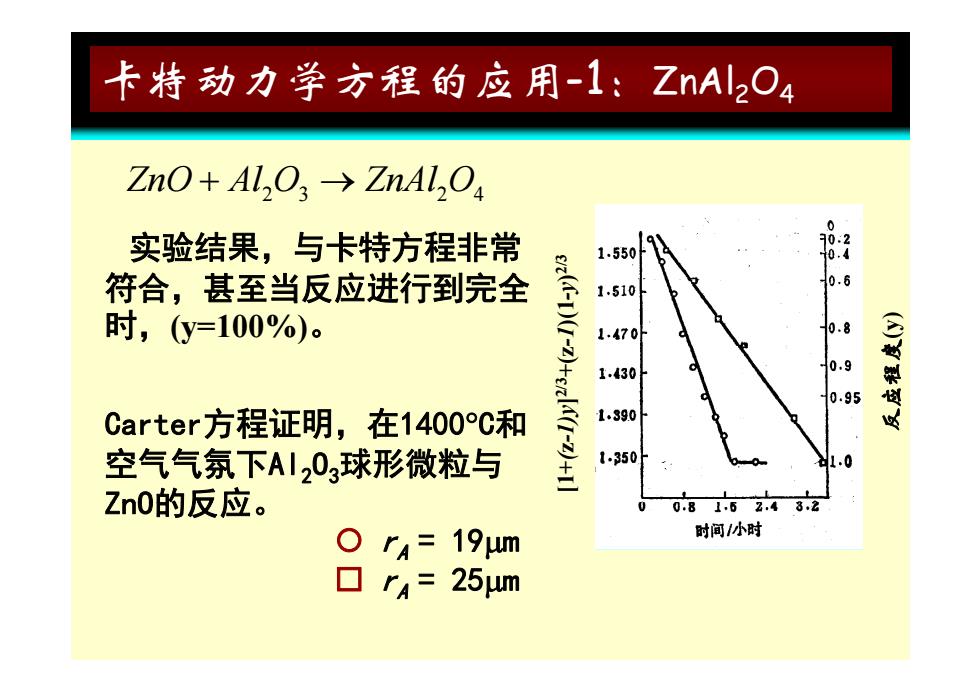
卡特动力学方程的应用-1:ZnAl2O4 ZnO+AL,O3→ZnAl,O, 实验结果,与卡特方程非常 1550 8 符合,甚至当反应进行到完全 1.510 时,(y=100%)。 1 1.430 0.9 0.95 Carter方程证明,在1400C和 1.390 空气气氛下AI03球形微粒与 +三 1350 0 Zn0的反应。 0815z.48,2 r=19um 时间小时 口r4= 25μm
卡特动力学方程的应用-1 :ZnAl 2 O 4 ZnO Al O ZnAl O 23 24 实验结果,与卡特方程非常 2/3 符合,甚至当反应进行到完全 时,(y=100%) 。 -1)(1-y)2 度(y) Carter方程证明 在1400 C 和 1)y]2/3+(z- 反应程度 Carter方程证明,在1400 C 和 空气气氛下Al 2 O 3球形微粒与 ZnO的反应 [1+(z-1) 反 ZnO的反应 。 rA = 19 m rA = 25 m

卡特动力学方程的应用-1:ZnAl2O4 必须指出,该反应是在1400°℃下,充满Zn0的坩 埚中悬浮一些大小相同的a-A10微粒进行的, 实际上A1,03微粒被活度为1的Zn0蒸气包围着, 反应实际上是一个气-固相反应。 下面实验可以证实该假设:将AI,0,单晶悬浮在 由Zn0制成的坩埚中,使得反应仅仅是在Zn0的 蒸气中进行,结果发现,其反应速率常数与固 固反应的速率常数完全一致
卡特动力学方程的应用-1:ZnAl 2 O 4 必须指出,该反应是在1400 C下,充满ZnO的坩 埚中悬浮 些大小相同的 一些大小相同的 -Al 2 O 3微粒进行的, 实际上Al 2 O 3微粒被活度为1的ZnO蒸气包围着, 反应实际上是一个气 -固相反应 。 下面实验可以证实该假设:将 下面实验可以证实该假设:将Al 2 O 3单晶悬浮在 由ZnO制成的坩埚中,使得反应仅仅是在ZnO的 蒸气中进行 结果发现 其反应速率常数与固 蒸气中进行,结果发现,其反应速率常数与固 -固反应的速率常数完全一致

卡特动力学方程的应用-2:NiO 在空气中Ni球氧化过程 采用Carter方程, 1.52 0. 反应进行到100% 1.50 1.48 时仍能很好地与 1.46 0.7 1.44 74μm球 0.8 计算值符合,如果 .1040℃ 1.42 0.9 采用Jander方程, 1.40 149μm球 1130℃ 1.38 y>0.5就会有较大 1.36 误差。 1.34 1.32 .0 10 15 20 时间(h)
卡特动力学方程的应用-2:NiO 在空气中Ni球氧化过程 采用Carter方程, 反应进行到100% 时仍能很好地与 1)(1-y)2/3 (y) 计算值符合,如果 采用Jander方程, y]2/3+(z-1 反应程度( y>0.5就会有较大 误差。 [1+(z-1)y 反 [

上述动力学方程的应用条件 不论是Janderi还Carter方程,均假定在高温下,反应 物的颗粒表面上的扩散速度是非常快的,或者反应物之一 在反应温度下有足够高的蒸气压,可以快速地通过气相进 行输运,使得反应物之一的活度能够保持恒定。如果该条 件不能被满足,则反应的动力学不仅要受r/r比值的影响, 而且还要受到r和r的绝对值的影响。 当r超过一定值时,A颗粒本身就要相互接触,不再可 能被B包围着,反应将不再按照上述动力学方程进行。 在较低的温度下进行粉末反应时,反应物的粒度大小、 粒度分布、装紧程度以及接触面积等也将会对反应的动力 学过程产生重要影响,在推导动力学方程时必须加以考虑
上述动力学方程的应用条件 不论是Jander 还Carter方程 均假定在高温下 反应 方程,均假定在高温下,反应 物的颗粒表面上的扩散速度是非常快的,或者反应物之一 在反应温度下有足够高的蒸气压 可以快速地通过气相进 在反应温度下有足够高的蒸气压,可以快速地通过气相进 行输运,使得反应物之一的活度能够保持恒定。如果该条 件不能被满足 则反应的动力学不仅要受 件不能被满足,则反应的动力学不仅要受 rA/ rB比值的影响, 而且还要受到 rA和 rB的绝对值的影响。 当 rA超过 定值时, 一 A颗粒本身就要相互接触,不再可 颗粒本身就要相互接触,不再可 能被B包围着,反应将不再按照上述动力学方程进行。 在较低的温度下进行粉末反应时,反应物的粒度大小、 粒度分布、装紧程度以及接触面积等也将会对反应的动力 学过程产生重要影响,在推导动力学方程时必须加以考虑

固相反应动力学方程小结 扩散过程控制 平板、抛物线 +2 2DCM 规律: t=kt 球形粉末、 Jander方程: (1-1-y)2=2kt/R2 x=r[1-(1-) app 球形粉末、 3y-1-29=3 C二Mp Ginstling方程: Z= aVR 球形粉末、 Valensi or [1+(2-1)x3+(2-101-x)23=z+(1-z) 2DCo Carter方程: ER2
固相反应动力学方程小结扩散过程控制 2DC M x t kt ρ DC M x 2 0 2 Rr 平板、抛物线 规律: 球形粉末、 J d 方程 2 2 3 ( 1 1 y ) 2kt/R 1/3 xr y 1 1 αρ Jan der方程: 3 ( 1 1 y ) 2kt/R 2/3 0 2 2 2 1 (1 ) 3 D C yy t R P p M αρ ε V 球形粉末、 Ginstling方程: 2/3 2/3 2DC R p α V V z 球形粉末、 Vl i 2/3 2/3 0 2 2 1 ( 1) ( 1)(1 ) (1 ) DC zx z x z z t R Valensi or Carter方程: