
3.电子导电:半导体 纯度 对纯度要求极高(半导体纯硅:99.999999999%); 掺杂浓度需要精确可控; ● 结构 单晶、多晶、无定形; 成分 元素半导体、二元半导体、三元半导体; 分类(通常按载流子的来源) >本征半导体:载流子主要来自其本身 >非本征(杂质)半导体:载流子主要来自外部掺杂
3.电子导电:半导体 1 • 纯度 对纯度要求极高(半导体纯硅:99.999999999%); 掺杂浓度需要精确可控; • 结构 单晶、多晶、无定形; • 成分 元素半导体、二元半导体、三元半导体; ➢ 本征半导体:载流子主要来自其本身 ➢ 非本征(杂质) 半导体:载流子主要来自外部掺杂 • 分类(通常按载流子的来源):
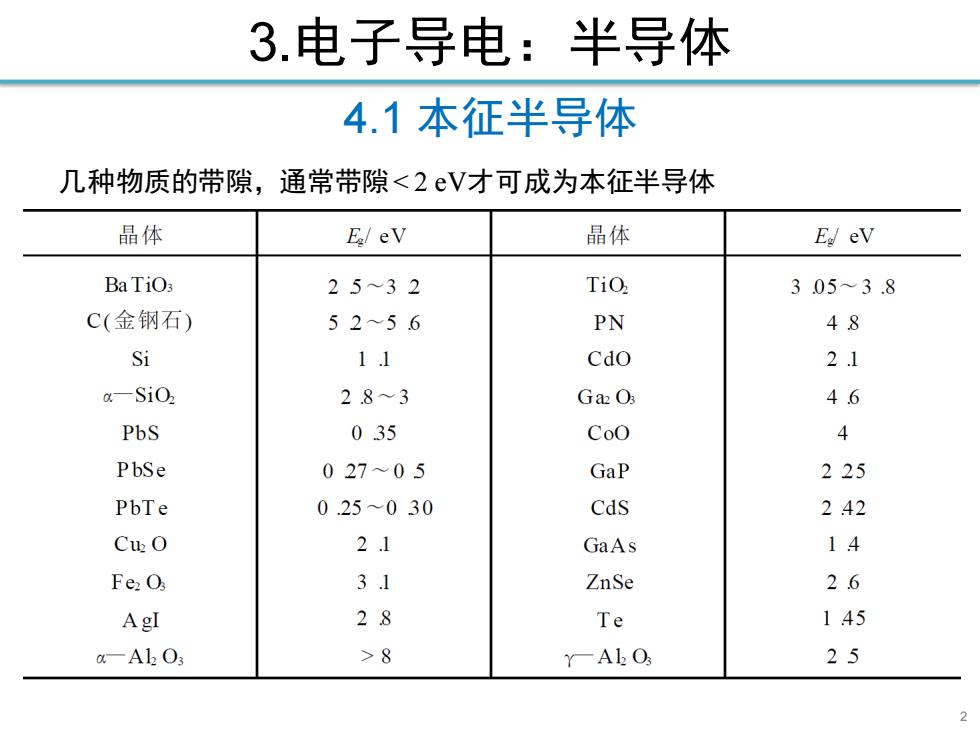
3.电子导电:半导体 4.1本征半导体 几种物质的带隙,通常带隙8 YAk Os 25
3.电子导电:半导体 2 4.1 本征半导体 几种物质的带隙,通常带隙< 2 eV才可成为本征半导体
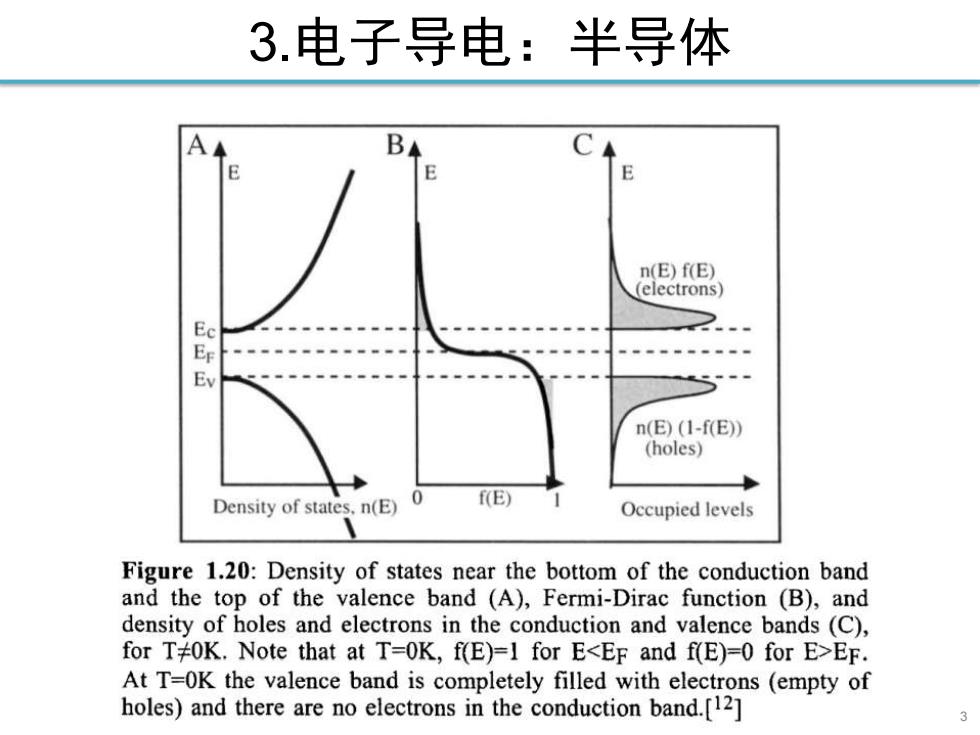
3.电子导电:半导体 A B n(E)f(E) (electrons) Ec 2 Ev n(E)(1-fE) (holes) Density of states,n(E)0 f(E) 4 Occupied levels Figure 1.20:Density of states near the bottom of the conduction band and the top of the valence band (A),Fermi-Dirac function (B),and density of holes and electrons in the conduction and valence bands(C), for T#OK.Note that at T=0K,f(E)=1 for EEF. At T=OK the valence band is completely filled with electrons (empty of holes)and there are no electrons in the conduction band.[12]
3.电子导电:半导体 3

3.电子导电:半导体 载流子仍然只有电子,但是用“电子”和“空穴”两个概念描述导 带和价带中的导电行为。并且沿用了“半经典近似” 导带 导带 电子 价带 价带 T=0K:满带,不导电 T>0K:导带和价带都成 为了未满带,导电
3.电子导电:半导体 4 载流子仍然只有电子,但是用“电子”和“空穴”两个概念描述导 带和价带中的导电行为。并且沿用了“半经典近似” T = 0 K:满带,不导电 T > 0 K:导带和价带都成 为了未满带,导电

3.电子导电:半导体 电子: >特指脱离价带、进入导带以后的 准自由电子 >带负电 >在导带底m。*>0 空穴: B >价电子脱离价带后在价带中形成 的空位,是一种假想粒子 >带正电 >在价带顶m,*>0(与同一状态电子 符号相反,大小相等) >与对应的空缺k态电子运动规律 相同,产生电流相反 (e
3.电子导电:半导体 5 电子: ➢ 特指脱离价带、进入导带以后的 准自由电子 ➢ 带负电 ➢ 在导带底me *>0 空穴: ➢ 价电子脱离价带后在价带中形成 的空位,是一种假想粒子 ➢ 带正电 ➢ 在价带顶mh *>0 (与同一状态电子 符号相反,大小相等) ➢ 与对应的空缺k态电子运动规律 相同,产生电流相反

3.电子导电:半导体 一)导带中的电子浓度 ·半导体中电子能量(E)或空穴能量(E)表达式与金属中自 由电子能量表达式,形式上基本相同, 质量用有效质量代替: 电子:E。=E。+2 e* 空穴:Eh=E,- h2k2 2mn 能Eg E。:导带底能量 m。*:电子有效质量 Z八E) Ev:价带顶能量 n*: 空穴有效质量 自由电子近似导出的状态密度对于半导体同样有效
3.电子导电:半导体 • 半导体中电子能量(Ee)或空穴能量(Eh)表达式与金属中自 由电子能量表达式,形式上基本相同,质量用有效质量代替: 6 • 自由电子近似导出的状态密度对于半导体同样有效。 一)导带中的电子浓度 电子:𝐸𝑒 = 𝐸𝑐 + ħ 2𝑘 2 2𝑚𝑒 ∗ 空穴:𝐸ℎ = 𝐸𝑣 − ħ 2𝑘 2 2𝑚ℎ ∗ Ec:导带底能量 Ev:价带顶能量 me *:电子有效质量 mh * :空穴有效质量 Ev Ec Eg
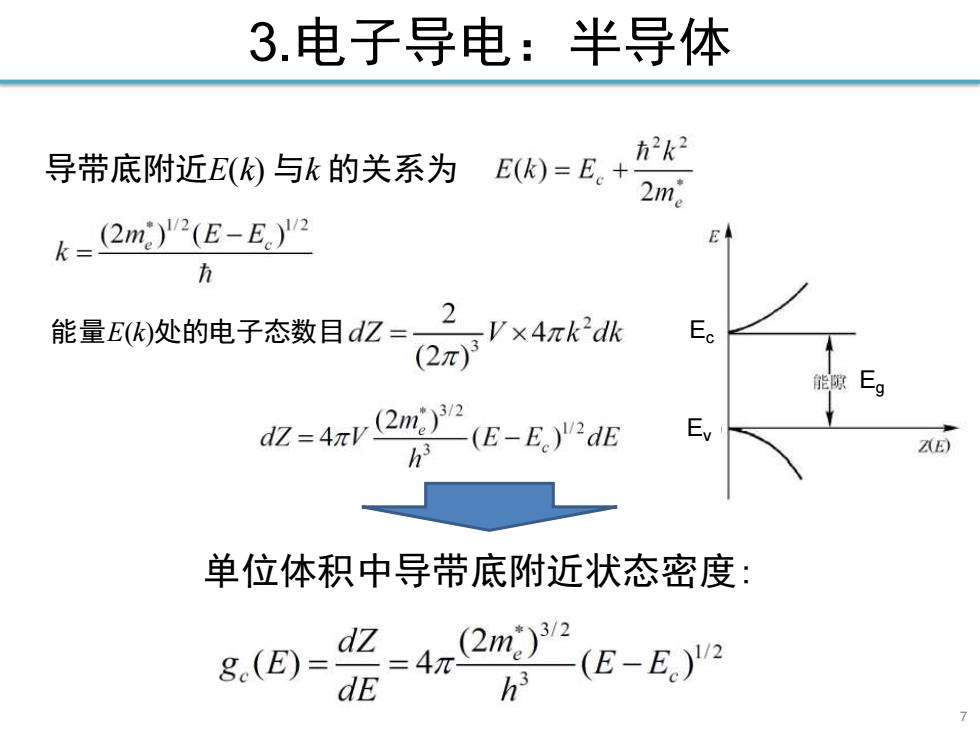
3.电子导电:半导体 导带底附近E((与k的关系为E(k)=E。+ 方2k2 2m k=2m)'2(E-E2 h 2 能量E(处的电子态数目dZ= V×4πk2dk (2π) 能隙 =(E-EdE h 2ZE) 单位体积中导带底附近状态密度: 8.(E)=2=4z2m —(E-E)2 dE
3.电子导电:半导体 7 导带底附近E(k) 与k 的关系为 单位体积中导带底附近状态密度: Ev Ec Eg 能量E(k)处的电子态数目

3.电子导电:半导体 当获得了导带底的状态密度后,根据Fermi分布函数,可以得到 导带的电子浓度为: n=∫f(E)g.(E)dE Ec 5 Conduction Band 室温下,对大部分材料而言E和Ec、E的距离都远远 大于kgT(仅0.026eV,半导体带隙一般为0.5-2eV) Ec 因此,对于导带中的电子,E-Ep>kT,于是Fermi 分布函数可近似为: Ev Many HOLES! Valence Band f(E)=e-6n+ ≈e(E-Er/kBT
3.电子导电:半导体 8 当获得了导带底的状态密度后,根据Fermi 分布函数,可以得到 导带的电子浓度为: 因此,对于导带中的电子,E-EF >> kBT,于是Fermi 分布函数可近似为: 室温下,对大部分材料而言EF和EC、EV的距离都远远 大于kBT(仅0.026eV,半导体带隙一般为0.5−2 eV)

3.电子导电:半导体 fE)=2亚7+=e 1 2jE-,eswaE 利用: -2aVa -ew 3/2 得到导带电子浓度: 同理,可得价带空穴浓度: 3/2 p-0-g,dc-2g) e-(Er-ErYkgT
3.电子导电:半导体 9 利用: 得到导带电子浓度: 同理,可得价带空穴浓度:

3.电子导电:半导体 3/2 e-(Ec-Er)knT 载流子浓度与体系的 Fermi能级密切相关; 成立条件: 3/2 e-(Er-EvVknT Ec-EF>>KBT EE-Ev>>kBT 这种情况下,不管Fermi能级的具体位置如何,在给定温度下,电子和空 穴浓度的乘积总是恒定的,即: np=4 2冰gT 其中E为禁带宽度。注意上式不仅适用于本征半导体,即使存在杂质, 它也是成立的
3.电子导电:半导体 10 • 载流子浓度与体系的 Fermi 能级密切相关; • 成立条件: EC – EF >> kBT EF – EV >> kBT • 这种情况下,不管Fermi 能级的具体位置如何,在给定温度下,电子和空 穴浓度的乘积总是恒定的,即: • 其中Eg为禁带宽度。注意上式不仅适用于本征半导体, 即使存在杂质, 它也是成立的