《电工学》课程PPT教学课件（电工技术）第三章电路的暂态分析

团购合买资源类别：文库，文档格式：PPT，文档页数：72，文件大小：1.83MB

电工学电工技术)第七版多媒体教学课件第3章电路的暂态分析中国矿业大学研制高等教育出版社出版高等教育电子音像出版社

第3章电路的暂态分析 3.1电阻元件、电感元件与电容元件 32储能元件和换路定则 33RC电路的响应 3.4一阶线性电路暂态分析的三要素法 3.5微分电路与积分电路 3.6RL电路的响应。中间对整大琴 2/72 章目录上一页下一页返回退出

2/72 章目录上一页下一页返回退出 3.2 储能元件和换路定则 3.3 RC电路的响应 3.4 一阶线性电路暂态分析的三要素法 3.6 RL电路的响应 3.5 微分电路与积分电路 3.1 电阻元件、电感元件与电容元件第3章电路的暂态分析

第3章电路的暂态分析稳定状态：在指定条件下电路中电压、电流已达到稳定值。暂态过程：电路从一种稳态变化到另一种稳态的过渡过程。研究暂态过程的实际意义 1.利用电路暂态过程产生特定波形的电信号如锯齿波、三角波、尖脉冲等，应用于电子电路。 2.控制、预防可能产生的危害暂态过程开始的瞬间可能产生过电压、过电流使电气设备或元件损坏。。中间对装大$ 372 章目录上一页下一页返回退出

3/72 章目录上一页下一页返回退出稳定状态：在指定条件下电路中电压、电流已达到稳定值。暂态过程：电路从一种稳态变化到另一种稳态的过渡过程。第3章电路的暂态分析 1. 利用电路暂态过程产生特定波形的电信号如锯齿波、三角波、尖脉冲等，应用于电子电路。研究暂态过程的实际意义 2. 控制、预防可能产生的危害暂态过程开始的瞬间可能产生过电压、过电流使电气设备或元件损坏

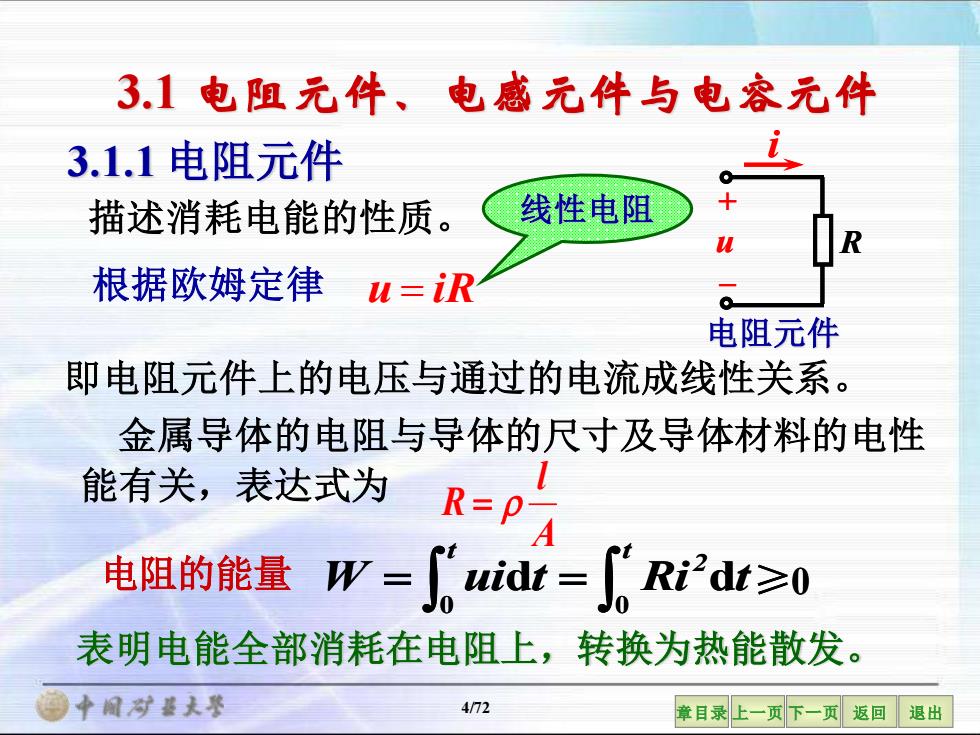
3.1电阻元件、电感元件与电容元件 3.1.1电阻元件描述消耗电能的性质。线性电阻根据欧姆定律u=iR 电阻元件即电阻元件上的电压与通过的电流成线性关系。金属导体的电阻与导体的尺寸及导体材料的电性能有关，表达式为 R=P A 电阻的能量W=idt=iRi2dt≥0 表明电能全部消耗在电阻上，转换为热能散发。酒中间对整大琴 4/72 章目录上一页下一页返回退出

4/72 章目录上一页下一页返回退出 3.1.1 电阻元件描述消耗电能的性质。根据欧姆定律 u = iR 即电阻元件上的电压与通过的电流成线性关系。线性电阻 A l R =  金属导体的电阻与导体的尺寸及导体材料的电性能有关，表达式为表明电能全部消耗在电阻上，转换为热能散发。 3.1 电阻元件、电感元件与电容元件电阻元件 R i u + _ W ui t Ri t t 2 t d d 0 0 电阻的能量 W = ui t = Ri t≥0 t 2 t d d 0 0 = =

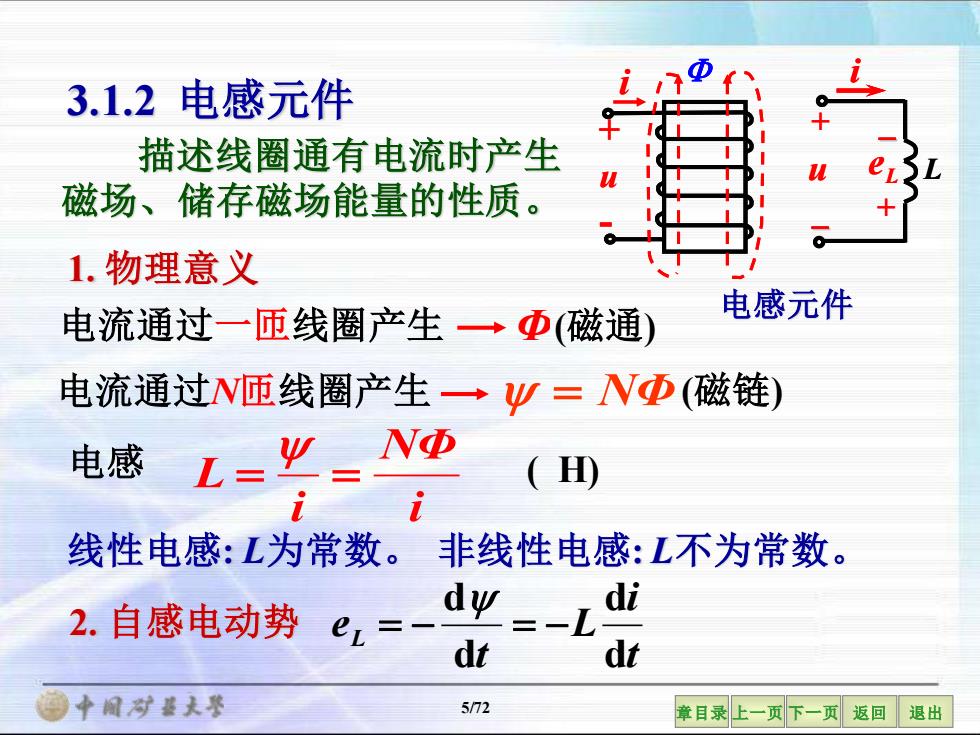
3.1.2电感元件描述线圈通有电流时产生磁场、储存磁场能量的性质。 1.物理意义电流通过一匝线圈产生→Φ（磁通）电感元件电流通过N匝线圈产生一→W=NΦ（磁链）电感 L==N地 i (H) 线性电感：L为常数。非线性电感：L不为常数。 2.自感电动势 e= d=-L i dt t 。中间对装夫举 5/72 章目录上一页下一页返回退出

5/72 章目录上一页下一页返回退出描述线圈通有电流时产生磁场、储存磁场能量的性质。 1. 物理意义 3.1.2 电感元件电感元件 u i  + - i u + L − L e − + i u + L − L e − + i NΦ i L = = 电感  ( H) 线性电感: L为常数。非线性电感: L不为常数。电流通过N匝线圈产生  = NΦ (磁链) 电流通过一匝线圈产生 Φ (磁通) 2. 自感电动势 t i L t eL d d d d = − = − 

3.电感元件储能根据基尔霍夫定律可得 u=-e=L di dt 将上式两边同乘上i,并积分，则得 idr-可idi-L 磁场能 W-ILP 2 即电感将电能转换为磁场能储存在线圈中，当电流增大时，磁场能增大，电感元件从电源取用电能；当电流减小时，磁场能减小，电感元件向电源放还能量。 ©中间对装天举 672 章目录上一页下一页返回退出

6/72 章目录上一页下一页返回退出 3. 电感元件储能 2 2 1 W = Li t i u eL L d d 根据基尔霍夫定律可得 = − = 将上式两边同乘上 i ，并积分，则得 2 0 0 2 1 ui dt Li di Li t i = =   即电感将电能转换为磁场能储存在线圈中，当电流增大时, 磁场能增大, 电感元件从电源取用电能；当电流减小时，磁场能减小，电感元件向电源放还能量。磁场能

3.1.3电容元件描述电容两端加电源后，其两个极板上分别聚集起等量异号的电荷，在介质中建立起电场，并储存电场能量的性质。电容 C= F) 电容元件 W 当电容电压变化时，在电路中产生电流 i=c du dt 将上式两边同乘上W,并积分，则得： id-cudn-Cu 雪中间对基天华 772 章目录上一页下一页返回退出

7/72 章目录上一页下一页返回退出 3.1.3 电容元件描述电容两端加电源后，其两个极板上分别聚集起等量异号的电荷，在介质中建立起电场, 并储存电场能量的性质。电容 u q C = (F ) t u i C d d = 当电容电压u变化时，在电路中产生电流将上式两边同乘上 u，并积分，则得： 2 0 0 2 1 ui dt Cudu Cu t u = =   u i C + _ 电容元件 u i C + _ 电容元件

电容元件储能电场能 w=Icu 即电容将电能转换为电场能储存在电容中，当电压增大时，电场能增大，电容元件从电源取用电能；当电压减小时，电场能减小，电容元件向电源放还能量。本节所讲的均为线性元件，即R、L、C都是常数。 ©中间对装天举 8/72 章目录上一页下一页返回退出

8/72 章目录上一页下一页返回退出即电容将电能转换为电场能储存在电容中，当电压增大时, 电场能增大, 电容元件从电源取用电能；当电压减小时，电场能减小，电容元件向电源放还能量。 2 2 1 W = Cu 电场能电容元件储能本节所讲的均为线性元件，即R、L、C都是常数

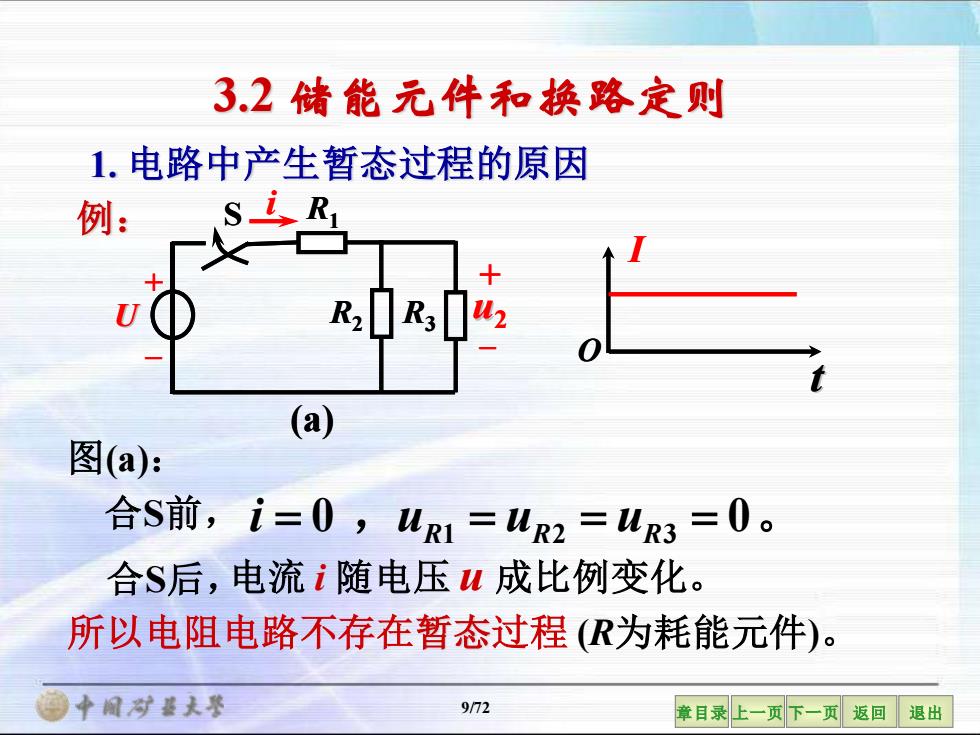
3.2储能元件和换路定则 1.电路中产生暂态过程的原因例： (a) 图(a): 合S前，i=0,lR1=4R2=4R3=0。合S后，电流i随电压u成比例变化。所以电阻电路不存在暂态过程(R为耗能元件)。湾中帽对装天$ 972 章目录上一页下一页返回退出

9/72 章目录上一页下一页返回退出 3.2 储能元件和换路定则 1. 电路中产生暂态过程的原因合S后，电流 i 随电压 u 成比例变化。所以电阻电路不存在暂态过程 (R为耗能元件)。图(a)：合S前， i = 0 ，uR1 = uR2 = uR3 = 0。例： t I O (a) S + _ U R2 R3 u2 + _ R1 i (a) S + _ U R2 R3 u2 + _ R1 i

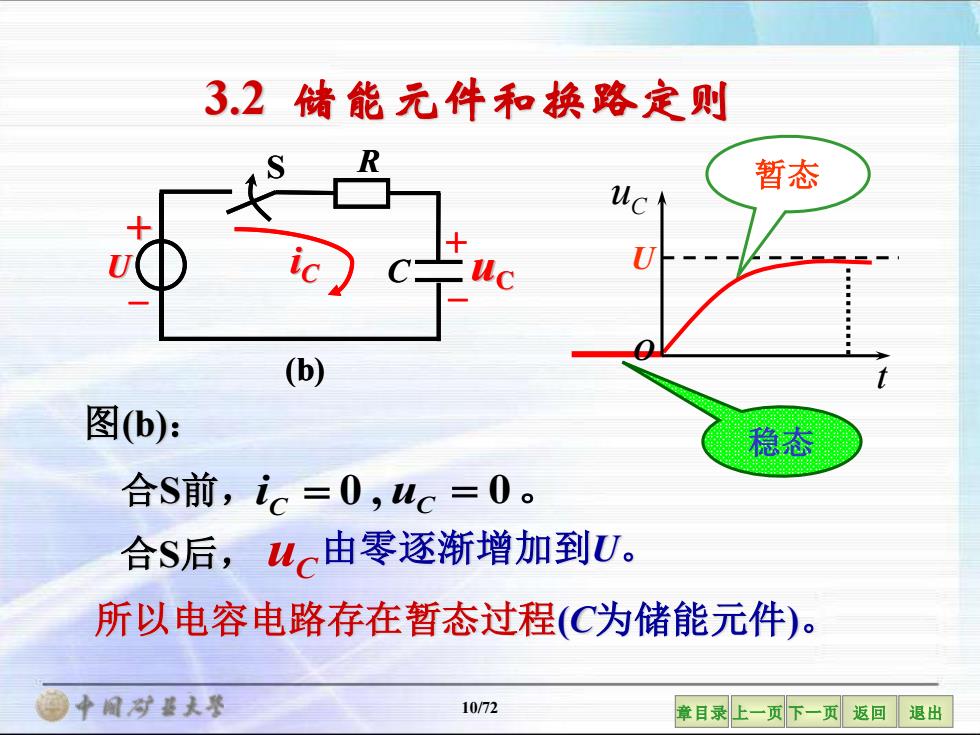
3.2储能元件和换路定则暂态 (b) 图b): 稳态合S前，ic=0,uc=0。合S后，uc由零逐渐增加到U。所以电容电路存在暂态过程(C为储能元件)。酒中间对整大琴 10/72 章目录上一页下一页返回退出

10/72 章目录上一页下一页返回退出 3.2 储能元件和换路定则图(b)：合S后， uC 由零逐渐增加到U。所以电容电路存在暂态过程(C为储能元件)。 = 0 , C 合S前， i uC = 0。 U 暂态稳态 O t C u uC + – iC C (b) U + – S R uC + – iC C (b) U + – S R

点击进入文档下载页（PPT格式）

共72页，可试读20页，点击继续阅读 ↓↓

点击下载（PPT格式）

浏览记录