
第3章电路的暂态分析 WXH WXH 电路的暂态分析,就是当电路外加电源或在初 始储能作用下,以及电路工作状态改变时,求解电 路中电流、电压随时间的变化规律。 如果电路中只含有一个独立的储能元件,则电 路方程是一阶常系数线性微分方程。用一阶微分方 程描述的电路,称为一阶电路。 电路的暂态本质是能量的再分配。 四区
WXH WXH 1 第3章电路的暂态分析

WXH 本章用经典法在时间领域内对动态电路进行分 析和计算(所以又称时域分析法),主要内容有: (1)换路定则和电路初始状态的计算 (2)一阶电路的零输入响应和零状态响应 (3)一阶电路的全响应及三要素公式 (4)微分电路与积分电路
WXH WXH 2

说明: WXH X田 2年025 讲课重点:直流电路、交流电路都存在过渡过程。 我们讲课的重点是直流电路的过渡过程。 研究过渡过程的意义:过渡过程是一种自然现象, 有利有弊。有利的方面,如电子技术中常用它来产 生各种波形;不利的方面,如在暂态过程发生的瞬 间,可能出现过压或过流,致使设备损坏,必须采 取防范措施。 囚
WXH WXH 3 讲课重点:直流电路、交流电路都存在过渡过程。 我们讲课的重点是直流电路的过渡过程。 研究过渡过程的意义:过渡过程是一种自然现象, 有利有弊。有利的方面,如电子技术中常用它来产 生各种波形;不利的方面,如在暂态过程发生的瞬 间,可能出现过压或过流,致使设备损坏,必须采 取防范措施。 说明:

3.l.电阻元件、电感元件(inductor)与电容元件(capacitor) WXH 3.1.1.电阻元件 特点: 时刻服从欧姆定律 耗能元件 ★
WXH WXH 4 3.1. 电阻元件、电感元件 (inductor)与电容元件(capacitor) 3.1.1.电阻元件 特点: 时刻服从欧姆定律 耗能元件
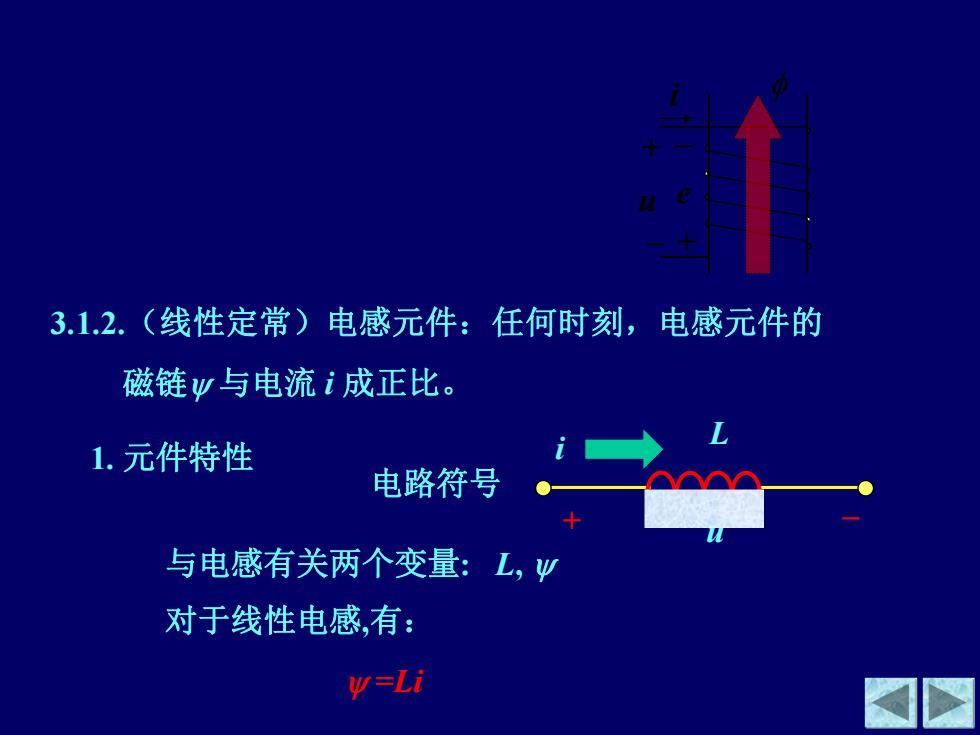
3.1.2.(线性定常)电感元件:任何时刻,电感元件的 磁链w与电流i成正比。 1.元件特性 电路符号 与电感有关两个变量:L,w 对于线性电感,有: w=Li
与电感有关两个变量: L, 对于线性电感,有: =Li i + –u –+ e 3.1.2.(线性定常)电感元件:任何时刻,电感元件的 磁链 与电流 i 成正比。 L i u + – 电路符号 1. 元件特性

defΨ V=NΦ为电感线圈的磁链 L称为自感系数 电感L的单位:H(亨)(Henry,亨利 H=Wb/A=Vs/A=Qs 线性电感的世~特性是过原点的直线 L=w/i octga
线性电感的 ~i 特性是过原点的直线 O i L= /i tg =N 为电感线圈的磁链 L 称为自感系数 电感 L 的单位:H(亨) (Henry,亨利) H=Wb/A=V•s/A=•s
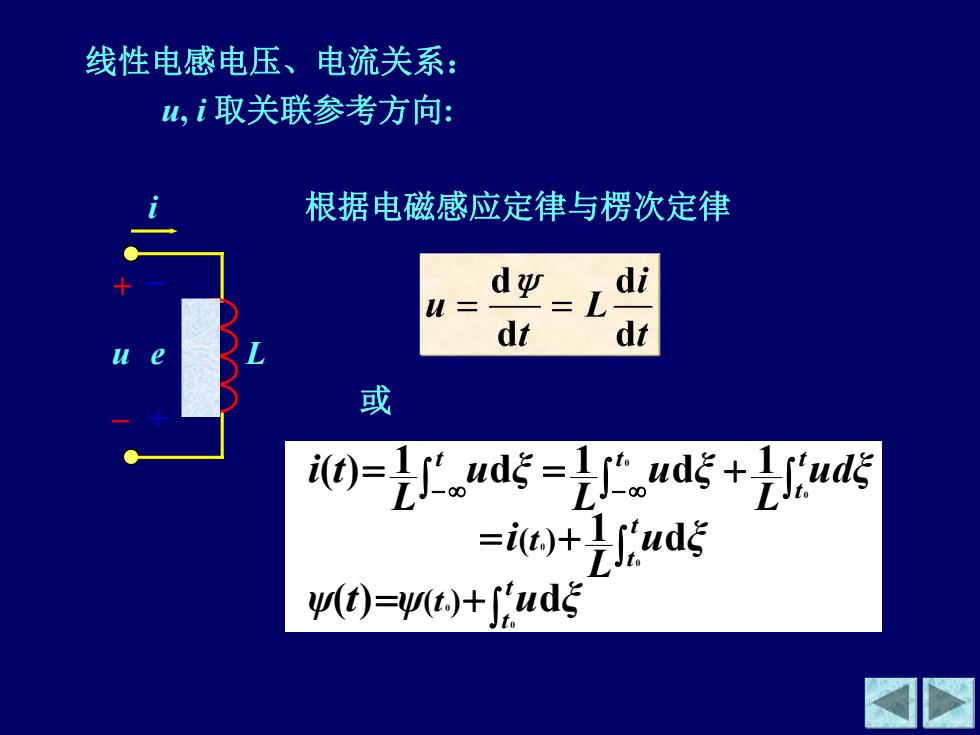
线性电感电压、电流关系: 山,i取关联参考方向: 根据电磁感应定律与楞次定律 d亚 di u= dt dt 或 ()=Iud-Iud +uds -it)+uds )=)+ud5
线性电感电压、电流关系: u, i 取关联参考方向: L i u + – e + – 根据电磁感应定律与楞次定律 或 t t t t t t t t ψ t ψ u ξ u ξ L i udξ L u ξ L u ξ L i t t t 0 0 0 0 0 0 ( ) d 1 d ( ) 1 d 1 d 1 ( ) ( )

讨论金 ()的大小取决与i的变化率,与i的大小无关; (微分形式) (②)电感元件是一种记忆元件;(积分形式) (3)当i为常数(直流)时,di/dt=0-→u=0。 电感在直流电路中相当于短路; (④)表达式前的正、负号与,i的参考方向有关。当 u,为关联方向时,u=Ldi/dt; u,为非关联方向时,u=-Ldi/dt
讨论: (1) u的大小取决与 i 的变化率,与 i 的大小无关; (微分形式) (2) 电感元件是一种记忆元件;(积分形式) (3) 当 i 为常数(直流)时,di/dt =0 u=0。 电感在直流电路中相当于短路; (4) 表达式前的正、负号与u,i 的参考方向有关。当 u,i为关联方向时,u=Ldi/dt; u,i为非关联方向时,u= –Ldi/dt

2.电感的储能 P吸=ui=i:L di dt =4g=re0-w -1L()= 742(t))≥0 2 从到t电感储能的变化量: 由此可以看出,电感是无源元件,它本身不消耗能量
2. 电感的储能 由此可以看出,电感是无源元件,它本身不消耗能量。 从t0 到t 电感储能的变化量: ( ) 2 1 ( ) 2 1 ( ) 2 1 ( ) 2 1 0 2 2 0 2 2 ψ t L ψ t L W Li t Li t L t i p ui i L d d 吸 ( ) 0 2 1 ( ) 2 1 ( ) 2 1 ( ) 2 1 ( ) 2 1 d d d 2 2 ( ) 0 2 2 2 ψ t L Li t ξ Li Li t Li i W Li i t t L 若 ξ ξ
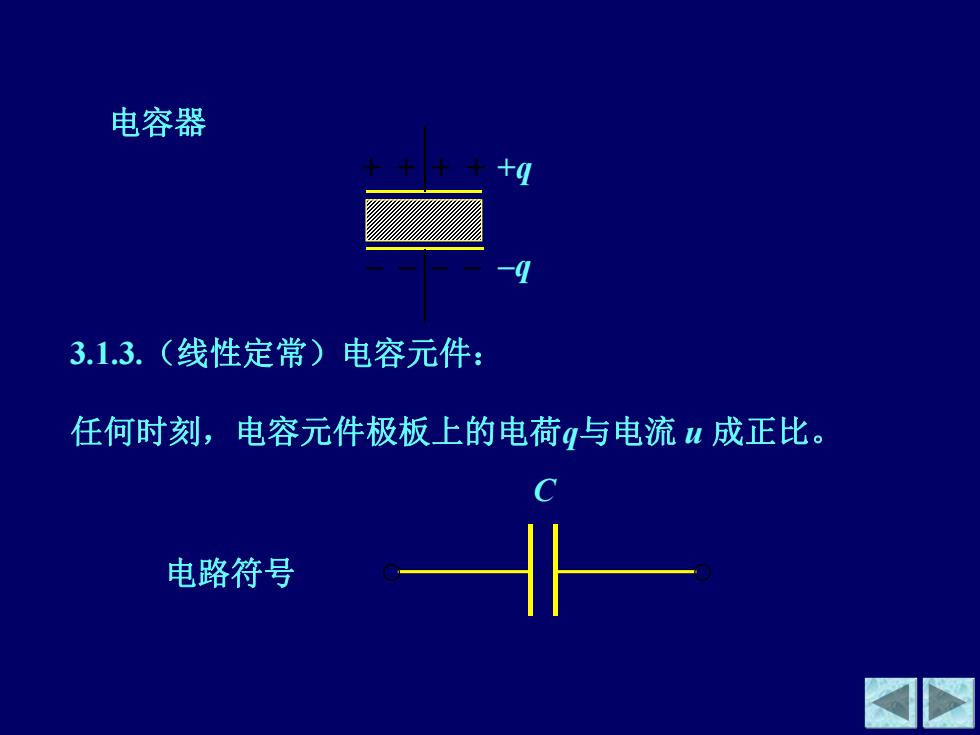
电容器 +0 3.1.3.(线性定常)电容元件: 任何时刻,电容元件极板上的电荷与电流成正比。 C 电路符号
3.1.3.(线性定常)电容元件: 任何时刻,电容元件极板上的电荷q与电流 u 成正比。 电路符号 电容器 + + + + – – – – +q –q C