
第八章工厂照明 本章提要: 照明(illumination)是人类文明的象征。良好的 照明是保证安全生产、提高劳动效率、保护视看者 视力健康、创造舒适环境的必要条件。为了获得良 好的照明必需有合理的照明设计,合理的照明设计 应符合适用、安全、保护视力和经济的要求。 本章着重介绍 ◆照明光源(light source)和灯具(lamps and lanterns)的性能及选择, ◆灯具布置, ◆照度(illuminance)计算 ◆照明设计方法
照明(illumination )是人类文明的象征。良好的 照明是保证安全生产、提高劳动效率、保护视看者 视力健康、创造舒适环境的必要条件。为了获得良 好的照明必需有合理的照明设计,合理的照明设计 应符合适用、安全、保护视力和经济的要求。 第八章 工 厂 照 明 本章提要: 本章着重介绍 ◆照明光源(light source)和灯具(lamps and lanterns)的性能及选择, ◆灯具布置, ◆照度(illuminance )计算 ◆照明设计方法

§6-1照明概述 一、光(ray) 光(ray)是我们生活、工作和学习必不可少的,它是一种电 磁辐射(eiectromagnetic radiation)。光波(light wave)在整个 电磁波谱中只占据很小的部分(见图6-1).光波的波长区间从 几个纳米(nm(1n10-9m到1毫米(mm左右.这些光并不是 都能看得见,人眼所能看见的只是其中一部分,我们将这一 部分光称为可见光(visible light),它的波长在380nr780 nm之间,在可见光中,波长最短的(约380n435nm)是 紫光,波长最长的(约630nm~780nm)是红光。在不可见 光中,波长比紫光短的部分称为紫外线(ultraviolet ro心), 比红光长的叫做红外线(infrared re)
光(ray)是我们生活、工作和学习必不可少的,它是一种电 磁辐射(eiectromagnetic radiation)。光波(light wave)在整个 电磁波谱中只占据很小的部分(见图6-1).光波的波长区间从 几个纳米(nm)(1nm=10-9m)到1毫米(mm)左右.这些光并不是 都能看得见,人眼所能看见的只是其中一部分,我们将这一 部分光称为可见光(visible light),它的波长在380 nm~ 780 nm之间,在可见光中,波长最短的(约380 nm~ 435 nm)是 紫光,波长最长的(约630 nm ~780 nm)是红光。在不可见 光中,波长比紫光短的部分称为紫外线(ultraviolet ray ), 比红光长的叫做红外线(infrared ray )。 §6-1 照明概述 一、光(ray)

紫蓝绿黄红 100 200 300400500600700800 106 A(nm) 紫外 可见光 红外 Y射线 X射线 雷达一电视一无线电一电力 10-1410-1210-1010-810610-410-210102104 2(m) 图8-1 电磁光谱
l(nm) 雷达—电视—无线电—电力 104 102 10 10 -2 10-4 10-6 10-8 10-10 10-12 10-14 100 200 300 400 500 600 700 800 可见光 g 射线 X射线 紫外 红外 紫 蓝 绿 黄 红 图8-1 电磁光谱 106 l(m) l(nm) 雷达—电视—无线电—电力 104 102 10 10 -2 10-4 10-6 10-8 10-10 10-12 10-14 100 200 300 400 500 600 700 800 可见光 g 射线 X射线 紫外 红外 紫 蓝 绿 黄 红 图8-1 电磁光谱 106 l(m) l(nm) 雷达—电视—无线电—电力 104 102 10 10 -2 10-4 10-6 10-8 10-10 10-12 10-14 100 200 300 400 500 600 700 800 可见光 g 射线 X射线 紫外 红外 紫 蓝 绿 黄 红 图6-1 电磁光谱 106 l(m)

辐射度量∠ 不考虑人的视觉效果的、纯客观的物理量 二、光的度量 光度量 在照明工程中经常使用的物理量 1.光通量(luminous flux) 某物体在单位时间内发射或接收的辐射能量称为辐射通量,或称辐 射功率P,单位瓦(W)。 光源是向周围空间辐射能量的,而 表8-1常用光源的光通量 使人眼产生光感的辐射通量,称为 光源种类 光通量/lm 光通量,用符号Φ表示,单位为流 荧光灯(40W) 2400 明(亿m。光通量与光源的辐射功率 荧光灯(100W) 5500 的强弱有关,它是说明光源发光能 白炽灯(40W) 350 卤钨灯(500W) 10500 力的基本物理量,某些特定光源的 光通量列于表8-1中
1.光通量(luminous flux) 某物体在单位时间内发射或接收的辐射能量称为辐射通量,或称辐 射功率P,单位瓦(W)。 二、光的度量 表8-1 常用光源的光通量 光源种类 光通量/ lm 荧光灯(40W) 2400 荧光灯(100W) 5500 白炽灯(40W) 350 卤钨灯(500W) 10500 光源是向周围空间辐射能量的,而 使人眼产生光感的辐射通量,称为 光通量,用符号Φ表示,单位为流 明(lm)。光通量与光源的辐射功率 的强弱有关,它是说明光源发光能 力的基本物理量,某些特定光源的 光通量列于表8-1中。 辐射度量 光度量 不考虑人的视觉效果的、纯客观的物理量 在照明工程中经常使用的物理量
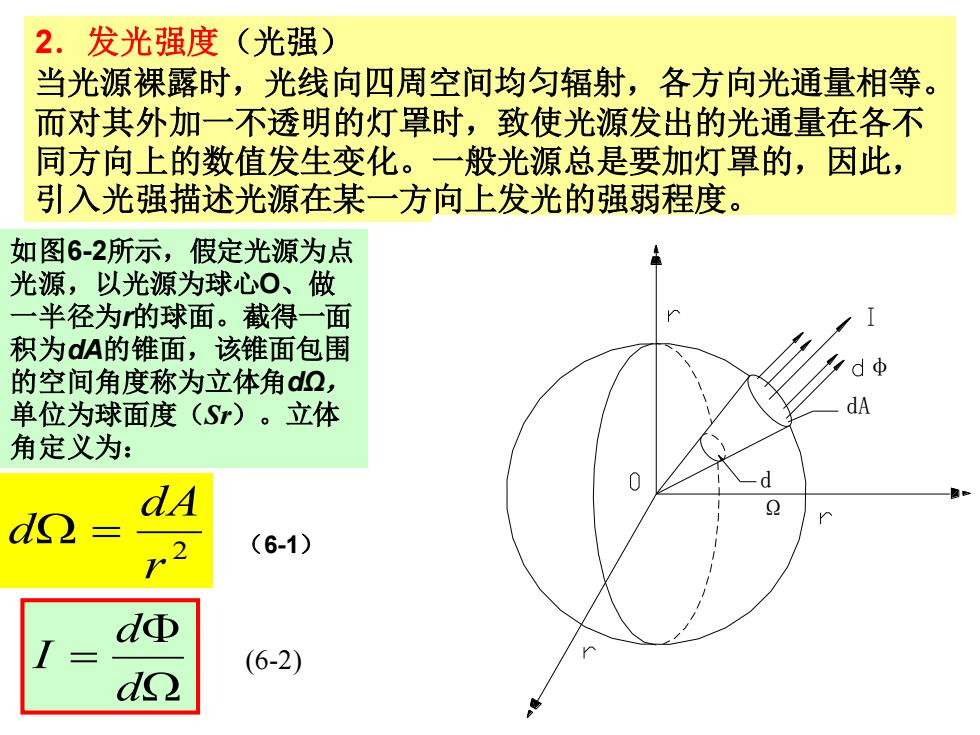
2.发光强度(光强) 当光源裸露时,光线向四周空间均匀辐射,各方向光通量相等。 而对其外加一不透明的灯罩时,致使光源发出的光通量在各不 同方向上的数值发生变化。一般光源总是要加灯罩的,因此, 引入光强描述光源在某一方向上发光的强弱程度。 如图6-2所示,假定光源为点 光源,以光源为球心O、做 一半径为的球面。截得一面 积为dA的锥面,该锥面包围 dφ 的空间角度称为立体角dQ, 单位为球面度(S)。立体 dA 角定义为: dg (6-1) dΦ (6-2)
2.发光强度(光强) 当光源裸露时,光线向四周空间均匀辐射,各方向光通量相等。 而对其外加一不透明的灯罩时,致使光源发出的光通量在各不 同方向上的数值发生变化。一般光源总是要加灯罩的,因此, 引入光强描述光源在某一方向上发光的强弱程度。 2 r dA d = φ dA d Ω 如图6-2所示,假定光源为点 光源,以光源为球心O、做 一半径为r的球面。截得一面 积为dA的锥面,该锥面包围 的空间角度称为立体角dΩ, 单位为球面度(Sr)。立体 角定义为: (6-1) = d d I (6-2)

例6-1100W普通白炽灯辐射光通量为1250lm,假设光源向 四周辐射的光通量是均匀的,求光源某方向上的光强。 解:根据题意,光源向四周辐射的光通量是均匀的,因 此在任一方向上的光强也是相等的,故可以光源为球心, 作一半径为的球面,球面积4π2,其立体角为 4m2 =4πSr 1250 故各方向光强为 cd=99.5cd 4π
例6-1 100W普通白炽灯辐射光通量为1250lm,假设光源向 四周辐射的光通量是均匀的,求光源某方向上的光强。 解: 根据题意,光源向四周辐射的光通量是均匀的,因 此在任一方向上的光强也是相等的,故可以光源为球心, 作一半径为r的球面,球面积4πr 2,其立体角为 故各方向光强为 4 4 2 2 2 = = = r r r A Sr cd=99.5cd 4 1250 = I =
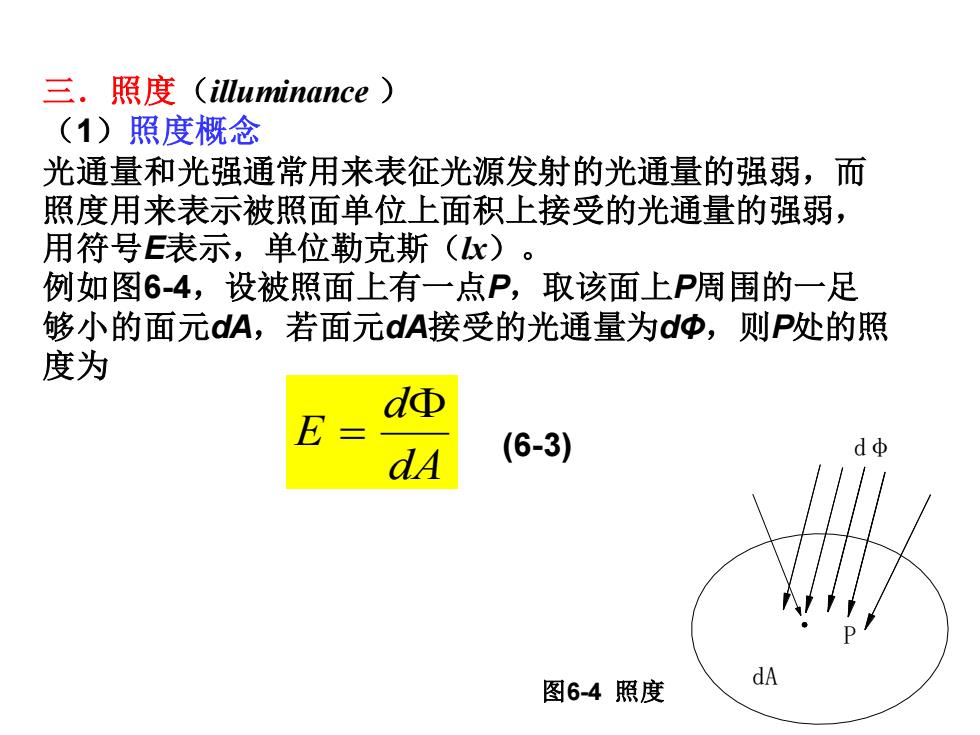
三.照度(illuminance) (1)照度概念 光通量和光强通常用来表征光源发射的光通量的强弱,而 照度用来表示被照面单位上面积上接受的光通量的强弱, 用符号E表示,单位勒克斯(x)。 例如图6-4,设被照面上有一点P,取该面上P周围的一足 够小的面元dA,若面元dA接受的光通量为dΦ,则P处的照 度为 dΦ dA (6-3) dΦ 图6-4照度
三.照度(illuminance ) (1)照度概念 光通量和光强通常用来表征光源发射的光通量的强弱,而 照度用来表示被照面单位上面积上接受的光通量的强弱, 用符号E表示,单位勒克斯(lx)。 例如图6-4,设被照面上有一点P,取该面上P周围的一足 够小的面元dA,若面元dA接受的光通量为dΦ,则P处的照 度为 (6-3) dA d E = dA P dφ 图6-4 照度

例题: 100W普通白炽灯辐射光通量为1250lm,假设光 源向四周辐射的光通量是均匀的,求灯下2m处的 照度值。 解:仍以点光源为球心作半径为2的球面,球面内侧接收 的光通量也是均匀的,故球面内侧的照度为 Φ Φ 1250 E- A 2 1x=24.91x 4 4π×22
例题: 100W普通白炽灯辐射光通量为1250lm,假设光 源向四周辐射的光通量是均匀的,求灯下2m处的 照度值。 2 2 4 2 1250 4 = = = A r E lx=24.9lx 解: 仍以点光源为球心作半径为2m 的球面,球面内侧接收 的光通量也是均匀的,故球面内侧的照度为

(2)光强与照度的关系 光源光强已知,它在任意方向某平面上形成的照度可由以下两 定律决定。 1)距离平方反比定律 当光源的直径小于它至被照面距离的1/5时,则可把该光源视 为点光源。 设有点光源位于半径为的球心,该光源向各方向均匀发光, 光强为I总光通量为Φ=4πI,则球的内表面各点的照度E为 Φ 4πd E= A 42
(2)光强与照度的关系 光源光强已知,它在任意方向某平面上形成的照度可由以下两 定律决定。 1)距离平方反比定律 当光源的直径小于它至被照面距离的1/5时,则可把该光源视 为点光源。 设有点光源位于半径为r的球心,该光源向各方向均匀发光, 光强为I总光通量为Φ=4πI,则球的内表面各点的照度E为 2 2 4 4 r I r I A E = = =

2)入射角余弦定律 如图6-5(b)所示,有一面积为A的平面A1,接受与平面成垂直方 向射来的光通量为中,则该平面的照度 Φ 今假定将此平面倾斜一个角度得面A,于是射入该平面的光通 量将变成Φcos0,因此该平面上的照度应为: Φcosθ Ee E,cos A 即任意平面的照度,与光线入射角(入射光的方向与平面法线 之间的夹角)的余弦成正比。这就是所谓入射角余弦定律
2)入射角余弦定律 如图6-5(b)所示,有一面积为A的平面A1,接受与平面成垂直方 向射来的光通量为Φ,则该平面的照度 A En = cos cos En A E = = 今假定将此平面倾斜一个角度θ得面A2,于是射入该平面的光通 量将变成Φcosθ,因此该平面上的照度应为: 即任意平面的照度,与光线入射角(入射光的方向与平面法线 之间的夹角)的余弦成正比。这就是所谓入射角余弦定律