烟台理工学院：《自动控制原理》课程教学资源（课件讲稿）第二章 控制系统的数学模型（拉氏变换）

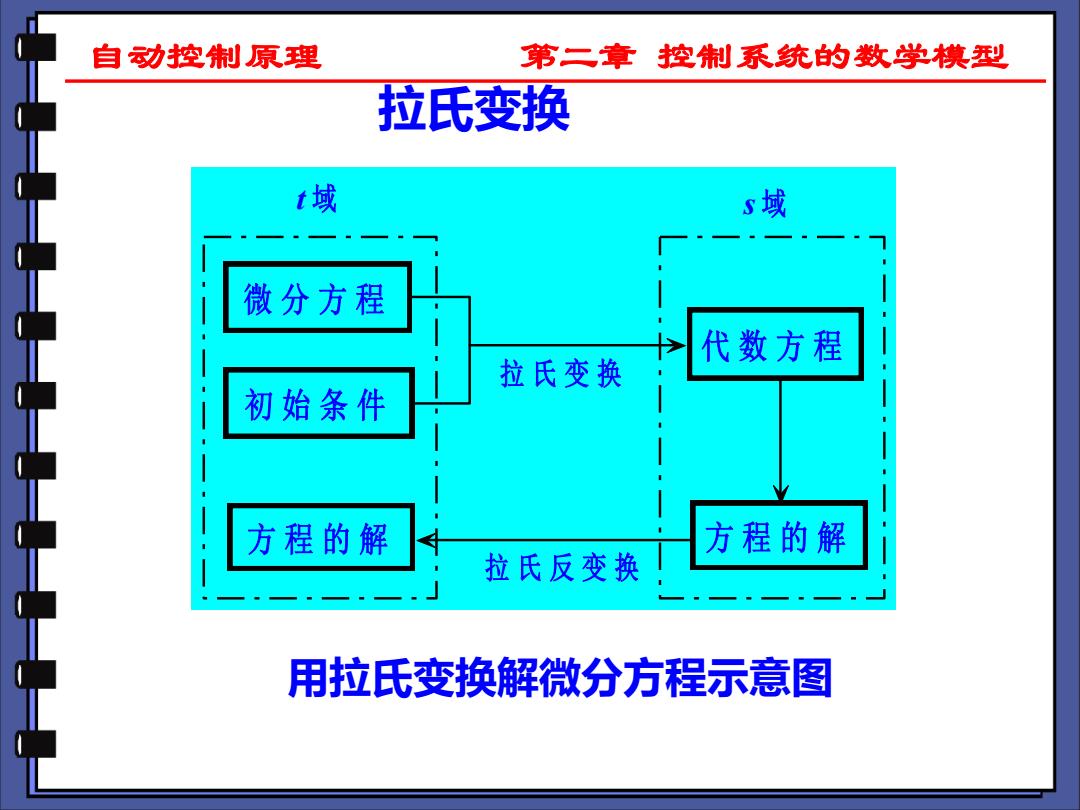
自动控制原理 第二章控制系统的数学模型 拉氏变换 t域 s域 微分方程 代数方程 拉氏变换 初始条件 方程的解 方程的解 拉氏反变换 用拉氏变换解微分方程示意图

自动控制原理 第二章 控制系统的数学模型 微 分 方 程 初 始 条 件 方 程 的 解 代 数 方 程 方 程 的 解 拉 氏 变 换 拉 氏 反 变 换 t 域 s 域 用拉氏变换解微分方程示意图 拉氏变换

自动控制原理 第二章控制系统的数学模型 拉氏变换的定义 1.定义 设函数孔)在20时有定义，如果线性积分 ∫fue"a (5=σ+jo,0>0) 存在，则由此积分所确定的函数可写为 F(s)=f(t)e"dt 见课本P26式(2-11)}

自动控制原理 第二章 控制系统的数学模型 一 、 拉氏变换的定义 1. 定义 设函数f(t)在t≥0时有定义，如果线性积分 0 ( )e dst f t t + −  ( , 0) s = +     j 存在，则由此积分所确定的函数可写为 - 0 ( ) ( )e dst F s f t t + =  {见课本P26 式（2-11）}

自动控荆原理 第二章控制系统的数学模型 称其为函数孔)的拉普拉斯变换，并记作 F(s)=LLf(t) 代S)称为的象函数，而孔)称为尺S的原函数， 由象函数求原函数的运算称为拉氏反变换，记作 f(t)=LF(s)] {见课本P26式(2-12)}

自动控制原理 第二章 控制系统的数学模型 F s L f t ( ) [ ( )] = L F(s)称为f(t)的象函数，而f(t)称为F(s)的原函数， 由象函数求原函数的运算称为拉氏反变换，记作 1 f t L F s ( ) [ ( )] − = 称其为函数f(t)的拉普拉斯变换，并记作 {见课本P26 式（2-12）}

自动控制原理 第二章控制系统的数学模型 二、几种典型函数的拉氏变换(P32表2-3) 1.单位阶跃函数1() )个 数学表达式为 0=0= 0 其拉氏变换为 Fs)=L【f(tI=Jft)edt =小1e=elg=-0-川=月

自动控制原理 第二章 控制系统的数学模型 二、几种典型函数的拉氏变换(P32 表2-3) 1.单位阶跃函数1(t) 数学表达式为 其拉氏变换为 O t f(t) 1 0 0 0 ( ) [ ( )] ( )e d 1 1 1 1 e d e [0 1] st st st F s f t f t t t s s s + − + − − + = = =  = − = − − =   L 1 0 ( ) 1( ) 0 0 t f t t t  = =    ≥

自动控制原理 第二章控制系统的数学模型 4.指数函数em 数学表达式为 四日！o的安 0 t<0 其拉氏变换为 F()=L[e"]=∫ee dt =∫= 1 s+a

自动控制原理 第二章 控制系统的数学模型 4.指数函数e -at 数学表达式为 其拉氏变换为 e 0( ) ( ) 0 0 at t a f t t −  =    ≥ 为实数 0 ( ) 0 ( ) e e e d 1 e d at at st s a t F s t t s a + − − − + − + = =     = = +   L

自动控制原理 第二章控制系统的数学模型 5.正弦函数sinot (P26例题2-3) 正弦函数定义为 sinot t≥0 t=0 t<0 其拉氏变换为 F(s)=L [sin ot]=sinote-"dt =小2（em-e)e

自动控制原理 第二章 控制系统的数学模型 5.正弦函数sint （P26例题2-3） 正弦函数定义为 sin 0 sin 0 0 t t t t    =    ≥ 其拉氏变换为 ( ) 0 j j 0 2 2 ( ) [sin ] sin e d 1 e e e d 2 j 1 1 1 2j j j st t t st F s t t t t s s s         + − + − − = = = −   = − =     − + +   L

自动控制原理 第二章控制系统的数学模型 6.单位脉冲函数（涵数）例题2-4 6函数的表达式为 且δt)dt=1 其拉氏变换为 F(w)=4δ=J0δu)e“dt=1 P27中间，不特别指出时，拉氏积分下限均为0

自动控制原理 第二章 控制系统的数学模型 6. 单位脉冲函数(函数) 例题2-4  函数的表达式为 0 ( ) ( )d 1 0 0 t t t t t   + −  = = =     且 O t (t) 其拉氏变换为 0 ( ) [ ( )] ( )e d 1 st F s t t t   − + − = = =  L P27中间，不特别指出时，拉氏积分下限均为0-

自动控制原理 第二章控制系统的数学模型 三、拉氏变换定理 1.线性性质 设F(s)=L[f,F2(s)=L[f(,a和b为常 数，则有 L[af (t)+bf (t)]=aF (s)+bF2(s)

自动控制原理 第二章 控制系统的数学模型 三、拉氏变换定理 1.线性性质 设F1 (s)=L [ f1 (t)]，F2 (s)=L [ f2 (t)]，a和b为常 数，则有 1 2 1 2 L af t bf t aF s bF s [ ( ) ( )] ( ) ( ) + = +

自动控荆原理 第二章控制系统的数学模型 2.微分定理 设F(s)=LLf)小，则有 式中：f0),f0),为f)及其一阶导数在=0处的值。 一阶微分：L[f'()]=sF(s)-f(0) 二阶微分：L[f"()]=s2F(s)-f(0)-f'(0)

自动控制原理 第二章 控制系统的数学模型 2.微分定理 设F(s)=L [ f(t)]，则有 L f t sF s f  ( ) ( ) (0)  = −   2 L f t s F s sf f   ( ) ( ) (0) (0) = − − 式中：f(0), f(0), 为f(t)及其一阶导数在t=0处的值。 一阶微分： 二阶微分：

自动控荆原理 第二章控制系统的数学模型 当f0)=f'0)=f”(0)=…=fm-(0)=0时的微分法则： LIf((t)]=s"F(s) 此时， d s dt 即零初始条件下，时域中的微分运算对等于复 数域中乘以s的运算

自动控制原理 第二章 控制系统的数学模型 当 时的微分法则： ( ) [ ( )] ( ) n n L f t s F s = 此时， d s dt 即零初始条件下，时域中的微分运算对等于复 数域中乘以s的运算。 ( 1) (0) (0) (0) (0) 0 n f f f f − = = = = =  