重庆大学：《电机学》课程教学资源（PPT课件）电机不对称运行

不对称问题分析方法与应用 。1。对称分量法的基本原理（汤书258） -1.1三相对称系统的概念、表达，不对称问题引入 -1.2不对称与对称系统的转换一一对称分量法 -1.3物理解释 ·2。对称分量法应用 2.1椭圆形磁场分析 -2.2单相感应电动机原理分析 - 2.3三相变压器不对称运行分析 2.4同步发电机不对称运行分析

一。不对称问题分析方法与应用 ⚫ 1。对称分量法的基本原理(汤书p258) – 1.1 三相对称系统的概念、表达，不对称问题引入 – 1.2 不对称与对称系统的转换－－对称分量法 – 1.3 物理解释 ⚫ 2。对称分量法应用 – 2.1 椭圆形磁场分析 – 2.2 单相感应电动机原理分析 – 2.3 三相变压器不对称运行分析 – 2.4 同步发电机不对称运行分析

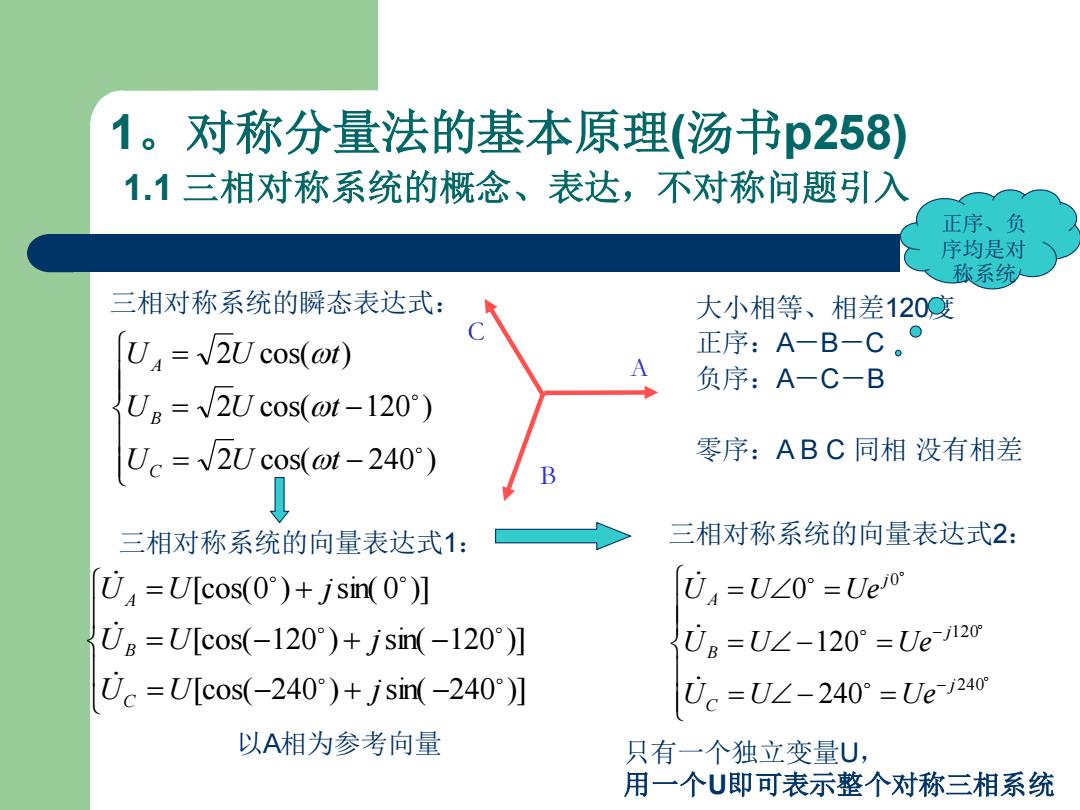
1。对称分量法的基本原理（汤书p258) 1.1三相对称系统的概念、表达，不对称问题引入 正序、负 序均是对 称系统 三相对称系统的瞬态表达式： 大小相等、相差120度 U4=√2Ucos(o)） 正序：A-B-C。° 负序：A一C一B UB=V2Ucos(ot-120°) Uc=2U cos(@t-240) 零序：ABC同相没有相差 三相对称系统的向量表达式1： 三相对称系统的向量表达式2： U=U[cos(0)+jsin(0)] U4=U∠0°=Ue1o 0B=U[cos(-120)+jsm(-120°] 0。=U∠-120°=Ue120 Uc=U[cos(-240)+jsin(-240】 Uc=U∠-240°=Ue240 以A相为参考向量 只有一个独立变量U, 用一个U即可表示整个对称三相系统

1。对称分量法的基本原理(汤书p258) 1.1 三相对称系统的概念、表达，不对称问题引入 三相对称系统的瞬态表达式：        = − = − = 2 cos( 240 ) 2 cos( 120 ) 2 cos( )   U U t U U t U U t C B A    A B 三相对称系统的向量表达式1：      = − + − = − + − = + [cos( 240 ) sin( 240 )] [cos( 120 ) sin( 120 )] [cos(0 ) sin( 0 )]          U U j U U j U U j C B A 以A相为参考向量 三相对称系统的向量表达式2：        = − = = − = =  = − −          240 120 0 240 120 0 j C j B j A U U Ue U U Ue U U Ue 只有一个独立变量U， 用一个U即可表示整个对称三相系统 大小相等、相差120度 正序：A－B－C 负序：A－C－B 零序：A B C 同相 没有相差 正序、负 序均是对 称系统

1。对称分量法的基本原理（汤书p258) 1.1三相对称系统的概念、表达，不对称问题引入 引入复数算子a:a=e120 则三相对称系统的向量表达式 复数算子a的一些特性 B 0,=U∠0°=Ue0=aU a=e120=ej240 0g=U∠-120°=Ue12r=a20 a2=e1240=ej120 0 =U∠-240°=Ue24w=aU 度+或U-或0 a3=e1360=e0°=1 只有一个独立向量U,。 用一个向量u即可表示整个对称三相系=c0s(120°)+jSin(120)=e120 1111I

1。对称分量法的基本原理(汤书p258) 1.1 三相对称系统的概念、表达，不对称问题引入        = − = = = − = = =  = = − − U U Ue aU U U Ue a U U U Ue a U j C j B j A             240 120 2 0 0 240 120 0 则三相对称系统的向量表达式 引入复数算子a：  j120 a = e 复数算子a的一些特性          120 3 360 0 2 240 120 120 240 cos(120 ) sin(120 ) 1 j j j j j j j a j e a e e a e e a e e = + = = = = = = = = − − 只有一个独立向量U， 用一个向量U即可表示整个对称三相系统 ！！！！！ U U U0  +或  −或  A B

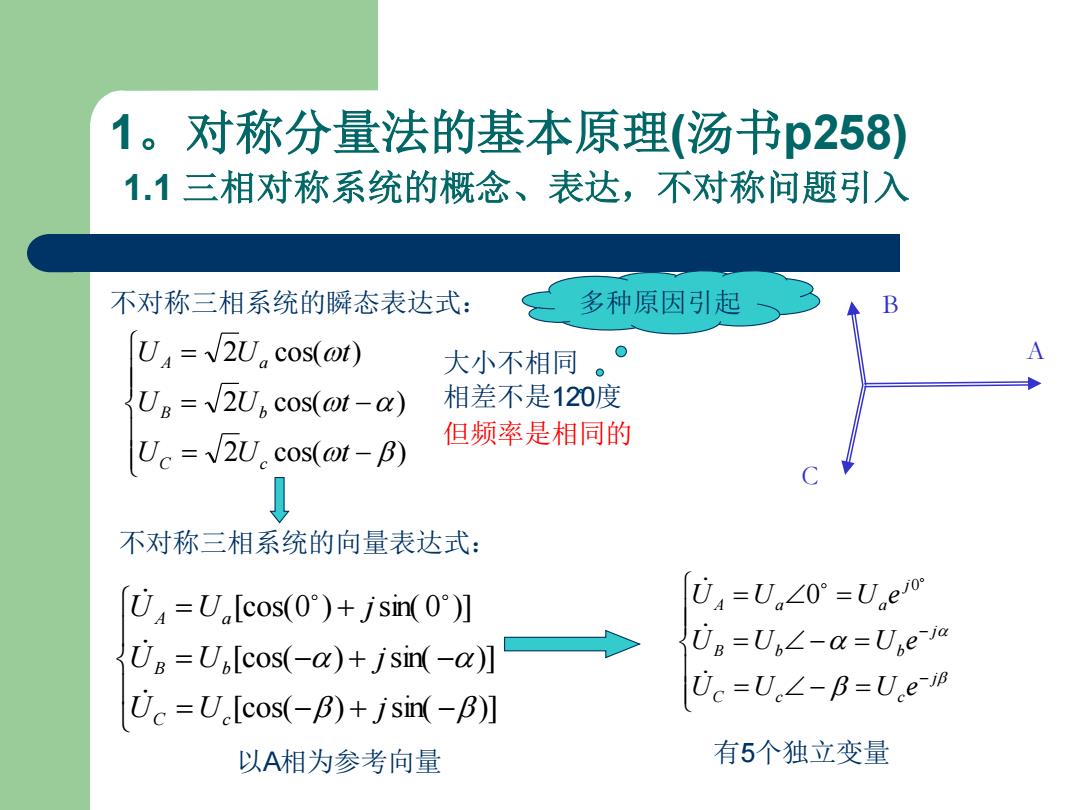
1。对称分量法的基本原理（汤书p258) 1.1三相对称系统的概念、表达，不对称问题引入 不对称三相系统的瞬态表达式： 多种原因引起 U=2Ucos(@t) 大小不相同 。0 Ug=2U,cos(@t-a) 相差不是120度 Uc=2U.cos(@t-B) 但频率是相同的 ↓ 不对称三相系统的向量表达式： U=U[cos(0)+jsin()] 04=Un∠0°=U,e0 Ug =U[cos(-a)+jsin(-a)] Ug=Ub∠-a=Uea 0c=U.∠-B=U.eB Uc=U.[cos(-B)+jsin(-B)] 以A相为参考向量 有5个独立变量

1。对称分量法的基本原理(汤书p258) 1.1 三相对称系统的概念、表达，不对称问题引入 不对称三相系统的瞬态表达式：        = − = − = 2 cos( ) 2 cos( ) 2 cos( )      U U t U U t U U t C c B b A a 不对称三相系统的向量表达式：      = − + − = − + − = + [cos( ) sin( )] [cos( ) sin( )] [cos(0 ) sin( 0 )]     U U j U U j U U j C c B b A a             = − = = − = =  = − −     j C c c j B b b j A a a U U U e U U U e U U U e      0 0 以A相为参考向量 有5个独立变量 大小不相同 相差不是120度 但频率是相同的 多种原因引起 A B C

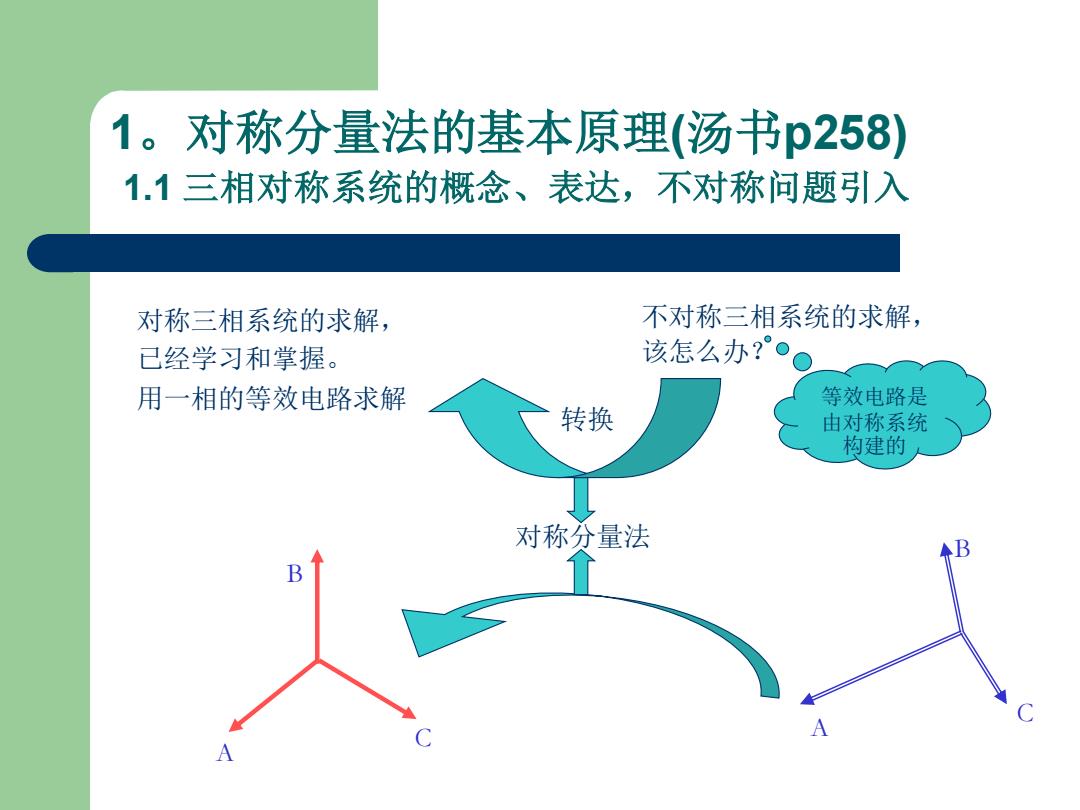
1。对称分量法的基本原理（汤书p258) 1.1三相对称系统的概念、表达，不对称问题引入 对称三相系统的求解， 不对称三相系统的求解， 已经学习和掌握。 该怎么办？°。 用一相的等效电路求解 等效电路是 转换 由对称系统 构建的 对称分量法 ◆B

1。对称分量法的基本原理(汤书p258) 1.1 三相对称系统的概念、表达，不对称问题引入 对称三相系统的求解， 已经学习和掌握。 用一相的等效电路求解 不对称三相系统的求解， 该怎么办？ 转换 对称分量法 A B C A B C 等效电路是 由对称系统 构建的

1。对称分量法的基本原理（汤书p258) 1.2不对称与对称系统的转换一一对称分量法 要求解不对称三相系统，就需要将不对称转换为对称系统 转换的方法：对称分量法： 转换的思想：把不对称的三相系统分解为相序分别为正、负、零的三个独 立的对称系统的叠加 三个独立变量+两个相对角度变量 转换的思路： a。假设有独立对称系统U+,U一，Uo,其叠加正构成不对称三相系统； b。 如果能找到这三个对称系统的表达式，则假设成立； c。相应的，不对称的三相系统也就分解城了三个独立的对称系统U+,U一， Uo

1。对称分量法的基本原理(汤书p258) 1.2 不对称与对称系统的转换－－对称分量法 要求解不对称三相系统，就需要将不对称转换为对称系统 转换的方法：对称分量法； 转换的思想：把不对称的三相系统分解为相序分别为正、负、零的三个独 立的对称系统的叠加 转换的思路： a。假设有独立对称系统U+,U－,Uo，其叠加正好构成不对称三相系统； b。如果能够找到这三个对称系统的表达式，则假设成立； c。相应的，不对称的三相系统也就分解成了三个独立的对称系统U+,U－, Uo， 三个独立变量+两个相对角度变量

1。对称分量法的基本原理 1.2不对称与对称系统的转换一一对称分量法 U4=0+0-+00 转换的推导 Un-U +U8+U Uc =Uo:+UE _+Uco U4,心a,Uc构成对称正序系统U U4,0a,Uc构成对称损序系统U Uc构成对称零序系统U

     = + + = + + = + + + − + − + − 0 0 0 C C C C B B B B A A A A U U U U U U U U U U U U             1。对称分量法的基本原理 1.2 不对称与对称系统的转换－－对称分量法 转 换 的 推 导 U 0 U 0 U 0 U0 U U U U U U U U A B C A B C A B C             ， ， 构成对称零序系统 ， ， 构成对称负序系统 ， ， 构成对称正序系统 − − − － + + + +

1。对称分量法的基本原理 1.2不对称与对称系统的转换一一对称分量法 04,U+,0c,构成对称正序系统0→04=U,U=aU,Uc+=a0 04-,0a-,Uc构成对称负序系统U_→04-=U,0。-=aU,0c-=a0 Uo,Uc构成对称零序系统U。→U0=Uo=Uc0=U。 心，=0：-，+k-伯-0+心 UB=UBs+Up-+Umo-aU.+al_+Uo 0c=0c++Uc+0c0=a0,+a20+0

1。对称分量法的基本原理 1.2 不对称与对称系统的转换－－对称分量法      → = → = → = − − − − − − − − − + + + + + + + + + + 0 0 0 0 0 0 0 0 2 2 U U U U U U U U U U U U U U U aU U a U U U U U U U U a U U aU A B C A B C A B C A B C A B C A B C                             ， ， 构成对称零序系统 ＝ ＝ ， ， 构成对称负序系统 ， ＝ ， ＝ ， ， 构成对称正序系统 ， ＝ ， ＝ －      = + + + + = + + + + = + + + + + − + − + − + − + − + − 0 2 0 0 2 0 0 0 U U U U aU a U U U U U U a U aU U U U U U U U U C C C C B B B B A A A A                      ＝ ＝ ＝

1。对称分量法的基本原理 1.2不对称与对称系统的转换一一对称分量法 U U A 文立立 U 1 0 , U 3 Z ABC -(U,+aUg+a-Uc) -3心，+a0+ue） =3心，+0a+0)

1。对称分量法的基本原理 1.2 不对称与对称系统的转换－－对称分量法                      =           − + 0 2 2 1 1 1 1 1 U U U a a a a U U U C B A                            =            − + C B A U U U a a a a U U U       1 1 1 1 1 3 1 2 2 0 +−0 Z ABC          = + + = + + + = + + ( ) 3 1 ( ) 3 1 ( ) 3 1 0 2 2 A B C A B C A B C U U U U U U a U aU U U aU a U             － ABC Z+−0

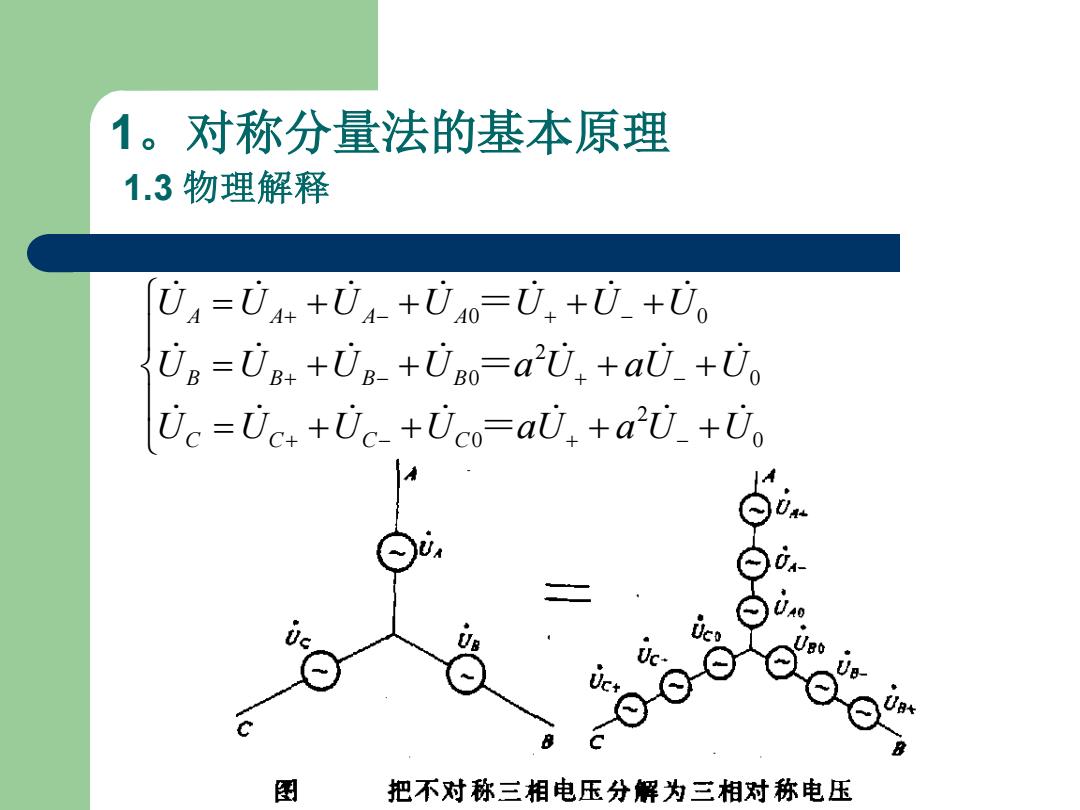
1。对称分量法的基本原理 1.3物理解释 U4=UA4++U4-+U40=U,+U+U。 Ug=Ug:+UB-+Umo-aU:+aU_+Uo Uc=Uc:+Uc-+Uco=al,+aU_+Uo J80 图 把不对称三相电压分解为三相对称电压

1。对称分量法的基本原理 1.3 物理解释      = + + + + = + + + + = + + + + + − + − + − + − + − + − 0 2 0 0 2 0 0 0 U U U U aU a U U U U U U a U aU U U U U U U U U C C C C B B B B A A A A                      ＝ ＝ ＝