
经的) 第七章一阶电路和二阶电路 §7-1 动态电路的方程及其初始状态 §7-2= 阶电路的零输入响应 §7-3一阶电路的零状态响应 §7-4 一阶电路的全响应 96 阶电路的杰响应和全响壶 。子阶跃响应 。子8國
现代制造装备工程技术开发中心 佛山科学技术学院 第七章 一阶电路和二阶电路 §7-1 动态电路的方程及其初始状态 §7-2 一阶电路的零输入响应 §7-3 一阶电路的零状态响应 §7-4 一阶电路的全响应 §7-5 二阶电路的零输入响应 §7-6 二阶电路的零状态响应和全响应 §7-7 阶跃响应 §7-8 冲激响应

第七章一阶电路和二阶电路 §71动态电路的方程及其初始条件 一、电阻电路:由电源和电阻组成的电路 特点:代数方程 二、动态电路:含有动态元件的电路 特点:所列出方程为微分方程 说明: 若R、L、C为线性、非时变元件-线性常系数微分方程 动态电路: 一阶电路:一阶微分方程 二阶电路:三阶微分方程 高阶电路:高阶微分方程
现代制造装备工程技术开发中心 佛山科学技术学院 第七章 一阶电路和二阶电路 、 §7-1 动态电路的方程及其初始条件 一、电阻电路: 由电源和电阻组成的电路 特点:代数方程 二、动态电路: 含有动态元件的电路 特点:所列出方程为微分方程 说明: 若R、L、C为线性、非时变元件---线性常系数微分方程 动态电路: 一阶电路:一阶微分方程 二阶电路:二阶微分方程 高阶电路:高阶微分方程
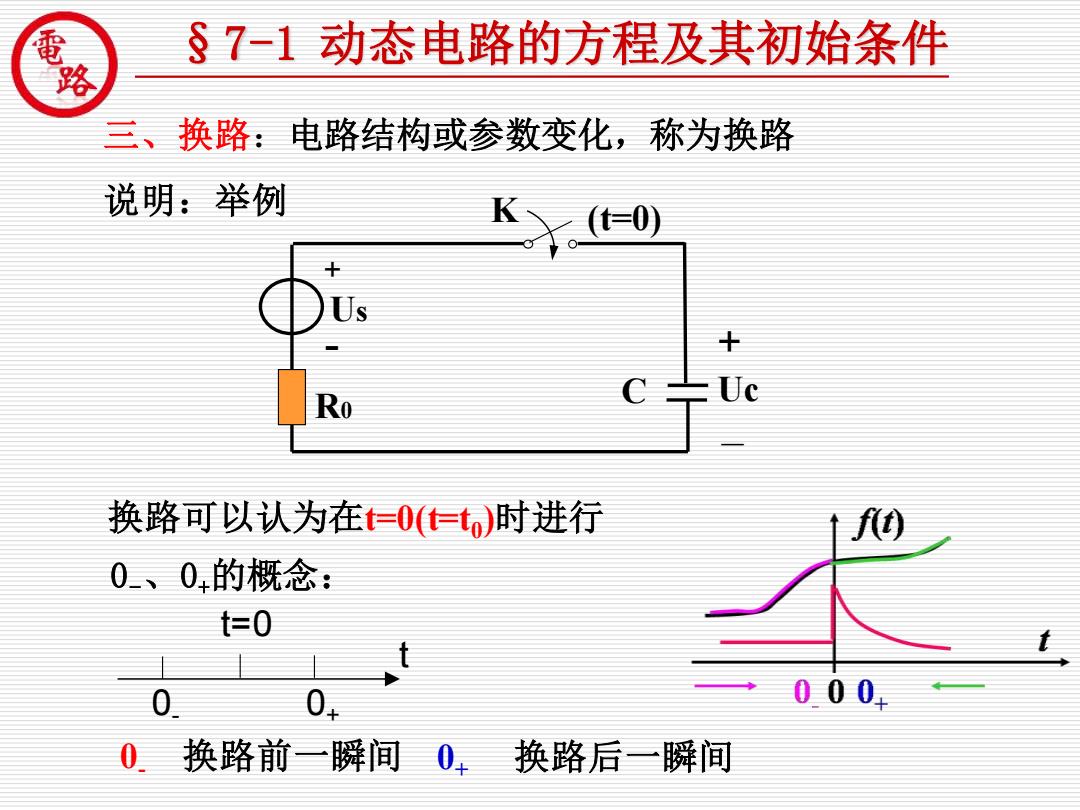
§7-1动态电路的方程及其初始条件 三、换路:电路结构或参数变化,称为换路 说明:举例 (t=0) Ro 换路可以认为在=O(仁)时进行 0、0,的概念: t=0 0 0 000号 0 换路前一瞬间0, 换路后一瞬间
现代制造装备工程技术开发中心 佛山科学技术学院 三、换路:电路结构或参数变化,称为换路 说明:举例 K (t=0) C + Uc - R0 Us 换路可以认为在t=0(t=t0 )时进行 0-、0+的概念: t=0 0- 0+ t §7-1 动态电路的方程及其初始条件 + - 0- 换路前一瞬间 0+ 换路后一瞬间
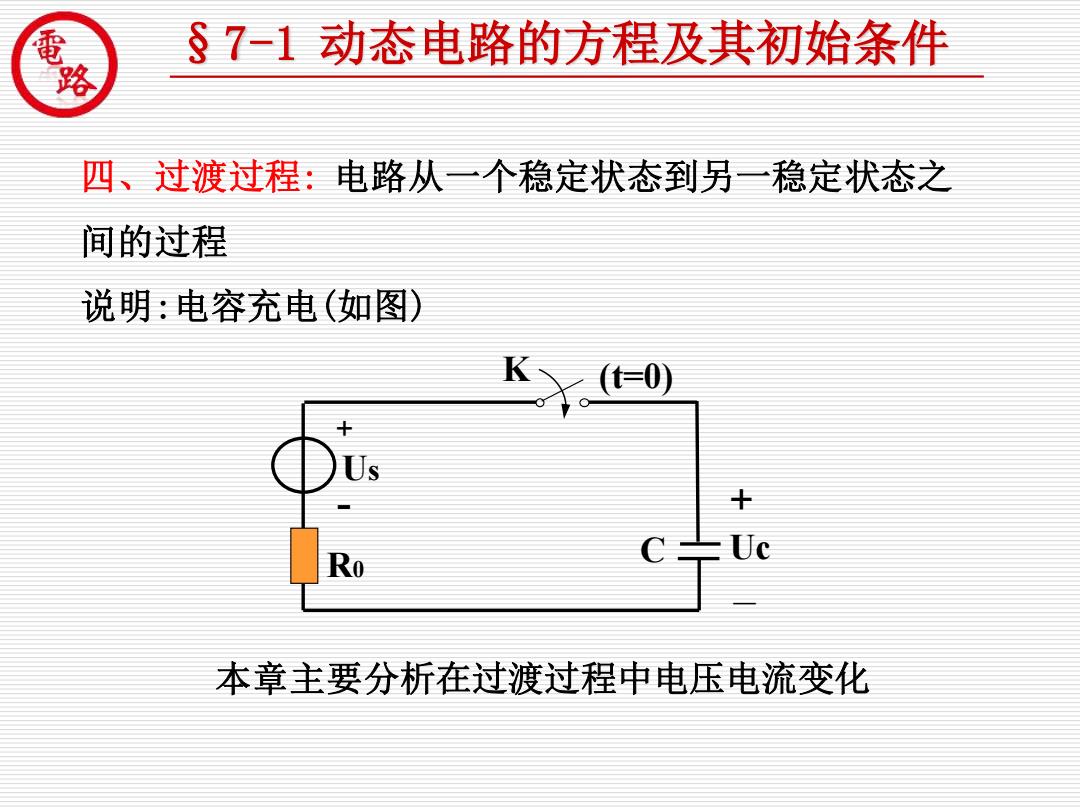
的 §7-1动态电路的方程及其初始条件 四、过渡过程:电路从一个稳定状态到另一稳定状态之 间的过程 说明:电容充电(如图) (=0) Ro 本章主要分析在过渡过程中电压电流变化
现代制造装备工程技术开发中心 佛山科学技术学院 四、过渡过程: 电路从一个稳定状态到另一稳定状态之 间的过程 说明:电容充电(如图) 本章主要分析在过渡过程中电压电流变化 K (t=0) C + Uc - R0 Us + - §7-1 动态电路的方程及其初始条件

的 第七章一阶电路和二阶电路 §7-1电路的初始状态 动态电路:微分方程 例:1C齐+Rc%4=04(0+)=?A0+)= 、初始条件 电路中电流电压在=O+时的值。 u0=4,,)+之 t=0士 t。=0利用 独立初始条件:u的初始值 说明:初始条件 非独立初始条件:除u外的其它i.u的初值
现代制造装备工程技术开发中心 佛山科学技术学院 第七章 一阶电路和二阶电路 2 2 0 c c c d u du LC RC u dt dt + + = uc (0 ) ? + = ' uc (0 ) ? + = §7-1 电路的初始状态 动态电路: 微分方程 例: 一、初始条件 电路中电流电压在t=0+ 时的值。 说明:初始条件 独立初始条件: c l u i c l u i 的初始值 非独立初始条件:除 外的其它i.u 的初值 0 0 1 ( ) ( ) t c c t u t u t idt c = + t 0 + = 0 t 0 − = 利用

裂 §71动态电路的方程及其初始条件 二、换路定理 1、线性C元件: 4e(0-)=ue(0月 说明:证明: a0=u6)h> 40)=4(0)+广d*40)=u09) 9.0)=9.(0)) '9=cu 若1=0时u.(0)=0则u.(0」=0 u.(0)=u.(0)成立条件时为有限值
现代制造装备工程技术开发中心 佛山科学技术学院 u (0+)= u (0-) c c = + ⎯ ⎯→ + = 0 0 0 1 ( ) ( ) t t t c c idt c u t u t − = 0 0 t 二、换路定理 1、线性C元件: 说明:证明: 0 0 1 (0 ) (0 ) (0 ) (0 ) i u u idt u u c c c c c + + − + − − = + ⎯⎯⎯⎯→ = 有限值 (0 ) (0 ) + − c = c q q q = cu = 0 (0 ) = 0 (0 ) = 0 − − + c c 若t 时u 则u uc (0 + ) = uc (0 − )成立条件时i为有限值 §7-1 动态电路的方程及其初始条件

鑫 §7-1动态电路的方程及其初始条件 2、线性L元件 0=0 说明:证明: =)d- t6=0 09=0)+ →0月=(0) (0)=(0月) ◆=Li 若1=0时(0)=0则,.(0)=0 (0)=,(0)成立条件时为有限值
现代制造装备工程技术开发中心 佛山科学技术学院 2、线性L元件 L L i (0+)= i (0-) = + ⎯ ⎯→ + = 0 0 0 1 ( ) ( ) t t t l l udt L i t i t − = 0 0 t (0 ) (0 ) 1 (0 ) (0 ) 0 0 + − + − + − = + ⎯⎯⎯⎯→ = L L u l l udt i i L i i 为有限值 (0 ) (0 ) + − l = l = Li = 0 (0 ) = 0 (0 ) = 0 − − + L L 若t 时i 则i i L (0 + ) = i L (0 − )成立条件时u为有限值 说明:证明: §7-1 动态电路的方程及其初始条件

经的 §71动态电路的方程及其初始条件 三:初始值计算步骤: 1)计算1-0时(0)u.(0) 2) 利用换路定律.(0)=u.(0))(0)=(0) L-用一电流为0)的电流源代潜 3)作0等效电路 C-用一电压为u.(0)的电压源代替 4)求解0电路。求出其它f0)
现代制造装备工程技术开发中心 佛山科学技术学院 0 (0 ) (0 ) − − − = L uc 计算t 时i (0 ) (0 ) + − 利用换路定律uc = uc (0 ) (0 ) + − L = L i i 三:初始值计算步骤: 1) L −用一电流为i L (0 + )的电流源代替 作 + 0 等效电路 C −用一电压为uc (0 + )的电压源代替 0 (0 ) + + 求解 电路。求出其它f 2) 3) 4) §7-1 动态电路的方程及其初始条件

经的 §71动态电路的方程及其初始条件 例1 +0 10k 40k uc 40k0 10V uc 求0) ()由0-电路求u(0)或i(0) 110k u(0)=8V 10V ic (2)由换路定律 0等效电路 uc(0,)=uc(0)=8V 3)由0,等效电路求i(0) i(0)=0主0) c(0,)= 10-8 =0.2mA 10
现代制造装备工程技术开发中心 佛山科学技术学院 (2) 由换路定律 uC (0+ ) = uC (0- )=8V 0.2mA 10 10 8 (0 ) = − i C + = (1) 由0-电路求 uC(0- ) 或 iL(0-) uC(0- )=8V (3) 由0+等效电路求 iC(0+ ) iC (0-- )=0 iC (0+ ) §7-1 动态电路的方程及其初始条件
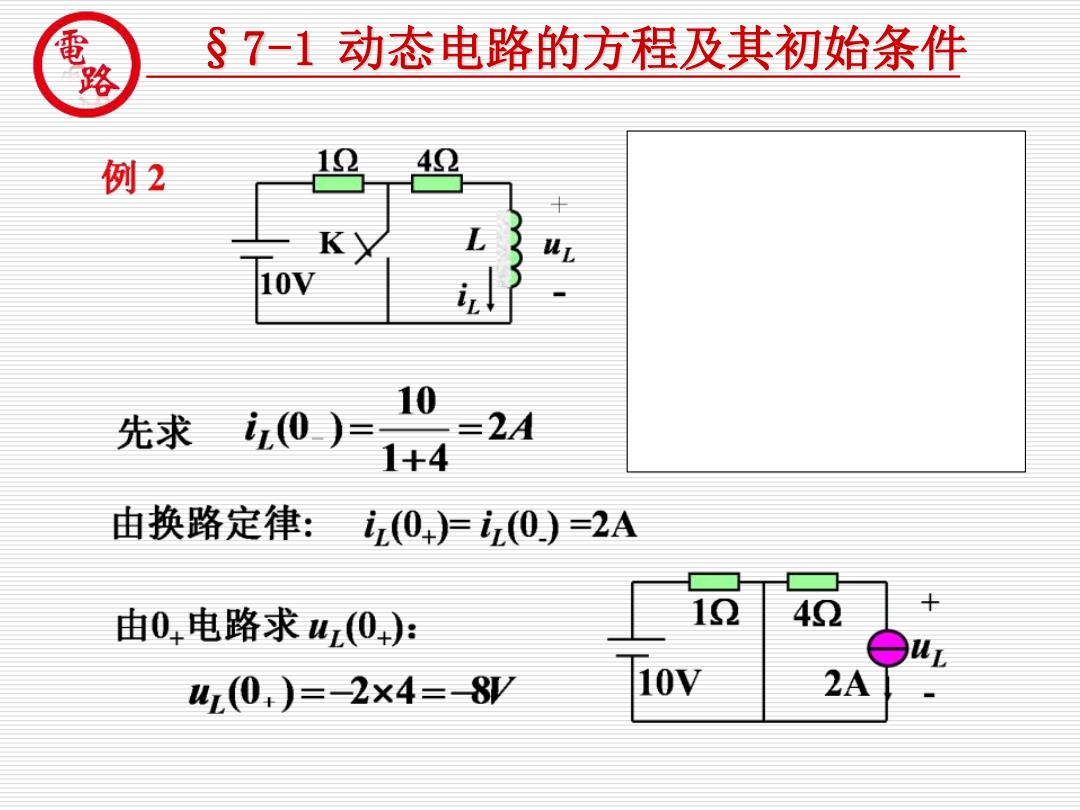
经的 §71动态电路的方程及其初始条件 例2 12 42 K 10V 14424 10 先求 0) 由换路定律:0)上(0)=2A 由0,电路求山(0): 12 42 u(0,)=2x4=8 10V 2A
现代制造装备工程技术开发中心 佛山科学技术学院 §7-1 动态电路的方程及其初始条件