佛山科学技术学院：《电路原理》课程教学资源（PPT课件讲稿）第九章 正弦稳态电路的分析

的 第九章正弦稳态电路的分析 本章内容：正弦电路、u计算 正弦电路P计算 §91阻抗和导纳 §9-2 电路的相量图 §9-3 正弦稳态电路的分析 §9-4正弦稳态电路的功率 §9-5复功率 §9-6最大功率传输

第九章 正弦稳态电路的分析 本章内容： 正弦电路 i、u 计算 正弦电路 P 计算 §9-1 阻抗和导纳 §9-2 电路的相量图 §9-3 正弦稳态电路的分析 §9-4 正弦稳态电路的功率 §9-5 复功率 §9-6 最大功率传输

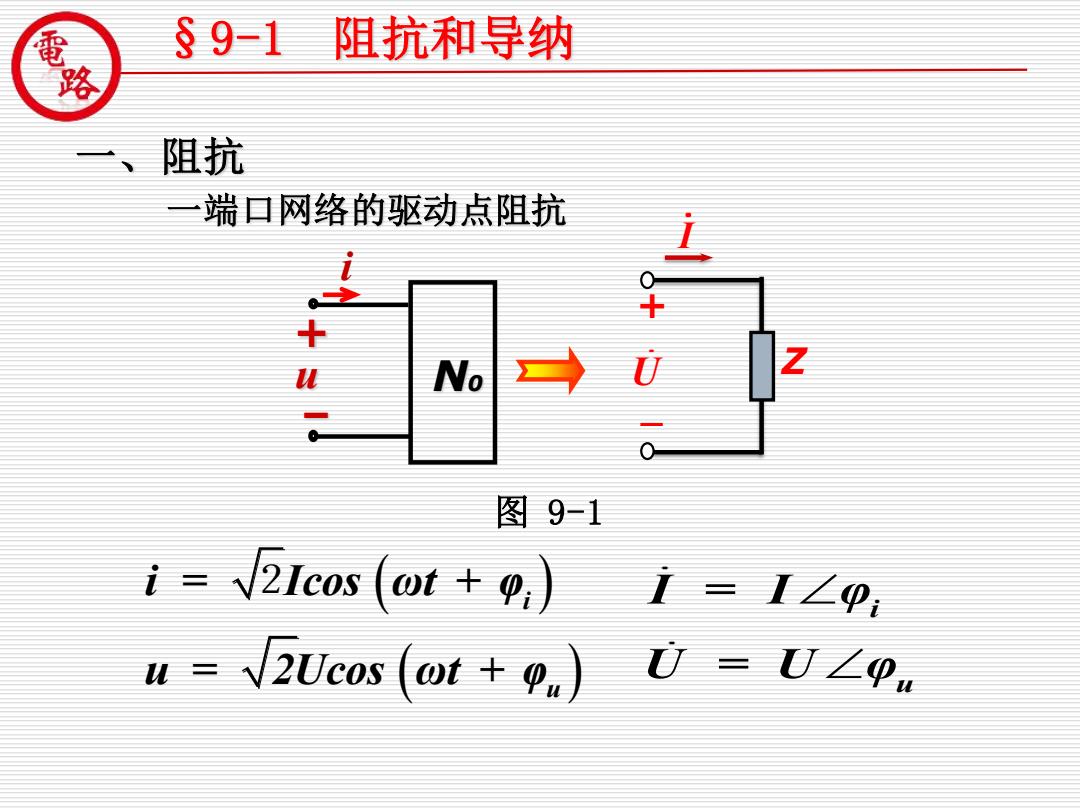
§91 阻抗和导纳 、阻抗 端口网络的驱动点阻抗 U No 图9-1 i-√2Icos(ot+p, =1Z9 u=√2 Veos (ot+9.) 0=0∠0

一、阻抗 一端口网络的驱动点阻抗 §9-1 阻抗和导纳 ( ) ( ) i u i = Icos ωt + φ u = 2Ucos ωt + φ ２ i u I = I φ U = U φ   图 9-1 u N0 i + – U I Z + -

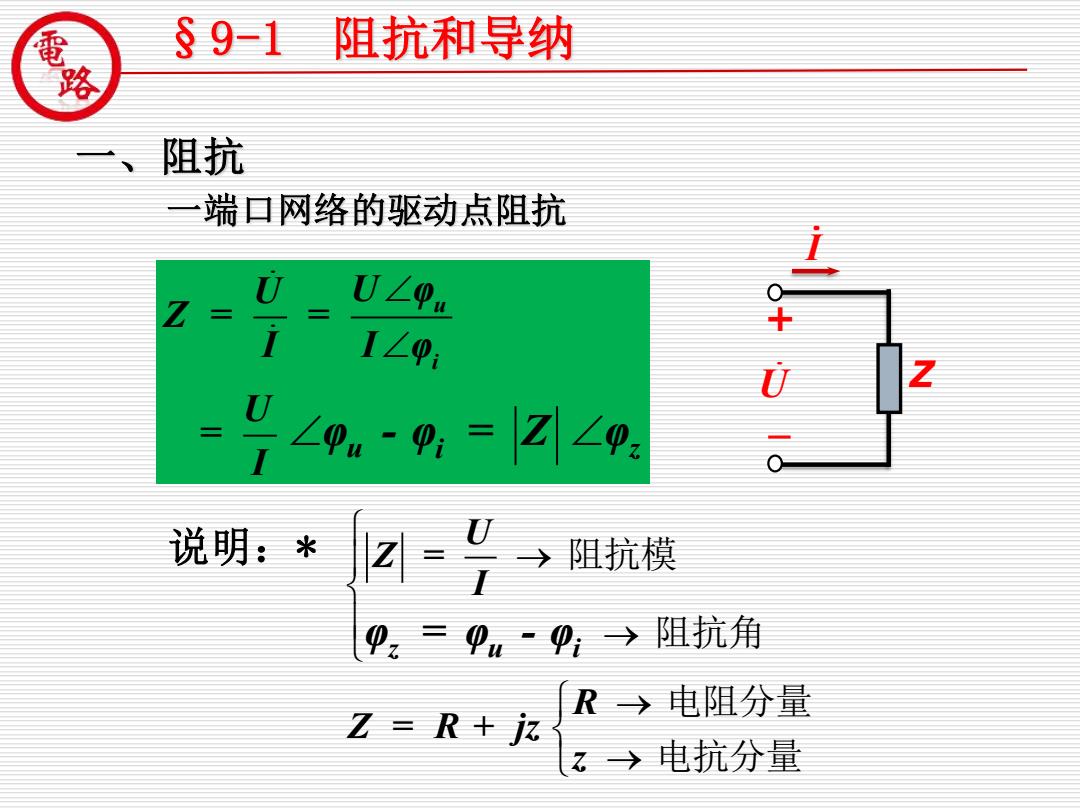
§91 阻抗和导纳 、阻抗 端口网络的驱动点阻抗 U U∠9u 1∠9： Z 0∠p。-9:=☑∠0： 说明：* →阻抗模 9z=9,-9;→阻抗角 R→电阻分量 Z=R+i 乙→电抗分量

一、阻抗 一端口网络的驱动点阻抗 §9-1 阻抗和导纳 U I Z + - u i u z i U U φ Z = = I I φ U = I φ - φ = Z φ     说明：* z u i U Z = I R Z = R + jz z φ = φ - φ 阻抗模 阻抗角 电阻分量 电抗分量   →    →  →   →

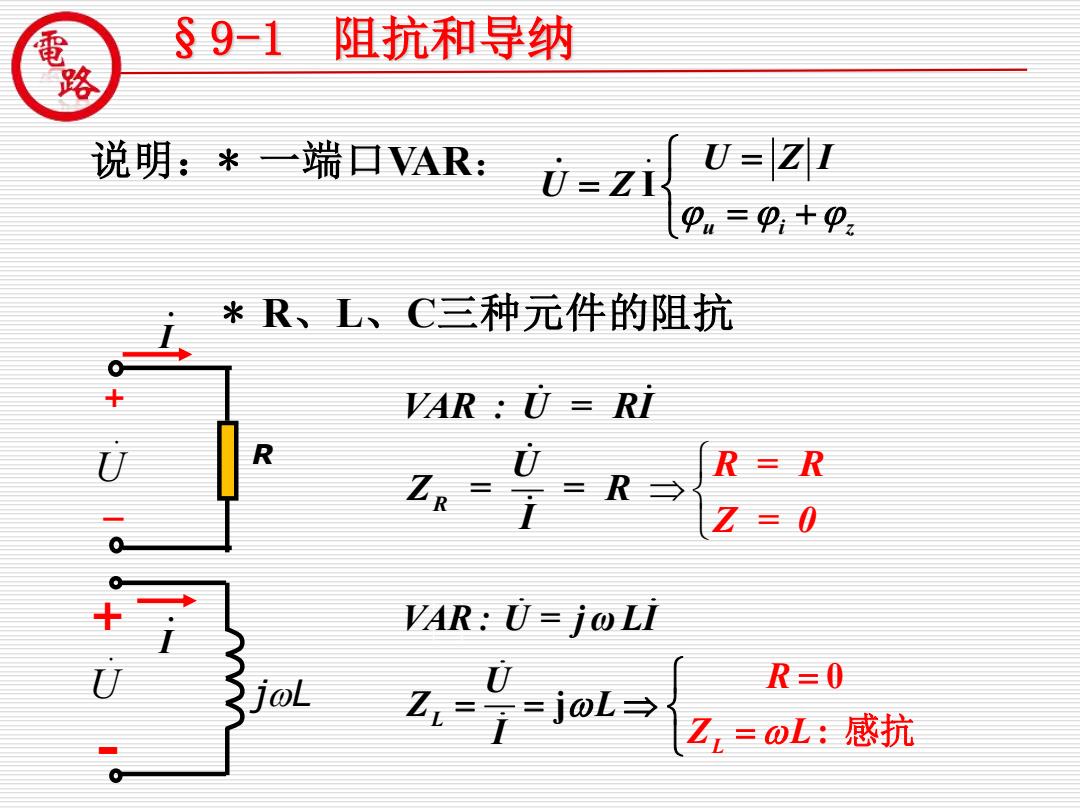
§91 阻抗和导纳 说明：*端回vAK:i=z 0=z 9.=9+9 米R、L、C三种元件的阻抗 0+: VAR:U=RI R Zn= R=R =R→ Z=0 VAR:U=jOLI joL Z-0-jol R=0 乙=oL:感抗

* R、L、C三种元件的阻抗 R VAR : U = RI U Z = = R R = R I Z = 0     + - . I R + _ . I . U . U jL . . I u i z U Z I U Z     = =  = +  j 0 : L L VAR : U = j ω LI U Z L I R Z L   = =  = =    感抗 §9-1 阻抗和导纳 说明：* 一端口VAR：

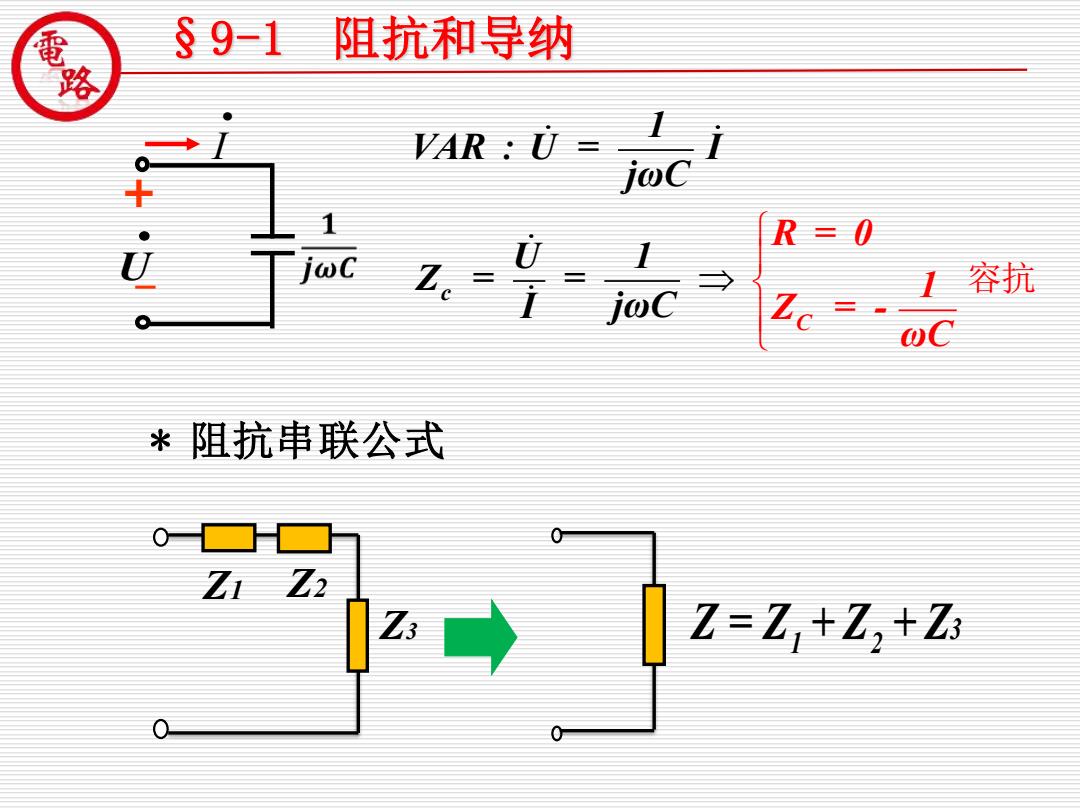
§91 阻抗和导纳 VAR:U= c R=0 1容抗 *阻抗串联公式 0口☐ Zi Za TEZ I

C c 1 VAR : U = I jωC U 1 Z = = R = 0 I jωC 1 Z = - ωC 容抗       * 阻抗串联公式 Z3 3 Z = Z + Z + Z 1 2 + _ • U • I §9-1 阻抗和导纳 Z1 Z2

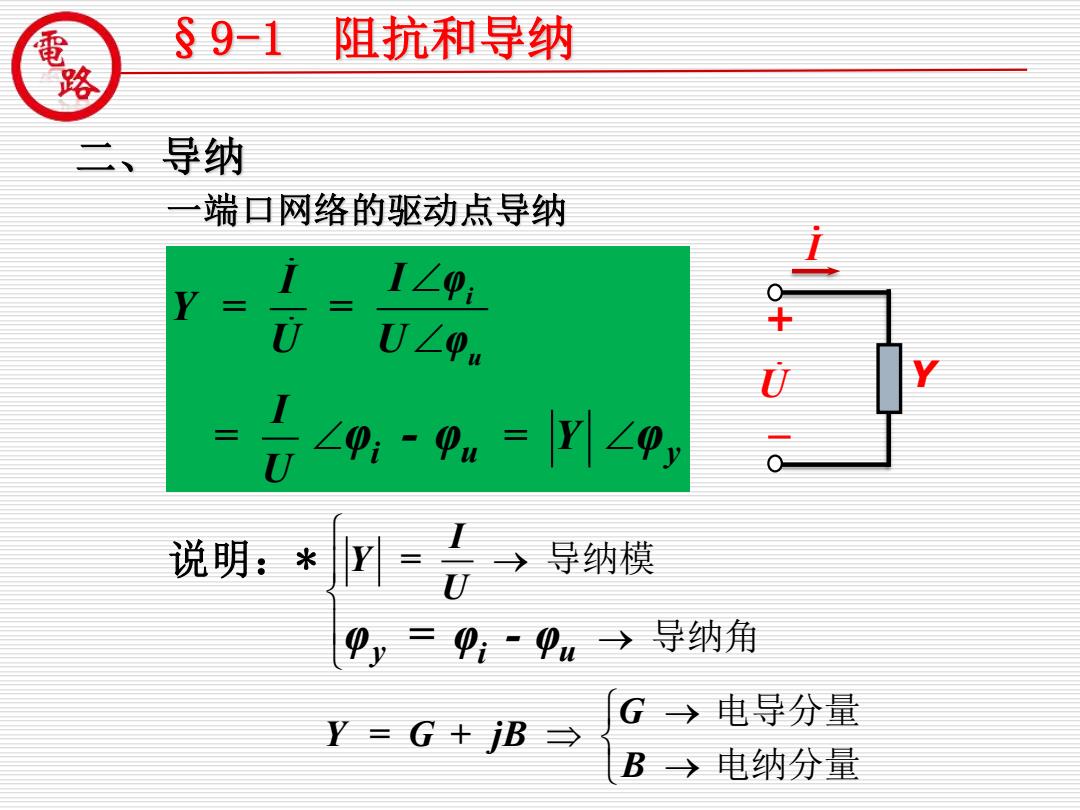
裂 §91 阻抗和导纳 二、导纳 一端▣网络的驱动点导纳 I∠p: U U∠0u 专%.=川9， 说明：*=号 导纳模 ,=4:94→导纳角 G>电导分量 Y=G+B→ B→电纳分量

二、导纳 一端口网络的驱动点导纳 §9-1 阻抗和导纳 U I Y + - i u i u y I I φ Y = = U U φ I = = Y U φ - φ φ     说明：* y u i I Y = U G Y = G + jB B φ = φ - φ 导纳模 导纳角 电导分量 电纳分量   →    →  →    →

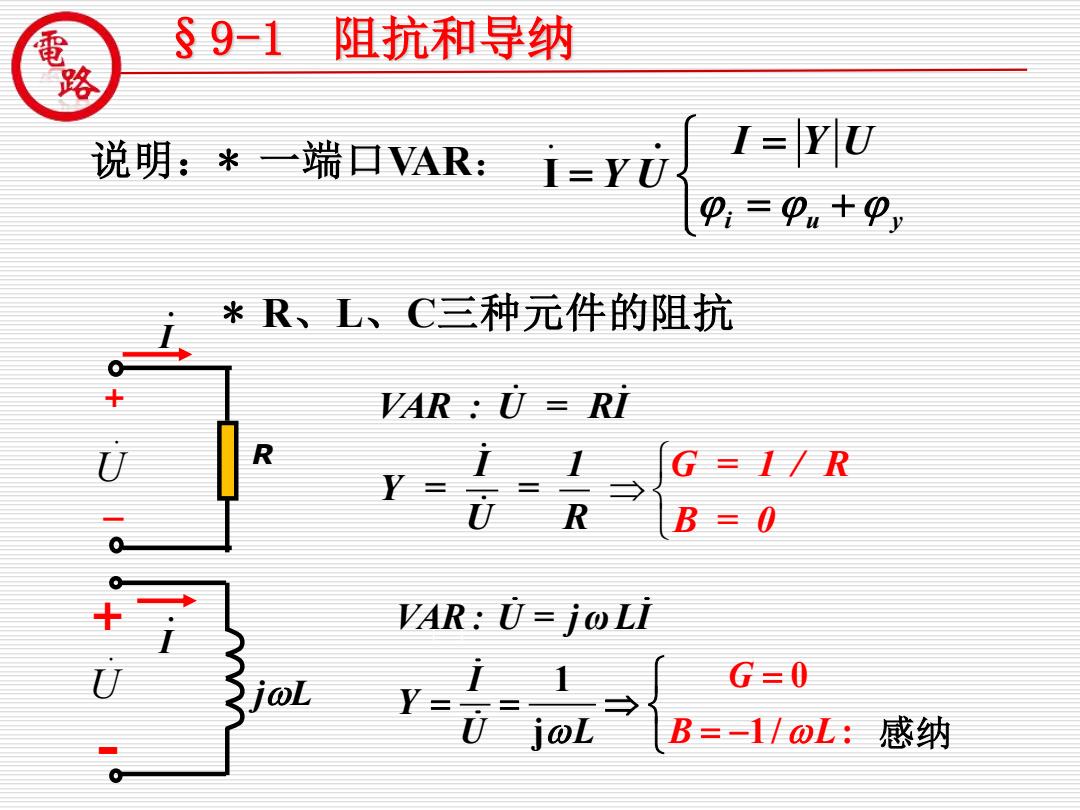
§91 阻抗和导纳 说明：*一端口Vk:ey元I回U 9=9+P 米R、L、C三种元件的阻抗 6+: VAR:U=Ri R G=1/R + Y= R B=0 AR:0=joL面 joL G=0 B=-1/oL:感纳

* R、L、C三种元件的阻抗 VAR : U = RI I 1 Y = = U G = 1 / R R B = 0     + - . I R + _ . I . U . U jL . . I i u y I Y U Y U     = =   = +  0 1 / : 1 j VAR : U = j ω LI I Y U G L B L  = =  = =   − §9-1 阻抗和导纳 说明：* 一端口VAR： 感纳

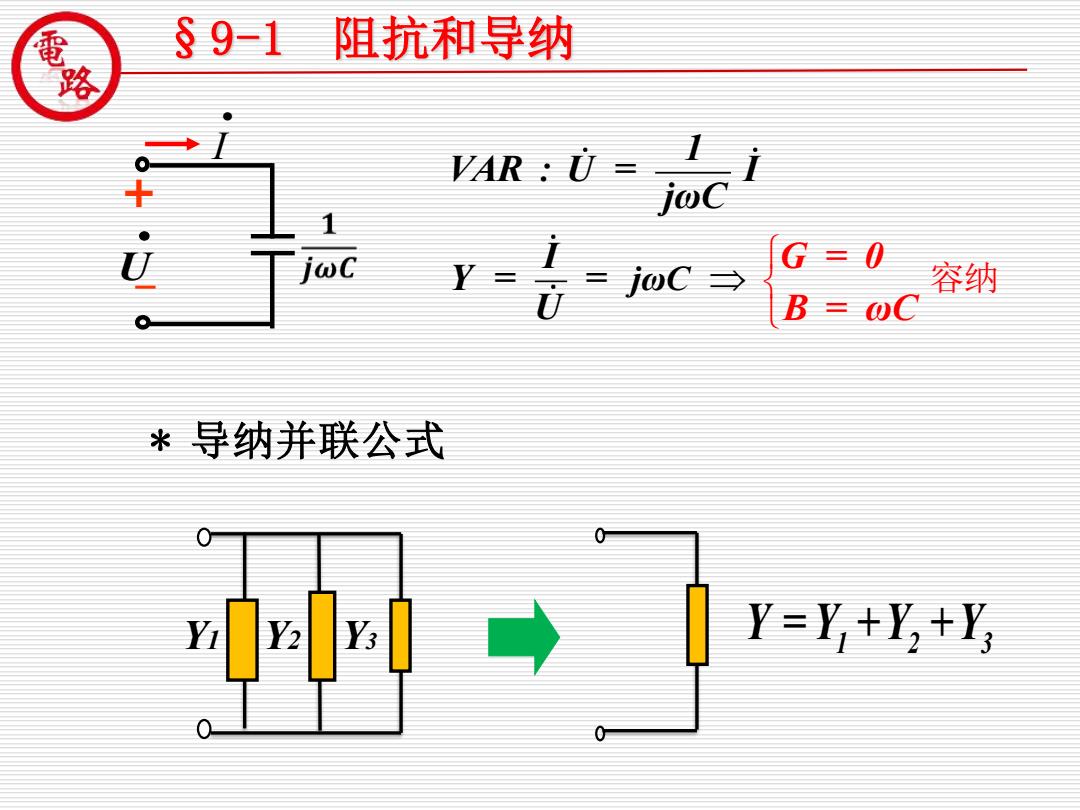
§91 阻抗和导纳 VAR:U= G=0 容纳 B ωC *导纳并联公式 3 Y=,+y,+ 0

jωC 1 VAR : U = I jωC I G = 0 B Y = = U = ωC 容纳     * 导纳并联公式 Y3 Y = Y +Y +Y 1 2 3 + _ • U • I §9-1 阻抗和导纳 Y1 Y2

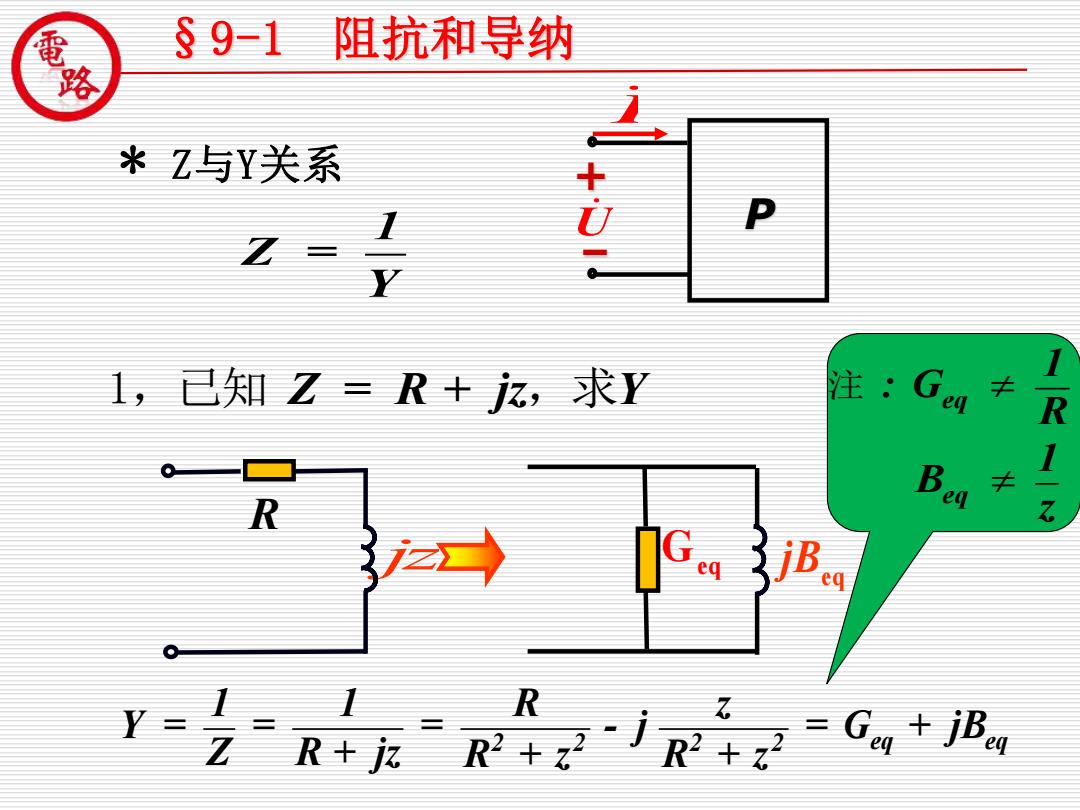
§9-1 阻抗和导纳 *Z与Y关系 Z三 + 1,已知Z=R+z,求Y 注 1 eq R B R q 1 R+RRzR2G,+地 R

* Z与Y关系 1 Z = Y P + – U  I  §9-1 阻抗和导纳 1，已知 Z = R + jz Y ，求 2 2 2 2 eq eq 1 1 R z Y = = = - j = G + jB Z R + jz R + z R + z jz eq Geq jB R eq eq 1 : G R 1 B z 注  

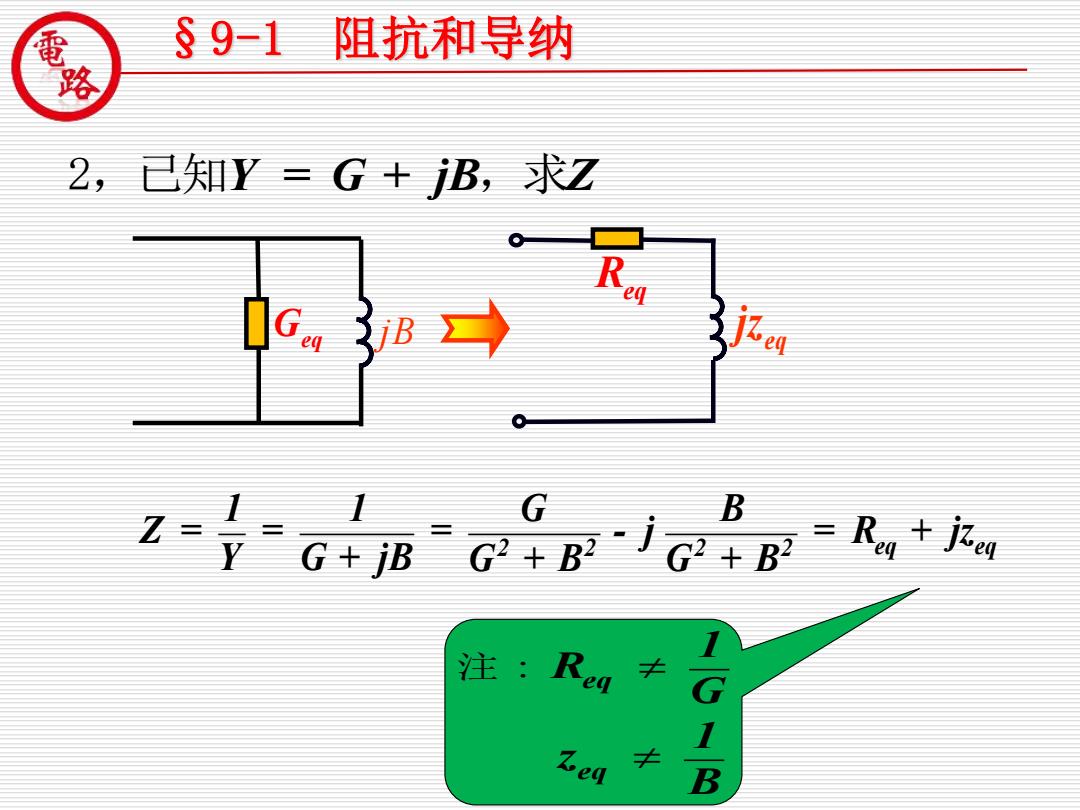
§9-1 阻抗和导纳 2,已知Y=G+B,求Z eq B G B G+iB GBBRo+o 注：Req 1-G 1e4 去 1 B

2，已知Y = G + jB Z ，求 eq eq 1 R G 1 z B 注 :   Geq jB eq jz R eq 2 2 2 2 eq eq 1 1 G B Z = = = - j = R + jz Y G + jB G + B G + B §9-1 阻抗和导纳