
怒的 第四章 利用电路原理分析电路 §41叠加定理 §4-2替代定理 §43戴维南定理 §特助根定理 84互易定理
现代制造装备工程技术开发中心 佛山科学技术学院 第四章 利用电路原理分析电路 §4-1 叠加定理 §4-2 替代定理 §4-3 戴维南定理 §4-4 特勒根定理 §4-5 互易定理

经的 第四章 电路定理 §4-1叠加定理 一、叠加定理:线性电路中任一支路的iu为多个独立电 源单独作用时在该支路上产生.u的叠加。 叠加定理证明见P82 范围:线性电路 受控源不参与叠加;某个独立源单独作用时,其它独立 电源置0,但受控源保留 电压源置0→短路 某独立电源单独作用其它电源置0 电流源置0→开路 叠加定理适用于求、u,但不能求功率
现代制造装备工程技术开发中心 佛山科学技术学院 §4-1 叠加定理 一、 叠加定理 :线性电路中任一支路的i.u 为多个独立电 源单独作用时在该支路上产生i.u 的叠加。 叠加定理证明 见P82 范围:线性电路 受控源不参与叠加;某个独立源单独作用时,其它独立 电源置0,但受控源保留 某独立电源单独作用其它电源置0 电压源置0→短路 电流源置0→开路 叠加定理适用于求 i、u,但不能求功率 第四章 电路定理

§41 叠加定理 举例 3 U, R动R,R E E E2 =,+ 44+4 i,3≠u+"u 代数和 共同作用时方向与单独作用时方向相同为+ (参考方向)共同作用时方向与单独作用时方向相反为
现代制造装备工程技术开发中心 佛山科学技术学院 = 举例 + ' " i u i 'u ' + i "u " 3 3 3 3 3 3 3 3 3 ' " u = u +u 3 3 3 i = i +i 代数和 (参考方向) 共同作用时方向与单独作用时方向相同为+ 共同作用时方向与单独作用时方向相反为- R1 E1 R2 E2 U3 R3 i3 + – R2 E1 U3 R3 ’ i3 ’ + – R1 R2 E2 U3 R3 ” i3 ” + – R1 §4-1 叠加定理

经的 §41叠加定理 二、举例说明叠加定理应用 1、不含受控源举例 2、含受控源举例 三、齐次定理 线性电路中当所有激励放大K倍,响应也放大K倍 说明:单激励时,响应与激励成正比 多激励时,必须全部激励均放大K培响应才放大K倍 齐次定理应用举例
现代制造装备工程技术开发中心 佛山科学技术学院 二、举例说明叠加定理应用 1、不含受控源 举例 2、含受控源 举例 三、齐次定理 线性电路中当所有激励放大K倍,响应也放大K倍 说明:单激励时,响应与激励成正比 多激励时,必须全部激励均放大K培响应才放大K倍 齐次定理应用举例 §4-1 叠加定理

效的 第四章【 电路定理 §4-2 替代定理 一、替代定理 线性电阻电路中,若第K支路电压Uk,电流,已知, 则此支路可用一个具有电压等于U的电压源or用一个电 流为.的独立电流源替代,替代前后电路中全部.u不变 说明 举例说明P89 被替代支路不能含受控源 证明(见教材)略 替代定理可推广到非线性电路 二、替代定理应用 证明戴维南定理
现代制造装备工程技术开发中心 佛山科学技术学院 §4-2 替代定理 一、替代定理 线性电阻电路中,若第 K支路电压 Uk,电流 ik已知, 则此支路可用一个具有电压等于Uk的电压源 or 用一个电 流为 ik的独立电流源替代,替代前后电路中全部 i.u 不变 说明 举例说明 P89 被替代支路不能含受控源 证明(见教材)略 替代定理 可推广到非线性电路 二、替代定理应用 证明戴维南定理 第四章 电路定理
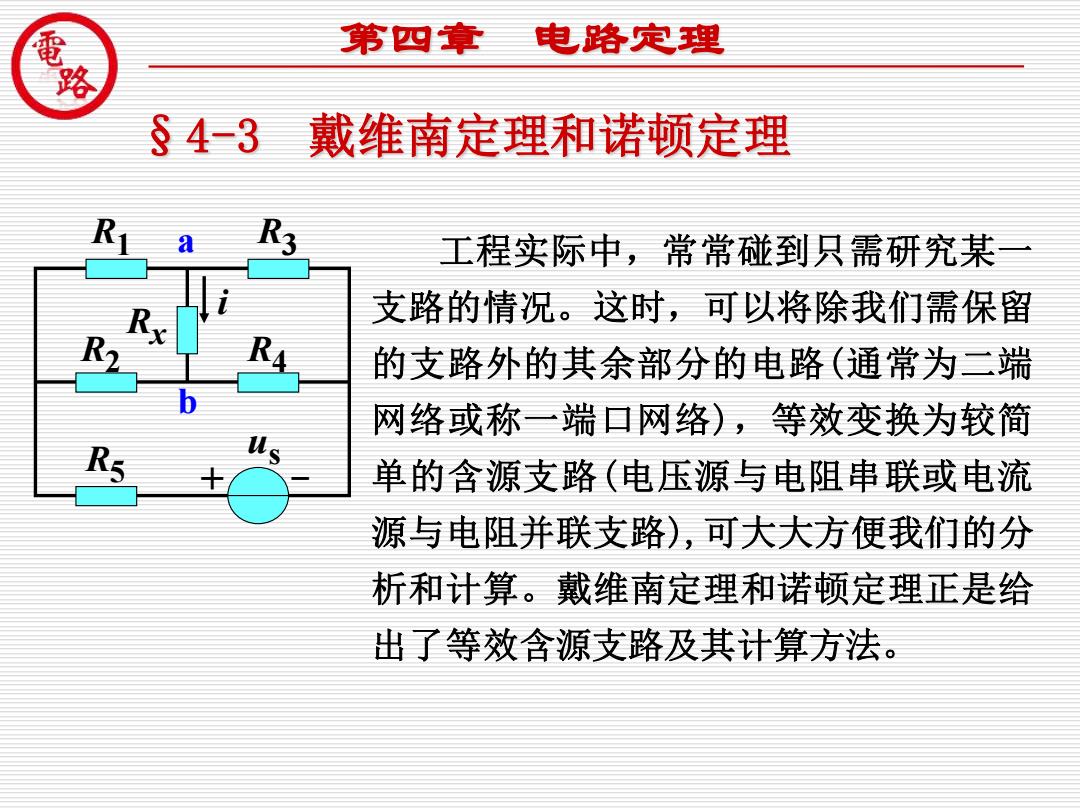
第四拿 电路定理 §4-3 戴维南定理和诺顿定理 R R3 工程实际中,常常碰到只需研究某 支路的情况。这时,可以将除我们需保留 的支路外的其余部分的电路(通常为二端 网络或称一端口网络),等效变换为较简 单的含源支路(电压源与电阻串联或电流 源与电阻并联支路),可大大方便我们的分 析和计算。戴维南定理和诺顿定理正是给 出了等效含源支路及其计算方法
现代制造装备工程技术开发中心 佛山科学技术学院 §4-3 戴维南定理和诺顿定理 第四章 电路定理 工程实际中,常常碰到只需研究某一 支路的情况。这时,可以将除我们需保留 的支路外的其余部分的电路(通常为二端 网络或称一端口网络),等效变换为较简 单的含源支路(电压源与电阻串联或电流 源与电阻并联支路),可大大方便我们的分 析和计算。戴维南定理和诺顿定理正是给 出了等效含源支路及其计算方法。 R1 R3 R5 R2 R4 i Rx a b + – us
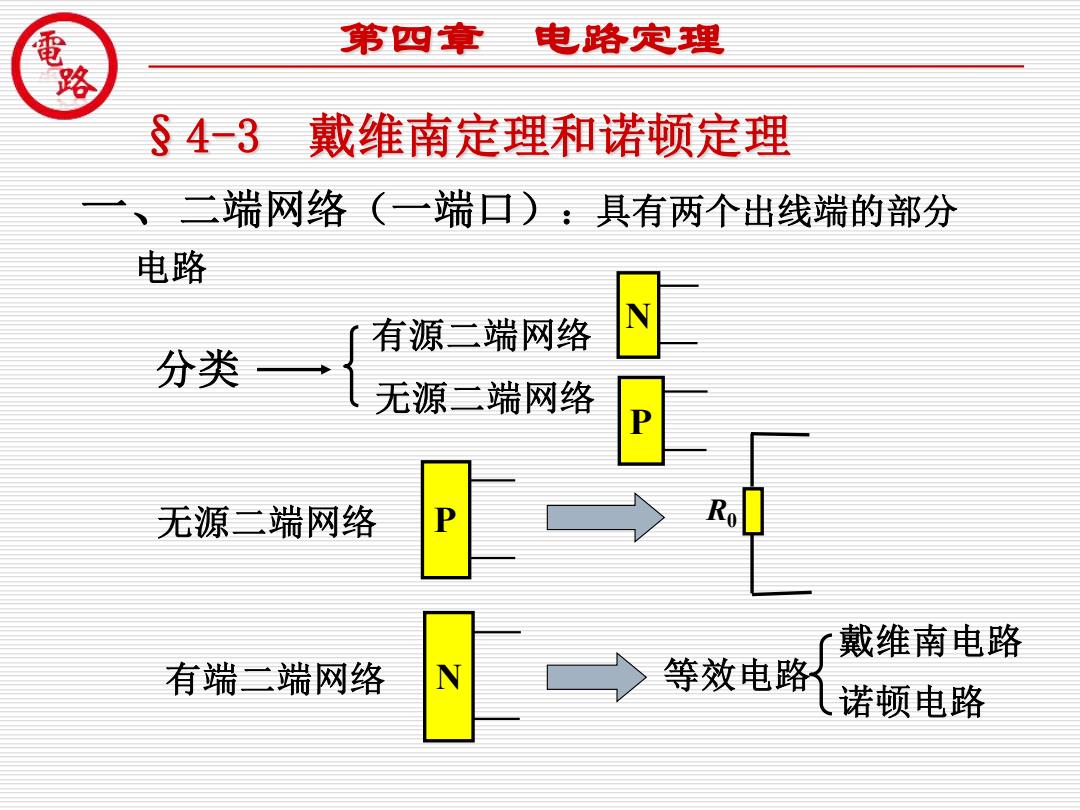
第四拿 电路定理 §4-3戴维南定理和诺顿定理 、二端网络(一端口):具有两个出线端的部分 电路 有源二端网络 N 分类 无源二端网络 P 无源二端网络 P Ro 戴维南电路 有端二端网络 等效电路 诺顿电路
现代制造装备工程技术开发中心 佛山科学技术学院 一、二端网络(一端口):具有两个出线端的部分 电路 N 分类 有源二端网络 无源二端网络 无源二端网络 P R0 有端二端网络 N 等效电路 戴维南电路 诺顿电路 P 第四章 电路定理 §4-3 戴维南定理和诺顿定理
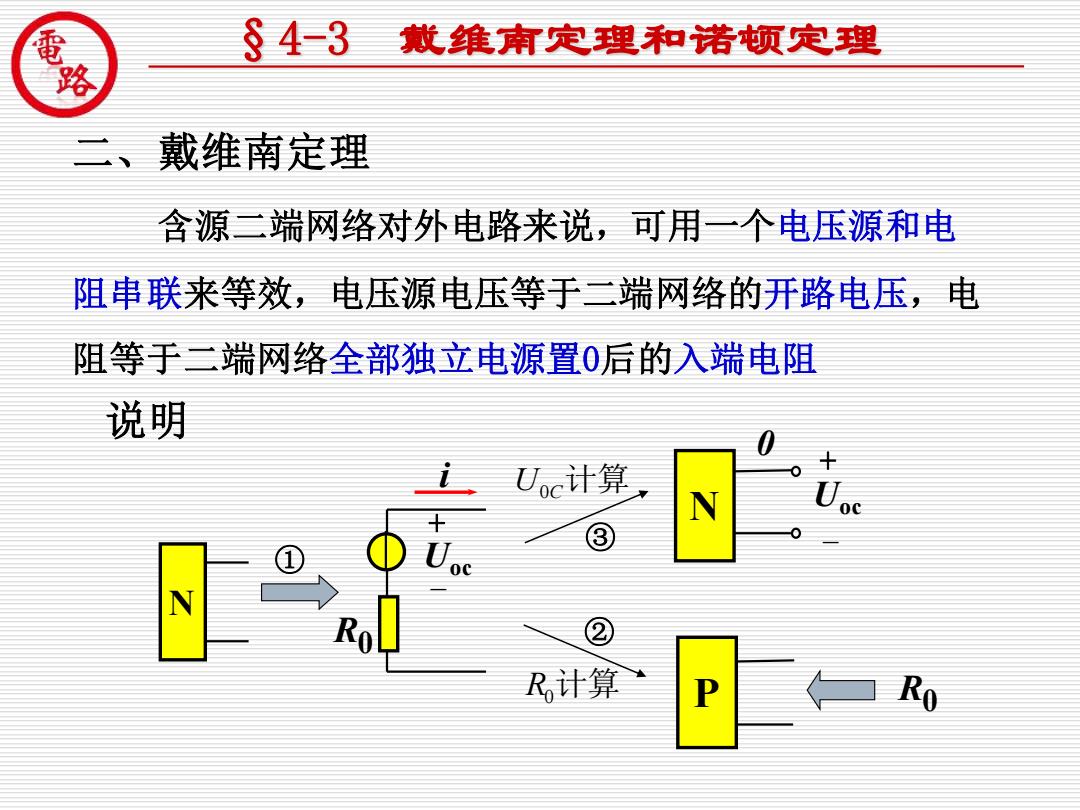
效 §43 戴维痢定理和诺顿定理 二、戴维南定理 含源二端网络对外电路来说,可用一个电压源和电 阻串联来等效,电压源电压等于二端网络的开路电压,电 阻等于二端网络全部独立电源置0后的入端电阻 说明 Uc计算 N ③ 00 N ② R计算 Ro
现代制造装备工程技术开发中心 佛山科学技术学院 二、戴维南定理 含源二端网络对外电路来说,可用一个电压源和电 阻串联来等效,电压源电压等于二端网络的开路电压,电 阻等于二端网络全部独立电源置0后的入端电阻 说明 N i R0 + Uoc - N 0 + Uoc - P R0 U0C计算 R0计算 ① ③ ② §4-3 戴维南定理和诺顿定理

经的 §4-3 戴维痢定理和诺顿定理 戴维南定理证明略P92(叠加定理+替代定理) 电压源开路 独立电源置0 电流源短路 开路电压,短路电流 十 N N
现代制造装备工程技术开发中心 佛山科学技术学院 戴维南定理证明 略 P92(叠加定理+替代定理) 独立电源置0 电压源开路 电流源短路 开路电压,短路电流 N sc N I + - Uoc §4-3 戴维南定理和诺顿定理

的 §43 戴维定理和诺顿定理 利用戴维南定理分析思路 N oc U R U R+Ro Uoc R+Ro 0 N Uc计算 无受控源:电阻本征公式 其中 R计算 P N R,= 有受控源 N R, Uoc
现代制造装备工程技术开发中心 佛山科学技术学院 利用戴维南定理分析思路 N + – U I RL R0 + - UOC RL – + U L OC L 0 R U = U R + R OC L 0 U I = R + R U0C计算 R0计算 其中 N + - Uoc P R0 无受控源:电阻本征公式 有受控源 N SC I N + – U I 0 U R = I OC 0 SC U R = I §4-3 戴维南定理和诺顿定理