
成都大学 CHENGDU UNIVERSITY 2018自动化专业 课程教学大纲 信息科学与工程学院 二0一八年七月
2018 自动化专业 课程教学大纲 信息科学与工程学院 二 O 一八年七月

目录 2018自动化专业课程教学大纲 (一)理论课程 1.《高等数学A+(1)》课程教学大纲 2.《高等数学A+(2)》课程教学大纲.9 3.《大学物理A1》课程教学大纲. .17 4.《线性代数A》课程教学大纲. .25 5.《复变函数与积分变换》课程教学大纲 .32 6.《概率论与数理统计C》课程教学大纲 39 7.《电路原理A》课程教学大纲.… …46 8.《模拟电子电路》课程教学大纲 .54 9.《数字电子电路》课程教学大纲. 64 10.《电子技术基础实验》课程教学大纲. .71 1L.《微机原理及接口技术》课程教学大纲. 77 12.《自动控制原理A》课程教学大纲 85 13.《自控原理实验》课程教学大纲.92 14.《电工电子实习》课程教学大纲.98 15.《微机原理及接口技术课程设计》教学大纲..104 16.《电机原理与拖动基础》课程教学大纲.110 17.《电气测量技术与传感器》课程教学大纲 .119 18.《电力电子技术》课程教学大纲..128 19.《过程控制系统(校企)》课程教学大纲 …36 20.《运动控制系统(校企)》课程教学大纲 .143 21.《自动控制系统工程项目设计(企业)》课程设计教学大纲.148 22.《运动控制系统(校企)》课程教学大纲」 ....152 23.《现场总线技术》课程教学大纲 157 24.《电气制图及CAD》课程教学大纲 ..163 25.《单片机应用及系统设计》课程教学大纲」 172 26.《单片机系统设计综合项目实践》教学大纲 183 27.《电气控制与PLC》课程教学大纲.… 189 28.《计算机控制技术》课程教学大纲 .202 29.《计算机控制技术课程设计》课程教学大纲 209 30.《电气控制技术与PLC》课程设计教学大纲. 218
目 录 2018 自动化专业课程教学大纲 (一)理论课程 1.《高等数学 A+(1)》课程教学大纲.................................................................. 1 2.《高等数学 A+(2)》课程教学大纲.................................................................. 9 3.《大学物理 A1》课程教学大纲..................................................................... 17 4.《线性代数 A》课程教学大纲....................................................................... 25 5.《复变函数与积分变换》课程教学大纲.......................................................32 6.《概率论与数理统计 C》课程教学大纲....................................................... 39 7.《电路原理 A》课程教学大纲....................................................................... 46 8.《模拟电子电路》课程教学大纲...................................................................54 9.《数字电子电路》课程教学大纲...................................................................64 10.《电子技术基础实验》课程教学大纲.........................................................71 11.《微机原理及接口技术》课程教学大纲..................................................... 77 12.《自动控制原理 A》课程教学大纲............................................................. 85 13.《自控原理实验》课程教学大纲.................................................................92 14.《电工电子实习》课程教学大纲.................................................................98 15.《微机原理及接口技术课程设计》教学大纲...........................................104 16.《电机原理与拖动基础》课程教学大纲................................................... 110 17.《电气测量技术与传感器》课程教学大纲............................................... 119 18.《电力电子技术》课程教学大纲...............................................................128 19.《过程控制系统(校企)》课程教学大纲.................................................136 20.《运动控制系统(校企)》课程教学大纲.................................................143 21.《自动控制系统工程项目设计(企业)》课程设计教学大纲.................148 22.《运动控制系统(校企)》课程教学大纲.................................................152 23.《现场总线技术》课程教学大纲...............................................................157 24.《电气制图及 CAD》课程教学大纲..........................................................163 25.《单片机应用及系统设计》课程教学大纲...............................................172 26.《单片机系统设计综合项目实践》教学大纲...........................................183 27.《电气控制与 PLC》课程教学大纲...........................................................189 28.《计算机控制技术》课程教学大纲...........................................................202 29.《计算机控制技术课程设计》课程教学大纲...........................................209 30.《电气控制技术与 PLC》课程设计教学大纲...........................................218

31.《现代控制理论》课程教学大纲 .225 32.《自动控制导论》课程教学大纲 .232 (二)实验课程 33.《大学物理A1》实验教学大纲. 235 34.《微机原理及接口技术》实验教学大纲 240 35.《电气测量技术与传感器》实验教学大纲248 36.《电路原理A》实验教学大纲 256 37.《电力电子技术》实验教学大纲. 261 38.《过程控制系统(校企)》实验教学大纲 271 39.《运动控制系统》实验教学大纲..278 40.《计算机控制技术》实验教学大纲. 285 41.《电气控制与PLC》实验教学大纲. .292 (三)实践课程 42.认知实习课程教学大纲 .308 43.毕业实习课程教学大纲. .313 44.毕业设计(论文)课程教学大纲319
31.《现代控制理论》课程教学大纲...............................................................225 32.《自动控制导论》课程教学大纲...............................................................232 (二)实验课程 33.《大学物理 A1》实验教学大纲................................................................. 235 34.《微机原理及接口技术》实验教学大纲...................................................240 35.《电气测量技术与传感器》实验教学大纲...............................................248 36.《电路原理 A》实验教学大纲................................................................... 256 37.《电力电子技术》实验教学大纲...............................................................261 38.《过程控制系统(校企)》实验教学大纲.................................................271 39.《运动控制系统》实验教学大纲...............................................................278 40.《计算机控制技术》实验教学大纲...........................................................285 41.《电气控制与 PLC》实验教学大纲...........................................................292 (三)实践课程 42.认知实习课程教学大纲...............................................................................308 43.毕业实习课程教学大纲...............................................................................313 44.毕业设计(论文)课程教学大纲...............................................................319

《高等数学A+(1)》课程教学大纲 一、课程概况 课程代码:04430011 课程名称:高等数学A+(I) 课程学分:4.5 课程学时:72(理论学时:72;实验(实践)学时:0) 课程性质:学科教育课程(必修) 开课部门:信息科学与工程学院 建议修读学期:1 建议先修课程:初等数学 适用专业(方向):理工科类本科生 二、课程地位、作用与任务 高等数学是现代高等教育的一门重要的学科知识,既是现代科学体系的基石,也是学习 更高理化等复杂学科知识的基础学科。本课程是理工科各专业人才培养计划中必不可少的基 础理论课程,为学习后继课程奠定必要的数学基础,也是硕士研究生入学考试的必考课程之 一。 通过本课程的学习,使学生理解微积分中极限、导数、积分等基本概念;掌握基本的运 算技巧;具有比较熟练的数学运算能力、抽象思维能力、逻辑推理能力、空间想象能力和 自学能力,特别是综合运用、分析解决实际问题的能力;训练学生在数学推理上的严密性, 使学生具有一定的数学修养和对实际问题具有抽象、归纳和推广的能力,能用数学语言描述 各种概念和现象,能理解其它学科中所用的数学理论和方法;培养学生学习数学的兴趣,帮 助学生养成自学的能力。 三、课程目标 (一)教学目标 高等数学A+(1)课程具体要求达到的特定教学目标包括: 1教学目标1.使学生掌握一元函数微积分学(极限、导数、不定积分、定积分、反常积分 等)、常微分方程等方面的基本概念、基本理论和基本运算技能。为学习后继课程及进一步 获取其它学科的知识莫定必要的数学基础。(指标点11) 2.救学目标2.培养学生具有比较熟练的数学运算能力、抽象思维能力、逻辑推理能力、空 间想象能力和自学能力,特别是综合运用、分析解决实际问题的能力,能用所学知识解决其 他领域中的一些问题。(指标点1.2)
1 《高等数学 A+(1)》课程教学大纲 一、课程概况 课程代码:04430011 课程名称:高等数学 A+(1) 课程学分:4.5 课程学时:72(理论学时:72;实验(实践)学时:0) 课程性质:学科教育课程(必修) 开课部门:信息科学与工程学院 建议修读学期:1 建议先修课程:初等数学 适用专业(方向):理工科类本科生 二、课程地位、作用与任务 高等数学是现代高等教育的一门重要的学科知识,既是现代科学体系的基石,也是学习 更高理化等复杂学科知识的基础学科。本课程是理工科各专业人才培养计划中必不可少的基 础理论课程,为学习后继课程奠定必要的数学基础,也是硕士研究生入学考试的必考课程之 一。 通过本课程的学习,使学生理解微积分中极限、导数、积分等基本概念;掌握基本的运 算技巧;具有比较熟练的数学运算能力、抽象思维能力、 逻辑推理能力、空间想象能力和 自学能力,特别是综合运用、分析解决实际问题的能力;训练学生在数学推理上的严密性, 使学生具有一定的数学修养和对实际问题具有抽象、归纳和推广的能力,能用数学语言描述 各种概念和现象,能理解其它学科中所用的数学理论和方法;培养学生学习数学的兴趣,帮 助学生养成自学的能力。 三、课程目标 (一)教学目标 高等数学 A+(1)课程具体要求达到的特定教学目标包括: 1.教学目标 1. 使学生掌握一元函数微积分学(极限、导数、不定积分、定积分、反常积分 等)、常微分方程等方面的基本概念、基本理论和基本运算技能。为学习后继课程及进一步 获取其它学科的知识奠定必要的数学基础。(指标点 1.1) 2.教学目标 2. 培养学生具有比较熟练的数学运算能力、抽象思维能力、 逻辑推理能力、空 间想象能力和自学能力,特别是综合运用、分析解决实际问题的能力,能用所学知识解决其 他领域中的一些问题。(指标点 1.2)

3教学目标3.培养学生具有一定的数学修养,能用数学语言描述各种概念和现象,能理解 其它学科中所用的数学理论和方法。(指标点1.4) 4.教学目标4.培养学生学习数学的兴趣,帮助学生养成自学的能力,具有不断学习和适应 发展的能力。(指标点2.1) (二)本课程支撑的半业要求 1.本课程支撑的毕业要求:毕业要求1、2、12。(毕业要求见2018版人才培养方案) 2.本课程支撑的指标点:指标点1.1、1.2、1.4、2.1。 (1)指标点1.1:能将数学、自然科学、工程基础和专业知识用到复杂工程问题的恰当表述 中。 (2)指标点1.2:能针对一个系统或者过程建立合适的数学模型,并利用恰当的方式求解。 (3)指标点1.4:能用专业知识,通过模型比较和综合,优选工程问题的解决方案,完成系 统的设计和计算。 (4)指标点2.1:能识别和判断复杂工程问题的关键环节和参数。 (三)课程教学目标与半业要求对应表 《高等数学A+1)》课程教学目标与半业要求的对应表 课程名称:高等数学A+(1)》 任课教师:韩天勇、陈丹等 课程性质:学科教育课程(必修) 课程学分:4.5 课程支撑的半业要求 课程目标、达成途径、评价依据 毕业要求1: 教学目标:培养学生利用高等数学基础理论知识解决工 指标点1.1:能将数学、自然科学、 程问题的能力。 工程基础和专业知识用到复杂工 达成途径:通过掌握一元函数微积分学、常微分方程理 程问题的恰当表述中 论内容,训练学生综合运用高等数学知识,解决工程问 题。 评价依据:课堂笔记、提问和作业、课外作业和考试。 半业要求1: 教学目标:培养学生综合应用高等数学理论知识解决工 指标点1.2:能针对一个系统或者 程问题的能力。 过程建立合适的数学模型,并利 达成途径:运用高等数学的基本理论和基本观点,通过 用恰当的方式求解。 观察、空间想象、逻辑推理分析、综合运算演绎、归纳、 类比联想、文献研究等方法发现问题、提出问题,抓住 主要矛盾,进行合理的简化,建立相应的数学模型。 评价依据:提问和作业、课外作业和考试。 半业要求1: 教学目标:培养学生学习数学的兴趣,帮助学生养成自 指标点1.4:能用专业知识,通过 学的能力,并具有不断学习和适应发展的能力。 模型比较和综合,优选工程问题 达成途径:通过本课程的学习,运用多种教学方式和多 的解决方案,完成系统的设计和 媒体工具,培养学生学习数学的兴趣,具有一定的数学 计算 修养;养成自学的能力,不断学习,适应发展。 评价依据:提问和作业、课外作业和考试。 毕业要求2: 教学目标:培养抽象知识的应用能力,能分析工程问题 指标点2.1:能识别和判断复杂 的数学模型的关键环节和参数,帮助学生养成分析问题 工程问题的关键环节和参数 的能力。 2
2 3.教学目标 3. 培养学生具有一定的数学修养,能用数学语言描述各种概念和现象,能理解 其它学科中所用的数学理论和方法。(指标点 1.4) 4.教学目标 4. 培养学生学习数学的兴趣,帮助学生养成自学的能力,具有不断学习和适应 发展的能力。(指标点 2.1) (二)本课程支撑的毕业要求 1. 本课程支撑的毕业要求:毕业要求 1、2、12。(毕业要求见 2018 版人才培养方案) 2. 本课程支撑的指标点:指标点 1.1、1.2、1.4、2.1。 (1)指标点 1.1:能将数学、自然科学、工程基础和专业知识用到复杂工程问题的恰当表述 中。 (2)指标点 1.2:能针对一个系统或者过程建立合适的数学模型,并利用恰当的方式求解。 (3)指标点 1.4:能用专业知识,通过模型比较和综合,优选工程问题的解决方案,完成系 统的设计和计算。 (4)指标点 2.1:能识别和判断复杂工程问题的关键环节和参数。 (三)课程教学目标与毕业要求对应表 《高等数学 A+(1)》课程教学目标与毕业要求的对应表 课程名称:高等数学 A+(1) 任课教师:韩天勇、陈丹等 课程性质:学科教育课程(必修) 课程学分:4.5 课程支撑的毕业要求 课程目标、达成途径、评价依据 毕业要求 1: 指标点 1.1:能将数学、自然科学、 工程基础和专业知识用到复杂工 程问题的恰当表述中 教学目标:培养学生利用高等数学基础理论知识解决工 程问题的能力。 达成途径:通过掌握一元函数微积分学、常微分方程理 论内容,训练学生综合运用高等数学知识,解决工程问 题。 评价依据:课堂笔记、提问和作业、课外作业和考试。 毕业要求 1: 指标点 1.2:能针对一个系统或者 过程建立合适的数学模型,并利 用恰当的方式求解。 教学目标:培养学生综合应用高等数学理论知识解决工 程问题的能力。 达成途径:运用高等数学的基本理论和基本观点,通过 观察、空间想象、逻辑推理分析、综合运算演绎、归纳、 类比联想、文献研究等方法发现问题、提出问题,抓住 主要矛盾,进行合理的简化,建立相应的数学模型。 评价依据:提问和作业、课外作业和考试。 毕业要求 1: 指标点 1.4:能用专业知识,通过 模型比较和综合,优选工程问题 的解决方案,完成系统的设计和 计算 教学目标:培养学生学习数学的兴趣,帮助学生养成自 学的能力,并具有不断学习和适应发展的能力。 达成途径:通过本课程的学习,运用多种教学方式和多 媒体工具,培养学生学习数学的兴趣,具有一定的数学 修养;养成自学的能力,不断学习,适应发展。 评价依据:提问和作业、课外作业和考试。 毕业要求 2: 指标点 2.1:能识别和判断复杂 工程问题的关键环节和参数 教学目标:培养抽象知识的应用能力,能分析工程问题 的数学模型的关键环节和参数,帮助学生养成分析问题 的能力

达成途径:通过本课程的学习,运用多种数学基本思想、 方法,培养学生模型分析能力,并用数学语言和基本数 学方法进行描述,运用所学的数学理论和研究方法进行 分析、运算和研究,获得有效结论,促进学生不断学习, 适应专业发展。 评价依据:提问和作业、课外作业和考试。 四、课程目标对学习成果的支撑关系 学习成果 学习成果指标点 课程目标 11能将数学、自然科学、工程基础和 专业知识用到复杂工程问题的恰当表 课程目标1 1.工程知识:具备良好的工程知识, 述中; 能够将数学、自然科学、工程基础 1.2能针对一个系统或者过程建立合适 和专业知识用于解决自动化控制系 课程目标2 的数学模型,并利用恰当的方式求解: 统、自动化测试系统开发或集成中 1.4能用专业知识,通过模型比较和综 的复杂工程问题; 合,优选工程问题的解决方案,完成系 课程目标3 统的设计和计算; 2.问题分析:能够应用数学、自然 科学和工程科学的基本原理,识别、 2.1能识别和判断复杂工程问题的关键 表达、并通过文献研究分析自动化 课程目标4 控制系统的复杂工程问题,以获得 环节和参数; 有效结论: 五、教学内容与课程目标的关系 教学内容 作业要求 第一章函数、极限与连续 自学内容:函数的基本概念、相关性质、简 1.1函数 单函数关系式的建立。 1.2数列的极限 1.3函数的极限 课堂作业: 1.4无穷小与无穷大 1.函数相关性质(奇偶性、单调性、周期性 1.5极限的运算法则 和有界性)的应用 1.6极限的存在准则两个重要极限 2.函数极限的运算法则的应用 1.7无穷小的比较 3极限存在的两个准则的应用 1.8函数的连续与间断点 4.两个重要极限的应用 1.9初等函数的连续性 5利用等价无穷小求极限 1.10闭区间上连续函数的性质 6.函数的连续性的应用,特别是闭区间上连 知识点: 续函数的性质应用 1.了解函数的概念与表示方法、函数的奇偶 性、单调性、周期性和有界性。 课外作业: 2.反函数、复合函数、隐函数的概念,筒单 1.完成本章小结 函数关系式的建立。 2.函数极限的求解 3.了解基本初等函数的性质与图形。 3闭区间上连续函数的性质应用
3 达成途径:通过本课程的学习,运用多种数学基本思想、 方法,培养学生模型分析能力,并用数学语言和基本数 学方法进行描述,运用所学的数学理论和研究方法进行 分析、运算和研究,获得有效结论,促进学生不断学习, 适应专业发展。 评价依据:提问和作业、课外作业和考试。 四、课程目标对学习成果的支撑关系 学习成果 学习成果指标点 课程目标 1.工程知识:具备良好的工程知识, 能够将数学、自然科学、工程基础 和专业知识用于解决自动化控制系 统、自动化测试系统开发或集成中 的复杂工程问题; 1.1 能将数学、自然科学、工程基础和 专业知识用到复杂工程问题的恰当表 述中; 课程目标 1 1.2 能针对一个系统或者过程建立合适 的数学模型,并利用恰当的方式求解; 课程目标 2 1.4 能用专业知识,通过模型比较和综 合,优选工程问题的解决方案,完成系 统的设计和计算; 课程目标 3 2.问题分析:能够应用数学、自然 科学和工程科学的基本原理,识别、 表达、并通过文献研究分析自动化 控制系统的复杂工程问题,以获得 有效结论; 2.1 能识别和判断复杂工程问题的关键 环节和参数; 课程目标 4 五、教学内容与课程目标的关系 教学内容 作业要求 第一章 函数、极限与连续 1.1 函数 1.2 数列的极限 1.3 函数的极限 1.4 无穷小与无穷大 1.5 极限的运算法则 1.6 极限的存在准则 两个重要极限 1.7 无穷小的比较 1.8 函数的连续与间断点 1.9 初等函数的连续性 1.10 闭区间上连续函数的性质 知识点: 1. 了解函数的概念与表示方法、函数的奇偶 性、单调性、周期性和有界性。 2. 反函数、复合函数、隐函数的概念,简单 函数关系式的建立。 3. 了解基本初等函数的性质与图形。 自学内容:函数的基本概念、相关性质、简 单函数关系式的建立。 课堂作业: 1.函数相关性质(奇偶性、单调性、周期性 和有界性)的应用 2.函数极限的运算法则的应用 3.极限存在的两个准则的应用 4.两个重要极限的应用 5.利用等价无穷小求极限 6.函数的连续性的应用,特别是闭区间上连 续函数的性质应用 课外作业: 1.完成本章小结 2.函数极限的求解 3.闭区间上连续函数的性质应用

4.了解极限的概念与精确定义。 5.了解数列的性质 6.掌握分段函数极限的求解方法。 7.理解极限的四则运算法则。 8.了解复合函数的极限运算法则。 9.掌握极限存在的两个准则及利用其求极 限。 10.掌握两个重要极限及利用其求极限。 11.掌握无穷小、无穷大以及无穷小的阶的概 念,会用等价无穷小求极限。 12.理解函数的连续性和闭区间上连续函数 的性质,及性质的应用。 第二章导数与微分 自学内容:导数的概念 2.1导数的概念 2.2函数的求导法则 课堂作业: 2.3高阶导数 1.函数导数的求解 2.4隐函数及由参数方程所确定的函数导数 2.函数的可导与连续性之间的关系应用 2.5函数的微分 3.导数运算法则使用的练习 知识点: 1.理解导数和微分的概念 课外作业: 2.理解导数的几何意义 1.完成本章小结 3.函数的可导性与连续性之间的关系 2.函数导数与微分的求解 4.掌握导数的四则运算法则 5.掌握复合函数的求导法 6.基本初等函数的导数公式 7.微分的四则运算法则 8.理解微分形式不变性 9.理解高阶导数的概念 10.掌握初等函数一阶、二阶导数的求法 11.掌握求隐函数和参数式所确定的函数的 阶、二阶导数 12.了解求反函数的导数 第三章定理与导数的应用 自学内容:微分中值定理 3.1微分中值定理 3.2洛必达法则 课堂作业: 3.3泰勒公式 1.微分中值定理的应用 3.4函数的单调性与凹凸性 2.洛必达法则的应用 3.5函数的极值和最值 3函数图形的描绘、渐近线的求解 3.6函数图形的描绘 3.7*曲线的曲率 课外作业: 知识点: 1.完成本章小结 1.理解罗尔(Rolle)定理 2应用微分中值定理求解实际问题 2.理解拉格朗日(Lagrange)定理 3应用洛必达法则求导 3.了解柯西(Cauchy)定理 4求函数的单调性、凹凸性、极值和最值
4 4. 了解极限的概念与精确定义。 5. 了解数列的性质 6. 掌握分段函数极限的求解方法。 7. 理解极限的四则运算法则。 8. 了解复合函数的极限运算法则。 9. 掌握极限存在的两个准则及利用其求极 限。 10. 掌握两个重要极限及利用其求极限。 11. 掌握无穷小、无穷大以及无穷小的阶的概 念,会用等价无穷小求极限。 12. 理解函数的连续性和闭区间上连续函数 的性质,及性质的应用。 第二章 导数与微分 2.1 导数的概念 2.2 函数的求导法则 2.3 高阶导数 2.4 隐函数及由参数方程所确定的函数导数 2.5 函数的微分 知识点: 1. 理解导数和微分的概念 2. 理解导数的几何意义 3. 函数的可导性与连续性之间的关系 4. 掌握导数的四则运算法则 5. 掌握复合函数的求导法 6. 基本初等函数的导数公式 7. 微分的四则运算法则 8. 理解微分形式不变性 9. 理解高阶导数的概念 10. 掌握初等函数一阶、二阶导数的求法 11. 掌握求隐函数和参数式所确定的函数的一 阶、二阶导数 12. 了解求反函数的导数 自学内容:导数的概念 课堂作业: 1.函数导数的求解 2.函数的可导与连续性之间的关系应用 3.导数运算法则使用的练习 课外作业: 1.完成本章小结 2.函数导数与微分的求解 第三章 定理与导数的应用 3.1 微分中值定理 3.2 洛必达法则 3.3 泰勒公式 3.4 函数的单调性与凹凸性 3.5 函数的极值和最值 3.6 函数图形的描绘 3.7* 曲线的曲率 知识点: 1. 理解罗尔(Rolle)定理 2. 理解拉格朗日(Lagrange)定理 3. 了解柯西(Cauchy)定理 自学内容:微分中值定理 课堂作业: 1.微分中值定理的应用 2.洛必达法则的应用 3.函数图形的描绘、渐近线的求解 课外作业: 1.完成本章小结 2.应用微分中值定理求解实际问题 3.应用洛必达法则求导 4.求函数的单调性、凹凸性、极值和最值

4.掌握洛必达法则 5.理解函数的极值概念 6.掌握用导数判断函数的单调性和求极值 7.了解用导数判断函数图形的凹凸性 8.理解拐点的概念及求解 9.了解函数图形的描绘(渐近线) 10.会求筒单的最值应用问题 第四章不定积分 自学内容:不定积分的概念与性质 4.1不定积分的概念与性质 4.2换元积分法 课堂作业: 4.3分部积分法 1.直接积分法求不定积分 4.4有理函数的积分 2.换元积分法求不定积分 知识点: 3.分部积分法求不定积分 1.理解不定积分的概念与性质 2.掌握不定积分的换元法与分部积分法 课外作业: 3.会求几类简单有理函数的积分 1完成本章小结 2.不定积分的求解 第五章定积分 自学内容:定积分的概念与性质 5.1定积分的概念 5.2微积分基本公式 课堂作业: 5.3定积分的换元法和分部积分法 1.定义法求定积分 5.4反常积分 2.换元法求定积分 知识点: 3.分部积分法求定积分 1.理解定积分的概念与性质 4.反常积分的求解 2.掌握定积分的换元法与分部积分法 3.理解变上限积分函数的概念及求导 课外作业: 4.了解微积分基本定理 1.完成本章小结 5.了解反常积分的概念及筒单计算 2.定积分的求解 第六章定积分的应用 自学内容:微元法 6.1定积分的微元法 6.2定积分在几何上的应用 课堂作业: 6.3定积分在物理上的应用 1求平面图形的面积 知识点: 2.求体积 1.理解定积分的微元法 3.求平面曲线的弧长 2.掌握定积分在求平面图形面积 4.求变力沿直线运动的做功 3.了解定积分在求体积、弧长中的应用 4.了解定积分在物理上的应用(变力沿直线运 课外作业: 动做功) 1完成本章小结 2.定积分在几何和物理上的应用 第七章微分方程 自学内容:微分方程的基本概念 7.1微分方程的基本概念 7.2初等积分法 课堂作业: 7.3可降阶的高阶微分方程 1变量可分离方程的求解 7.4二阶常系数线性微分方程 2.一阶线性方程的求解 知识点: 3.齐次方程的求解
5 4. 掌握洛必达法则 5. 理解函数的极值概念 6. 掌握用导数判断函数的单调性和求极值 7. 了解用导数判断函数图形的凹凸性 8. 理解拐点的概念及求解 9. 了解函数图形的描绘(渐近线) 10. 会求简单的最值应用问题 第四章 不定积分 4.1 不定积分的概念与性质 4.2 换元积分法 4.3 分部积分法 4.4 有理函数的积分 知识点: 1. 理解不定积分的概念与性质 2. 掌握不定积分的换元法与分部积分法 3. 会求几类简单有理函数的积分 自学内容:不定积分的概念与性质 课堂作业: 1.直接积分法求不定积分 2.换元积分法求不定积分 3.分部积分法求不定积分 课外作业: 1.完成本章小结 2.不定积分的求解 第五章 定积分 5.1 定积分的概念 5.2 微积分基本公式 5.3 定积分的换元法和分部积分法 5.4 反常积分 知识点: 1. 理解定积分的概念与性质 2. 掌握定积分的换元法与分部积分法 3. 理解变上限积分函数的概念及求导 4. 了解微积分基本定理 5. 了解反常积分的概念及简单计算 自学内容:定积分的概念与性质 课堂作业: 1.定义法求定积分 2.换元法求定积分 3.分部积分法求定积分 4.反常积分的求解 课外作业: 1.完成本章小结 2.定积分的求解 第六章 定积分的应用 6.1 定积分的微元法 6.2 定积分在几何上的应用 6.3 定积分在物理上的应用 知识点: 1. 理解定积分的微元法 2. 掌握定积分在求平面图形面积 3. 了解定积分在求体积、弧长中的应用 4. 了解定积分在物理上的应用(变力沿直线运 动做功) 自学内容:微元法 课堂作业: 1.求平面图形的面积 2.求体积 3.求平面曲线的弧长 4.求变力沿直线运动的做功 课外作业: 1.完成本章小结 2.定积分在几何和物理上的应用 第七章 微分方程 7.1 微分方程的基本概念 7.2 初等积分法 7.3 可降阶的高阶微分方程 7.4 二阶常系数线性微分方程 知识点: 自学内容:微分方程的基本概念 课堂作业: 1.变量可分离方程的求解 2.一阶线性方程的求解 3.齐次方程的求解
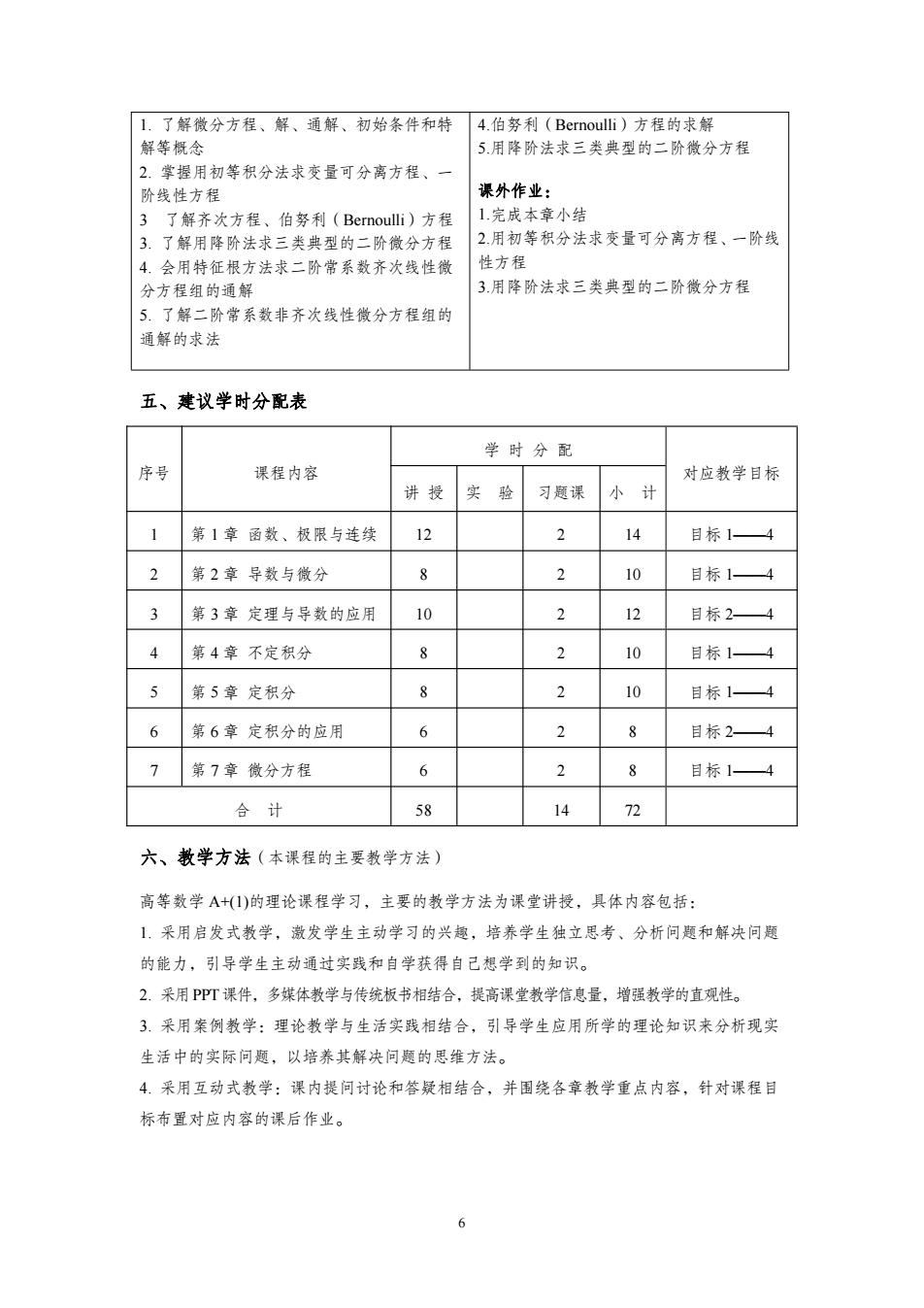
1.了解微分方程、解、通解、初始条件和特 4.伯努利(Bernoulli)方程的求解 解等概念 5.用降阶法求三类典型的二阶微分方程 2.掌握用初等积分法求变量可分离方程、一 阶线性方程 课外作业: 3了解齐次方程、伯努利(Bernoulli)方程 1完成本章小结 3.了解用降阶法求三类典型的二阶微分方程 2.用初等积分法求变量可分离方程、一阶线 4.会用特征根方法求二阶常系数齐次线性微 性方程 分方程组的通解 3.用降阶法求三类典型的二阶微分方程 5.了解二阶常系数非齐次线性微分方程组的 通解的求法 五、建议学时分配表 学时分配 序号 课程内容 对应教学目标 讲授 实验 习题课 小计 1 第1章函数、极限与连续 12 2 14 目标1一4 2 第2章导数与微分 8 2 10 目标1一4 3 第3章定理与导数的应用 10 2 12 目标2 4 第4章不定积分 8 2 10 目标 第5章定积分 8 2 10 目标 6 第6章定积分的应用 6 目标2 7 第7章微分方程 6 2 8 目标1一4 合计 58 14 72 六、教学方法(本课程的主要教学方法) 高等数学A+I)的理论课程学习,主要的教学方法为课堂讲授,具体内容包括: 1.采用启发式教学,激发学生主动学习的兴趣,培养学生独立思考、分析问题和解决问题 的能力,引导学生主动通过实践和自学获得自己想学到的知识。 2.采用PPT课件,多煤体教学与传统板书相结合,提高课堂教学信息量,增强教学的直观性。 3.采用案例教学:理论教学与生活实践相结合,引导学生应用所学的理论知识来分析现实 生活中的实际问题,以培养其解决问题的思维方法。 4.采用互动式教学:课内提问讨论和答疑相结合,并围绕各章教学重点内容,针对课程目 标布置对应内容的课后作业
6 1. 了解微分方程、解、通解、初始条件和特 解等概念 2. 掌握用初等积分法求变量可分离方程、一 阶线性方程 3 了解齐次方程、伯努利(Bernoulli)方程 3. 了解用降阶法求三类典型的二阶微分方程 4. 会用特征根方法求二阶常系数齐次线性微 分方程组的通解 5. 了解二阶常系数非齐次线性微分方程组的 通解的求法 4.伯努利(Bernoulli)方程的求解 5.用降阶法求三类典型的二阶微分方程 课外作业: 1.完成本章小结 2.用初等积分法求变量可分离方程、一阶线 性方程 3.用降阶法求三类典型的二阶微分方程 五、建议学时分配表 序号 课程内容 学 时 分 配 对应教学目标 讲 授 实 验 习题课 小 计 1 第 1 章 函数、极限与连续 12 2 14 目标 1——4 2 第 2 章 导数与微分 8 2 10 目标 1——4 3 第 3 章 定理与导数的应用 10 2 12 目标 2——4 4 第 4 章 不定积分 8 2 10 目标 1——4 5 第 5 章 定积分 8 2 10 目标 1——4 6 第 6 章 定积分的应用 6 2 8 目标 2——4 7 第 7 章 微分方程 6 2 8 目标 1——4 合 计 58 14 72 六、教学方法(本课程的主要教学方法) 高等数学 A+(1)的理论课程学习,主要的教学方法为课堂讲授,具体内容包括: 1. 采用启发式教学,激发学生主动学习的兴趣,培养学生独立思考、分析问题和解决问题 的能力,引导学生主动通过实践和自学获得自己想学到的知识。 2. 采用PPT课件,多媒体教学与传统板书相结合,提高课堂教学信息量,增强教学的直观性。 3. 采用案例教学:理论教学与生活实践相结合,引导学生应用所学的理论知识来分析现实 生活中的实际问题,以培养其解决问题的思维方法。 4. 采用互动式教学:课内提问讨论和答疑相结合,并围绕各章教学重点内容,针对课程目 标布置对应内容的课后作业
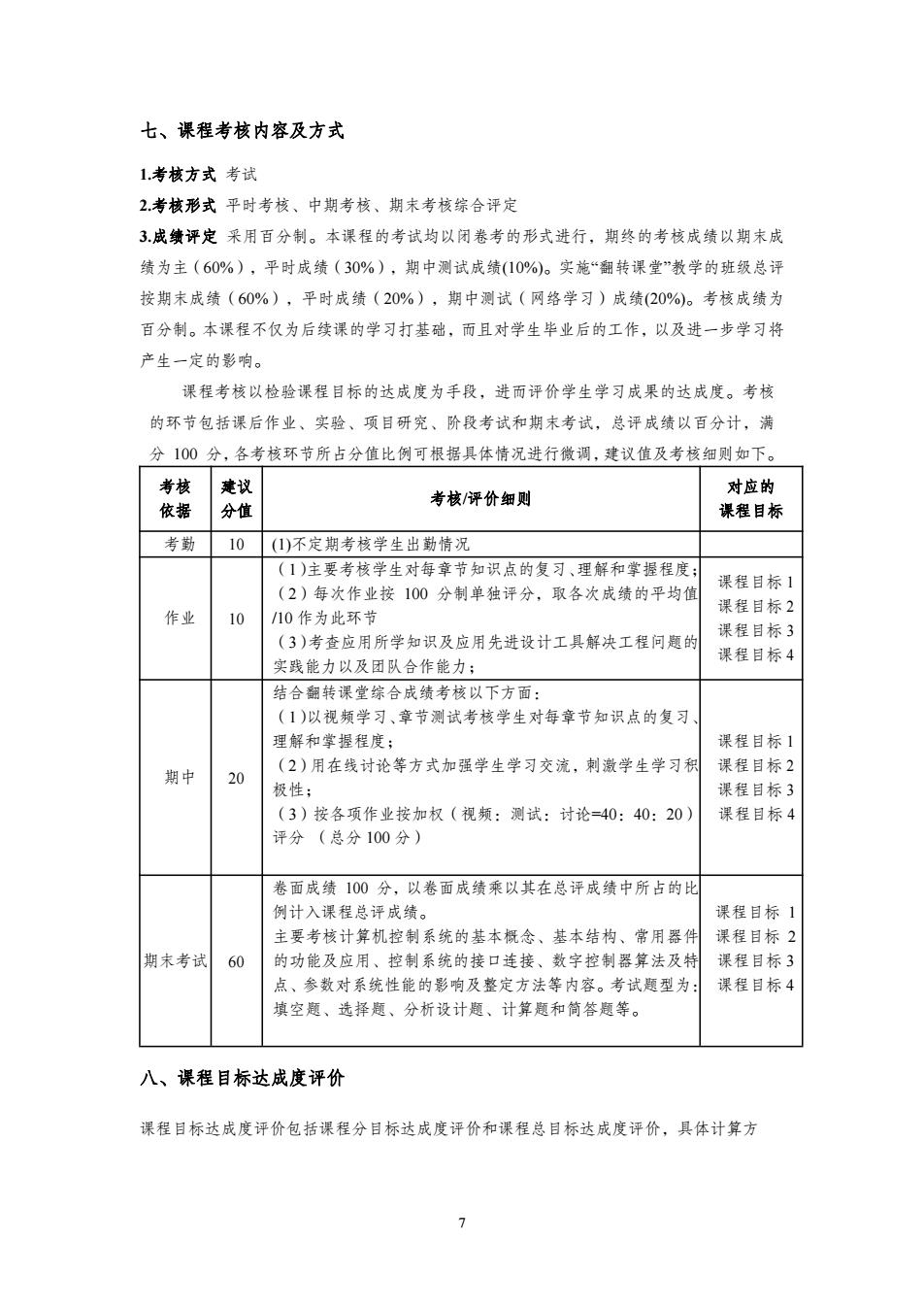
七、课程考核内容及方式 1考核方式考试 2考核形式平时考核、中期考核、期末考核综合评定 3成绩评定采用百分制。本课程的考试均以闭卷考的形式进行,期终的考核成绩以期末成 绩为主(60%),平时成绩(30%),期中测试成绩(10%)。实施“翻转课堂”教学的班级总评 按期末成绩(60%),平时成绩(20%),期中测试(网络学习)成绩(20%)。考核成绩为 百分制。本课程不仅为后续课的学习打基础,而且对学生毕业后的工作,以及进一步学习将 产生一定的影响。 课程考核以检验课程目标的达成度为手段,进而评价学生学习成果的达成度。考核 的环节包括课后作业、实验、项目研究、阶段考试和期末考试,总评成绩以百分计,满 分100分,各考核环节所占分值比例可根据具体情况进行微调,建议值及考核细则如下。 考核 建议 对应的 依据 分值 考核/评价细则 课程目标 考勤 10 (1)不定期考核学生出勤情况 (1)主要考核学生对每章节知识点的复习、理解和掌握程度; (2)每次作业按100分制单独评分,取各次成绩的平均值 课程目标1 课程目标2 作业 10 /10作为此环节 课程目标3 (3)考查应用所学知识及应用先进设计工具解决工程问题的 课程目标4 实践能力以及团队合作能力; 结合翻转课堂综合成绩考核以下方面: (1)以视频学习、章节测试考核学生对每章节知识点的复习 理解和掌握程度; 课程目标1 期中 (2)用在线讨论等方式加强学生学习交流,刺激学生学习积 课程目标2 20 极性; 课程目标3 (3)按各项作业按加权(视频:测试:讨论=40:40:20) 课程目标4 评分(总分100分) 卷面成绩100分,以卷面成绩乘以其在总评成绩中所占的比 例计入课程总评成绩。 课程目标1 主要考核计算机控制系统的基本概念、基本结构、常用器件 课程目标2 期末考试 60 的功能及应用、控制系统的接口连接、数字控制器算法及特 课程目标3 点、参数对系统性能的影响及整定方法等内容。考试題型为: 课程目标4 填空题、选择题、分析设计题、计算题和简答题等。 八、课程目标达成度评价 课程目标达成度评价包括课程分目标达成度评价和课程总目标达成度评价,具体计算方 >
7 七、课程考核内容及方式 1.考核方式 考试 2.考核形式 平时考核、中期考核、期末考核综合评定 3.成绩评定 采用百分制。本课程的考试均以闭卷考的形式进行,期终的考核成绩以期末成 绩为主(60%),平时成绩(30%),期中测试成绩(10%)。实施“翻转课堂”教学的班级总评 按期末成绩(60%),平时成绩(20%),期中测试(网络学习)成绩(20%)。考核成绩为 百分制。本课程不仅为后续课的学习打基础,而且对学生毕业后的工作,以及进一步学习将 产生一定的影响。 课程考核以检验课程目标的达成度为手段,进而评价学生学习成果的达成度。考核 的环节包括课后作业、实验、项目研究、阶段考试和期末考试,总评成绩以百分计,满 分 100 分,各考核环节所占分值比例可根据具体情况进行微调,建议值及考核细则如下。 考核 依据 建议 分值 考核/评价细则 对应的 课程目标 考勤 10 (1)不定期考核学生出勤情况 作业 10 (1)主要考核学生对每章节知识点的复习、理解和掌握程度; (2)每次作业按 100 分制单独评分,取各次成绩的平均值 /10 作为此环节 (3)考查应用所学知识及应用先进设计工具解决工程问题的 实践能力以及团队合作能力; 课程目标 1 课程目标 2 课程目标 3 课程目标 4 期中 20 结合翻转课堂综合成绩考核以下方面: (1)以视频学习、章节测试考核学生对每章节知识点的复习、 理解和掌握程度; (2)用在线讨论等方式加强学生学习交流,刺激学生学习积 极性; (3)按各项作业按加权(视频:测试:讨论=40:40:20) 评分 (总分 100 分) 课程目标 1 课程目标 2 课程目标 3 课程目标 4 期末考试 60 卷面成绩 100 分,以卷面成绩乘以其在总评成绩中所占的比 例计入课程总评成绩。 主要考核计算机控制系统的基本概念、基本结构、常用器件 的功能及应用、控制系统的接口连接、数字控制器算法及特 点、参数对系统性能的影响及整定方法等内容。考试题型为: 填空题、选择题、分析设计题、计算题和简答题等。 课程目标 1 课程目标 2 课程目标 3 课程目标 4 八、课程目标达成度评价 课程目标达成度评价包括课程分目标达成度评价和课程总目标达成度评价,具体计算方