
细台形2幸院 antai Institute of Technology 原城台好火维年馆 第4章机器人的逆向运动学 四4.1导读 四4.2求解概念 四4.3多重解 四4.4求解方法 四4.5三角函数方程的求解 四4.6 Piper解 2
2 4.1 导读 4.2 求解概念 4.3 多重解 4.4 求解方法 4.5 三角函数方程的求解 4.6 Piper解 第4章 机器人的逆向运动学
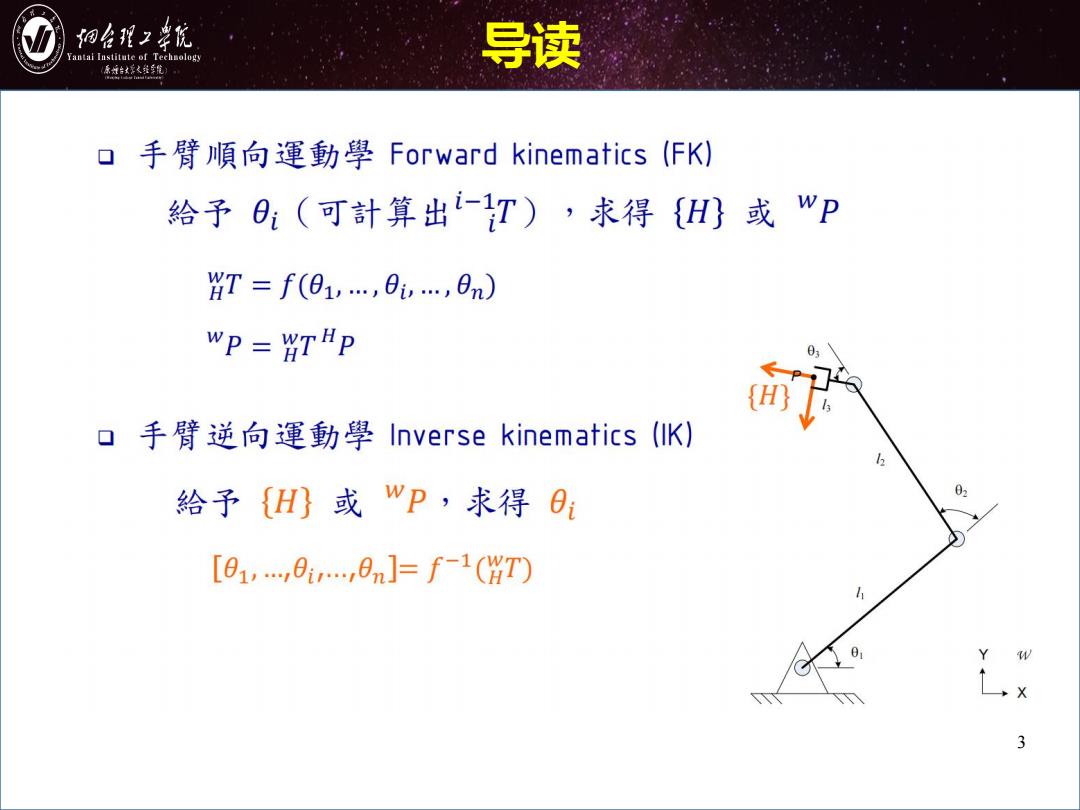
细台程2幸统 antai Institute of Technology 导读 原城台好火维年航 口手臂順向運動學Forward kinematics(FK) 給予O:(可計算出iT),求得H)或wP HT=f(01,…,0i,…,0m) WP -WTHP H o手臂逆向運動學Inverse kinematics(lK) 給予{H或wP,求得O 02 [01,…,0…,0n]=f-1(wT) 3
3 导读
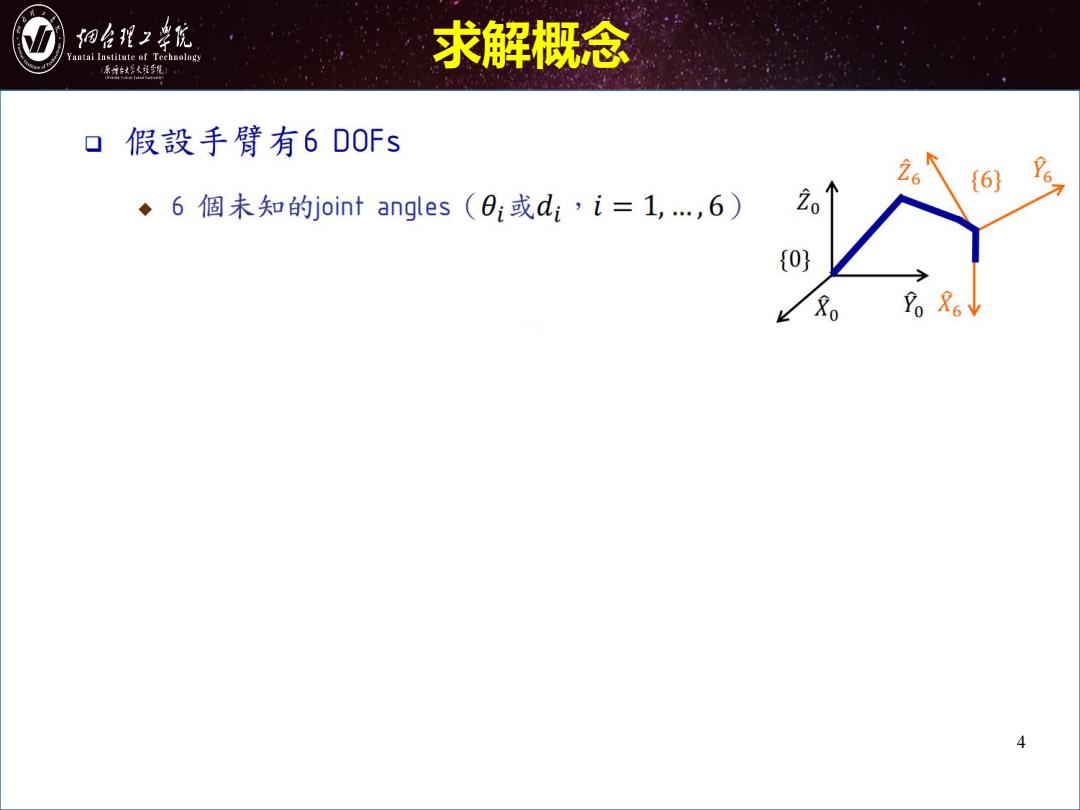
细台形z幸院 antai Institute of Technology 求解概念 原城台好火维年院 ▣假設手臂有6D0Fs 26 {6 ◆6個未知的joint angles(0:或d;,i=1,…,6) 20 0} 4
4 求解概念
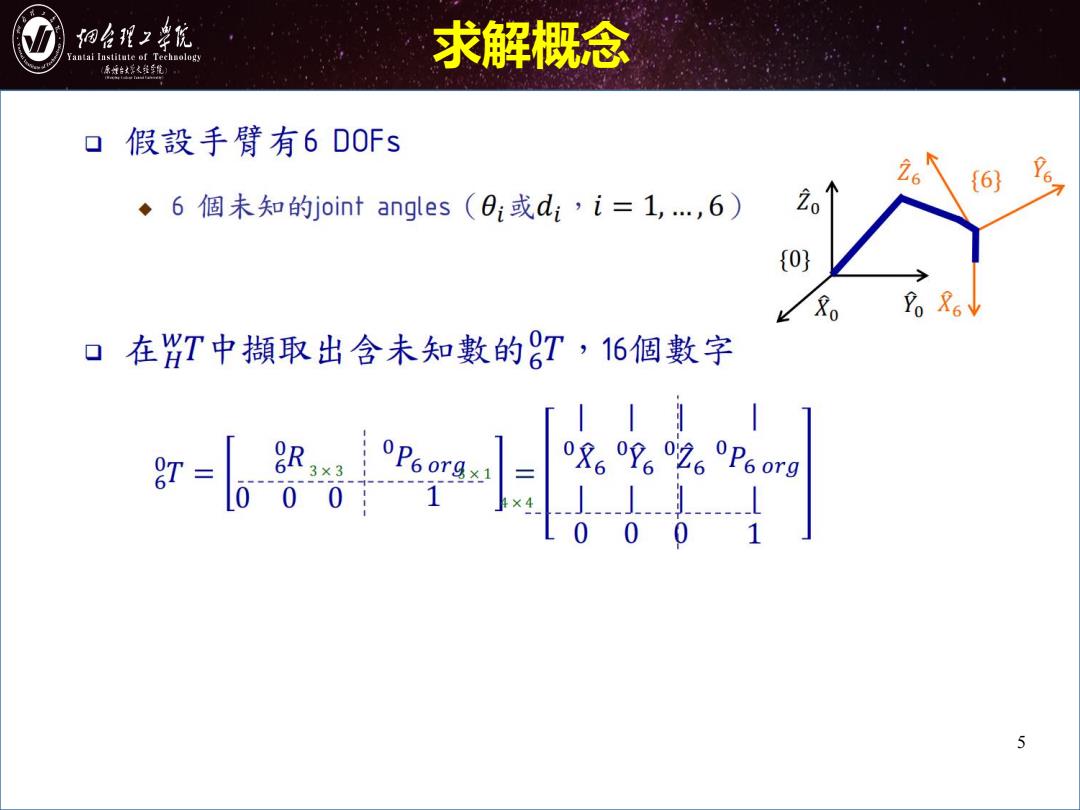
细台形2幸院 antai Institute of Technology 求解概念 原城台好火维年馆 ▣假設手臂有6D0Fs 26 {6 Y6 ◆6個未知的joint angles(0:或d;,i=1,,6) 20 {0} 口在HT中擷取出含未知數的T,16個數字 r= 08.2.26P6rg 5
5 求解概念
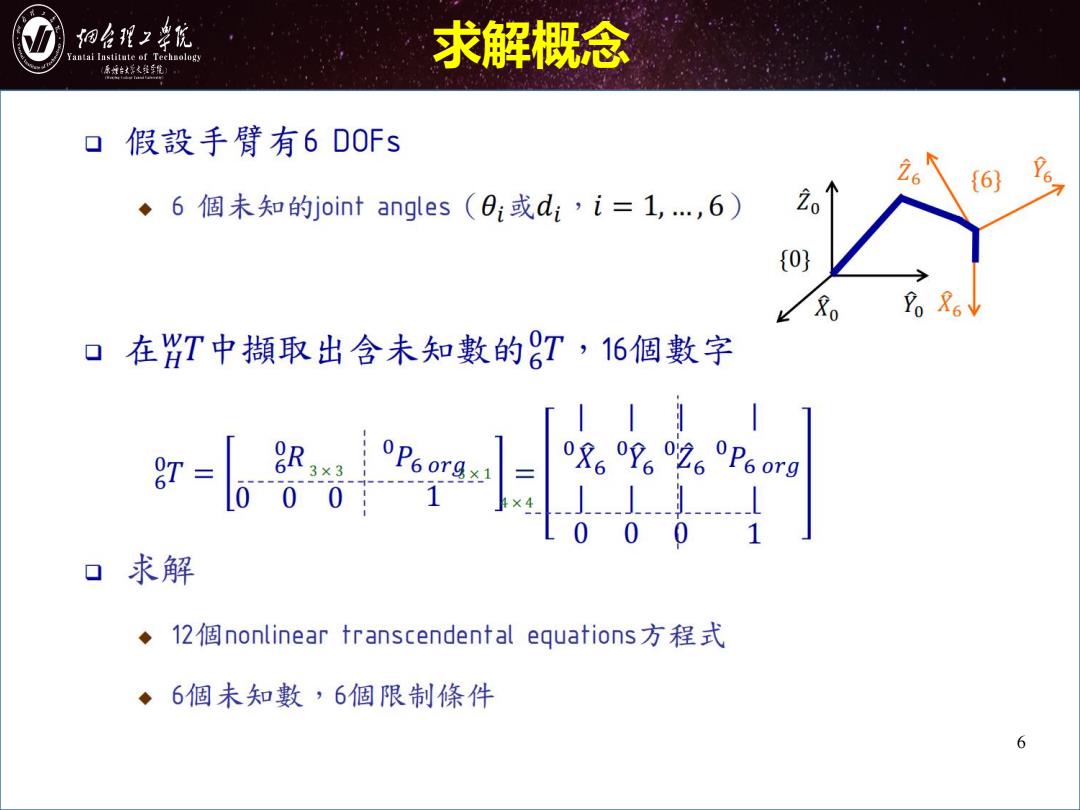
阳台现2华航 antai Institute of Technology 求解概念 原城台文之维单能 ▣假設手臂有6D0Fs 26 {6] ◆6個未知的joint angles(0:或d;’i=1,,6) 20 {0} Po &6 口在YT中擷取出含未知數的T,16個數字 r= 8..26P6rg 0 )01 口求解 ◆12個nonlinear transcendental equations方程式 ◆6個未知數,6個限制條件 6
6 求解概念

细台形z幸院 antai Institute of Technology 求解概念 原城台好火维年院 Reachable workspace ◆手臂可以用一種以上的姿態到達的位置 7
7 求解概念

细台形z幸院 antai Institute of Technology 求解概念 原城台好火维年院 Reachable workspace ◆手臂可以用一種以上的姿態到達的位置 Dexterous workspace ◆手臂可以用任何的姿態到達的位置 8
8 求解概念

阳台程2幸优 Yantai Institute of Technology 求解概念 原城台好火维年院 Reachable workspace ◆手臂可以用一種以上的姿態到達的位置 口Dexterous workspace ◆手臂可以用任何的姿態到達的位置 Ex:A RR manipulator If l l2 Reachable workspace 9
9 求解概念

阳台程2幸优 antai Institute of Technology 求解概念 原城台好火维年能 Reachable workspace ◆手臂可以用一種以上的姿態到達的位置 口Dexterous workspace ·手臂可以用任何的姿態到達的位置 Ex:A RR manipulator If l l2 If l l2 Reachable workspace Dexterous workspace 10
10 求解概念
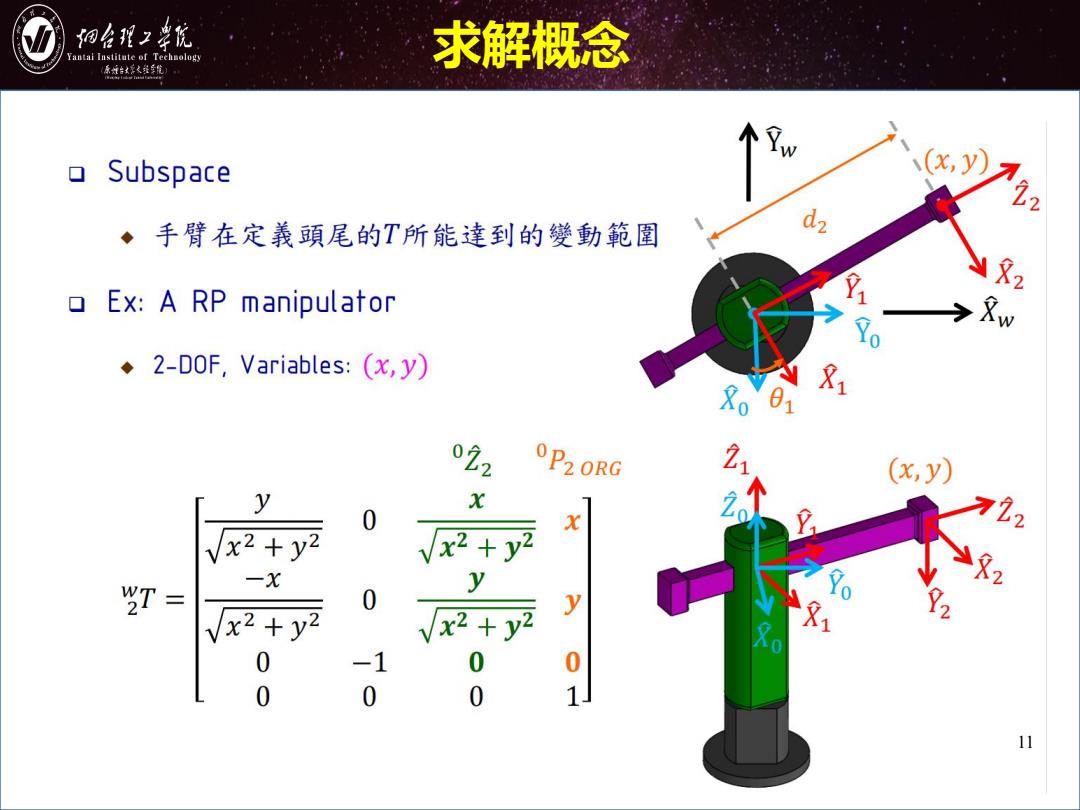
细台程2幸优 Yantai Institute of Technology 求解概念 原城台好火维年馆 Subspace ◆手臂在定義頭尾的T所能達到的變動範圍 Ex:A RP manipulator Xw 2-DOF,Variables:(x,y) 8001 81 0P2ORG (x,y) y X 0 X 22 x2+y2 √x2 y2 X2 WT= 0 Vx2+y2 vx2 y2 y 00 -1 0 0 0 0 1」 11
11 求解概念